LeetCode704.二分查找及二分法
每日一题:LeetCode704.二分查找
- LeetCode704.二分查找
- 知识点:二分法
- 解题
- 代码
LeetCode704.二分查找
问题描述:给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
知识点:二分法
-
定义:二分查找算法也称折半搜索算法,对数搜索算法,是一种在有序数组中查找某一特定元素的搜索算法。搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半,时间复杂度是log(n)
- 一是有序数组(这里可能是整体有序比如[1,2,3,4,5],也有可能是局部有序比如[4,5,1,2,3]),
- 二是特定元素(也有可能是满足特定的条件)。由定义我们大概就知道了二分法的应用场景,在有序数组中找特定值都可以考虑用二分法
-
二分法的步骤
我们要在一组升序的数组找一个数的下标,那我们肯定是先拿中间的与他进行比较,比较大小的判断,其实就相当于是这个性质,且这个 性质满足二段性,将大于和小于我们要查找的值分为两段,而我们的查找结果就是分界点 -
二分法的使用条件:①上下界确定 ②区间内有序(也可以是局部有序)
解题
思路:①这道题目的前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件②二分查找涉及的很多的边界条件,逻辑比较简单,但就是写不好。例如到底是 while(left < right) 还是 while(left <= right),到底是right = middle呢,还是要right = middle - 1呢?③写二分法,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
-
第一种写法,定义 target 是在一个在左闭右闭的区间里,也就是[left, right] (这个很重要非常重要)。
区间的定义这就决定了二分法的代码应该如何写,因为定义target在[left, right]区间,所以有如下两点:- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:
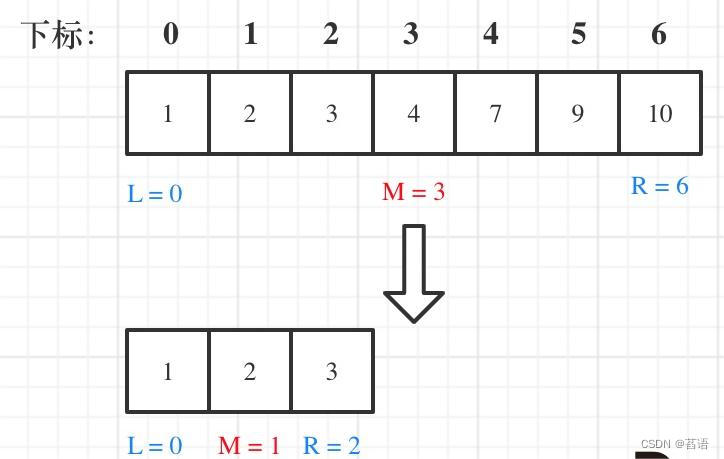
-
第二种方法
如果说定义 target 是在一个在左闭右开的区间里,也就是[left, right) ,那么二分法的边界处理方式则截然不同。
有如下两点:- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(注意和方法一的区别)
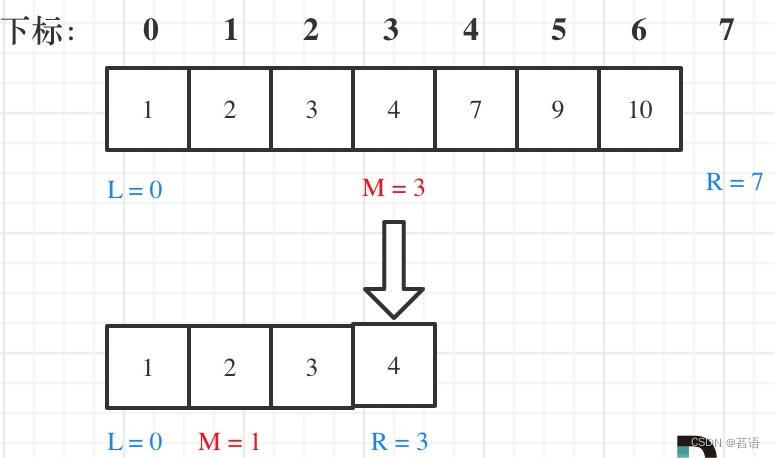
代码
python:(版本一)左闭右闭区间
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) - 1 # 定义target在左闭右闭的区间里,[left, right]while left <= right:mid = (left + right)/2if nums[middle] > target:right = middle - 1 # target在左区间,所以[left, middle - 1]elif nums[middle] < target:left = middle + 1 # target在右区间,所以[middle + 1, right]else:return middle # 数组中找到目标值,直接返回下标return -1 # 未找到目标值
python:(版本二)左闭右开区间
class Solution:def search(self, nums: List[int], target: int) -> int:left, right = 0, len(nums) # 定义target在左闭右开的区间里,即:[left, right)while left < right: # 因为left == right的时候,在[left, right)是无效的空间,所以使用 <mid = (left + right)/2if nums[middle] > target:right = middle # target 在左区间,在[left, middle)中elif nums[middle] < target:left = middle + 1 # target 在右区间,在[middle + 1, right)中else:return middle # 数组中找到目标值,直接返回下标return -1 # 未找到目标值
C++:(版本一)左闭右闭区间
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=int middle = (left + right)/2;// 防止溢出 等同于(left + right)/2if (nums[middle] > target) {right = middle - 1; // target 在左区间,所以[left, middle - 1]} else if (nums[middle] < target) {left = middle + 1; // target 在右区间,所以[middle + 1, right]} else { // nums[middle] == targetreturn middle; // 数组中找到目标值,直接返回下标}}// 未找到目标值return -1;}
};
C++:(版本二)左闭右开区间
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <int middle = (left + right)/2;if (nums[middle] > target) {right = middle; // target 在左区间,在[left, middle)中} else if (nums[middle] < target) {left = middle + 1; // target 在右区间,在[middle + 1, right)中} else { // nums[middle] == targetreturn middle; // 数组中找到目标值,直接返回下标}}// 未找到目标值return -1;}
};
相关文章:

LeetCode704.二分查找及二分法
每日一题:LeetCode704.二分查找 LeetCode704.二分查找知识点:二分法解题代码 LeetCode704.二分查找 问题描述:给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中…...
2023年R1快开门式压力容器操作证模拟考试题库及R1快开门式压力容器操作理论考试试题
题库来源:安全生产模拟考试一点通公众号小程序 2023年R1快开门式压力容器操作证模拟考试题库及R1快开门式压力容器操作理论考试试题是由安全生产模拟考试一点通提供,R1快开门式压力容器操作证模拟考试题库是根据R1快开门式压力容器操作最新版教材&#…...

探索NLP中的核心架构:编码器与解码器的区别
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️ 👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
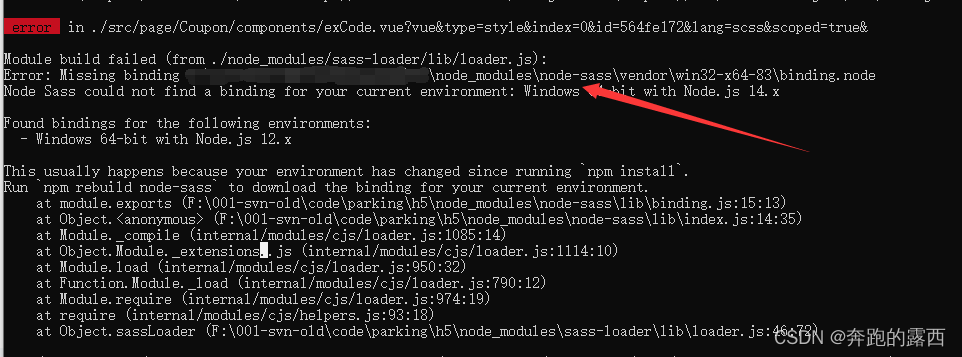
解决:Error: Missing binding xxxxx\node_modules\node-sass\vendor\win32-x64-83\
一、具体报错 二、报错原因 这个错误是由于缺少 node-sass 模块的绑定文件引起的。 三、导致原因 3.1、环境发生了变化 3.2、安装过程出现问题 四、解决方法步骤: 4.1、重新构建 node-sass 模块 npm rebuild node-sass 4.2、清除缓存并重新安装依赖 npm c…...

科研学习|科研软件——面板数据、截面数据、时间序列数据的区别是什么?
一、数据采集方式不同 面板数据是通过在多个时间点上对同一组体进行观测而获得的数据。面板数据可以是横向面板数据,即对同一时间点上不同个体的观测,也可以是纵向面板数据,即对同一个体在不同时间点上的观测。采集面板数据需要跟踪相同的个体…...

【UE5】物体沿样条线移动
目录 效果 步骤 一、使用样条线创建路径 二、创建沿样条线路径移动的物体 三、定义可移动物体的生成器 效果 步骤 一、使用样条线创建路径 先创建一个Actor蓝图,这里命名为“BP_Line” 该蓝图中只需添加一个样条组件 将“BP_Line”拖入场景中 按住Alt鼠标左键…...
Qt控件按钮大全
按钮 在 Qt 里,最常用使用的控件就是按钮了,有了按钮,我们就可以点击,从而响应事件,达到人机交互的效果。不管是嵌入式或者 PC 端,界面交互,少不了按钮。Qt 按钮部件是一种常用的部件之一,Qt 内置了六种按钮部件如下: (1) QPushButton:下压按钮 (2) QToolBu…...
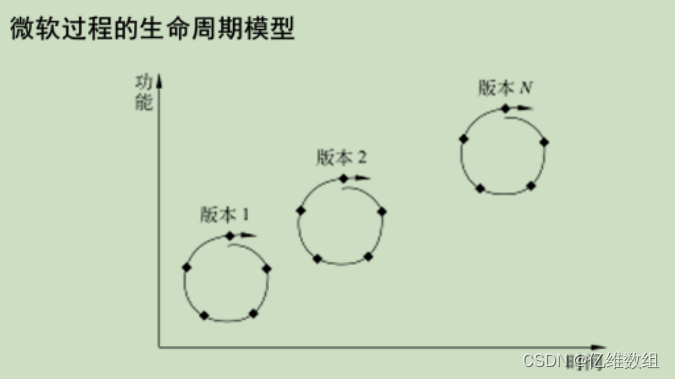
软件工程--软件过程学习笔记
本篇内容是对学校软件工程课堂内容的记录总结,部分也来源于网上查找的资料 软件过程基础 软件过程是指在软件开发过程中,经过一系列有序的步骤和活动,从问题定义到最终软件产品交付和维护的全过程。这个过程旨在确保软件项目能够按时、按预…...
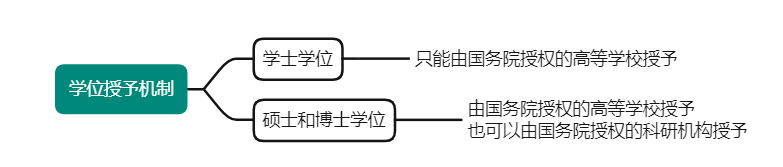
高校教师资格证备考
高等教育制度 关于人的全面发展和个体发展的关系,说法正确的是(ABC)。 A.个体发展是在全面发展基础上的选择性发展 B.全面发展是个体发展的前提和基础 C.个体发展又是全面发展的动力 D.个体发展是全面发展的前提和基础...

Git通过rebase合并多个commit
在使用 Git 作为版本控制的时候,我们可能会由于各种各样的原因提交了许多临时的 commit,而这些 commit 拼接起来才是完整的任务。那么我们为了避免太多的 commit 而造成版本控制的混乱,通常我们推荐将这些 commit 合并成一个。 1. 查看提交历…...
ROS 学习应用篇(八)ROS中的坐标变换管理之tf广播与监听的编程实现
偶吼吼胜利在望,冲冲冲 老规矩新建功能包 工作空间目录下/src下开启终端输入 catkin_create_pkg learning_tf roscpp rospy tf turtlesim 如何实现tf广播 引入库 c python …...

计算机算法分析与设计(23)---二分搜索算法(C++)
文章目录 1. 算法介绍2. 代码编写 1. 算法介绍 1. 二分搜索(英语:binary search),也称折半搜索(英语:half-interval search)、对数搜索(英语:logarithmic search…...
前置语音群呼与语音机器人群呼哪个更好
最近通过观察自己接到的营销电话,通过语音机器人外呼的量应该有所下降。同时和客户交流获取到的信息,也是和这个情况类似,很多AI机器人群呼的量转向了OKCC前置语音群呼。询问原因,说是前置语音群呼转化更快,AI机器人群…...

『Element Plus の 百科大全』
Element Plus 官网 点击跳转...

P3879 [TJOI2010] 阅读理解- 字典树
题面 分析 将所有单词存入字典树,重点值怎么判断在哪一行出现过,对于字典树查询的判断字符串是否存在的数组可以开成二维,也就是在查询到某个字符串存在后,再通过循环判断每一层是否存在。 代码 #include <bits/stdc.h>…...
)
upgrade k8s (by quqi99)
作者:张华 发表于:2023-11-17 版权声明:可以任意转载,转载时请务必以超链接形式标明文章原始出处和作者信息及本版权声明(http://blog.csdn.net/quqi99) 本文只是从网上搜索一些升级k8s的理论学习,下面的步骤未实际测…...
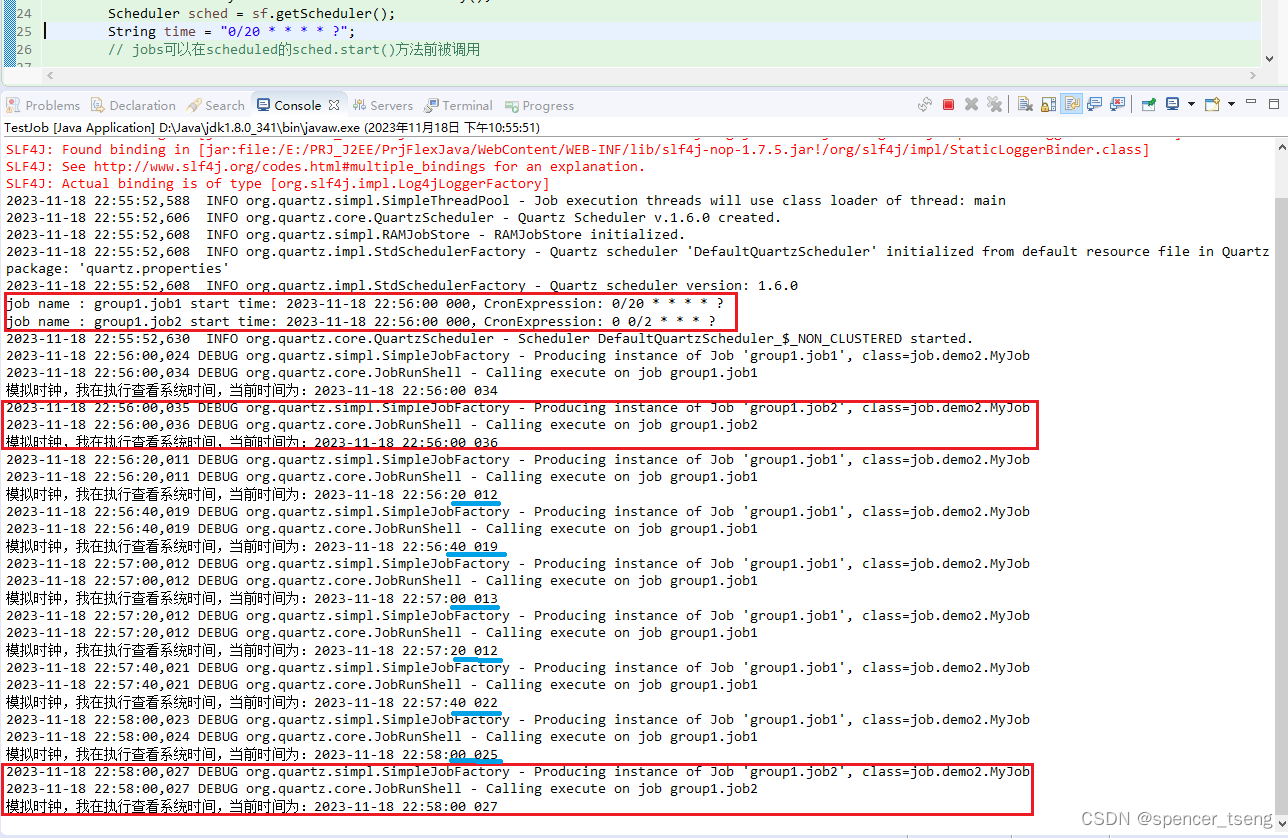
CronExpression
CronTrigger配置格式: 格式: [秒] [分] [小时] [日] [月] [周] [年]序号 说明 是否必填 允许填写的值 允许的通配符 1 秒 是 0-59 , - * / 2 分 是 0-59 , - * / 3 小时 是 0-23 , - * / 4 日 是 1-31 , - * ? / L W 5 月 是 1-12 or JA…...

释放机器人潜力,INDEMIND深耕底层技术
市场转暖,但攘外需要同时安内。 市场降温之后,正迎来拐点 疫情之后,经济逐渐下行,服务机器人的“好日子”也随之结束,整个行业都在动荡中经历渡劫。根据TE智库报告显示,从2022年开始,我国服务…...

【ES6标准入门】JavaScript中的模块Module语法的使用细节:export命令和imprt命令详细使用,超级详细!!!
😁 作者简介:一名大四的学生,致力学习前端开发技术 ⭐️个人主页:夜宵饽饽的主页 ❔ 系列专栏:JavaScript进阶指南 👐学习格言:成功不是终点,失败也并非末日,最重要的是继…...

流量2----2
2...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
