【笔记 Pytorch】稀疏矩阵、scipy.sparse模块的使用
安装:pip install scipy
描述:就是专门为了解决稀疏矩阵而生。导入模块:from scipy import sparse
优缺点总结
| 七种矩阵类型 | 描述 |
|---|---|
| coo_matrix ★ | 【名称】coordinate format 【优点】 ① 不同稀疏格式间转换效率高(特别是CSR和CSC) ② 不支持元素的存取和增删,但是易于保存和读取。 ③ 构建矩阵时,允许坐标重复。 【缺点】 ① 不能直接运算; ② 不能直接切片操作。 |
| dok_matrix | 【说明】基于Keys的稀疏矩阵字典. (Dictionary of Keys format) 【功能】创建、转换 |
| lil_matrix ★ | 【名称】基于行的链表稀疏矩阵 (List of Lists format) 【优点】 ① 快速按行切片 ② 高效地添加、删除、查找元素 【缺点】 ① 按列切片很慢(建议CSC) ② 算术运算LIL+LIL很慢(考虑CSR或CSC) |
| csr_matrix | 【名称】Compressed Sparse Row format 【优点】 ① 高效的矩阵加法与乘法内积运算 ② 高效的行切片操作 ③ CSR格式在存储稀疏矩阵时非零元素平均使用的字节数(Bytes per Nonzero Entry)最为稳定(float类型约为8.5,double类型约为12.5)CSR格式常用于读入数据后进行稀疏矩阵计算。 【缺点】 ① 列切片操作慢(相比CSC) ② 转换成稀疏结构成本高(相比LIL) |
| csc_matrix | 【名称】Compressed Sparse Column format 【优点】 ① 高效的矩阵加法与乘法内积运算 ② 高效的列切片操作 【缺点】 ① 矩阵内积操作没有CSR快 ② 行切片操作慢(相比CSR) ③ 转换成稀疏结构成本高(相比LIL) |
| bsr_matrix | 【名称】Block Sparse Row format |
| dia_matrix | 【名称】DIAgonal format |
使用总结
coo_matrix
创建
# 方式一:ijv 创建
>>> data = [5,2,3,0]
>>> row = [2,2,3,2]
>>> col = [3,4,2,3]
>>> c = sparse.coo_matrix((data,(row,col)),shape=(5,6))
>>> print(c.toarray())
[[0 0 0 0 0 0][0 0 0 0 0 0][0 0 0 5 2 0][0 0 3 0 0 0][0 0 0 0 0 0]]# 方式二:创建零矩阵
>>> from scipy.sparse import coo_matrix
>>> coo_matrix((3, 4), dtype=np.int8).toarray()
array([[0, 0, 0, 0],[0, 0, 0, 0],[0, 0, 0, 0]], dtype=int8)# 方式三:创建有重复索引的矩阵
>>> row = np.array([0, 0, 1, 3, 1, 0, 0])
>>> col = np.array([0, 2, 1, 3, 1, 0, 0])
>>> data = np.array([1, 1, 1, 1, 1, 1, 1])
>>> coo = coo_matrix((data, (row, col)), shape=(4, 4))
# Duplicate indices are maintained until implicitly or explicitly summed
>>> np.max(coo.data)
1
>>> coo.toarray()
array([[3, 0, 1, 0],[0, 2, 0, 0],[0, 0, 0, 0],[0, 0, 0, 1]])
【预处理】
# 整个过程是为了创建对称矩阵
# coo.T.multiply(coo.T > coo):找出不对称的正元素,并转置
# -coo.multiply(coo.T > coo):找出不对称的负元素,并将其删掉
coo = coo + coo.T.multiply(coo.T > coo) - coo.multiply(coo.T > coo)
【保存和读取】
import scipy.sparse as sparse
sparse.save_npz("coo_matrix.npz",coo_save)
coo=sparse.load_npz("coo_matrix.npz")
【转换】
# 转化为其他格式
>>> coo.tocsc()
>>> coo.tocsr()
>>> coo.todense() # 转化为 numpy.matrix类型
【转置】
# 转置
coo.T
dok_matrix
创建
# 创建
>>> import numpy as np
>>> from scipy.sparse import dok_matrix
>>> S = dok_matrix((5, 5), dtype=np.float32)
>>> for i in range(5):for j in range(5):S[i, j] = i + j
获取索引
from scipy.sparse import dok_matrix
S=dok_matrix((10,10),dtype=int)
S[1,1]=10
S[1,2]=10
S[1,3]=10
S[1,8]=10
tmp=(S[1,:]==10)
print(tmp.indices)
>>>[1 2 3 8]
转换
# convert to coo
S.tocoo()# convert to numpy
print(S.toarray())
>>>
[[ 0. 1. 2. 3. 4.][ 1. 2. 3. 4. 5.][ 2. 3. 4. 5. 6.][ 3. 4. 5. 6. 7.][ 4. 5. 6. 7. 8.]]
lil_matrix
【适用的场景】逐渐添加矩阵的元素。
【使用】
from scipy.sparse import lil_matrix
l = lil_matrix((6,5))
l[2,3] = 1
l[3,4] = 2
l[3,2] = 3
print(l.toarray())
>>>
[[ 0. 0. 0. 0. 0.][ 0. 0. 0. 0. 0.][ 0. 0. 0. 1. 0.][ 0. 0. 3. 0. 2.][ 0. 0. 0. 0. 0.][ 0. 0. 0. 0. 0.]]# 列求和
print(l.sum(0))
>>> [[0. 0. 3. 1. 2.]]# 行求和
print(l.sum(1))
>>>
[[0.][0.][1.][5.][0.][0.]]
dia_matrix
【使用】
>>> #data定义对角线元素,在这里是[1,2,3,4]。
>>> data = np.array([[1, 2, 3, 4]]).repeat(3, axis=0)
>>> #offsets定义对角线的偏移量,0代表正对角线,正数代表往上偏移,负数代表往下偏移
>>> offsets = np.array([0, -1, 2])
>>> dia_matrix((data, offsets), shape=(4, 4)).toarray()
array([[1, 0, 3, 0],[1, 2, 0, 4],[0, 2, 3, 0],[0, 0, 3, 4]])
csr_matrix
【使用】
>>> from scipy.sparse import csr_matrix
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],[0, 0, 3],[4, 5, 6]])
import numpy as np
from scipy.sparse import csr_matrix
arr = np.array([0, 0, 0, 0, 0, 1, 1, 0, 2])# 【创建压缩稀疏行】
print(csr_matrix(arr))(0, 5) 1 (0, 6) 1 (0, 8) 2 #【查看存储的不含0元素的数据】print(csr_matrix(arr).data)#【计算非0元素的总数】print(csr_matrix(arr).count_nonzero()) #【 删除矩阵中0元素】mat = csr_matrix(arr)mat.eliminate_zeros()#【删除重复项】mat = csr_matrix(arr)mat.sum_duplicates()#【行压缩(csr)转为列压缩(csc)】newarr = csr_matrix(arr).tocsc()
csc_matrix
【说明】压缩稀疏列矩阵(Compressed sparse column matrix)
【使用】
bsr_matrix
【使用】
BSR矩阵中的inptr列表的第i个元素与i+1个元素是储存第i行的数据的列索引以及数据的区间索引,即indices[indptr[i]:indptr[i+1]]为第i行元素的列索引,data[indptr[i]: indptr[i+1]]为第i行元素的data。在下面的例子中,对于第0行,indptr[0]:indptr[1] -> 0:2, 因此第0行的列为indice[0:2]=[0,2],data为data[0:2]=array([[[1, 1],[1, 1]],[[2, 2],[2, 2]]]),对应的就是最后结果的第0,1行.
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6]).repeat(4).reshape(6, 2, 2)
>>> bsr_matrix((data,indices,indptr), shape=(6, 6)).toarray()
array([[1, 1, 0, 0, 2, 2],[1, 1, 0, 0, 2, 2],[0, 0, 0, 0, 3, 3],[0, 0, 0, 0, 3, 3],[4, 4, 5, 5, 6, 6],[4, 4, 5, 5, 6, 6]])
相关文章:

【笔记 Pytorch】稀疏矩阵、scipy.sparse模块的使用
安装:pip install scipy 描述:就是专门为了解决稀疏矩阵而生。导入模块:from scipy import sparse 优缺点总结 七种矩阵类型描述coo_matrix ★【名称】coordinate format 【优点】 ① 不同稀疏格式间转换效率高(特别是CSR和CSC) …...

C#学习相关系列之Linq常用方法---排序(一)
一、构建数据 public class Student_1{public int ID { get; set; }public string Name { get; set; }public int Chinese { get; set; }public int Math { get; set; }public int English { get; set; }public override string ToString(){return string.Format("ID:{0},…...

Android Proguard混淆
关于作者:CSDN内容合伙人、技术专家, 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、人工智能等,希望大家多多支持。 目录 一、导读二、概览三、语法规则3.1 输入/输出选项3.2 保留选项3.3 缩…...
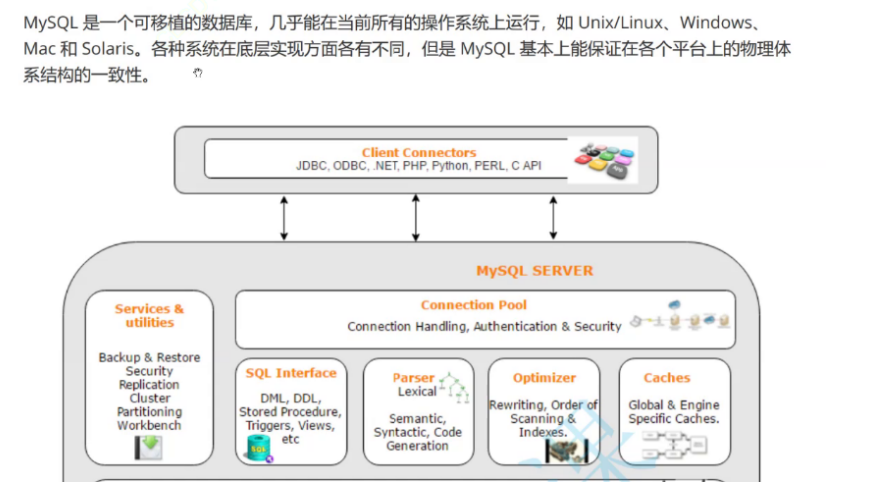
MySQL 1、初识数据库
一、什么是数据库? 以特定的格式保存好的文件,我们就叫做数据库。 提供较为便捷的数据的存取服务的软件集合、解决方案,我们就叫它数据库。 存储数据用文件就可以了,为什么还要弄个数据库。 文件或数据库都可以存储数据&#…...

H5ke11--3介绍本地,会话存储
代码顺序: 1.设置input,捕获input如果有多个用属性选择符例如 input[typefile]点击事件.向我们的本地存储设置键值对 2.在点击事件外面设置本地存储表示初始化的值.点击上面的事件才能修改我们想修改的值 会话(session)浏览a数据可以写到本地硬盘,关闭页面数据就没了 本地(…...

技术分享 | 如何写好测试用例?
对于软件测试工程师来说,设计测试用例和提交缺陷报告是最基本的职业技能。是非常重要的部分。一个好的测试用例能够指示测试人员如何对软件进行测试。在这篇文章中,我们将介绍测试用例设计常用的几种方法,以及如何编写高效的测试用例。 ## 一…...

quarkus的一些注解1
path 用于指定一个类或者方法的URL路径前缀。 Inject 将一个依赖注入到一个类或方法中 Get 用于指定一个处理HTTP GET请求 Produce 注解用于指定一个方法返回的内容类型。例如,Produces(MediaType.TEXT_PLAIN) 表示该方法返回一个纯文本类型的内容 QuarkusIn…...
初学Redis(Redis的启动以及字符串String)
首先使用在Windows PowerShell中输入指令来启动Redis: redis-server.exe 然后通过指令连接Redis: redis-cli 上图的127.0.0.1是计算机的回送地址 ,6379是默认端口 上述代码中创建了两个键,注意Redis中严格区分大小写࿰…...

C++ opencv基本用法【学习笔记(九)】
这篇博客为修改过后的转载,因为没有转载链接,所以选了原创 文章目录 一、vs code 结合Cmake debug1.1 配置tasks.json1.2 配置launch.json 二、图片、视频、摄像头读取显示2.1 读取图片并显示2.2 读取视频文件并显示2.3 读取摄像头并写入文件 三、图片基…...

理财和银保区别
理财和银保在以下六个方面存在区别: 产品性质:银行理财是银行发行的理财产品,属于金融投资,主要投向债券、票据等固定收益类资产。银保产品是保险公司发行的保险产品,属于保障投资,除了固定收益类资产外&am…...
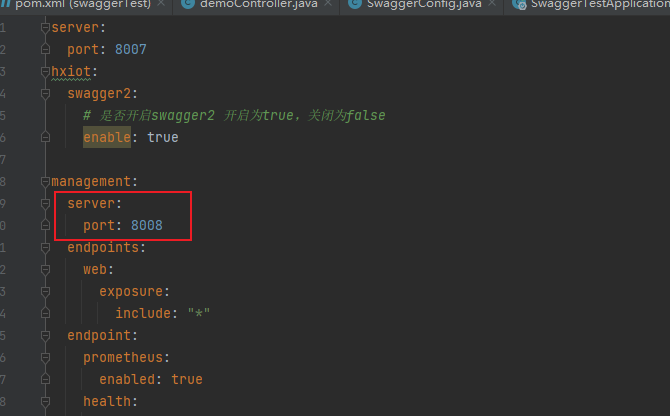
一文浅入Springboot+mybatis-plus+actuator+Prometheus+Grafana+Swagger2.9.2开发运维一体化
Swagger是一个规范和完整的框架,用于生成、描述、调用和可视化 RESTFUL风格的Web服务,是非常流行的API表达工具。 Swagger能够自动生成完善的 RESTFUL AP文档,,同时并根据后台代码的修改同步更新,同时提供完整的测试页面来调试API。 Prometheus 是一个开源的服务监控系统和时…...
【日常】爬虫技巧进阶:textarea的value修改与提交问题(以智谱清言为例)
序言 记录一个近期困扰了一些时间的问题。 我很喜欢在爬虫中遇到问题,因为这意味着在这个看似简单的事情里还是有很多值得去探索的新东西。其实本身爬虫也是随着前后端技术的不断更新在进步的。 文章目录 序言Preliminary1 问题缘起1.1 Selenium长文本输入阻塞1.2…...
:高精度乘法真题代码)
C++知识点总结(6):高精度乘法真题代码
一、高精度数 低精度数 #include <iostream> #include <cstring> using namespace std;int main() {// 存储并输入两个数字 char a_str[1005] {};long long b;cin >> a_str >> b;// 特例先行:结果是0的情况if (a 0 || b 0){cout <&…...

Polygon zkEVM的Dragon Fruit和Inca Berry升级
1. Polygon zkEVM的Dragon Fruit升级 2023年8月31日,Polygon zkEVM团队宣称启动了其Mainnet Beta的Dragon Fruit升级的10天timelock,预计将于2023年9月11日激活。 Dragon Fruit升级点有: 改进了网络支持了最新的以太坊opcode——PUSH0 1.…...

【计算机网络学习之路】网络基础1
文章目录 前言一. 计算机网络发展局域网和广域网 二. 网络协议三. OSI七层模型四. TCP/IP四层(五层)模型五. 计算机体系结构与网络协议栈六. 协议形式及局域网通信数据包封装与分用 七. 跨网络通信八. MAC地址与网络通信的理解结束语 前言 本系列文章是…...

HTTP/2.0协议详解
前言 HTTP/2.0:互联网通信的革新标准 随着互联网技术的飞速发展,HTTP协议作为互联网应用最广泛的通信协议,也在不断演进和优化。HTTP/2.0是HTTP协议的最新版本,它旨在提供更高效、更安全、更快速的互联网连接。 一、HTTP/2.0的优…...

Python中的Random模块详解:生成随机数与高级应用
在Python编程中,随机数生成是许多应用的基础之一。random模块为我们提供了生成伪随机数的丰富工具,从简单的随机数生成到复杂的应用场景,都有很多功能可以探索。本文将深入介绍random模块的各个方面,通过详实的示例代码࿰…...
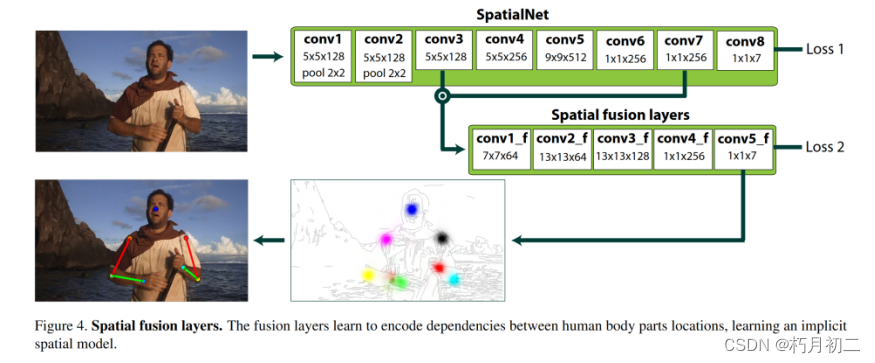
(论文阅读32/100)Flowing convnets for human pose estimation in videos
32.文献阅读笔记 简介 题目 Flowing convnets for human pose estimation in videos 作者 Tomas Pfister, James Charles, and Andrew Zisserman, ICCV, 2015. 原文链接 https://arxiv.org/pdf/1506.02897.pdf 关键词 Human Pose Estimation in Videos 研究问题 视频…...
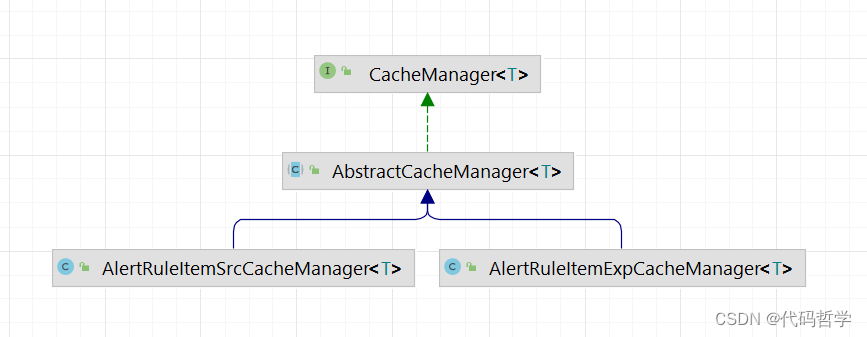
【设计一个缓存--针对各种类型的缓存】
设计一个缓存--针对各种类型的缓存 1. 设计顶层接口2. 设计抽象类 -- AbstractCacheManager3. 具体子类3.1 -- AlertRuleItemExpCacheManager3.2 -- AlertRuleItemSrcCacheManager 4. 类图关系 1. 设计顶层接口 // 定义为一个泛型接口,提供给抽象类使用 public interface Cach…...

Django部署时静态文件配置的坑
Django部署时静态文件配置配置的坑 近期有个需求是用django进行开发部署,结果发现静态文件配置的坑是真的多,另外网上很多的内容也讲不清楚原理,就是这样这样,又那样那样,进了不少坑,这里记录一下关于css,…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...

软件工程教学评价
王海林老师您好。 您的《软件工程》课程成功地将宏观的理论与具体的实践相结合。上半学期的理论教学中,您通过丰富的实例,将“高内聚低耦合”、SOLID原则等抽象概念解释得十分透彻,让这些理论不再是停留在纸面的名词,而是可以指导…...
