LeetCode 2342. 数位和相等数对的最大和:哈希表
【LetMeFly】2342.数位和相等数对的最大和:哈希表
力扣题目链接:https://leetcode.cn/problems/max-sum-of-a-pair-with-equal-sum-of-digits/
给你一个下标从 0 开始的数组 nums ,数组中的元素都是 正 整数。请你选出两个下标 i 和 j(i != j),且 nums[i] 的数位和 与 nums[j] 的数位和相等。
请你找出所有满足条件的下标 i 和 j ,找出并返回 nums[i] + nums[j] 可以得到的 最大值 。
示例 1:
输入:nums = [18,43,36,13,7] 输出:54 解释:满足条件的数对 (i, j) 为: - (0, 2) ,两个数字的数位和都是 9 ,相加得到 18 + 36 = 54 。 - (1, 4) ,两个数字的数位和都是 7 ,相加得到 43 + 7 = 50 。 所以可以获得的最大和是 54 。
示例 2:
输入:nums = [10,12,19,14] 输出:-1 解释:不存在满足条件的数对,返回 -1 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 109
方法一:哈希表
我们只需要建立一个哈希表,维护哈希表中“和为 k e y key key的最大的两个数”即可。
具体怎么做呢?
遍历数组中的元素 t t t,如果 t t t的和在哈希表中,那么就保留“哈希表中”和“ t t t”中较大的两个元素。
这里有一个小技巧:可以保持哈希表中的两个元素的相对顺序为第一个元素不小于第二个元素,这样替换时只需要比较 t t t和哈希表对应元素的第二个元素即可。
- 时间复杂度 O ( l e n ( n u m s ) ) O(len(nums)) O(len(nums))
- 空间复杂度 O ( l e n ( n u m s ) ) O(len(nums)) O(len(nums))
AC代码
C++
inline int getSum(int n) {int ans = 0;while (n) {ans += n % 10;n /= 10;}return ans;
}class Solution {
public:int maximumSum(vector<int>& nums) {unordered_map<int, pair<int, int>> ma;int ans = -1;for (int t : nums) {int s = getSum(t);if (t > ma[s].second) {ma[s].second = t;}if (ma[s].first < ma[s].second) {swap(ma[s].first, ma[s].second);}if (ma[s].second) {ans = max(ans, ma[s].first + ma[s].second);}}return ans;}
};
Python
class Solution:def getSum(self, n: int) -> int:ans = 0while n:ans += n % 10n //= 10return ansdef maximumSum(self, nums: List[int]) -> int:ans = -1ma = dict()for t in nums:s = self.getSum(t)if s in ma:if t > ma[s][1]:ma[s][1] = tif ma[s][0] < ma[s][1]:ma[s][0], ma[s][1] = ma[s][1], ma[s][0]ans = max(ans, sum(ma[s]))else:ma[s] = [t, 0]return ans
同步发文于CSDN,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/134476645
相关文章:

LeetCode 2342. 数位和相等数对的最大和:哈希表
【LetMeFly】2342.数位和相等数对的最大和:哈希表 力扣题目链接:https://leetcode.cn/problems/max-sum-of-a-pair-with-equal-sum-of-digits/ 给你一个下标从 0 开始的数组 nums ,数组中的元素都是 正 整数。请你选出两个下标 i 和 j&…...
Vulkan渲染引擎开发教程 一、开发环境搭建
一 安装 Vulkan SDK Vulkan SDK 就是我们要搞的图形接口 首先到官网下载SDK并安装 https://vulkan.lunarg.com/sdk/home 二 安装 GLFW 窗口库 GLFW是个跨平台的小型窗口库,也就是显示窗口,图形的载体 去主页下载并安装,https://www.glfw.…...
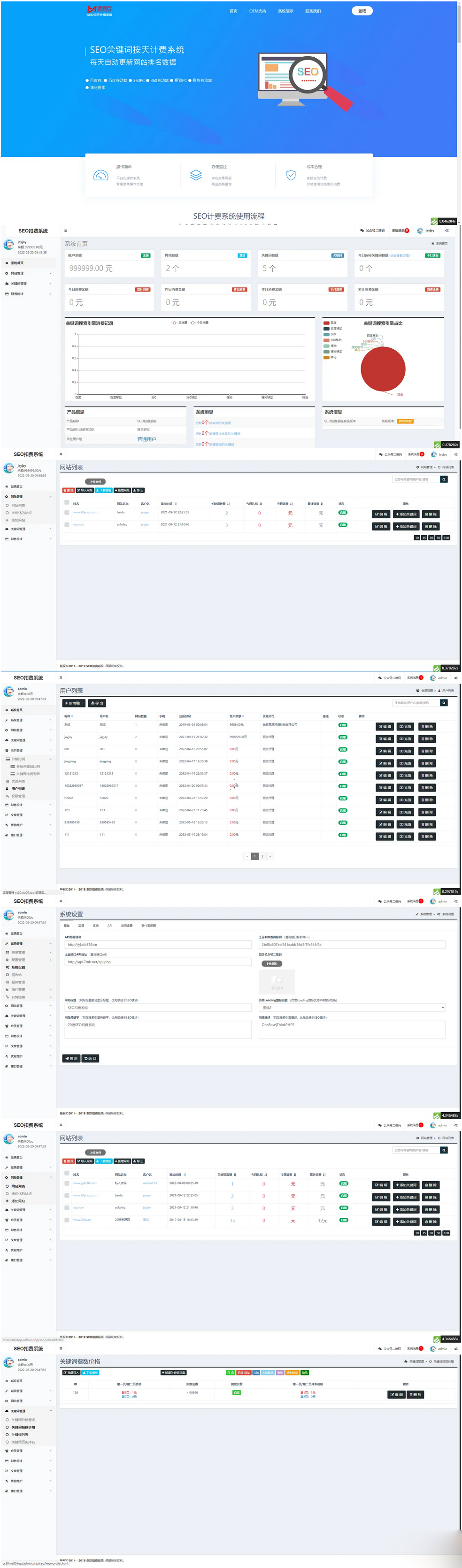
(带教程)商业版SEO关键词按天计费系统:关键词排名优化、代理服务、手机自适应及搭建教程
源码简介: 1、会员管理: 该系统分为三个级别的会员流程:总站管理员、代理与会员(会员有普通会员、中级会员和高级会员三个等级)。总站管理员可以添加代理用户并为其充值余额,代理用户可以为普通用户充值余…...
IDEA 快捷键汇总
目录 1、altinsert 2、ctrl/ 3、altenter 4、alt回车 5、ctrlD 6、ctrlaltL 7、ctrl点击 8、alt左键向下拉 9、ctrlaltv 10、ctrlaltwint 1、altinsert 快速创建代码,可以快速创建类中get set tostring等方法 2、ctrl/ 单行注释 3、altenter…...

目标检测YOLO实战应用案例100讲-基于机器视觉的水稻病虫害监测预警
目录 前言 国内外研究现状 国外研究现状 国内研究现状 2 相关理论与技术...

OrthoNets:正交信道注意网络
文章目录 摘要1、简介2、相关工作3、方法4、实验设置及结果5、论述6、结论摘要 链接:https://arxiv.org/pdf/2311.03071v2.pdf 设计有效的通道注意力机制要求人们找到一种有损压缩方法,以实现最佳特征表示。尽管该领域近年来取得了进展,但仍然存在一个未解决的问题。FcaNet…...
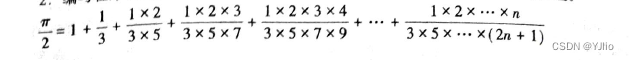
C_12练习题
一、单项选择题(本大题共20小题,每小题2分,共40分。在每小题给出的四个备选项中,选出一个正确的答案,并将所选项前的字母填写在答题纸的相应位置上。) C 风格的注释,也称块注释或多行注释,以()…...

导航守卫有哪三种?
导航守卫主要分为三种: 全局前置守卫:使用 router.beforeEach 注册,作用是在路由切换开始前进行拦截和处理,可以用来进行一些全局的权限校验、登录状态检查等操作。 全局解析守卫:使用 beforeResolve 注册,…...

强烈 推荐 13 个 Web前端在线代码IDE
codesandbox.io(国外,提供免费空间) 网址:https://codesandbox.io/ CodeSandbox 专注于构建完整的 Web 应用程序,支持多种流行的前端框架和库,例如 React、Vue 和 Angular。它提供了一系列增强的功能&…...

网络协议 WebSocket
一、介绍 WebSocket 是基于 TCP 的一种新的网络协议。它实现了浏览器与服务器全双工通信——浏览器和服务器只需要完成一次握手,两者之间就可以创建持久性的连接, 并进行双向数据传输 1、HTTP协议和WebSocket协议对比 HTTP 是短连接WebSocket 是长连接H…...

路径操作 合法路径名
python中路径的三种合法表示:在路径前面加上r、分隔符使用/。 在路径前面加上r python中在前面加上r,是防止字符转义。 例如:这样一个路径: \Undergraduate\School\Programme\Python_Learnpython会将这个字符串的**\和\后面的…...

JavaEE初阶 01 计算机是如何工作的
前言 今天开始进行对JavaEE的一些基本总结,希望大家能在阅读中有所收获,如有错误还望多多指正. 1.冯诺依曼体系结构 这个体系结构相信学计算机的同学都不陌生,但是你真的知道这个体系结构说的是什么嘛?请听我娓娓道来.首先我先给出一张冯诺依曼体系结构的简图 你可以理解为当前…...

【shell 常用脚本30例】
先了解下编写Shell过程中注意事项 开头加解释器:#!/bin/bash语法缩进,使用四个空格;多加注释说明。命名建议规则:全局变量名大写、局部变量小写,函数名小写,名字体现出实际作用。默认变量是全局的…...

【我和Python算法的初相遇】——体验递归的可视化篇
🌈个人主页: Aileen_0v0 🔥系列专栏:PYTHON数据结构与算法学习系列专栏💫"没有罗马,那就自己创造罗马~" 目录 递归的起源 什么是递归? 利用递归解决列表求和问题 递归三定律 递归应用-整数转换为任意进制数 递归可视化 画…...
【C语言的秘密】密探—深究C语言中多组输入的秘密!
场景引入: 你是否在刷题过程中,经常遇到以下场景呢? 场景一: 场景二: 从这些题上都能看见输入描述中提出了一条多组输入,那啥是多组输入?如何实现它呢? 多组输入:在输入…...

ClickHouse 语法优化规则
ClickHouse 的 SQL 优化规则是基于RBO(Rule Based Optimization),下面是一些优化规则 1 准备测试用表 1)上传官方的数据集 将visits_v1.tar和hits_v1.tar上传到虚拟机,解压到clickhouse数据路径下 // 解压到clickhouse数据路径 sudo tar -xvf…...

3-运行第一个docker image-hello world
CentOS7.9下安装完成docker后,我们开始部署第一个docker image-hello world 1.以root用户登录CentOS7.9服务器,拉取centos7 images 命令: docker pull hello-world [root@centos79 ~]# docker pull hello-world Using default tag: latest latest: Pulling from library…...
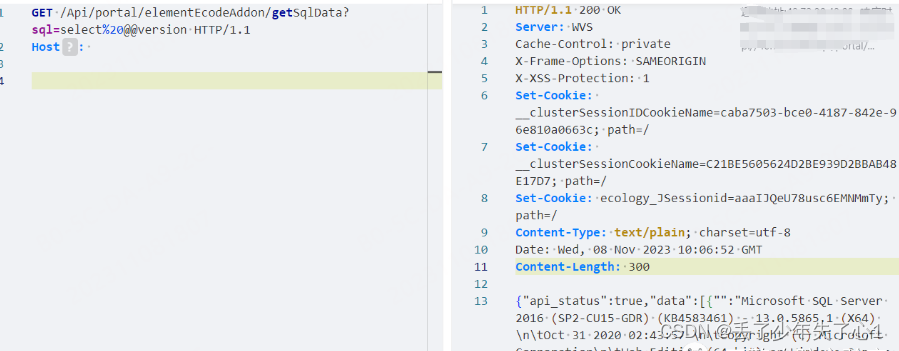
【漏洞复现】泛微e-Weaver SQL注入
漏洞描述 泛微e-Weaver(FANWEI e-Weaver)是一款广泛应用于企业数字化转型领域的集成协同管理平台。作为中国知名的企业级软件解决方案提供商,泛微软件(广州)股份有限公司开发和推广了e-Weaver平台。 泛微e-Weaver旨在…...
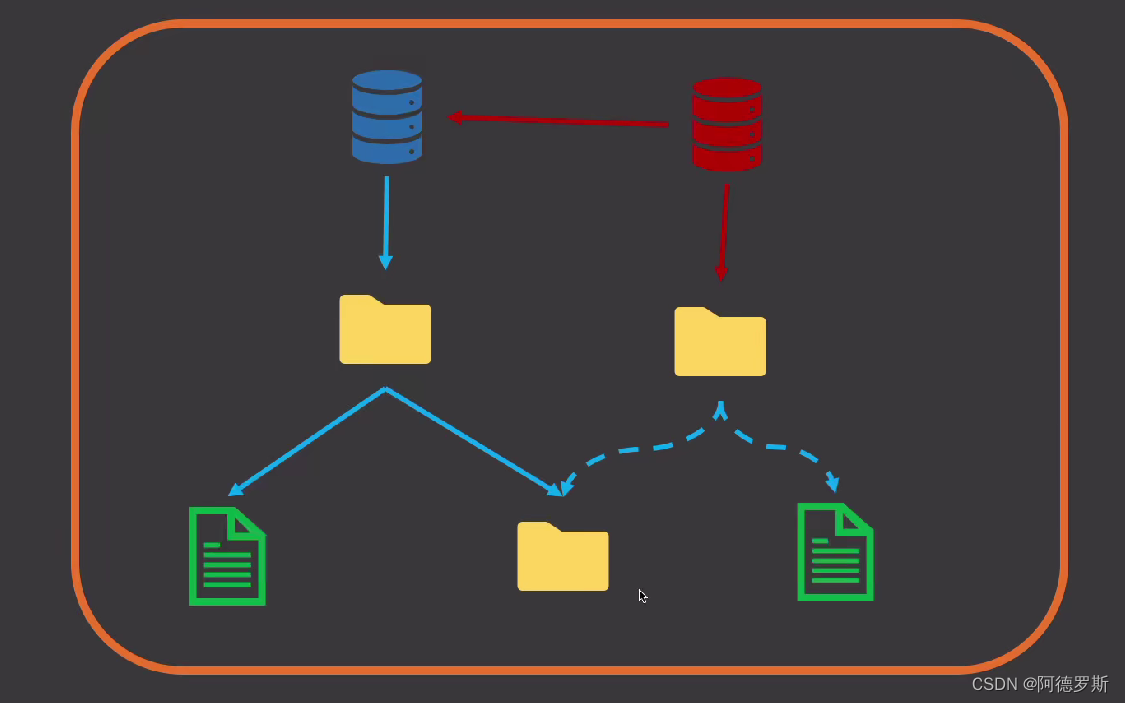
「git 系列」git 如何存储代码的?
这里写自定义目录标题 git 文件存储位置git 数据模型示例分析分析前准备命令哈希值 具体示例 不同版本的提交,git 做了什么工作?snapshot vs delta-based vs backup参考资料 git 文件存储位置 想要了解如何存储,首先需要知道存储位置。 当我…...
IDEA 集成 Docker 插件一键部署 SpringBoot 应用
目录 前言IDEA 安装 Docker 插件配置 Docker 远程服务器编写 DockerFileSpringBoot 部署配置SpringBoot 项目部署结语 前言 随着容器化技术的崛起,Docker成为了现代软件开发的关键工具。在Java开发中,Spring Boot是一款备受青睐的框架,然而&…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
