AM@函数展开成幂级数@间接法@常用麦克劳林幂级数展开公式
文章目录
- 间接法推导幂级数展开
- 常用麦克劳林幂级数展开公式
- 应用
- 例
- 例
- 例
间接法推导幂级数展开
-
已知函数的幂级数展开公式间接推导其他函数幂级数
-
使用原始的推导公式推导函数的幂级数展开是繁琐不便的,需要分别计算各项系数 a n = f ( n ) ( 0 ) n ! a_{n}=\frac{f^{(n)}(0)}{n!} an=n!f(n)(0),最后考察余项 R n ( x ) R_{n}(x) Rn(x)是否趋于0
-
尤其是其中研究余项在初等函数中也不是容易的事
-
间接法包括:
- 幂级数运算(四则运算,逐项求导,逐项积分)
- 变量代换法
-
这些间接方法不仅计算简单,而且避开了对余项的研究
常用麦克劳林幂级数展开公式
-
利用以下基础展开式(直接法推得),可以推出许多函数的幂级数展开式
-
下面( 1 ∼ 4 1\sim{4} 1∼4)是基础幂级数,推出后面得新幂级数:
- e x e^{x} ex= ∑ n = 0 ∞ 1 n ! x n \sum_{n=0}^{\infin}\frac{1}{n!}x^{n} ∑n=0∞n!1xn, x ∈ ( − ∞ , + ∞ ) x\in(-\infin,+\infin) x∈(−∞,+∞)
- e x e^{x} ex= 1 + x + x 2 2 ! + ⋯ 1+x+\frac{x^2}{2!}+\cdots 1+x+2!x2+⋯
- sin x \sin{x} sinx= ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! \sum_{n=0}^{\infin} (-1)^{n}\frac{x^{2n+1}}{(2n+1)!} ∑n=0∞(−1)n(2n+1)!x2n+1, x ∈ ( − ∞ , + ∞ ) x\in(-\infin,+\infin) x∈(−∞,+∞)
- sin x \sin{x} sinx= x − x 3 3 ! + x 5 5 ! − ⋯ x-\frac{x^3}{3!}+\frac{x^{5}}{5!}-\cdots x−3!x3+5!x5−⋯
- 1 1 − x \frac{1}{1-x} 1−x1= ∑ n = 0 ∞ x n \sum_{n=0}^{\infin}x^{n} ∑n=0∞xn, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- 这个级数是最简单的幂级数,因为这是级数的前 n n n项和是容易表示的,即首项为 1 1 1,公比为 x x x的前 n n n项和: 1 ( 1 − x n ) 1 − x \frac{1(1-x^{n})}{1-x} 1−x1(1−xn),当 n → ∞ n\to{\infin} n→∞时 s n → 1 1 − x s_{n}\to{\frac{1}{1-x}} sn→1−x1, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- 也可以利用幂级数的通用求法来求
- 1 1 − x \frac{1}{1-x} 1−x1= 1 + x + x 2 + ⋯ 1+x+x^2+\cdots 1+x+x2+⋯
- 1 1 + x \frac{1}{1+x} 1+x1= ∑ n = 0 ∞ ( − 1 ) n x n \sum_{n=0}^{\infin}(-1)^{n}x^{n} ∑n=0∞(−1)nxn, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- 和第3个类似
- 也可以由 x ∈ ( − 1 , 1 ) x\in{(-1,1)} x∈(−1,1), − x ∈ ( − 1 , 1 ) -x\in(-1,1) −x∈(−1,1),将式(3)的 x x x替换为 − x -x −x,得到(4)
- 1 1 + x \frac{1}{1+x} 1+x1= 1 − x + x 2 − ⋯ 1-x+x^2-\cdots 1−x+x2−⋯
- ln ( x + 1 ) \ln(x+1) ln(x+1)= ∑ n = 1 ∞ ( − 1 ) n − 1 1 n x n \sum_{n=1}^{\infin}(-1)^{n-1}\frac{1}{n}x^{n} ∑n=1∞(−1)n−1n1xn, x ∈ ( − 1 , 1 ] x\in(-1,1] x∈(−1,1]👺
- 对式(4)两边做 [ 0 , x ] [0,x] [0,x]上的积分,即
- 左边: ∫ 0 x 1 x + 1 d x \int_{0}^{x}\frac{1}{x+1}\mathrm{d}x ∫0xx+11dx= ∫ 0 x 1 t + 1 d t \int_{0}^{x}\frac{1}{t+1}\mathrm{d}t ∫0xt+11dt= ln ∣ t + 1 ∣ ∣ 0 x \ln|t+1||_{0}^{x} ln∣t+1∣∣0x= ln ∣ x + 1 ∣ \ln|x+1| ln∣x+1∣= ln ( x + 1 ) \ln(x+1) ln(x+1), x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- 右边: ∑ n = 0 ∞ ( − 1 ) n x n \sum_{n=0}^{\infin}(-1)^{n}x^{n} ∑n=0∞(−1)nxn= ∑ n = 0 ∞ ∫ 0 x ( − 1 ) n t n d t \sum_{n=0}^{\infin}\int_{0}^{x}(-1)^{n}t^{n}\mathrm{d}t ∑n=0∞∫0x(−1)ntndt= ∑ n = 0 ∞ ( − 1 ) n 1 n + 1 x n + 1 \sum_{n=0}^{\infin}(-1)^{n}\frac{1}{n+1}x^{n+1} ∑n=0∞(−1)nn+11xn+1= ∑ n = 1 ∞ ( − 1 ) n − 1 1 n x n \sum_{n=1}^{\infin}(-1)^{n-1}\frac{1}{n}x^{n} ∑n=1∞(−1)n−1n1xn, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- ln ( x + 1 ) \ln(x+1) ln(x+1)= x − x 2 2 + x 3 3 − ⋯ x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots x−2x2+3x3−⋯
- 对式(4)两边做 [ 0 , x ] [0,x] [0,x]上的积分,即
- cos x \cos{x} cosx= ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! \sum_{n=0}^{\infin} (-1)^{n}\frac{x^{2n}}{(2n)!} ∑n=0∞(−1)n(2n)!x2n, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- 对式(2)两边求导,立即得到此式
- cos x \cos{x} cosx= 1 − x 2 2 ! + x 4 4 ! − ⋯ 1-\frac{x^2}{2!}+\frac{x^{4}}{4!}-\cdots 1−2!x2+4!x4−⋯
- 1 1 + x 2 \frac{1}{1+x^2} 1+x21= ∑ n = 0 ∞ ( − 1 ) n x 2 n \sum_{n=0}^{\infin}(-1)^{n}x^{2n} ∑n=0∞(−1)nx2n, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- 对于 x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1), x 2 ∈ ( − 1 , 1 ) x^2\in(-1,1) x2∈(−1,1)
- 所以将式(4)中 x x x替换为 x 2 x^2 x2即得此式
- 1 1 + x 2 \frac{1}{1+x^2} 1+x21= 1 − x 2 + x 4 − ⋯ 1-x^2+x^{4}-\cdots 1−x2+x4−⋯
- arctan x \arctan{x} arctanx= ∑ n = 0 ∞ ( − 1 ) n 1 2 n + 1 x 2 n + 1 \sum_{n=0}^{\infin}(-1)^{n}\frac{1}{2n+1}x^{2n+1} ∑n=0∞(−1)n2n+11x2n+1, x ∈ [ − 1 , 1 ] x\in[-1,1] x∈[−1,1]👺
- 对式(7)两边做 [ 0 , x ] [0,x] [0,x]上的积分,即得此式
- arctan x \arctan{x} arctanx= x − x 3 3 + x 5 5 + ⋯ x-\frac{x^3}{3}+\frac{x^5}{5}+\cdots x−3x3+5x5+⋯
- a x a^{x} ax= ∑ n = 0 ∞ ( ln a ) n n ! x n \sum_{n=0}^{\infin}\frac{(\ln{a})^{n}}{n!}x^{n} ∑n=0∞n!(lna)nxn, ( − ∞ < x < + ∞ ) (-\infin<x<+\infin) (−∞<x<+∞)
- 将式(1)中的 x x x替换为 ln a x \ln{a^{x}} lnax,即 x ln a x\ln{a} xlna即可
- e ln a x e^{\ln{a^{x}}} elnax= a x a^{x} ax
- e x e^{x} ex= ∑ n = 0 ∞ 1 n ! x n \sum_{n=0}^{\infin}\frac{1}{n!}x^{n} ∑n=0∞n!1xn, x ∈ ( − ∞ , + ∞ ) x\in(-\infin,+\infin) x∈(−∞,+∞)
-
补充一个直接法推得幂级数展开:
- f ( x ) f(x) f(x)= ( 1 + x ) m (1+x)^{m} (1+x)m= 1 + m x + m ( m − 1 ) 2 ! x 2 + ⋯ + m ( m − 1 ) ⋯ ( m − n + 1 ) n ! x n + ⋯ 1+mx+\frac{m(m-1)}{2!}x^2+\cdots+\frac{m(m-1)\cdots{(m-n+1)}}{n!}x^{n}+\cdots 1+mx+2!m(m−1)x2+⋯+n!m(m−1)⋯(m−n+1)xn+⋯, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
- 其中 m m m为任意实数
- 当 m ∈ N + m\in\mathrm{N_{+}} m∈N+,展开式就是二项式定理: ( 1 + x ) m (1+x)^{m} (1+x)m= ∑ k = 0 m C m k x k \sum_{k=0}^{m}C_{m}^{k}{x}^{k} ∑k=0mCmkxk
- f ( x ) f(x) f(x)= ( 1 + x ) m (1+x)^{m} (1+x)m= 1 + m x + m ( m − 1 ) 2 ! x 2 + ⋯ + m ( m − 1 ) ⋯ ( m − n + 1 ) n ! x n + ⋯ 1+mx+\frac{m(m-1)}{2!}x^2+\cdots+\frac{m(m-1)\cdots{(m-n+1)}}{n!}x^{n}+\cdots 1+mx+2!m(m−1)x2+⋯+n!m(m−1)⋯(m−n+1)xn+⋯, x ∈ ( − 1 , 1 ) x\in(-1,1) x∈(−1,1)
应用
- 利用上述公式推导陌生函数的幂级数展开实例
例
-
把 f ( x ) f(x) f(x)= ( 1 − x ) ln ( 1 + x ) (1-x)\ln(1+x) (1−x)ln(1+x)展开成 x x x得幂级数
-
由 ln ( 1 + x ) \ln(1+x) ln(1+x)= ∑ n = 1 ∞ ( − 1 ) n − 1 n x n \sum_{n=1}^{\infin}\frac{(-1)^{n-1}}{n}x^{n} ∑n=1∞n(−1)n−1xn, x ∈ ( − 1 , 1 ] x\in{(-1,1]} x∈(−1,1]
-
f ( x ) f(x) f(x)= ( 1 − x ) ∑ n = 1 ∞ ( − 1 ) n − 1 n x n (1-x)\sum_{n=1}^{\infin}\frac{(-1)^{n-1}}{n}x^{n} (1−x)∑n=1∞n(−1)n−1xn
- 思路1:
- = ∑ n = 1 ∞ ( − 1 ) n − 1 n x n ( 1 − x ) \sum_{n=1}^{\infin}\frac{(-1)^{n-1}}{n}x^{n}(1-x) ∑n=1∞n(−1)n−1xn(1−x),这不是 x x x得幂级数
- 思路2:分配律分开处理,对齐通项幂次和求和下标求和
- 先对齐通项幂(变动求和下标的起点),在对其求和下标(将多于的项移到求和号外计算)
- = ∑ n = 1 ∞ ( − 1 ) n − 1 n x n \sum_{n=1}^{\infin}\frac{(-1)^{n-1}}{n}x^{n} ∑n=1∞n(−1)n−1xn- ∑ n = 1 ∞ ( − 1 ) n − 1 n x n + 1 \sum_{n=1}^{\infin}\frac{(-1)^{n-1}}{n}x^{n+1} ∑n=1∞n(−1)n−1xn+1
- = ∑ n = 1 ∞ ( − 1 ) n − 1 n x n \sum_{n=1}^{\infin}\frac{(-1)^{n-1}}{n}x^{n} ∑n=1∞n(−1)n−1xn- ∑ n = 2 ∞ ( − 1 ) n − 2 n − 1 x n \sum_{n=2}^{\infin}\frac{(-1)^{n-2}}{n-1}x^{n} ∑n=2∞n−1(−1)n−2xn
- = x + ∑ n = 2 ∞ ( − 1 ) n − 1 n x n x+\sum_{n=2}^{\infin}\frac{(-1)^{n-1}}{n}x^{n} x+∑n=2∞n(−1)n−1xn- ∑ n = 2 ∞ ( − 1 ) n − 2 n − 1 x n \sum_{n=2}^{\infin}\frac{(-1)^{n-2}}{n-1}x^{n} ∑n=2∞n−1(−1)n−2xn
- = x + ∑ n = 2 ∞ ( − 1 ) n − 1 ( 2 n − 1 ) n ( n − 1 ) x n x+\sum_{n=2}^{\infin} \frac{(-1)^{n-1}(2n-1)}{n(n-1)}x^{n} x+∑n=2∞n(n−1)(−1)n−1(2n−1)xn, x ∈ ( − 1 , 1 ] x\in{(-1,1]} x∈(−1,1]
- 思路1:
-
例
- 有理分式的展开,通常采用 1 1 − x \frac{1}{1-x} 1−x1= ∑ n = 0 ∞ x n \sum_{n=0}^{\infin}x^{n} ∑n=0∞xn
(1)或 1 1 + x \frac{1}{1+x} 1+x1= ∑ n = 0 ∞ ( − 1 ) n x n \sum_{n=0}^{\infin}(-1)^{n}x^{n} ∑n=0∞(−1)nxn(1-1)代换- (1)和(1-1)之间形式转换是很简单的, 1 1 + x \frac{1}{1+x} 1+x1= 1 1 − ( − x ) \frac{1}{1-(-x)} 1−(−x)1,
- 而若展开为 x − x 0 x-x_0 x−x0的形式,则需要配项(换元: t = x − x 0 t=x-x_0 t=x−x0),令 g = g ( t ) = g ( x − x 0 ) g=g(t)=g(x-x_0) g=g(t)=g(x−x0),使得形式靠近 1 1 − t ( x ) \frac{1}{1-t(x)} 1−t(x)1
- 例如,设分母为 P ( x ) P(x) P(x),则应将 P ( x ) P(x) P(x)变形为 P ( x ) = k ( 1 + g ( x − x 0 ) ) P(x)=k(1+g(x-x_0)) P(x)=k(1+g(x−x0)), k k k为常数
- 特别的,如果能够确定 g ( x − x 0 ) g(x-x_0) g(x−x0)是 x x x的一次式,即可设 g ( x − x 0 ) = m ( x − x 0 ) g(x-x_0)=m(x-x_0) g(x−x0)=m(x−x0),那么 P ( x ) = k ( 1 + m ( x − x 0 ) ) P(x)=k(1+m(x-x_0)) P(x)=k(1+m(x−x0)), m , k m,k m,k为常数,即 P ( x ) P(x) P(x)= k m x + k − k m x 0 kmx+k-kmx_0 kmx+k−kmx0,利用系数比较法可以分别确定 k , m k,m k,m
- 从而可以确定 g = g ( x − x 0 ) g=g(x-x_0) g=g(x−x0),用 g g g代替式(1)或(1-1)中的 x x x,并且收敛区间为 g ∈ ( − 1 , 1 ) g\in(-1,1) g∈(−1,1)的解集
- 总之,这个过程是需要一定的尝试和计算才能正确变形为复合要求的形式
- f ( x ) f(x) f(x)= 1 x 2 + 4 x + 3 \frac{1}{x^2+4x+3} x2+4x+31展开为 x − 1 x-1 x−1的幂级数
- f ( x ) f(x) f(x)= 1 ( x + 1 ) ( x + 3 ) \frac{1}{(x+1)(x+3)} (x+1)(x+3)1= 1 2 ( 1 + x ) \frac{1}{2(1+x)} 2(1+x)1- 1 2 ( 3 + x ) \frac{1}{2(3+x)} 2(3+x)1
- = 1 4 1 1 + x − 1 2 \frac{1}{4}\frac{1}{1+\frac{x-1}{2}} 411+2x−11- 1 8 ( 1 + x − 1 4 ) \frac{1}{8(1+\frac{x-1}{4})} 8(1+4x−1)1
(2) - 2 ( 1 + x ) 2(1+x) 2(1+x)= k ( 1 + m ( x − 1 ) ) k(1+m(x-1)) k(1+m(x−1))
(2-1),即 2 x + 2 2x+2 2x+2= k m x + k − k m kmx+k-km kmx+k−km- 比较系数可得 m k = 2 mk=2 mk=2, k − k m = 2 k-km=2 k−km=2,解得 k = 4 k=4 k=4, m = 1 2 m=\frac{1}{2} m=21,代入式(2-1),得 4 ( 1 + x − 1 2 ) 4(1+\frac{x-1}{2}) 4(1+2x−1)
- 从而 1 2 ( 1 + x ) \frac{1}{2(1+x)} 2(1+x)1= 1 4 ( 1 + x − 1 2 ) \frac{1}{4(1+\frac{x-1}{2})} 4(1+2x−1)1
- 类似的, 2 ( 3 + x ) 2(3+x) 2(3+x)= k ( 1 + m ( x − 1 ) ) k(1+m(x-1)) k(1+m(x−1)),即 6 + 2 x 6+2x 6+2x= k m x + k − k m kmx+k-km kmx+k−km,比较两边系数,得 m k = 2 mk=2 mk=2, k − k m = 6 k-km=6 k−km=6,得 k = 8 k=8 k=8, m = 1 4 m=\frac{1}{4} m=41,
- 从而 1 2 ( 3 + x ) \frac{1}{2(3+x)} 2(3+x)1= 1 8 ( 1 + x − 1 4 ) \frac{1}{8(1+\frac{x-1}{4})} 8(1+4x−1)1
- 比较系数可得 m k = 2 mk=2 mk=2, k − k m = 2 k-km=2 k−km=2,解得 k = 4 k=4 k=4, m = 1 2 m=\frac{1}{2} m=21,代入式(2-1),得 4 ( 1 + x − 1 2 ) 4(1+\frac{x-1}{2}) 4(1+2x−1)
- = 1 4 1 1 + x − 1 2 \frac{1}{4}\frac{1}{1+\frac{x-1}{2}} 411+2x−11- 1 8 ( 1 + x − 1 4 ) \frac{1}{8(1+\frac{x-1}{4})} 8(1+4x−1)1
- 而 1 4 1 1 + x − 1 2 \frac{1}{4}\frac{1}{1+\frac{x-1}{2}} 411+2x−11= 1 4 ∑ n = 0 ∞ ( − 1 ) n 2 n ( x − 1 ) n \frac{1}{4}\sum_{n=0}^{\infin}\frac{(-1)^{n}}{2^{n}}(x-1)^{n} 41∑n=0∞2n(−1)n(x−1)n
(3), x − 1 2 ∈ ( − 1 , 1 ) \frac{x-1}{2}\in(-1,1) 2x−1∈(−1,1),解得 x ∈ ( − 1 , 3 ) x\in(-1,3) x∈(−1,3), - 类似的, 1 8 ( 1 + x − 1 4 ) \frac{1}{8(1+\frac{x-1}{4})} 8(1+4x−1)1= 1 8 ∑ n = 0 ∞ ( − 1 ) n 4 n ( x − 1 ) n \frac{1}{8}\sum_{n=0}^{\infin}\frac{(-1)^{n}}{4^{n}}(x-1)^{n} 81∑n=0∞4n(−1)n(x−1)n,
(4)x ∈ ( − 3 , 5 ) x\in(-3,5) x∈(−3,5) - 所以 f ( x ) f(x) f(x)= ∑ n = 0 ∞ ( − 1 ) n ( 1 2 n + 2 − 1 2 2 n + 3 ) ( x − 1 ) n \sum_{n=0}^{\infin}(-1)^{n}(\frac{1}{2^{n+2}}-\frac{1}{2^{2n+3}})(x-1)^{n} ∑n=0∞(−1)n(2n+21−22n+31)(x−1)n
(5)- 这里(3),(4)无法对求和号的通项直接相加,需要将求和号外的系数移入求和号
- 这样(3)改写为 ∑ n = 0 ∞ ( − 1 ) n 2 n + 2 ( x − 1 ) n \sum_{n=0}^{\infin}\frac{(-1)^{n}}{2^{n+2}}(x-1)^{n} ∑n=0∞2n+2(−1)n(x−1)n
- (4)改写为 ∑ n = 0 ∞ 1 2 3 ( − 1 ) n 2 2 n ( x − 1 ) n \sum_{n=0}^{\infin} \frac{1}{2^{3}}\frac{(-1)^{n}}{2^{2n}}(x-1)^{n} ∑n=0∞23122n(−1)n(x−1)n= ∑ n = 0 ∞ ( − 1 ) n 2 2 n + 3 ( x − 1 ) n \sum_{n=0}^{\infin} \frac{(-1)^{n}}{2^{2n+3}}(x-1)^{n} ∑n=0∞22n+3(−1)n(x−1)n,取(3,4)中较小的收敛半径,即 x ∈ ( − 1 , 3 ) x\in(-1,3) x∈(−1,3)
- f ( x ) f(x) f(x)= 1 ( x + 1 ) ( x + 3 ) \frac{1}{(x+1)(x+3)} (x+1)(x+3)1= 1 2 ( 1 + x ) \frac{1}{2(1+x)} 2(1+x)1- 1 2 ( 3 + x ) \frac{1}{2(3+x)} 2(3+x)1
例
- sin x \sin{x} sinx展开成 x − π 4 x-\frac{\pi}{4} x−4π得幂级数
- 注意,被展开的函数时 sin x \sin{x} sinx,而不是 sin ( x − π 4 ) \sin{(x-\frac{\pi}{4})} sin(x−4π)
- 后者展开成 x − π 4 x-\frac{\pi}{4} x−4π直接用 x − π 4 x-\frac{\pi}{4} x−4π代替 sin x \sin{x} sinx的幂级数展开
- 但是前者要复杂,需要做变形
- sin x \sin{x} sinx= sin ( π 4 + ( x − π 4 ) ) \sin(\frac{\pi}{4}+(x-\frac{\pi}{4})) sin(4π+(x−4π))
- = sin π 4 cos ( x − π 4 ) + cos π 4 sin ( x − π 4 ) \sin\frac{\pi}{4}\cos(x-\frac{\pi}{4})+\cos\frac{\pi}{4}\sin(x-\frac{\pi}{4}) sin4πcos(x−4π)+cos4πsin(x−4π)
- = 1 2 [ cos ( x − π 4 ) + sin ( x − π 4 ) ] \frac{1}{\sqrt{2}}[\cos(x-\frac{\pi}{{4}})+\sin(x-\frac{\pi}{4})] 21[cos(x−4π)+sin(x−4π)]
- 现在用 x − π 4 x-\frac{\pi}{4} x−4π分别代替 cos x , sin x \cos{x},\sin{x} cosx,sinx幂级数展开中的 x x x
- 然后合并,最后可得 sin x \sin{x} sinx= 1 2 [ ∑ n = 0 ∞ ( − 1 ) n ( 2 n + 1 ) ! ( x − π 4 ) 2 n + 1 ] \frac{1}{\sqrt{2}}[\sum_{n=0}^{\infin}\frac{(-1)^{n}}{(2n+1)!}(x-\frac{\pi}{4})^{2n+1}] 21[∑n=0∞(2n+1)!(−1)n(x−4π)2n+1], x ∈ ( − ∞ , + ∞ ) x\in(-\infin,+\infin) x∈(−∞,+∞)
相关文章:

AM@函数展开成幂级数@间接法@常用麦克劳林幂级数展开公式
文章目录 间接法推导幂级数展开常用麦克劳林幂级数展开公式应用例例例 间接法推导幂级数展开 已知函数的幂级数展开公式间接推导其他函数幂级数 使用原始的推导公式推导函数的幂级数展开是繁琐不便的,需要分别计算各项系数 a n f ( n ) ( 0 ) n ! a_{n}\frac{f^{(n)}(0)}{n!}…...

LeetCode994.腐烂的橘子
看完题我觉得这不是和上一道岛屿的题一样简单嘛,然后写了将近2个小时才写出来,我的思路就是,用check()先对grid检查一下,是否有以下情况: (如果有1的周围都是空,则这个位置用不腐烂,…...
【开源】基于Vue和SpringBoot的康复中心管理系统
项目编号: S 056 ,文末获取源码。 \color{red}{项目编号:S056,文末获取源码。} 项目编号:S056,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 普通用户模块2.2 护工模块2.3 管理员…...
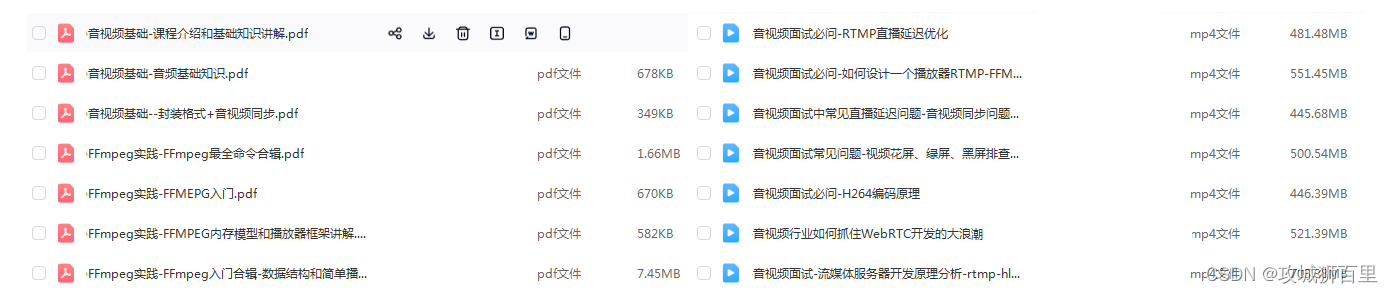
【音视频基础】AVI文件格式
AVI文件采用的是RIFF文件结构方式。波形音频wave,MIDI和数字视频AVI都采用这种格式存储。 AVI文件的整体结构如下图所示 构造RIFF文件的基本单元叫做数据块(Chunk),每个数据块包含3个部分 4字节的数据块标记(或者叫…...
,剑指offer,力扣)
图书馆整理I(从尾到头打印列表),剑指offer,力扣
目录 题目地址: 我们直接看题解吧: 解题方法: 难度分析: 审题目事例提示: 解题思路(辅助栈): 代码(递归): 代码(列表插入): 相似题目对…...

C++编写的多线程自动爬虫程序
目录 引言 一、程序的设计 二、程序的实现 三、程序的测试 四、优化与改进 五、代码示例 总结 引言 随着互联网的快速发展,网络爬虫程序已经成为数据采集、信息处理的重要工具。C作为一种高效的编程语言,具有高效的并发处理能力和丰富的网络编程…...

SMB信息泄露的利用
一、背景 今天分享SMB信息泄露,SMB(Server Message Block)网络通信协议,早些时候被用于Web链接和客户端与服务器之间的信息通信,现在大部分Web页面使用HTTP协议,在web领域应用较少。另一方面SMB协议还是被…...
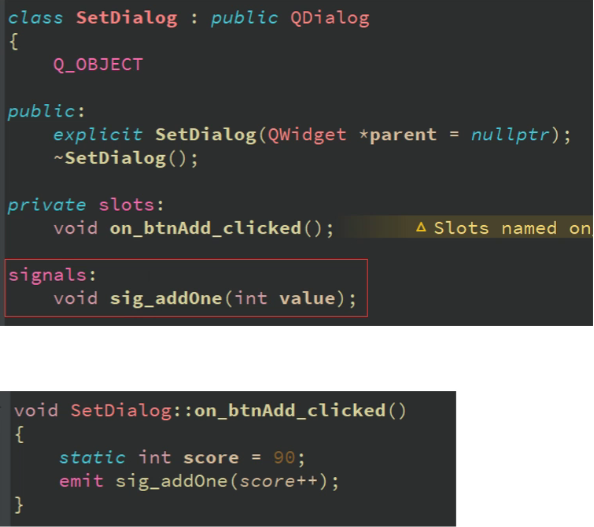
QT自定义信号,信号emit,信号参数注册
qt如何自定义信号 使用signals声明返回值是void在需要发送信号的地方使用 emit 信号名字(参数)进行发送 在需要链接的地方使用connect进行链接 ct进行链接...

06.webpack性能优化--构建速度
优化babel-loaderhappyPackIgnorePluginparalleUglifyPluginnoParse自动刷新 1 happypack多进程打包 js单线程,开启多进程打包提高构建速度(特别是多核CPU) const HappyPack require(happypack)module.exports smart(webpackCommonConf,…...

11-15 周三 softmax 回归学习
11-15 周三 softmax 回归学习 时间版本修改人描述2023年11月15日11:17:27V0.1宋全恒新建文档 简介 softmax分享可以参考什么是softmax 回归估计一个连续值,分类预测一个离散类别。 恶意软件的判断 回归和分类 分类可以认为从回归的单输出变成多输出 B站学习 softm…...

React新手必懂的知识点
react思想:组件化开发 React 的核心概念是组件化开发,将用户界面拆分成独立的可复用组件。学习如何创建和使用 React 组件,以及组件之间的数据传递和通信是非常重要的。 React的思想就是拆分组件与使用组件。 import React from react;// 定…...

es为什么这么快
es为什么这么快的方式 es的基于Lucene开源搜索引擎,负责文件存储和搜索,支持http请求,以json形式展示 这样介绍你有可能有点迷糊我们详细解释 es 使用的倒排索引的方式,进行数据存储方式,给每一个字段创建索引&…...
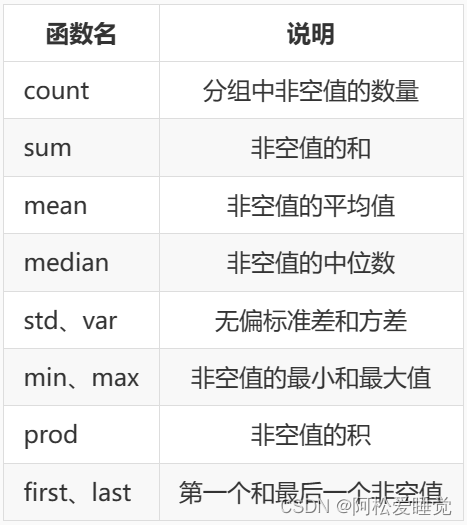
Pandas分组聚合_Python数据分析与可视化
Pandas分组聚合 分组单列和多列分组Series 系列分组通过数据类型或者字典分组获取单个分组对分组进行迭代 聚合应用单个聚合函数应用多个聚合函数自定义函数传入 agg() 中对不同的列使用不同的聚合函数 分组聚合的流程主要有三步: 分割步骤将 DataFrame 按照指定的…...
VMware17虚拟机Linux安装教程(详解附图,带VMware Workstation 17 Pro安装)
一、安装 VMware 附官方下载链接(VM 17 pro):https://download3.vmware.com/software/WKST-1701-WIN/VMware-workstation-full-17.0.1-21139696.exe 打开下载好的VMware Workstation 17 Pro安装包; 点击下一步; 勾选我…...
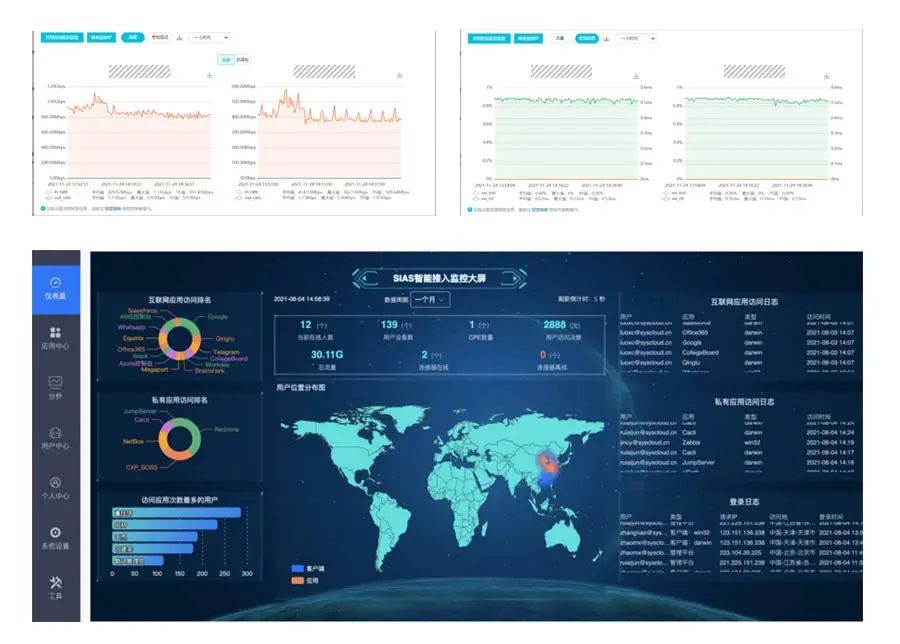
基于SDN技术构建多平面业务承载网络
随着企业数字化的浪潮席卷各个行业,传统网络架构面临着更为复杂和多样化的挑战。企业正在寻找一种全面适应数字化需求的网络解决方案。随着软件定义网络(SDN)的发展,“多业务SDN一张网”解决方案为企业提供了一种全新的网络架构&a…...
关于卓越服务的调研报告
NetSuite知识会发起的本次调研从2023年11月2日开始,到11月12日结束。16日已向参与调研的朋友邮件回复,感谢您的付出!今朝分享此报告,各位同学参考。 调研问题与反馈总结 问题1:您能想到哪些服务组织能够提供高满意度&…...

ubuntu22.04换源
1、系统信息 lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 22.04.3 LTS Release: 22.04 Codename: jammy2、进入 /etc/apt/ 目录: cd /etc/apt/ 3、备份默认源文件 sudo cp sources.list sources.list_bak 4、编…...
03. Python中的语句
1、前言 在《Python基础数据类型》一文中,我们了解了Python中的基础数据类型,今天我们继续了解下Python中的语句和函数。 2、语句 在Python中常用的语句可以大致分为两类:条件语句、循环语句。 2.1、条件语句 条件语句就是我们编码时常见…...
Linux CentOS7 添加网卡
一台主机中安装多块网卡,有许多优势。可以实现多项功能。 为了学习网卡参数的设置,可以为主机添加多块网卡。与添加磁盘一样,要在VMware中设置。利用图形化方式或命令行查看或设置网卡。本文仅初步讨论添加、查看与删除网卡,有关…...

2311rust,到54版本更新
1.50.0稳定版 常量泛型数组索引 继续向稳定的常量泛型迈进,此版本为[T;N]数组,添加了ops::Index和IndexMut的实现. fn second<C>(container: &C) -> &C::Output whereC: std::ops::Index<usize> ?Sized, {&container[1] } fn main() {let arra…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
C++中vector类型的介绍和使用
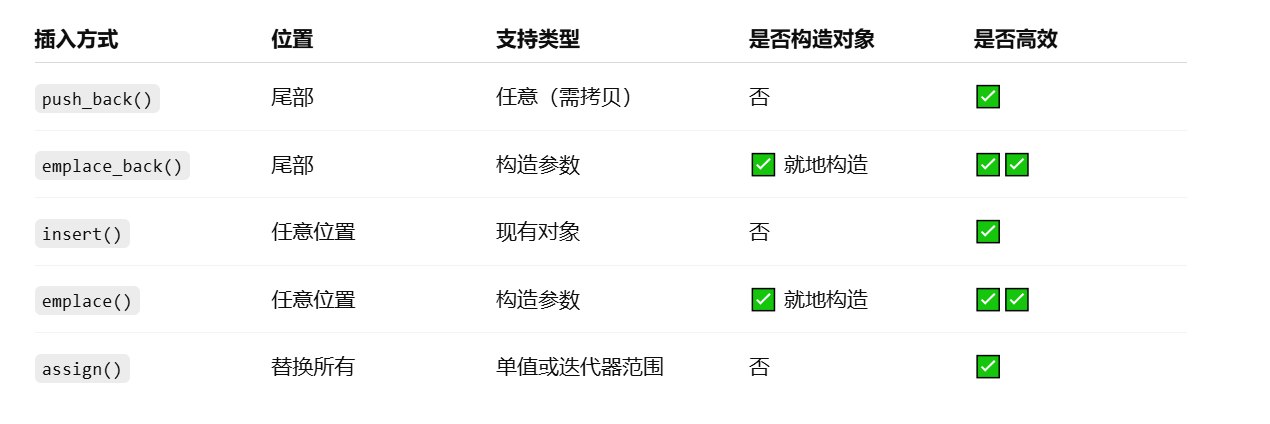
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...

Q1起重机指挥理论备考要点分析
Q1起重机指挥理论备考要点分析 一、考试重点内容概述 Q1起重机指挥理论考试主要包含三大核心模块:安全技术知识(占40%)、指挥信号规范(占30%)和法规标准(占30%)。考试采用百分制,8…...
