数据结构与算法(六):图结构
图是一种比线性表和树更复杂的数据结构,在图中,结点之间的关系是任意的,任意两个数据元素之间都可能相关。图是一种多对多的数据结构。
一、基本概念
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
注意:线性表中可以没有元素,称为空表。树中可以没有结点,叫做空树。但是在图中不允许没有顶点,可以没有边。
基本术语:
-
无向边:若顶点Vi和Vj之间的边没有方向,称这条边为无向边(Edge),用(Vi,Vj)来表示。
-
无向图(Undirected graphs):图中任意两个顶点的边都是无向边。
-
有向边:若从顶点Vi到Vj的边有方向,称这条边为有向边,也称为弧(Arc),用<Vi, Vj>来表示,其中Vi称为弧尾(Tail),Vj称为弧头(Head)。
-
有向图(Directed graphs):图中任意两个顶点的边都是有向边。
-
简单图:不存在自环(顶点到其自身的边)和重边(完全相同的边)的图
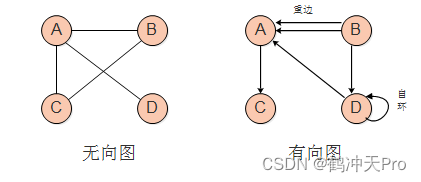
-
无向完全图:无向图中,任意两个顶点之间都存在边。
-
有向完全图:有向图中,任意两个顶点之间都存在方向相反的两条弧。
-
稀疏图;有很少条边或弧的图称为稀疏图,反之称为稠密图。
-
权(Weight):表示从图中一个顶点到另一个顶点的距离或耗费。
-
网:带有权重的图
-
度:与特定顶点相连接的边数;
-
出度、入度:有向图中的概念,出度表示以此顶点为起点的边的数目,入度表示以此顶点为终点的边的数目;
-
环:第一个顶点和最后一个顶点相同的路径;
-
简单环:除去第一个顶点和最后一个顶点后没有重复顶点的环;
-
连通图:任意两个顶点都相互连通的图;
-
极大连通子图:包含竟可能多的顶点(必须是连通的),即找不到另外一个顶点,使得此顶点能够连接到此极大连通子图的任意一个顶点;
-
连通分量:极大连通子图的数量;
-
强连通图:此为有向图的概念,表示任意两个顶点a,b,使得a能够连接到b,b也能连接到a 的图;
-
生成树:n个顶点,n-1条边,并且保证n个顶点相互连通(不存在环);
-
最小生成树:此生成树的边的权重之和是所有生成树中最小的;
-
AOV网(Activity On Vertex Network ):在有向图中若以顶点表示活动,有向边表示活动之间的先后关系
-
AOE网(Activity On Edge Network):在带权有向图中若以顶点表示事件,有向边表示活动,边上的权值表示该活动持续的时间
二、图的存储结构
由于图的结构比较复杂,任意两个顶点之间都可能存在关系,因此用简单的顺序存储来表示图是不可能,而若使用多重链表的方式(即一个数据域多个指针域的结点来表示),这将会出现严重的空间浪费或操作不便。这里总结一下常用的表示图的方法:
1、邻接矩阵
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称邻接矩阵)存储图中的边或弧的信息。
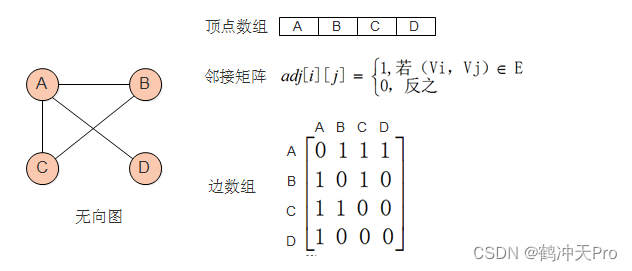
无向图由于边不区分方向,所以其邻接矩阵是一个对称矩阵。邻接矩阵中的0表示边不存在,主对角线全为0表示图中不存在自环。
带权有向图的邻接矩阵:
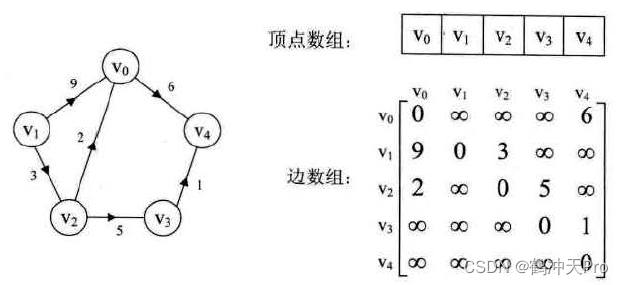
在带权有向图的邻接矩阵中,数字表示权值weight,「无穷」表示弧不存在。由于权值可能为0,所以不能像在无向图的邻接矩阵中那样使用0来表示弧不存在。
代码:
/*** 有向图的邻接矩阵实现*/
public class Digraph {private int vertexsNum;private int edgesNum;private int[][] arc;public Digraph(int[][] data, int vertexsNum) {this.vertexsNum = vertexsNum;this.edgesNum = data.length;arc = new int[vertexsNum][vertexsNum];for (int i = 0; i < vertexsNum; i++) {for (int j = 0; j < vertexsNum; j++) {arc[i][j] = Integer.MAX_VALUE;}}for (int i = 0; i < data.length; i++) {int tail = data[i][0];int head = data[i][1];arc[tail][head] = 1;}}//用于测试,返回一个顶点的邻接点public Iterable<Integer> adj(int vertex) {Set<Integer> set = new HashSet<>();for (int i = 0; i < vertexsNum; i++) {if (arc[vertex][i] != Integer.MAX_VALUE)set.add(i);}return set;}public static void main(String[] args) {int[][] data = {{0,3},{1,0},{1,2},{2,0},{2,1},};Digraph wd = new Digraph(data,4);for(int i :wd.adj(1)) {System.out.println(i);} }
}
优缺点:
- 优点:结构简单,操作方便
- 缺点:对于稀疏图,这种实现方式将浪费大量的空间。
2、邻接表
邻接表是一种将数组与链表相结合的存储方法。其具体实现为:将图中顶点用一个一维数组存储,每个顶点Vi的所有邻接点用一个单链表来存储。这种方式和树结构中孩子表示法一样。
对于有向图其邻接表结构如下:
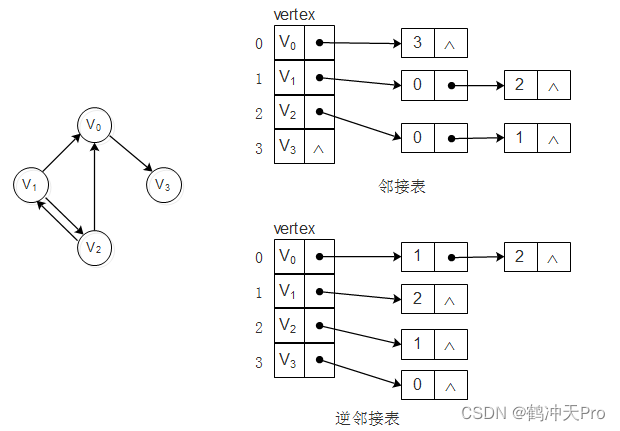
有向图的邻接表是以顶点为弧尾来存储边表的,这样很容易求一个顶点的出度(顶点对应单链表的长度),但若求一个顶点的入度,则需遍历整个图才行。这时可以建立一个有向图的逆邻接表即对每个顶点v都建立一个弧头尾v的单链表。如上图所示。
代码:
/*** 有向图的邻接表实现**/
public class AdjListDigraph {private class EdgeNode {int index;EdgeNode next;EdgeNode(int index, EdgeNode next){this.index = index;this.next = next;}}private class VertexNode {int id;EdgeNode headNode;}private VertexNode[] vertexs;private int vertexsNum;private int edgesNum;public AdjListDigraph(int[][] data, int vertexsNum) {this.vertexsNum = vertexsNum;this.edgesNum = data.length;vertexs = new VertexNode[vertexsNum];for (int i = 0; i < vertexs.length; i++) {vertexs[i] = new VertexNode();vertexs[i].id = i; //}for (int i = 0; i < data.length; i++) {int index = data[i][1];EdgeNode next = vertexs[data[i][0]].headNode;EdgeNode eNode = new EdgeNode(index,next);vertexs[data[i][0]].headNode = eNode; //头插法}}//用于测试,返回一个顶点的邻接点public Iterable<Integer> adj(int index) {Set<Integer> set = new HashSet<>();EdgeNode current = vertexs[index].headNode;while(current != null) {VertexNode node = vertexs[current.index];set.add(node.id);current = current.next;}return set;}public static void main(String[] args) {int[][] data = {{0,3},{1,0},{1,2},{2,0},{2,1},};AdjListDigraph ald = new AdjListDigraph(data,4);for(int i :ald.adj(1)) {System.out.println(i);} }
}
本算法的时间复杂度为 O(N + E),其中N、E分别为顶点数和边数,邻接表实现比较适合表示稀疏图。
3、十字链表
十字链表(Orthogonal List)是将邻接表和逆邻接表相结合的存储方法,它解决了邻接表(或逆邻接表)的缺陷,即求入度(或出度)时必须遍历整个图。
十字链表的结构如下:
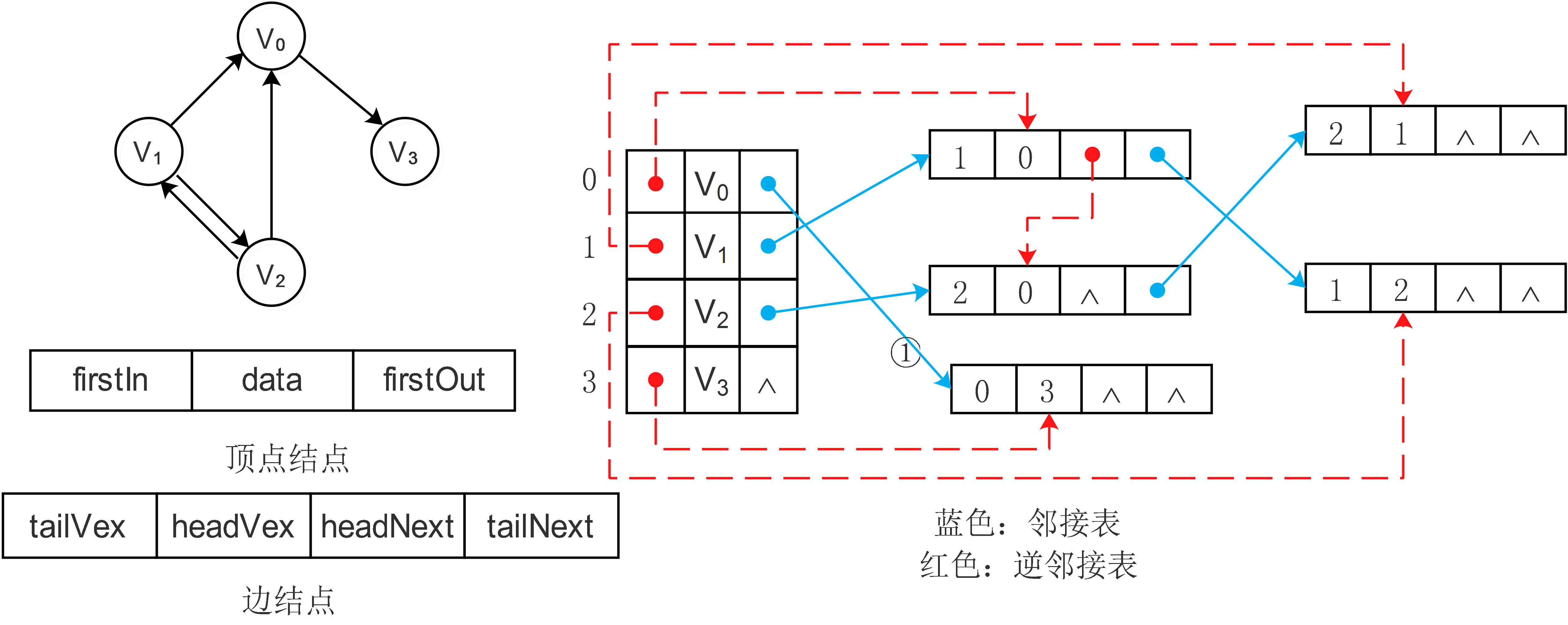
图中:
- firstIn表示入边表(即是逆邻接表中的单链表)头指针,firstOut表示出边表(即是邻接表中的单链表)头指针,data表示顶点数据。
- tailVex表示边的起点在顶点数组中的下标,tailNext值出边表指针域,指向起点相同的下一条边。
- headVex表示边的终点在顶点数组中的下标,headNext指入边表指针域,指向终点相同的下一条边。
代码实现:
/*** 有向图的十字链表实现**/
public class OrthogonalList {private class EdgeNode {int tailVex;int headVex;EdgeNode headNext;EdgeNode tailNext;public EdgeNode(int tailVex, int headVex, EdgeNode headNext, EdgeNode tailNext) {super();this.tailVex = tailVex;this.headVex = headVex;this.headNext = headNext;this.tailNext = tailNext;}}private class VertexNode {int data;EdgeNode firstIn;EdgeNode firstOut;}private VertexNode[] vertexs;private int vertexsNum;private int edgesNum;public OrthogonalList(int[][] data, int vertexsNum) {this.vertexsNum = vertexsNum;this.edgesNum = data.length;vertexs = new VertexNode[vertexsNum];for (int i = 0; i < vertexs.length; i++) {vertexs[i] = new VertexNode();vertexs[i].data = i; //}//关键for (int i = 0; i < data.length; i++) {int tail = data[i][0];int head = data[i][1];EdgeNode out = vertexs[tail].firstOut;EdgeNode in = vertexs[head].firstIn;EdgeNode eNode = new EdgeNode(tail,head,in,out);vertexs[tail].firstOut = eNode;vertexs[head].firstIn = eNode;}}//返回一个顶点的出度public int outDegree(int index) {int result = 0;EdgeNode current = vertexs[index].firstOut;while(current != null) {current = current.tailNext;result++;}return result;}//返回一个顶点的入度public int inDegree(int index) {int result = 0;EdgeNode current = vertexs[index].firstIn;while(current != null) {current = current.headNext;result++;}return result;}public static void main(String[] args) {int[][] data = {{0,3},{1,0},{1,2},{2,0},{2,1},};OrthogonalList orth = new OrthogonalList(data,4);System.out.println("顶点1的出度为" + orth.outDegree(1));System.out.println("顶点1的入度为" + orth.inDegree(1));}
}
十字链表创建图算法的时间复杂度和邻接表相同都为O(N + E)。在有图的应用中推荐使用。
三、图的遍历
从图的某个顶点出发,遍历图中其余顶点,且使每个顶点仅被访问一次,这个过程叫做图的遍历(Traversing Graph)。对于图的遍历通常有两种方法:深度优先遍历和广度优先遍历。
1、深度优先遍历
深度优先遍历(Depth First Search,简称DFS),也成为深度优先搜索。
遍历思想:基本思想:首先从图中某个顶点v0出发,访问此顶点,然后依次从v相邻的顶点出发深度优先遍历,直至图中所有与v路径相通的顶点都被访问了;若此时尚有顶点未被访问,则从中选一个顶点作为起始点,重复上述过程,直到所有的顶点都被访问。
深度优先遍历用递归实现比较简单,只需用一个递归方法来遍历所有顶点,在访问某一个顶点时:
- 将它标为已访问
- 递归的访问它的所有未被标记过的邻接点
深度优先遍历的过程:
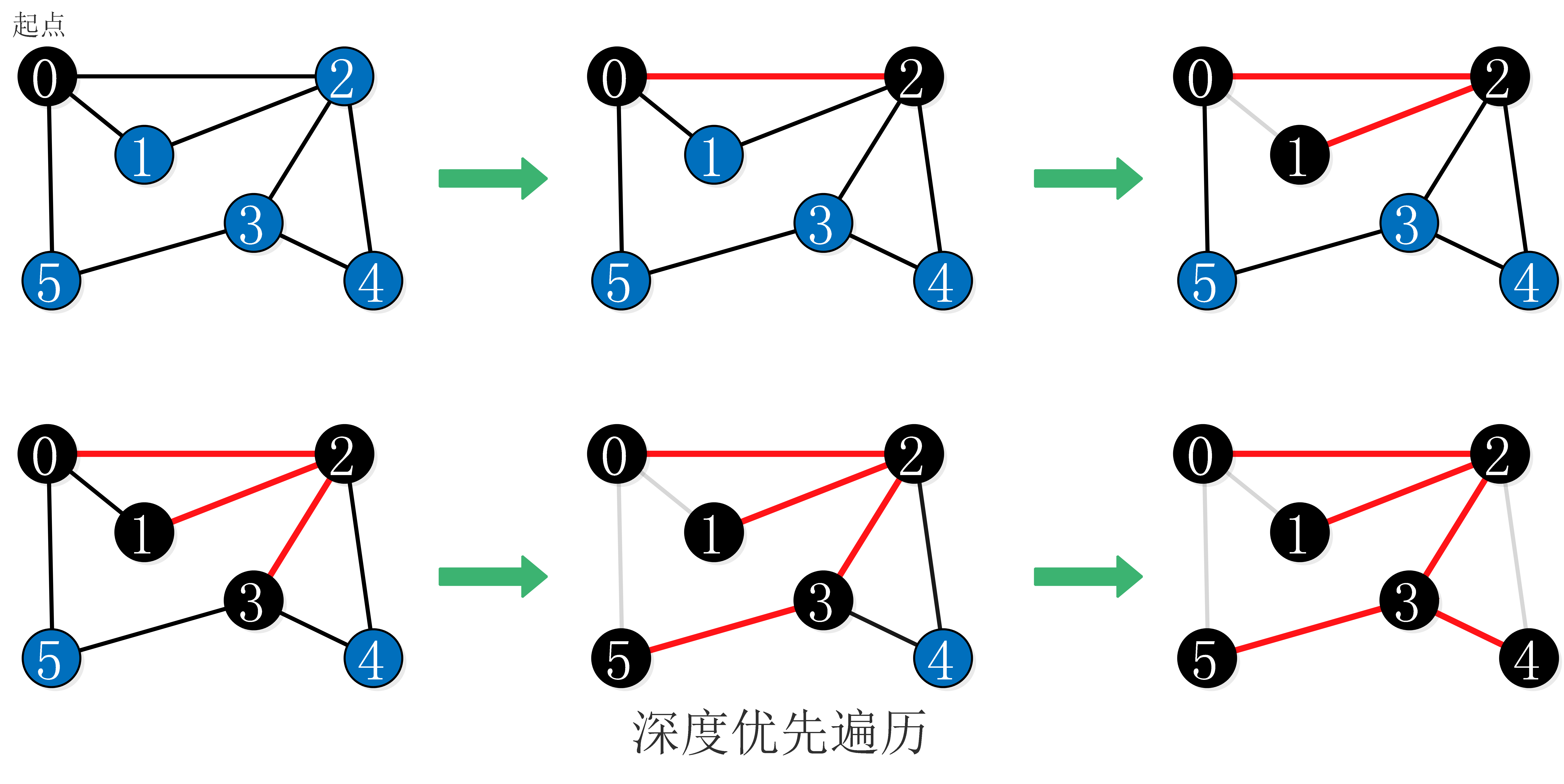
代码如下:
public class DFSTraverse {private boolean[] visited;//从顶点index开始遍历public DFSTraverse(Digraph graph, int index) {visited = new boolean[graph.getVertexsNum()];dfs(graph,index);}private void dfs(Digraph graph, int index) {visited[index] = true;for(int i : graph.adj(index)) {if(!visited[i])dfs(graph,i); }}
}
2、广度优先遍历
广度优先遍历(Breadth First Search,简称BFS),又称为广度优先搜索
遍历思想:首先,从图的某个顶点v0出发,访问了v0之后,依次访问与v0相邻的未被访问的顶点,然后分别从这些顶点出发,广度优先遍历,直至所有的顶点都被访问完。
广度优先遍历的过程:
代码:
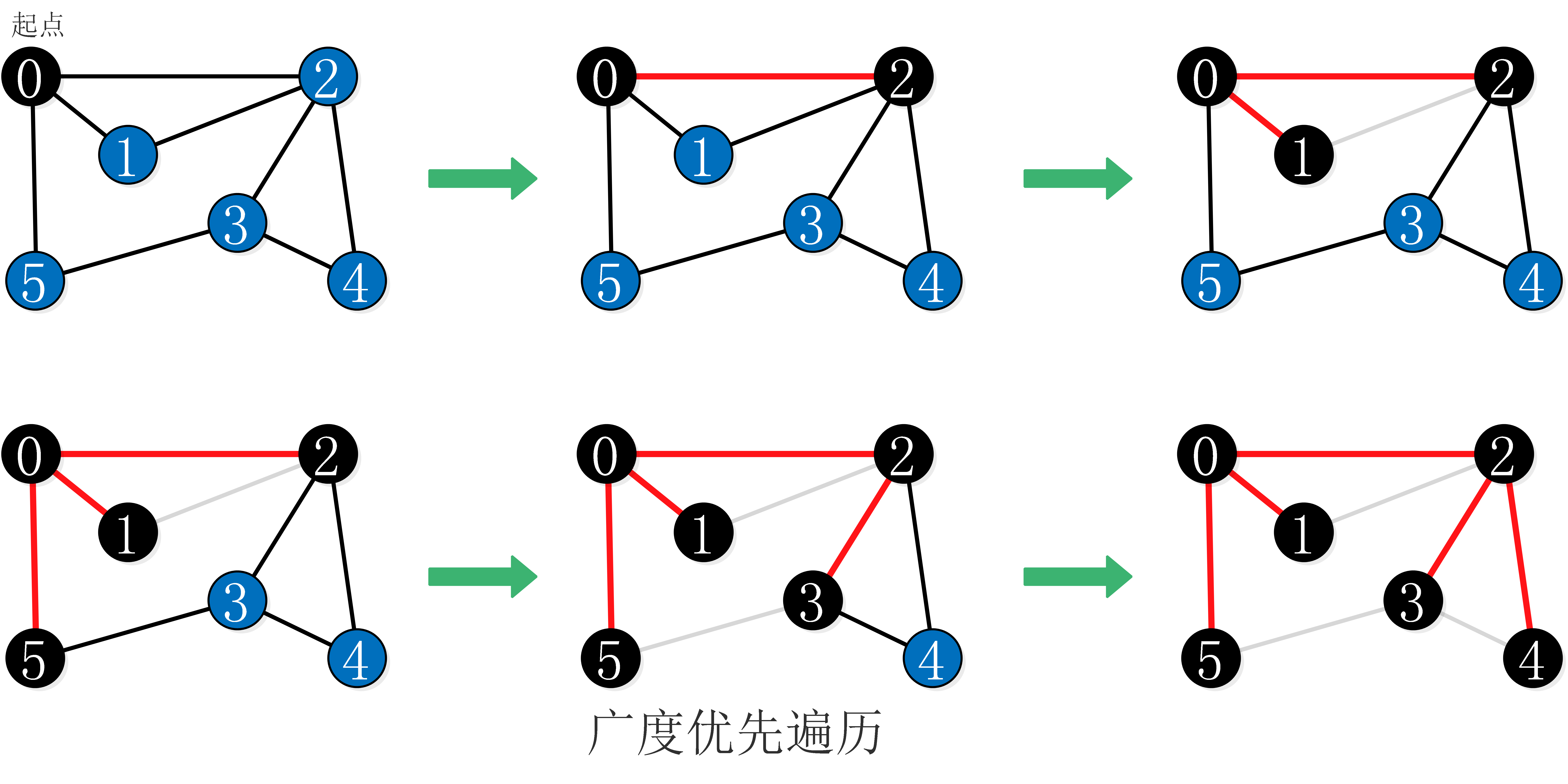
public class BFSTraverse {private boolean[] visited;public BFSTraverse(AdjListDigraph graph, int index) {visited = new boolean[graph.getVertexsNum()];bfs(graph,index);}private void bfs(AdjListDigraph graph, int index) {//在JSE中LinkedList实现了Queue接口Queue<Integer> queue = new LinkedList<>();visited[index] = true;queue.add(index);while(!queue.isEmpty()) {int vertex = queue.poll();for(int i : graph.adj(vertex)) {if(!visited[i]) {visited[i] = true;queue.offer(i);}}}}
}
四、最小生成树
图的生成树是它的一棵含有所有顶点的无环连通子图。一棵加权图的最小生成树(MST)是它的一棵权值(所有边的权值之和)最小的生成树。
计算最小生成树可能遇到的情况:
- 非连通的无向图,不存在最小生成树
- 权重不一定和距离成正比
- 权重可能是0或负数
- 若存在相等的权重,那么最小生成树可能不唯一
图的切分是将图的所有顶点分为两个非空且不重叠的两个集合。横切边是一条连接两个属于不同集合的顶点的边。
切分定理:在一幅加权图中,给定任意的切分,它的横切边中的权重最小者必然属于图的最小生成树。
切分定理是解决最小生成树问题的所有算法的基础。这些算法都是贪心算法。
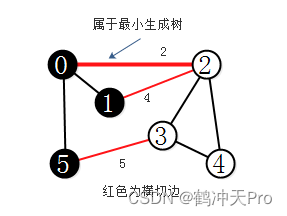
首先先构造一个带权的无向图,其代码如下:
//定义边
public class Edge implements Comparable<Edge>{private final int ver1;private final int ver2;private final Integer weight;public Edge(int ver1, int ver2, int weight) {super();this.ver1 = ver1;this.ver2 = ver2;this.weight = weight;}//返回一个顶点public int either() {return ver1;}//返回另一个顶点public int other(int vertex) {if (vertex == ver1)return ver2;else if(vertex == ver2)return ver1;else throw new RuntimeException("边不一致");}@Overridepublic int compareTo(Edge e) {return this.weight.compareTo(e.weight);}public Integer getWeight() {return weight;}@Overridepublic String toString() {return "Edge [" + ver1 + "," + ver2 +"]";}
}/*** 带权无向图的实现*/
public class WeightedGraph {private final int vertexsNum;private final int edgesNum;private List<Edge>[] adj;public WeightedGraph(int[][] data, int vertexsNum) {this.vertexsNum = vertexsNum;this.edgesNum = data.length;adj = (List<Edge>[]) new ArrayList[vertexsNum];for(int i=0; i<vertexsNum; i++) {adj[i] = new ArrayList<>();}for (int i = 0; i < data.length; i++) {Edge edge = new Edge(data[i][0],data[i][1],data[i][2]);int v = edge.either();adj[v].add(edge);adj[edge.other(v)].add(edge);}}public Iterable<Edge> adj(int vertex) {return adj[vertex];}public int getVertexsNum() {return vertexsNum;}public int getEdgesNum() {return edgesNum;}public Iterable<Edge> getEdges() {List<Edge> edges = new ArrayList<>();for(int i=0; i<vertexsNum; i++) {for(Edge e : adj[i]) {if(i > e.other(i)) { //无向图,防止将一条边加入两次edges.add(e);}}}return edges;}
}
1、Prim算法
每次将权值最小的横切边加入生成树中
1)、Prim算法的延迟实现
实现过程如下图:
从顶点0开始,首先将顶点0加入到树中(标记),顶点0和其它点的横切边(这里即为顶点0的邻接边)加入优先队列,将权值最小的横切边出队,加入生成树中。此时相当于也向树中添加了一个顶点2,接着将集合(顶点1,2组成)和另一个集合(除1,2的顶点组成)间的横切边加入到优先队列中,如此这般,直到队列为空。
注意:若横切边中另一个顶点在树中,则此边失效。
代码如下:
public class LazyPrimMST {private boolean[] visited; //标记顶点private LinkedQueue<Edge> mst; //存储最小生成树的边private MinPQ<Edge> pq; //优先队列,权值越最小优先级越高public LazyPrimMST(WeightedGraph wg) {visited = new boolean[wg.getVertexsNum()];mst = new LinkedQueue<Edge>();pq = new MinPQ<>(wg.getVertexsNum());visit(wg, 0); //从0点开始while(!pq.isEmpty()) {Edge e = pq.deQueue();int ver1 = e.either();int ver2 = e.other(ver1);if(visited[ver1] && visited[ver2]) {continue; //边失效}mst.enQueue(e);if(!visited[ver1])visit(wg, ver1);if(!visited[ver2])visit(wg, ver2);}}private void visit(WeightedGraph wg, int ver) {visited[ver] = true; //标记顶点for(Edge e : wg.adj(ver)) {if(!visited[e.other(ver)])pq.enQueue(e);}}public Iterable<Edge> getMST() {return mst;}public static void main(String[] args) {int[][] data = {{0, 2, 2},{0, 1, 4},{0, 5, 5},{1, 2, 3},{1, 5, 11},{1, 3, 7},{2, 3, 8},{2, 4, 10},{3, 5, 6},{3, 4, 1},{4, 5, 9}};WeightedGraph wg = new WeightedGraph(data,6);LazyPrimMST lpm = new LazyPrimMST(wg);for(Edge e : lpm.getMST()) {System.out.println(e);}}
}
其中,LinkedQueue类的代码在《数据结构与算法(三),栈与队列》中;而MinPQ类的代码与《数据结构与算法(五),优先队列》中MaxPQ类的代码几乎一样,只需将方法less中的小于号改为大于号即可。这里就不在给出代码了
此方法的时间复杂度为 O(ElogE),空间复杂度为 O(E)。其中,V为顶点个数,E为边数
2)、Prim算法即时实现
基于Prim算法的延迟实现,我们可以在优先队列中只保存每个非树顶点V的一条边(即它与树中的顶点连接起来的权重最小的那条边),因为其他权重较大的边迟早都会失效。
实现过程如下图:
代码实现:
/*** prim的即时实现*/
public class PrimMST {private Edge[] edgeTo; //点离生成树最近的边private int[] distTo; //点到生成树的距离private boolean[] visited;private IndexMinPQ<Integer> pq; //索引优先队列,关联顶点与distTopublic PrimMST(WeightedGraph wg) {//初始化edgeTo = new Edge[wg.getVertexsNum()];distTo = new int[wg.getVertexsNum()];visited = new boolean[wg.getVertexsNum()];for(int i=0; i<wg.getVertexsNum(); i++) {distTo[i] = Integer.MAX_VALUE;}pq = new IndexMinPQ<>(wg.getVertexsNum());distTo[0] = 0;pq.insert(0, 0);while(!pq.isEmpty()) {visit(wg, pq.delMin());}}private void visit(WeightedGraph wg, int ver) {visited[ver] = true;for(Edge e : wg.adj(ver)) {int vertex = e.other(ver); //边的另一个点if(visited[vertex])continue;if(e.getWeight() < distTo[vertex]) {edgeTo[vertex] = e; //被覆盖的边失效distTo[vertex] = e.getWeight();if(pq.contains(vertex)) {pq.change(vertex, distTo[vertex]); }else {pq.insert(vertex, distTo[vertex]);}}}}public Iterable<Edge> getMST() {return Arrays.asList(edgeTo);}
}
此方法的时间复杂度为 O(ElogV),空间复杂度为 O(V)。其中,V为顶点个数,E为边数。
可以看出Prim算法的即时实现比延迟实现明显要快,特别是对于稠密矩阵(E>>>V)的情况。
2、Kruskal算法
Kruskal算法的思想是按照边的权重顺序来生成最小生成树,首先将图中所有边加入优先队列,将权重最小的边出队加入最小生成树,保证加入的边不与已经加入的边形成环,直到树中有V-1到边为止。
实现过程如下图:
/*** Kruskal算法的实现*/
public class KruskalMST {private List<Edge> mst; //存储最小生成树的边private MinPQ<Edge> pq; //优先队列private int[] parent; //用来判断边与边是否形成回路public KruskalMST(WeightedGraph wg) {mst = new ArrayList<Edge>();pq = new MinPQ<>(wg.getEdgesNum());parent = new int[wg.getVertexsNum()];for(Edge e : wg.getEdges()) {pq.enQueue(e);}//最小生成树的边最多为V-1个while(!pq.isEmpty() && mst.size() < wg.getVertexsNum() - 1) {Edge e = pq.deQueue();int v = e.either();int n = find(parent, v);int m = find(parent, e.other(v));if(n != m) { //表示此边没有与生成树形成环路parent[n] = m;mst.add(e);}}}//查找连接树的尾部下标private int find(int[] data, int v) {while(parent[v] > 0) {v = parent[v];}return v;}public Iterable<Edge> getMST() {return mst;}
}
Kruskal算法的时间复杂度最坏情况下为O(ElogE)。空间复杂度为O(E)。
对比Prim算法和Kruskal算法,Kruskal算法主要根据边来生成树,边数少时效率比较高,适合稀疏图;而Prim算法对边数多的稠密图效果更好一些。
五、最短路径
最短路径指两顶点之间经过的边上权值之和最少的路径,并且称路径上的第一个顶点为源点,最后一个顶点为终点。
为了操作方便,首先使用面向对象的方法,来实现一个加权的有向图,其代码如下:
/*** 有向边*/
public class Edge{private final int from;private final int to;private final int weight;public Edge(int from, int to, int weight) {super();this.from = from;this.to = to;this.weight = weight;}public int getFrom() {return from;}public int getTo() {return to;}public int getWeight() {return weight;}
}//带权有向图的实现
public class WeightedDigraph {private final int vertexsNum;private final int edgesNum;private List<Edge>[] adj; //邻接表public WeightedDigraph(int[][] data, int vertexsNum) {this.vertexsNum = vertexsNum;this.edgesNum = data.length;adj = (List<Edge>[]) new ArrayList[vertexsNum];for(int i=0; i<vertexsNum; i++) {adj[i] = new ArrayList<>();}for (int i = 0; i < data.length; i++) {Edge edge = new Edge(data[i][0],data[i][1],data[i][2]);int v = edge.getFrom();adj[v].add(edge);}}public Iterable<Edge> adj(int vertex) {return adj[vertex];}public int getVertexsNum() {return vertexsNum;}public int getEdgesNum() {return edgesNum;}//有向图中所有的边public Iterable<Edge> getEdges() {List<Edge> edges = new ArrayList<>();for(List<Edge> list : adj) {for(Edge e : list) {edges.add(e);}}return edges;}
}
顶点到源点s的最短路径,我们使用一个用顶点索引的Edge数组(edgeTo[])来存储,使用数组distTo[]来存储最短路径树(包含了源点S到所有可达顶点的最短路径)。
边的松弛操作:
边的松弛过程如下图:
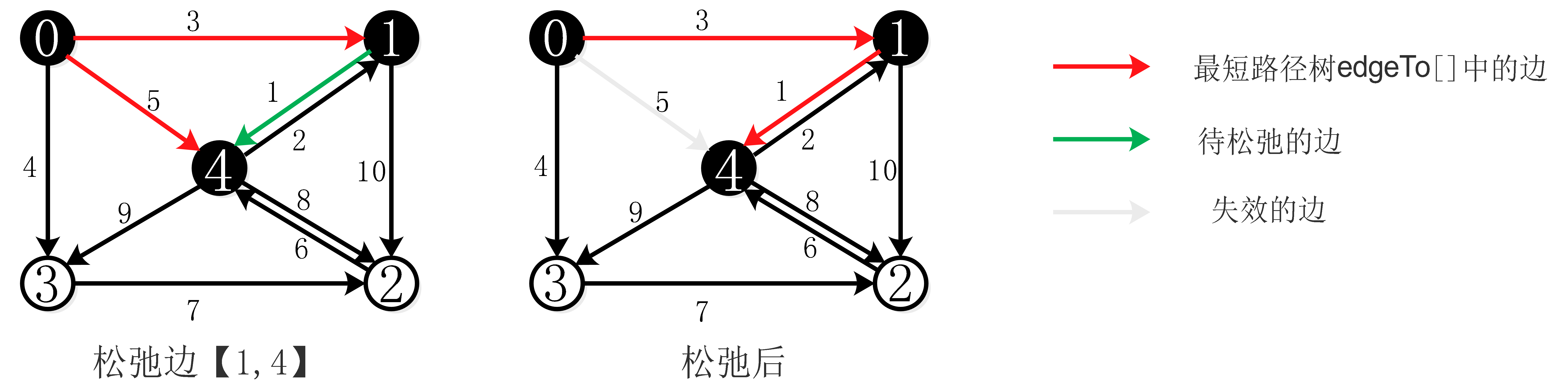
松弛边【1,4】就是检查顶点0到4的最短路径是否是先从顶点0到1,然后在由顶点1到4。如果是则【0,4】边失效,将【1,4】加入最短路径树。
代码:
private void relax(WeightedDigraph wd,Edge e) {int v = e.getFrom();int w = e.getTo();if(distTo[w] > distTo[v] + e.getWeight()) {distTo[w] = distTo[v] + e.getWeight();edgeTo[w] = e;}
}
顶点的松弛操作:
顶点的松弛就是松弛顶点的所有邻接边,这里就不给出过程了,实现代码在Dijkstra实现中。
1、Dijkstra算法
算的的实现过程:
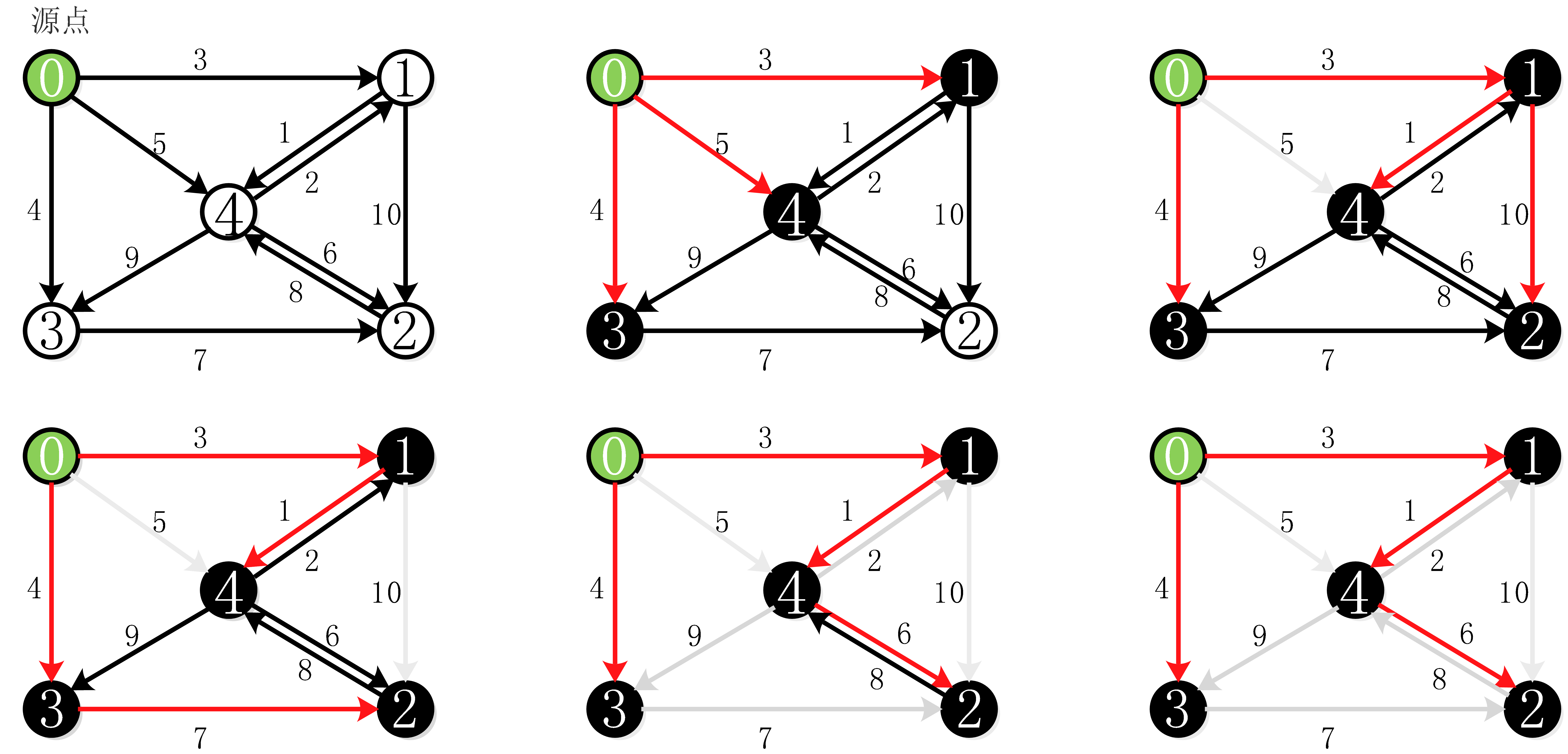
Dijkstra算法的代码实现:
//Dijkstra算法的实现
public class Dijkstra {private Edge[] edgeTo; //最短路径树private int[] distTo; //存储每个顶点到源点的距离//索引优先队列,建立distTo和顶点索引,distTo越小,优先级越高private IndexMinPQ<Integer> pq; public Dijkstra(WeightedDigraph wd, int s) {edgeTo = new Edge[wd.getVertexsNum()];distTo = new int[wd.getVertexsNum()];pq = new IndexMinPQ<>(wd.getVertexsNum());for(int i=0; i<wd.getVertexsNum(); i++) {distTo[i] = Integer.MAX_VALUE;}distTo[s] = 0; //源点s的distTo为0pq.insert(s, 0);while(pq.isEmpty()) {relax(wd, pq.delMin());}}//顶点的松弛private void relax(WeightedDigraph wd, int ver) {for(Edge e : wd.adj(ver)) {int v = e.getTo();if(distTo[v] > distTo[ver] + e.getWeight()) {distTo[v] = distTo[ver] + e.getWeight();edgeTo[v] = e;if(pq.contains(v)) {pq.change(v, distTo[v]);}else {pq.insert(v, distTo[v]);}}}}
}
Dijkstra算法的局限性:图中边的权重必须为正,但可以是有环图。时间复杂度为O(ElogV),空间复杂度O(V)。
相关文章:

数据结构与算法(六):图结构
图是一种比线性表和树更复杂的数据结构,在图中,结点之间的关系是任意的,任意两个数据元素之间都可能相关。图是一种多对多的数据结构。 一、基本概念 图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成&#x…...

Kubernetes07:Service
Kubernetes07:Service 1、service存在的意义 因为Pod的IP是不断变化的,所以需要注册service防止pod失联 1)为了防止Pod失联(服务发现) 2、定义一组Pod访问策略(负载均衡) 2、Pod和Service的关系-------通…...

Qt音视频开发18-不同视频打开无缝切换
一、前言 在轮询视频的时候,通常都是需要将之前的视频全部关闭,然后打开下一组视频,在这个切换的过程中,如果是按照常规的做法,比如先关闭再打开新的视频,肯定会出现空白黑屏之类的过度空白区间࿰…...
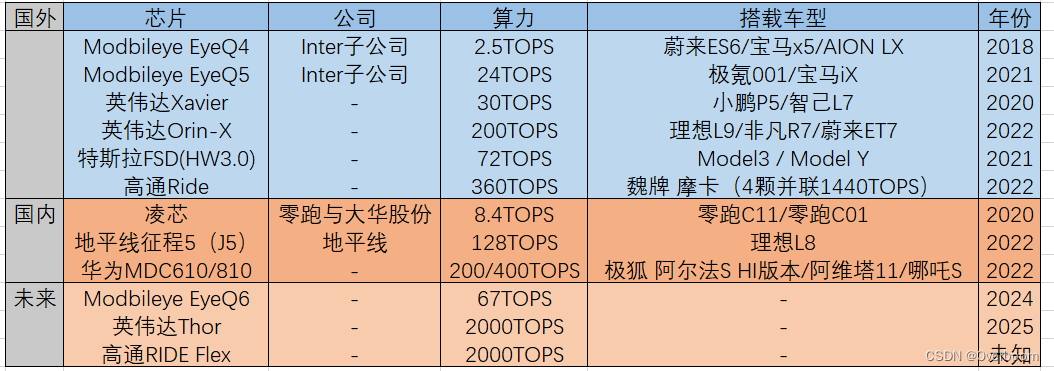
智能驾驶词典 --- 自动驾驶芯片梳理
0 前言 与智能驾驶相关的芯片主要分为自动驾驶芯片(边缘端)和智能座舱芯片两大类,另外衍生的相关芯片种类还有计算集群芯片(云端), 1 自动驾驶芯片梳理 目前业内具有代表性的智驾芯片产品梳理如下。 1…...

在NVIDIA NX 配置OpenCV多版本冲突和解决的总结
Nvidia Jetson NX 环境 直接刷JetPack5.1的镜像,会得到如下环境 Ubuntu20.04cuda11.4TensorRT8.4cudnn8.4opencv4.5.4 而且这些源一般是从nv-xxxx等源下载的,打开软件Software&Update可以更该是否从这些源安装deb包。同时意味着,我们…...
记录pytorch安装 windows10 64位--(可选)安装paddleseg
安装完paddlepaddle之后,就可以安装paddleseg了。一、安装Git可以参考这个网址:https://blog.csdn.net/u010348546/article/details/124280236windows下安装git和gitbash安装教程二、安装paddleseghttps://github.com/PaddlePaddle/PaddleSeg记得翻墙啊这…...
UWB到底是什么技术?
什么是空间感知能力 所谓的空间感知能力,就是感知方位的能力。更直接一点,就是定位能力。说白了,利用UWB技术,手机和智能设备可以更精准地实现室内定位,不仅可以感知自己的位置,还可以感知周边其它手机或设…...

NCRE计算机等级考试Python真题(八)
第八套试题1、数据库设计中反映用户对数据要求的模式是___________。A.概念模式B.内模式C.设计模式D.外模式正确答案: D2、一个工作人员可使用多台计算机,而一台计算机被多个人使用,则实体工作人员与实体计算机之间的联系是___________。A.多…...
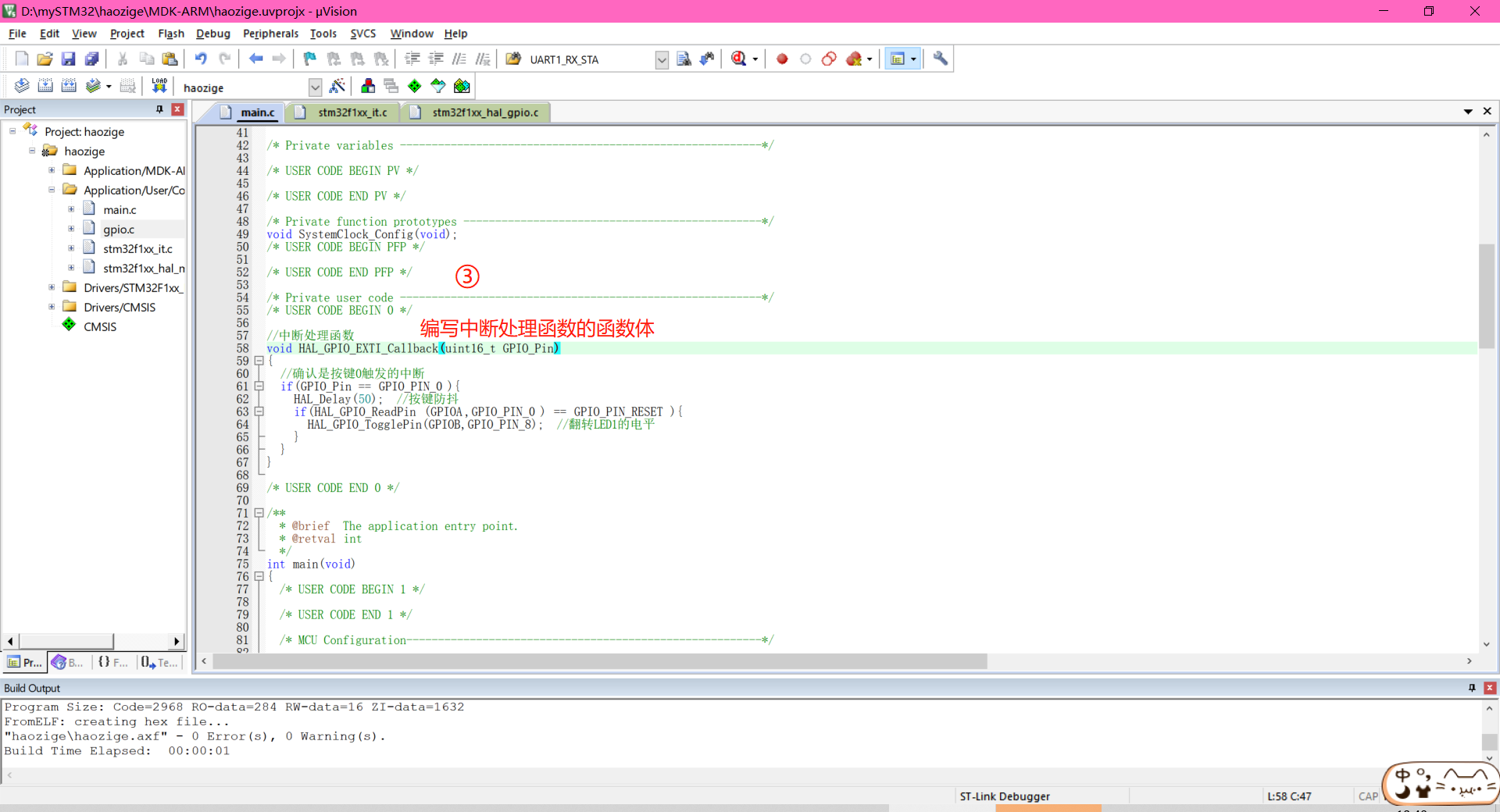
STM32之中断和事件
中断和事件什么是中断当CPU正在执行程序时,由于发生了某种事件,要求CPU暂时中断当前的程序执行,转而去处理这个随机事件,处理完以后,再回到原来被中断的地方,继续原来的程序执行,这样的过程称为…...

MySQL索引类型(type)分析
type索引类型 system > const > eq_ref > ref > range > index > all 优化级别从左往右递减,没有索引的⼀般为’all’。推荐优化目标:至少要达到 range 级别, 要求是 ref 级别, 如果可以是 const 最好ÿ…...
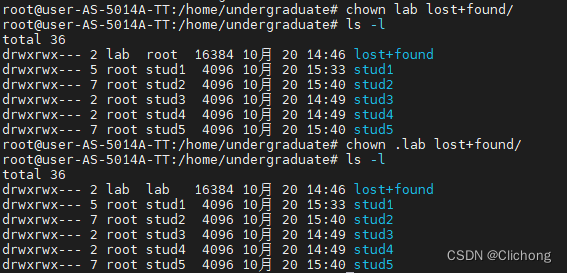
Linux | 2. 用户管理
如有错误,恳请指出。 1. 设置文件权限 权限设置如下: root表示文件所有者,stud1表示文件所属组。其他用户无法访问。更改指令是chown。 更改目录文件所属组:chown .lab lossfound/更改目录文件所有者:chown lab loss…...
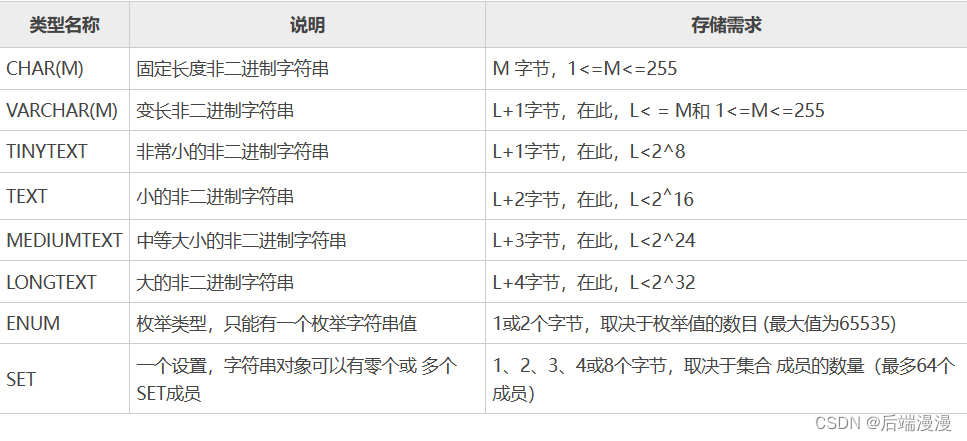
【MySQL之SQL语法篇】系统学习MySQL,从应用SQL语法到底层知识讲解,这将是你见过最完成的知识体系
文章目录一、数据管理技术的三个阶段二、SQL语句学习1. DCL数据控制语言1.1 创建用户1.2 修改用户名1.3 修改密码1.4 删除用户1.5 授权1.6 查看权限1.7 回收权限2. DDL数据定义语言2.1 操作数据库2.2 操作数据表2.3 操作数据3. DQL数据查询语言基本语法3.1 单表查询3.1.1选择表…...
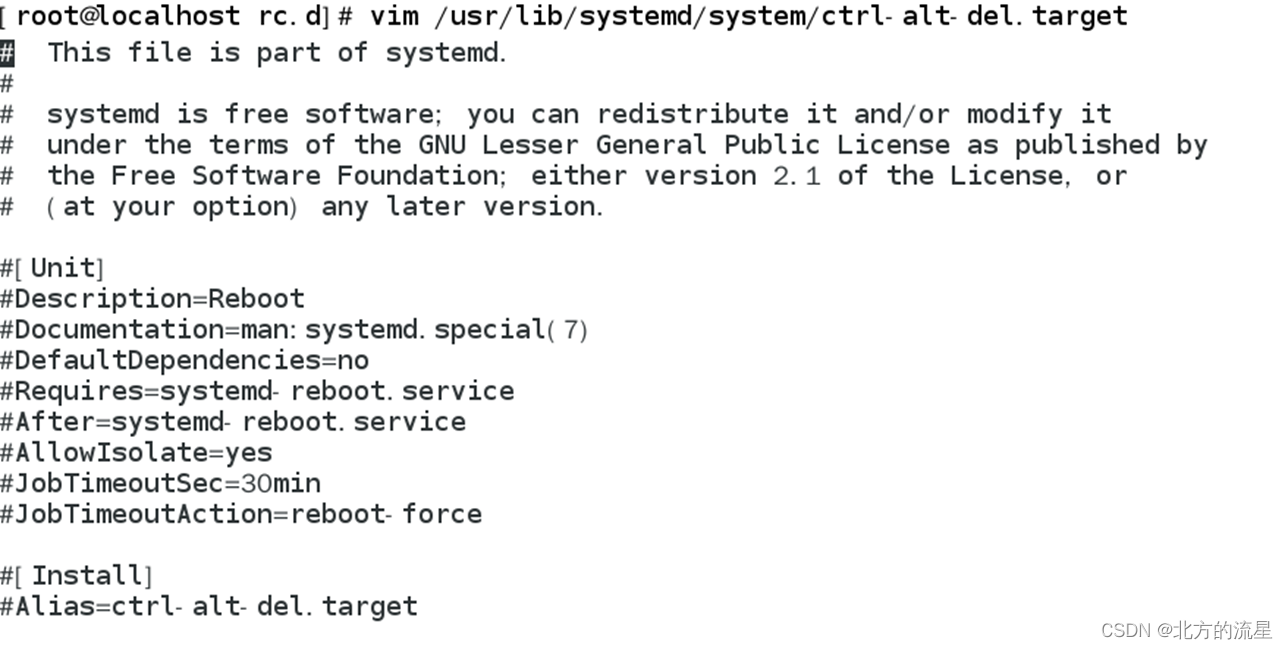
CentOS8基础篇7:Linux系统启动配置
一、Linux系统的启动过程 Linux的启动过程大体分为五个阶段: 1.计算机主机加电后,CPU初始化自身,接着在硬件固定位置执行一条指令。这条指令跳转到BIOS,BIOS找到启动设备并获取MBR,该MBR指向LILO或GRUB。 …...
vue中的$forceUpdate()、$set()
$forceUpdate() 迫使vue实例重新(rander)渲染虚拟dom,注意并不是重新加载组件。 结合vue的生命周期,调用 $forceupdate 后只会触发beforeupdate和updated这两个钩子函数,不会触发其他的钩子函数。它仅仅影响实例本身和…...
记住这3点,有效提高江苏专转本上岸率
记住这3点,有效提高上岸率 我们都知道,在江苏统招专转本考试中想岸并不是一件容易的事情。考生能否顺利上岸,往往受多方面因素影响,这其中包括:个人基础、学习方式、信息搜索能力。 如何提高自己的专转本上岸几率&…...

【经验总结】10年的嵌入式开发老手,到底是如何快速学习和使用RT-Thread的?(文末赠书5本)
【经验总结】一位近10年的嵌入式开发老手,到底是如何快速学习和使用RT-Thread的? RT-Thread绝对可以称得上国内优秀且排名靠前的操作系统,在嵌入式IoT领域一直享有盛名。近些年,物联网产业的大热,更是直接将RT-Thread这…...

人大金仓和达梦的空间数据能力对比
一、总得来说: 人大金仓底层更解决于pg数据库, 人大金仓的空间能力基于postgis能力来实现,能力挺强大的. 细节上人大金仓的架构上也对空间的支持框架做的比达梦更加完善。例如数据库的集群能力,并行计算能力,空间数据…...

探析集团企业 1+N 模式,重新定义集团型CRM
目录 一、客户经营、运营监控 二、流程驱动、业务成长 三、规则规范 业务治理 什么是集团型CRM【1N】?本文中我们可以把集团看作为“1”,其他分公司或组织看作为“N”。本篇我们主要分析集团CRM业务定位。 我们从企业集团总部的职能定位确定集团CRM…...
卡特兰数
文章目录1、简介1.1 何为卡特兰数1.2 卡特兰数的通项公式2、应用2.1 题目1:括号合法题目描述思路分析2.2 题目2:进出栈的方式2.2.1 题目描述2.2.2 思路分析2.3 题目3:合法的序列2.3.1 题目描述2.3.2 思路分析2.3.3 代码实现2.4 题目4…...
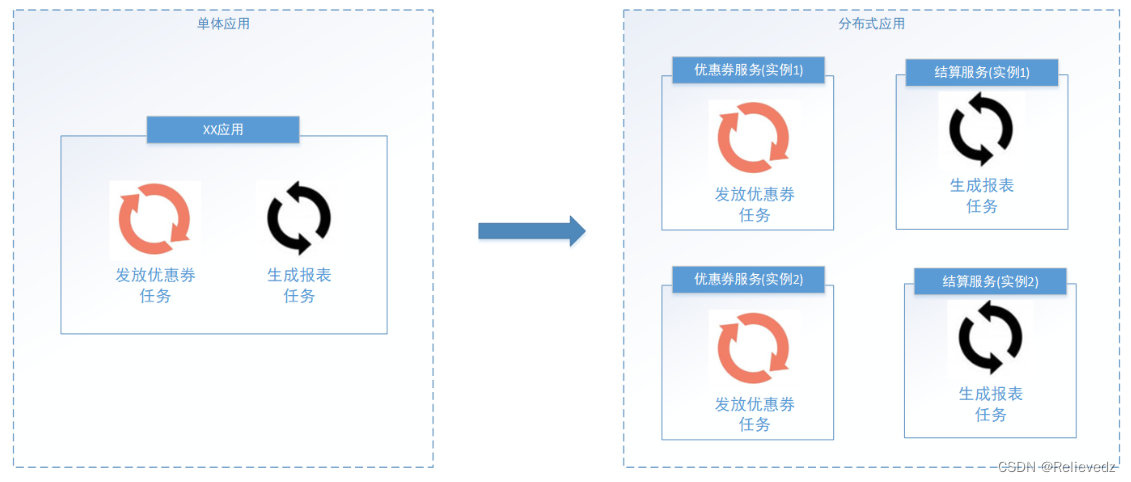
分布式任务处理
分布式任务处理 1. 什么是分布式任务调度 视频上传成功需要对视频的格式进行处理,如何用Java程序对视频进行处理呢?这里有一个关键的需求就是当视频比较多的时候我们如何可以高效处理。 如何去高效处理一批任务呢? 1、多线程 多线程是充…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
