vue中的$forceUpdate()、$set()
$forceUpdate()
迫使vue实例重新(rander)渲染虚拟dom,注意并不是重新加载组件。
结合vue的生命周期,调用 $forceupdate 后只会触发beforeupdate和updated这两个钩子函数,不会触发其他的钩子函数。它仅仅影响实例本身和插入插槽内容的子组件,而不是所有子组件
页面传的数值动态改变,接口接受的参数也就动态更改,但接收的数据有时候不会及时不变,通过this.$forceUpdate()页面强制刷新来解决这个问题
首先我们知道在vue中,数据的绑定都不用我们操心,例如在data中有一个msg的变量,你修改它,那么在页面上,msg的内容就会自动发生变化。但是如果对于一个复杂的对象,例如一个对象数组,你直接去给数组上某一个元素增加属性,或者直接把数组的length变成0,vue就无法知道发生了改变。
change: function(index) {//增加性别属性this.list[index].sex = '男';
},
clear: function() {//清空数组this.list.length = 0;
}
使用$forceUpdate()
change: function(index) {this.list[index].sex = '男';this.$forceUpdate();
},
clear: function() {this.list.length = 0;this.$forceUpdate();
}
使用$set
change: function(index) {//增加性别属性this.$set(this.list[index],'sex','男')
},
clear: function() {//清空数组this.list=[];
}
注意:但是$forceUpdate()这种做法并不推荐,官方说如果你现在的场景需要用$forceupdate方法,那么99%是你的操作有问题,比如data里不显示声明对象的属性,之后添加属性时正确的做法时用 vm.$set() 方法,所以$forceupdate请慎用。
相关问题
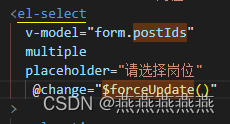
在使用Element-Ui的select组件时,在设置了初始值后,重新选择select下拉后出现了下拉无法回显的情况,但是在进行了表单的其他项的操作后,select的选择就马上回显了
经过排查也不是下拉框绑定的值有问题
最后发现是data数据的层级过深,导致无法响应式显示
解决方法一:
this.$set(this.form, 'postIds', res.postIds)
解决方法二:
在对应的select组件增加@change事件,事件对应为$forceUpdate()即可
相关文章:

vue中的$forceUpdate()、$set()
$forceUpdate() 迫使vue实例重新(rander)渲染虚拟dom,注意并不是重新加载组件。 结合vue的生命周期,调用 $forceupdate 后只会触发beforeupdate和updated这两个钩子函数,不会触发其他的钩子函数。它仅仅影响实例本身和…...
记住这3点,有效提高江苏专转本上岸率
记住这3点,有效提高上岸率 我们都知道,在江苏统招专转本考试中想岸并不是一件容易的事情。考生能否顺利上岸,往往受多方面因素影响,这其中包括:个人基础、学习方式、信息搜索能力。 如何提高自己的专转本上岸几率&…...

【经验总结】10年的嵌入式开发老手,到底是如何快速学习和使用RT-Thread的?(文末赠书5本)
【经验总结】一位近10年的嵌入式开发老手,到底是如何快速学习和使用RT-Thread的? RT-Thread绝对可以称得上国内优秀且排名靠前的操作系统,在嵌入式IoT领域一直享有盛名。近些年,物联网产业的大热,更是直接将RT-Thread这…...

人大金仓和达梦的空间数据能力对比
一、总得来说: 人大金仓底层更解决于pg数据库, 人大金仓的空间能力基于postgis能力来实现,能力挺强大的. 细节上人大金仓的架构上也对空间的支持框架做的比达梦更加完善。例如数据库的集群能力,并行计算能力,空间数据…...

探析集团企业 1+N 模式,重新定义集团型CRM
目录 一、客户经营、运营监控 二、流程驱动、业务成长 三、规则规范 业务治理 什么是集团型CRM【1N】?本文中我们可以把集团看作为“1”,其他分公司或组织看作为“N”。本篇我们主要分析集团CRM业务定位。 我们从企业集团总部的职能定位确定集团CRM…...
卡特兰数
文章目录1、简介1.1 何为卡特兰数1.2 卡特兰数的通项公式2、应用2.1 题目1:括号合法题目描述思路分析2.2 题目2:进出栈的方式2.2.1 题目描述2.2.2 思路分析2.3 题目3:合法的序列2.3.1 题目描述2.3.2 思路分析2.3.3 代码实现2.4 题目4…...
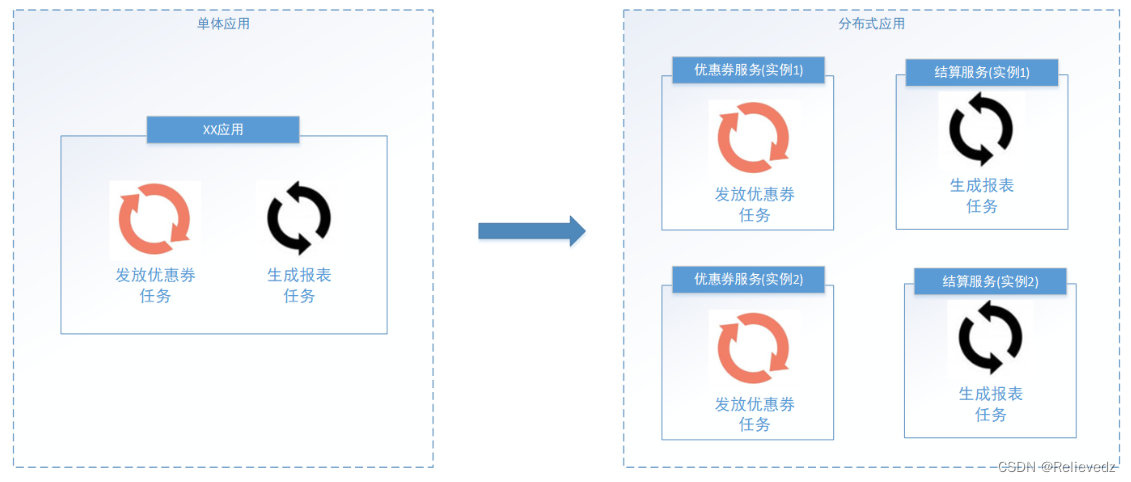
分布式任务处理
分布式任务处理 1. 什么是分布式任务调度 视频上传成功需要对视频的格式进行处理,如何用Java程序对视频进行处理呢?这里有一个关键的需求就是当视频比较多的时候我们如何可以高效处理。 如何去高效处理一批任务呢? 1、多线程 多线程是充…...

Linux 命令复习
常用命令 1、目录操作 cd 切换目录 cd / 切换到根目录 cd ~ 回到个人用户的主目录 ls 查看当前目录下所有文件的详细信息 list的意思 ll 查看当前目录下所有文件的详细信息 pwd 显示当前目录的全路径 . …...
)
leetcode 困难 —— 天际线问题(优先队列)
(思路感觉挺明显的,就是一些特殊情况得考虑清楚) 题目: 城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度,请返回 由这些建筑物形成的 天际线 。 每个建筑物的几何信息…...
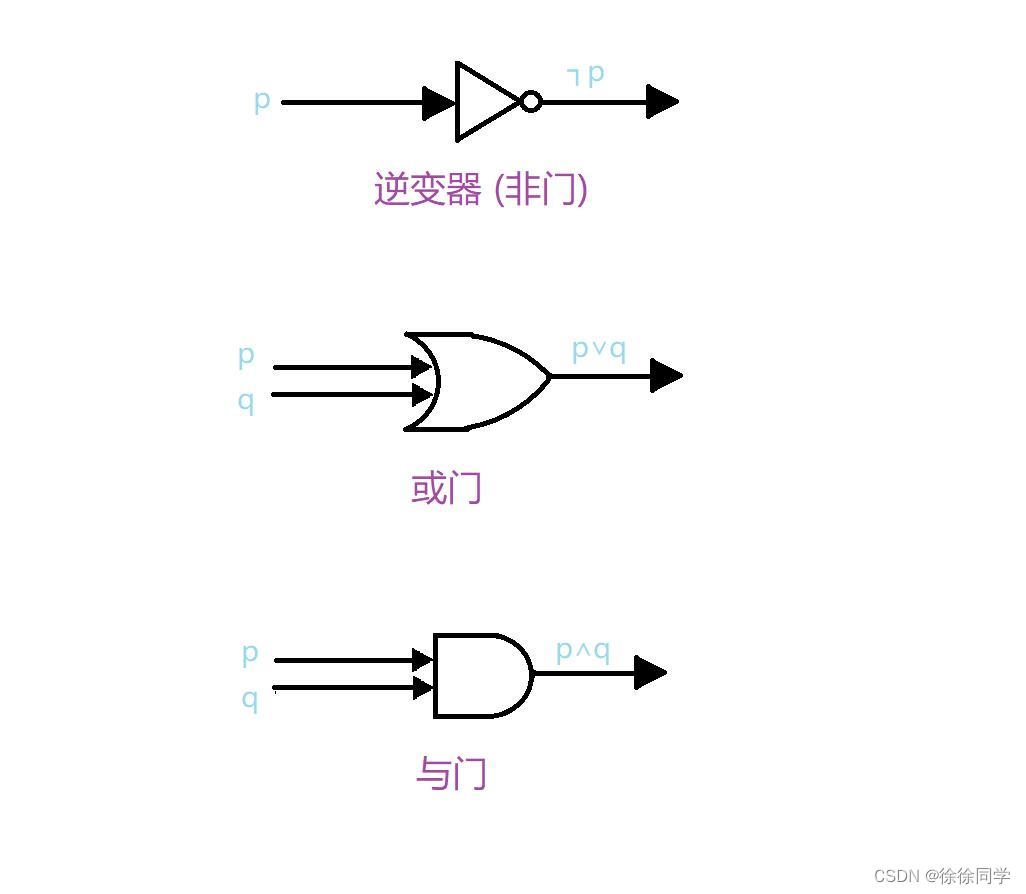
离散数学笔记_第一章:逻辑和证明(2 )
1.2 命题逻辑的应用1.2.1 语句翻译 1.2.2 系统规范说明 1.2.3 布尔搜索 1.2.4 逻辑谜题泥巴孩子谜题骑士和流氓(考研逻辑题)1.1.2.5 逻辑电路1.2.1 语句翻译 🐳为啥要翻译语句? ➡因语言常常有二义性(有歧义&#x…...

MFCC语音特征值提取算法
博主简介 博主是一名大二学生,主攻人工智能研究。感谢让我们在CSDN相遇,博主致力于在这里分享关于人工智能,c,Python,爬虫等方面知识的分享。 如果有需要的小伙伴可以关注博主,博主会继续更新的,…...

TencentOS3.1编译安装redis6.2.5
下载地址:https://redis.io/download 最近版为7.0.8,本次安装的是6.2.5 软件包解包并进入目录。 redis是c语言编写的,编译需要gcc,按网上资料说默认安装的gcc版本过低(可能是4.8.5),使用rpm …...

AI顶会accepted papers list
为方便相关paper调研,对相关顶会文章列表和下载地址汇总,会议包括:AAAI、ACL、IJCAI、ICLR、COLING、SIGIR、WSDM、WWW、ICML、KDD、NeurIPS、CVPR、ECCV、ACM MM 2023 Accepted papers list 更新于:(2022.11.24&…...
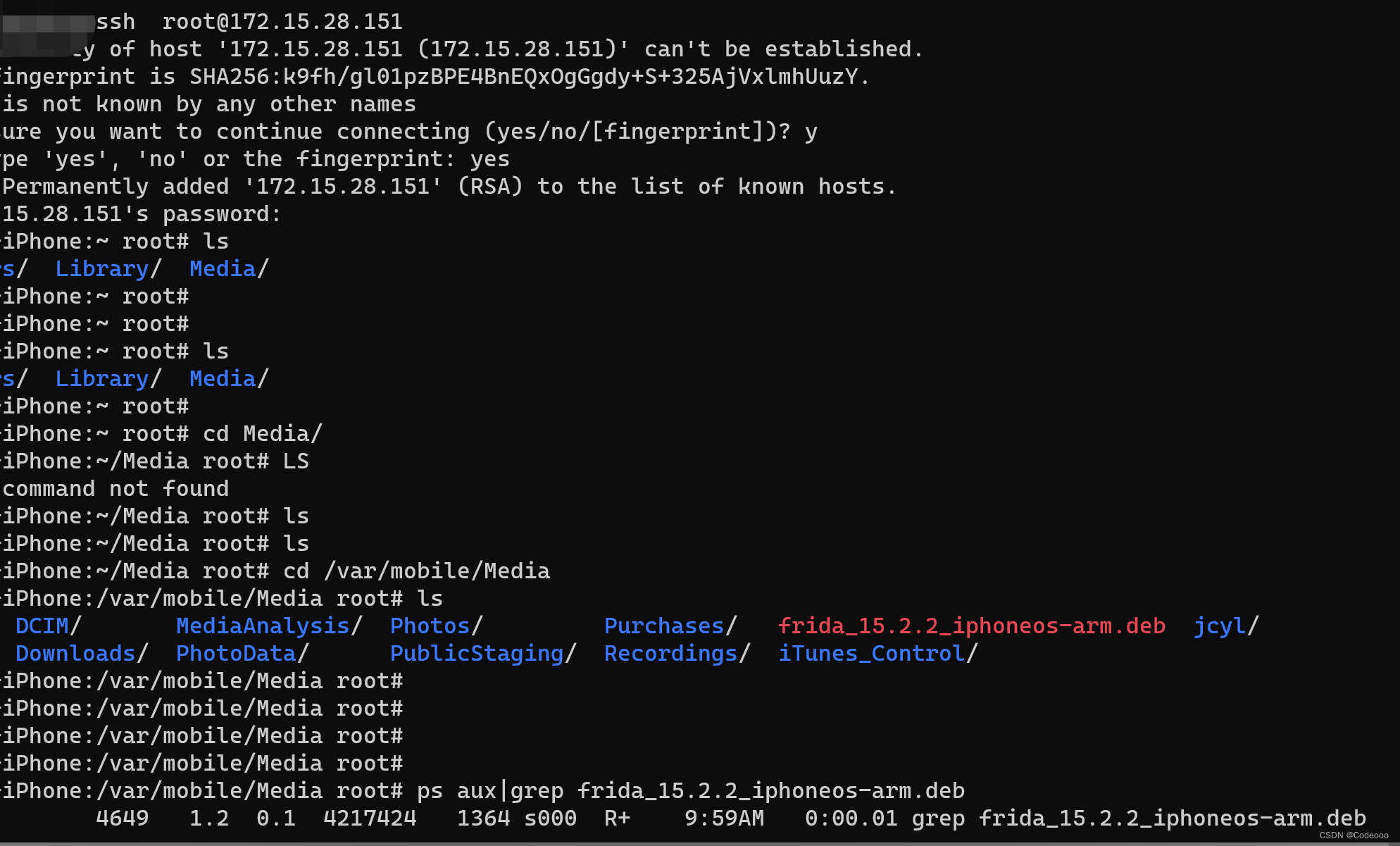
IOS逆向之frida安装
首先手机要越狱,这个就不说了,博主就是咸鱼搞了个160的苹果6, 自己刷到苹果6支持最新的12.5.7版本后越狱; 谁让他低版本,不支持 CrackerXI砸壳呢,当时你要是使用 frida-ios-dump 也是可以的; …...

《金山区提信心扩需求稳增长促发展行动方案》的通知
金发改规〔2023〕1号 各镇政府、街道办事处、园区管委会,区政府各部门、各直属单位: 《金山区提信心扩需求稳增长促发展行动方案》已经区委、区政府同意,现印发给你们,请认真按照执行。 附件:金山区提信心扩需求稳增…...
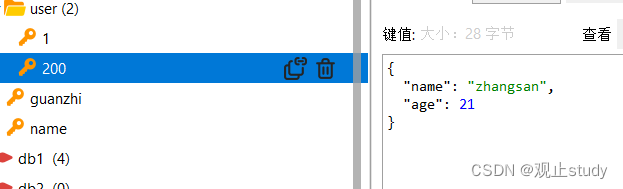
【Redis】Java客户端JedisSpringDataRedis入门(三)
🚗Redis学习第三站~ 🚩起始站:【Redis】概述&环境搭建(一) 🚩本文已收录至专栏:数据库学习之旅 👍希望您能有所收获 在上一篇中我们学习了Redis常见命令的使用,显然,我们不可能一…...

挑选销售自动化工具应该关注什么功能?
销售自动化可以极大地提高你的生产力和效率,每周都为你节省时间。这样,你就可以把更多的时间用于完成交易,而减少用于行政任务的时间。市面上的销售自动化工具有很多,作为一般经验法则,以下是销售自动化工具中需要寻找…...
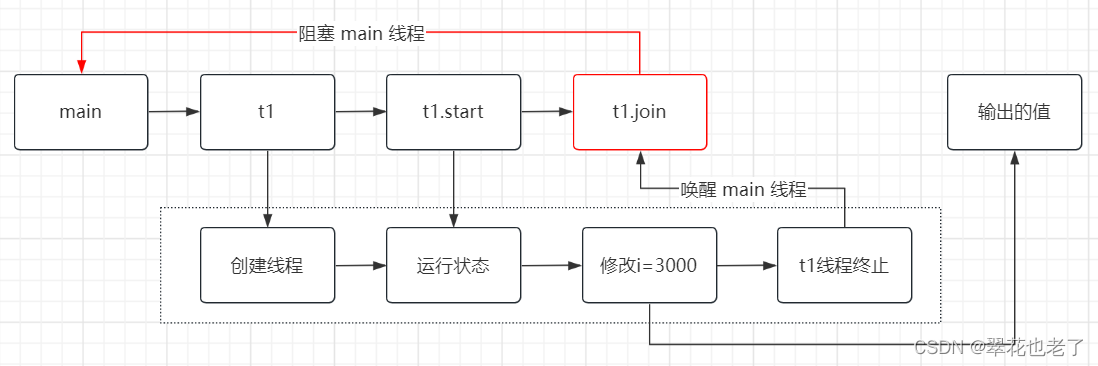
thread.join 是干什么的?原理是什么?
Thread.join 加了join,表示join的线程的修改对于join之外的代码是可见的。 代码示例: public class JoinDemo {private static int i 1000;public static void main(String[] args) {new Thread(()->{i 3000;}).start();System.out.println("…...

论文阅读 | Cross-Attention Transformer for Video Interpolation
前言:ACCV2022wrokshop用transformer做插帧的文章,q,kv,来自不同的图像 代码:【here】 Cross-Attention Transformer for Video Interpolation 引言 传统的插帧方法多用光流,但是光流的局限性在于 第一&…...
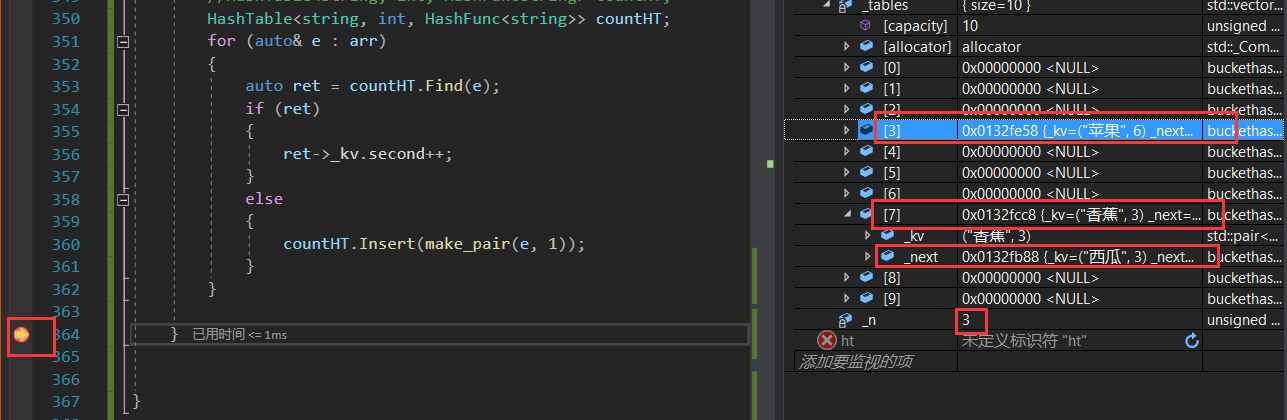
【C++修炼之路】22.哈希
每一个不曾起舞的日子都是对生命的辜负 哈希一.哈希概念及性质1.1 哈希概念1.2 哈希冲突1.3 哈希函数二.哈希冲突解决2.1 闭散列/开放定址法2.2 开散列/哈希桶三.开放定址法代码3.1 插入Insert3.2 查找Find3.3 删除Erase3.4 映射的改良&完整代码四.开散列代码4.1 插入Inser…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
