ACM-蓝桥杯训练第一周
🚀write in front🚀
📝个人主页:认真写博客的夏目浅石.CSDN
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏:ACM周训练题目合集.CSDN
💬总结:希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🖊
✉️为什么我们不知疲倦,因为我们都在做自己所热爱的事 ♐
文章目录
- 前言
- A - [例题]一维前缀和
- B - 二分查找
- C - 一维差分
- D - 快速幂
- E - 质数筛
- F - 最短路径
- G - 结构体排序
- H - sort
- I - 二维前缀和
- 总结

前言
本周进行了一些特别基础的练习来巩固知识,写成博客方便我去复习使用。
A - [例题]一维前缀和

思路:基础的前缀和模板题目,会公式即可。详细可以看我写的博客
#include<iostream>
#include<cstdio>using namespace std;typedef long long ll;
ll n,q;
ll sum[100010];int main()
{cin>>n>>q;for(int i=1;i<=n;i++){ll tmp;cin>>tmp;sum[i]=sum[i-1]+tmp;}while(q--){ll l,r;cin>>l>>r;printf("%lld\n",sum[r]-sum[l-1]);}return 0;
}B - 二分查找

思路:基础的二分模板题目,详细可以看二分模板那篇博客。
#include<iostream>using namespace std;#define N 1000010int a[N],n,m,q;int main()
{cin>>n>>m;for(int i=0;i<n;++i) cin>>a[i];for(int i=0;i<m;++i){cin>>q;int l=0,r=n-1;while(l<r){int mid=(l+r)/2;if(a[mid]>=q) r=mid;else l=mid+1;}if(a[l]!=q) cout <<"-1"<<" ";else cout<<l+1<<" "; }return 0;
}
C - 一维差分

思路:基础差分题目
#include<iostream>
#include<cstring>
#include<cmath>using namespace std;typedef long long ll;
ll n,p,a[5000010];
ll x,y,z,sum,b[5000010],mn=5000010,cnt;int main()
{cin>>n>>p;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=0;i<p;i++){cin>>x>>y>>z;b[x]+=z;b[y+1]-=z;}for(int i=1;i<=n;i++){sum+=b[i];cnt=sum+a[i];mn=min(mn,cnt);}cout<<mn<<endl;return 0;
}
D - 快速幂
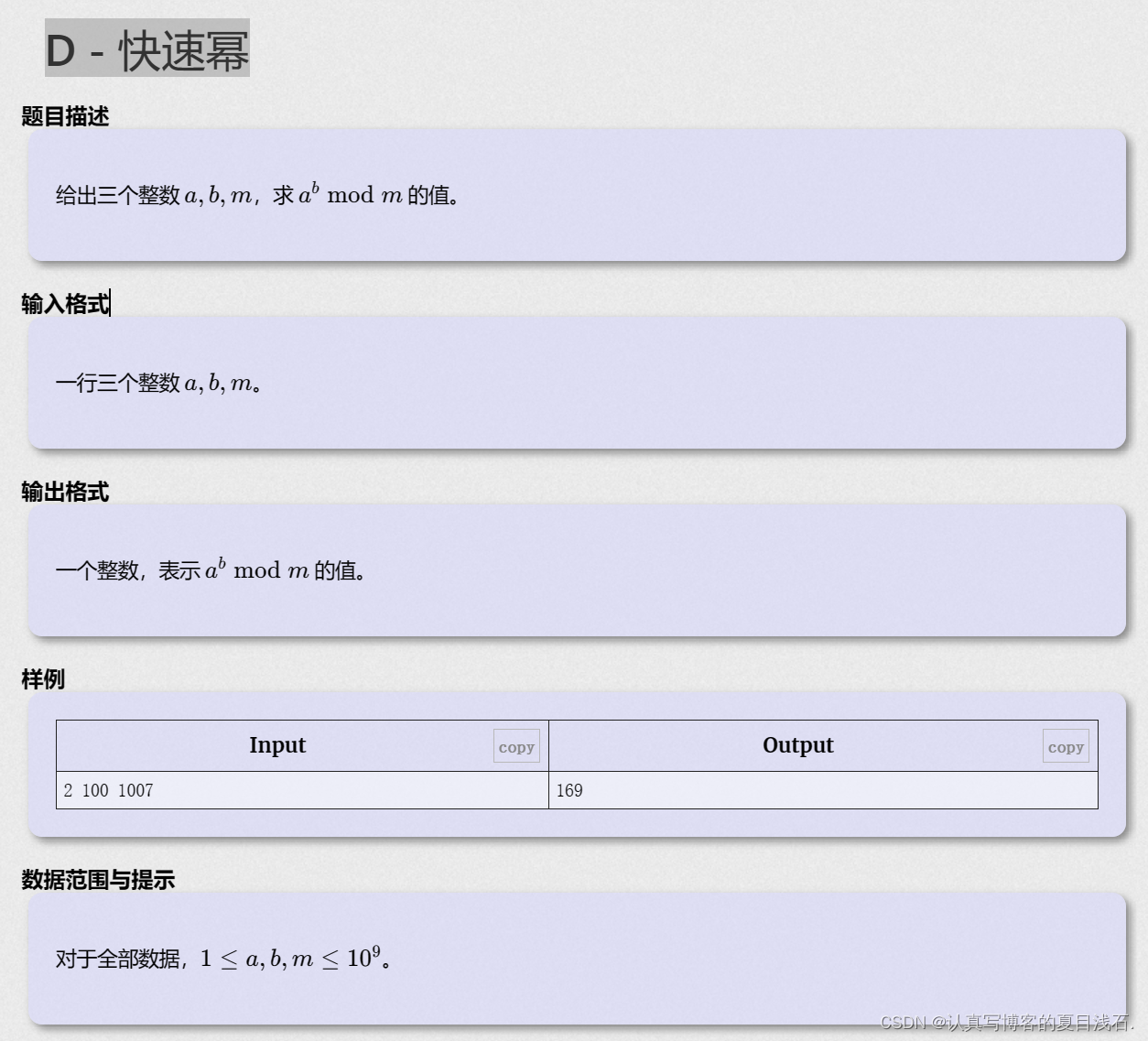
思路:快速幂算法(全网最详细地带你从零开始一步一步优化)(转载)
#include<iostream>
#include<cmath>using namespace std;
typedef long long ll;ll a,b,m;int main()
{cin>>a>>b>>m;ll result=1;while(b){if(b%2==0){b/=2;a=a*a%m;}else{b-=1;result=result*a%m;b/=2;a=a*a%m;}}cout<<result<<endl;return 0;
}
E - 质数筛
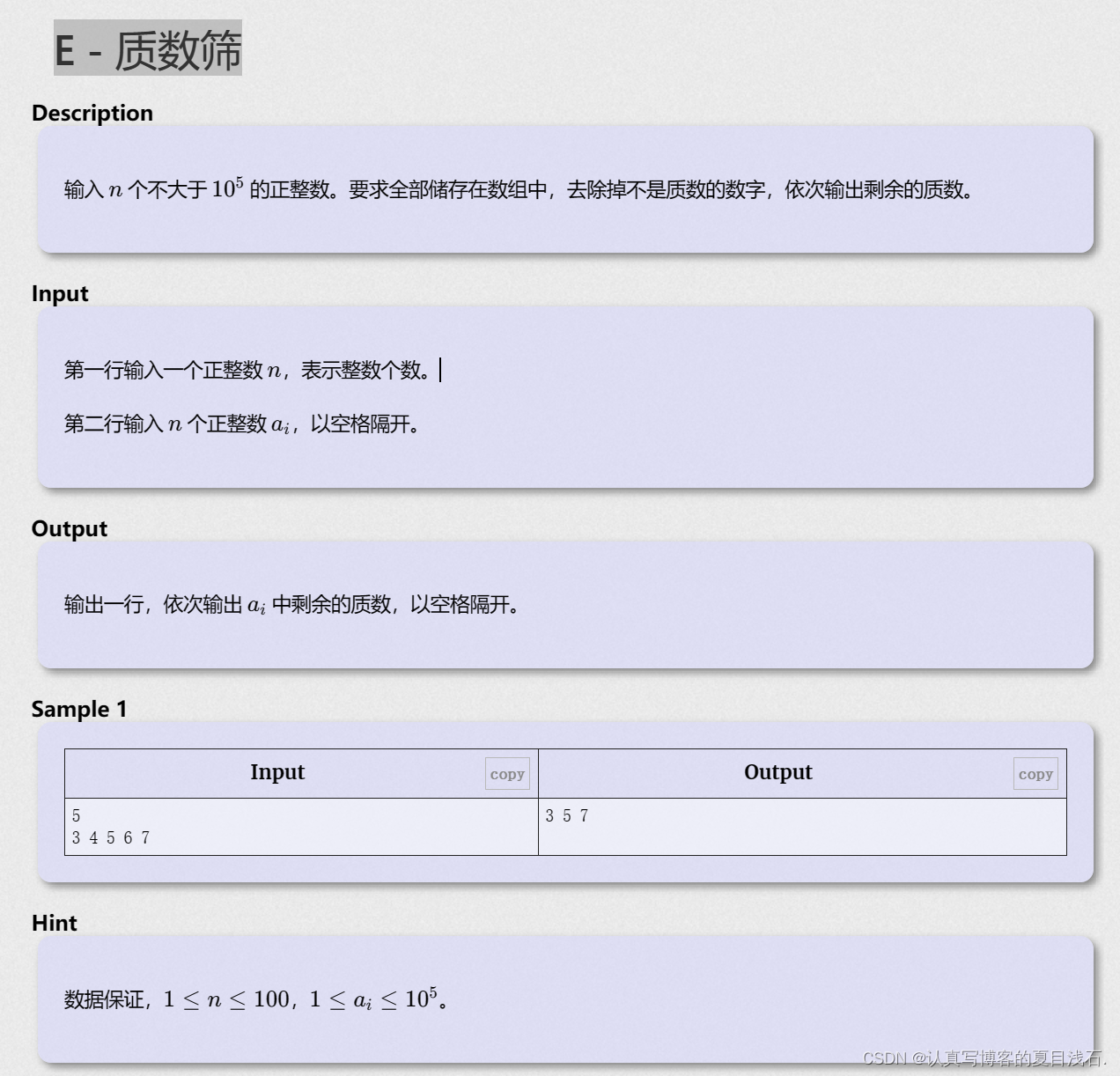
思路:暴力求素数
#include<iostream>
#include<cstring>
#include<cmath>using namespace std;typedef long long ll;int n;
int a[100010];int main()
{cin>>n;for(int i=0;i<n;i++){cin>>a[i];}int j=0;for(int i=0;i<n;i++){for(j=2;j*j<=a[i];j++){if(a[i]%j==0) break;}if(j>a[i]/j&&a[i]>=2) cout<<a[i]<<" ";}return 0;
}
F - 最短路径

思路:最短路的基础模板题目
#include<algorithm>
#include<cstring>
#include<iostream>
using namespace std;int n,m;
int u,v,w;
int g[110][110];
int path[110][110];
const int maxx=99999999;
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j) g[i][j]=0;else g[i][j]=maxx;}}for(int i=1;i<=m;i++){cin>>u>>v>>w;g[u][v]=g[v][u]=w;}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(g[i][j]>g[i][k]+g[k][j]){g[i][j]=g[i][k]+g[k][j];}}}}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){printf("%d ",g[i][j]);}cout<<endl;}return 0;
}
G - 结构体排序

思路:我其实我对于结构体题目不是很熟悉,正好借这一个题目学到很多东西,语法题,重要的在于结构体格式
#include<iostream>
#include<algorithm>
using namespace std;struct Stu
{int math;int chinese;int english;int sum;int id;
}stu[350];int cmp(Stu a,Stu b)
{if (a.sum==b.sum){if (a.chinese==b.chinese)return a.id<b.id;else return a.chinese>b.chinese;}else return a.sum>b.sum;
}int main()
{int n;cin>>n;for(int i=1;i<=n;i++){cin>>stu[i].chinese>>stu[i].math>>stu[i].english;stu[i].id=i;stu[i].sum=stu[i].chinese+stu[i].math+stu[i].english;}sort(stu+1,stu+n+1,cmp);for(int i=1;i<=5;i++){cout<<stu[i].id<<" "<<stu[i].sum<<endl;}return 0;
}
H - sort
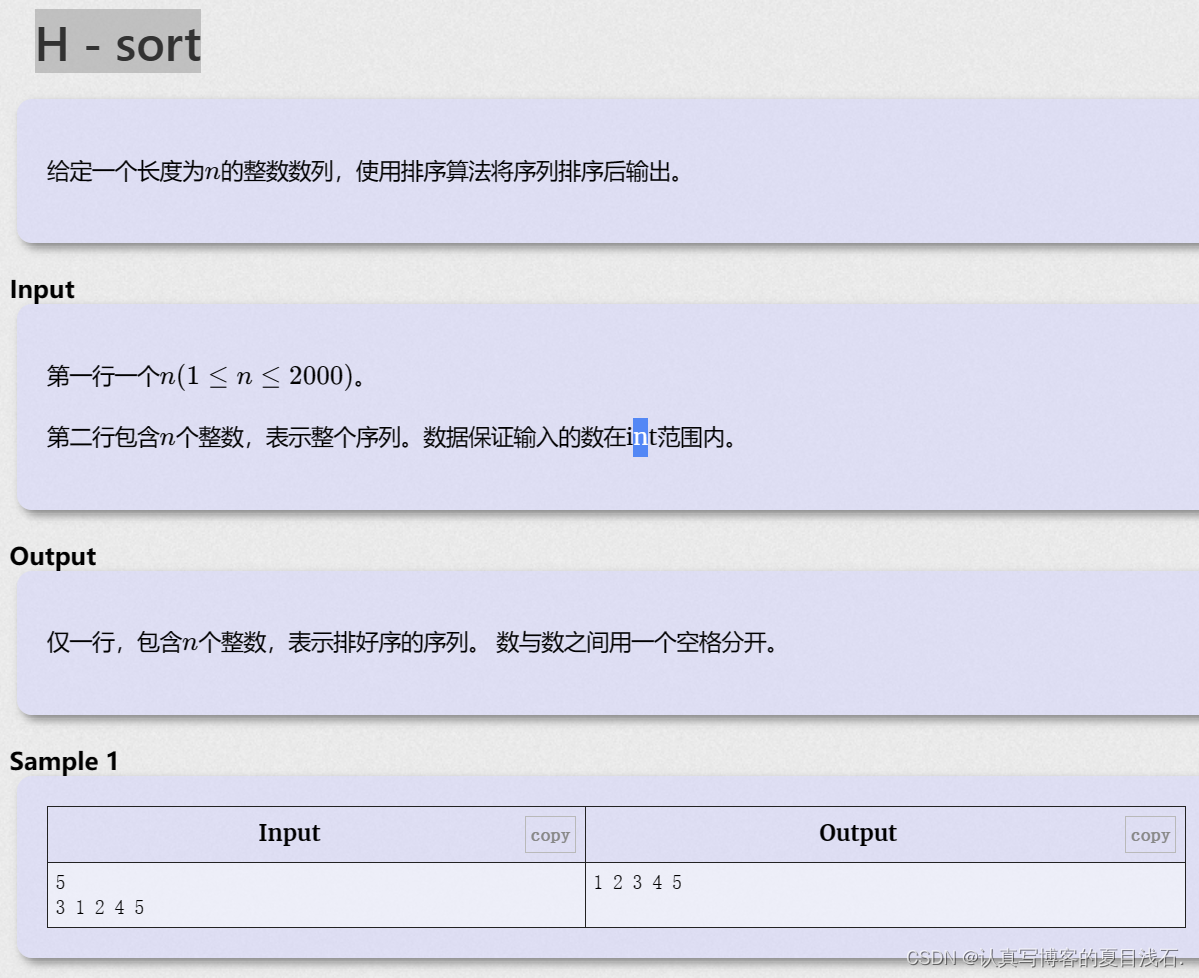
#include<algorithm>#include<iostream>
using namespace std;int main()
{int n;cin>>n;int arr[100010];for(int i=0;i<n;i++){cin>>arr[i];}sort(arr,arr+n);for(int i=0;i<n;i++) cout<<arr[i]<<" ";cout<<endl;return 0;
}I - 二维前缀和
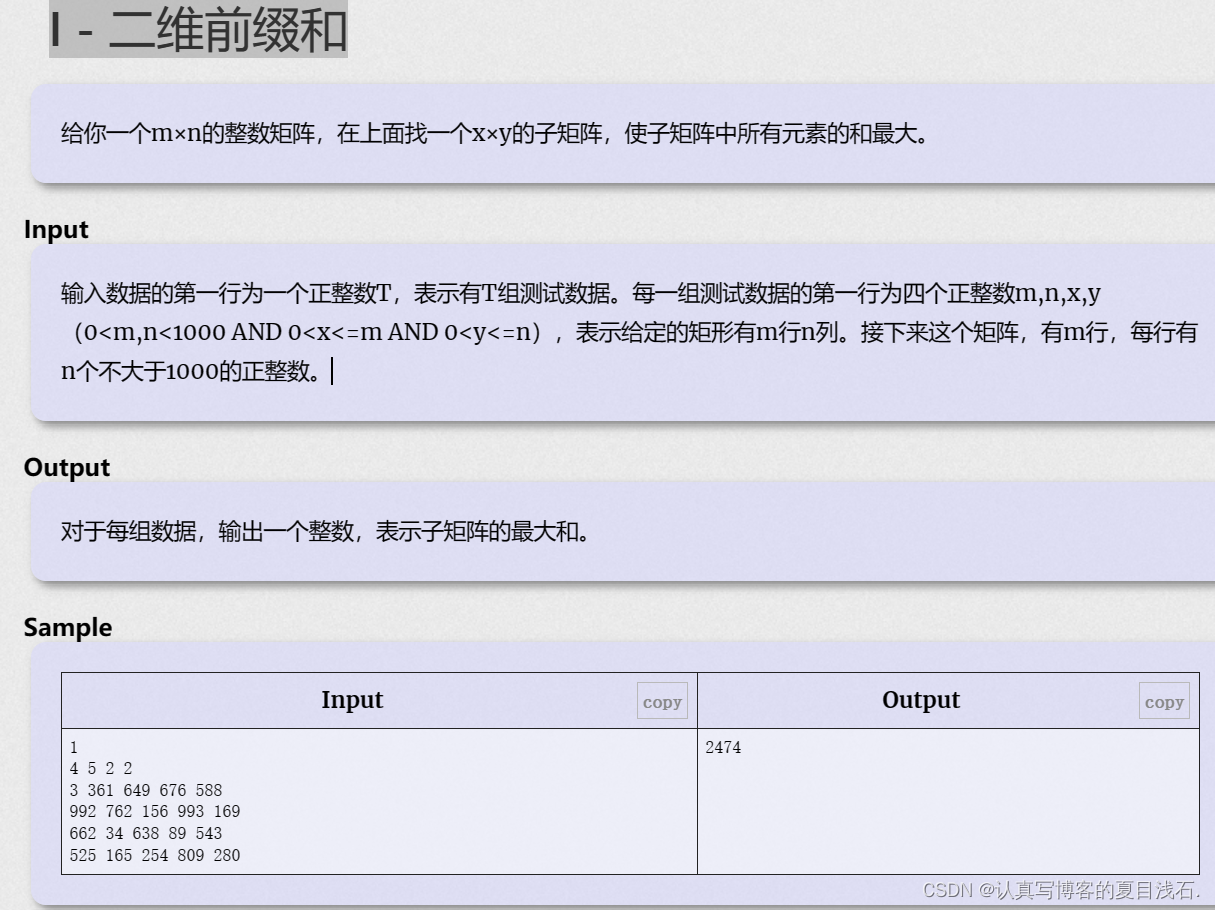
思路:二维前缀和公式: g[i][j]+=g[i-1][j]+g[i][j-1]-g[i-1][j-1];
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>using namespace std;int g[1010][1010];
int T,n,m,x,y;int main()
{cin>>T;while(T--){memset(g,0,sizeof(g));int res=0;cin>>n>>m>>x>>y;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>g[i][j];g[i][j]+=g[i-1][j]+g[i][j-1]-g[i-1][j-1];if(i>=x&&j>=y){res=max(g[i][j]-g[i-x][j]-g[i][j-y]+g[i-x][j-y],res);}}}cout<<res<<endl;}return 0;
}
总结
本周复习了基础的模板题目,重在查漏补缺。
复习:前缀和,二维前缀和,差分,二分查找,sort排序,质数筛,结构体排序
学习:最短路问题,快速幂
我需要加强学习的:二维前缀和,结构体排序,质数筛的埃式筛选法。
相关文章:

ACM-蓝桥杯训练第一周
🚀write in front🚀 📝个人主页:认真写博客的夏目浅石.CSDN 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝 📣系列专栏:ACM周训练题目合集.CSDN 💬总结:…...

python基础—字符串操作
(1)字符串: Python内置了一系列的数据类型,其中最主要的内置类型是数值类型、文本序列(字符串)类型、序列(列表、元组和range)类型、集合类型、映射(字典)类型…...

【Spring】通过JdbcTemplate实现CRUD操作
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 通过JdbcTemplate实现 增删查改一、添加相关依…...

实战|掌握Linux内存监视:free命令详解与使用技巧
文章目录前言一. free命令介绍二. 语法格式及常用选项三. 参考案例3.1 查看free相关的信息3.2 以MB的形式显示内存的使用情况3.3 以总和的形式显示内存的使用情况3.4 周期性的查询内存的使用情况3.5 以更人性化的形式来查看内存的结果输出四. free在脚本中的应用总结前言 大家…...

嵌入式入门必看!调试工具安装——基于 AM64x核心板
本章节内容是为评估板串口安装USB转串口驱动程序。驱动适用于CH340、CH341等USB转串口芯片。 USB转串口驱动安装 适用安装环境:Windows 7 64bit、Windows 10 64bit。 本文测试板卡为创龙科技SOM-TL64x核心板,它是一款基于TI Sitara系列AM64x双核ARM Cortex-A53 + 单/四核Cort…...

JAVA开发(java类加载过程)
1、java语言的平台无关性。 因为java语言可以跑在java虚拟机上,所以只要能装java虚拟机的地方就能跑java程序。java语言以后缀名 .java为文件扩展名。通过java编译器javac编译成字节码文件.class 。java字节码文件通过java虚拟机解析运行。所以java语言可以说是编译…...
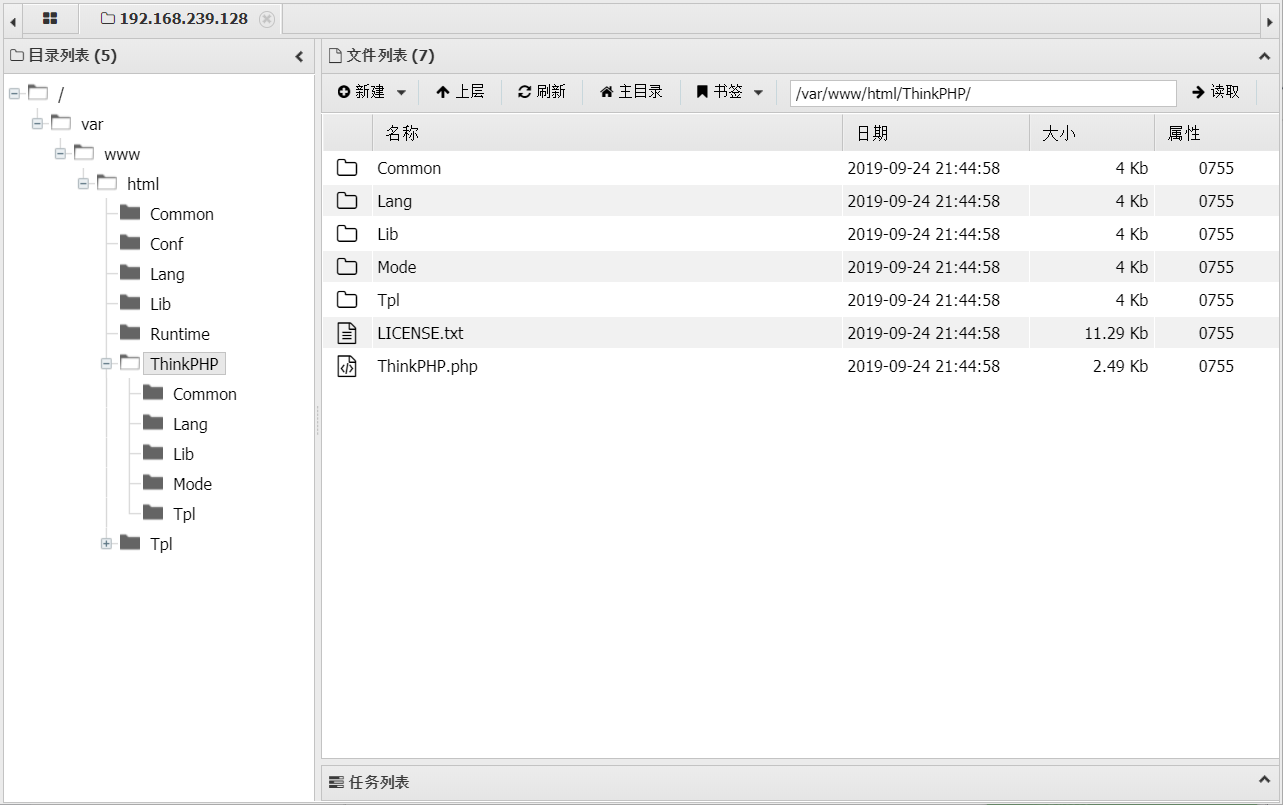
【vulhub漏洞复现】Thinkphp 2.x 任意代码执行
一、漏洞详情影响版本 thinkphp 2.x但是由于thinkphp 3.0版本在Lite模式下没有修复该漏洞,所以也存在该漏洞漏洞原因:e 和 /e模式匹配路由:e 配合函数preg_replace()使用, 可以把匹配来的字符串当作正则表达式执行; /e 可执行模式,…...

LeetCode 1145. 二叉树着色游戏 -- 简单搜索
二叉树着色游戏 提示 中等 199 相关企业 有两位极客玩家参与了一场「二叉树着色」的游戏。游戏中,给出二叉树的根节点 root,树上总共有 n 个节点,且 n 为奇数,其中每个节点上的值从 1 到 n 各不相同。 最开始时: 「一…...

HyperGBM的三种Early Stopping方式
本文作者:杨健,九章云极 DataCanvas 主任架构师 很多机器学习框架如都提供了Early Stopping策略,主要用来防止模型过拟合。和模型训练提前停止的目标不同,AutoML的Early Stopping策略更多考虑的是算力消耗和模型质量的平衡。 通…...
心系区域发展,高德用一体化出行服务平台“聚”力区域未来
交通,是城市的血脉。通过对人、资源、产业的连接,交通建设往往是城市和区域经济发展的前提。不过,在度过了“要想富,先修路”的初级建设阶段后,交通产业内部也出现了挑战,诸如城市秩序、发展成本、用户使用…...
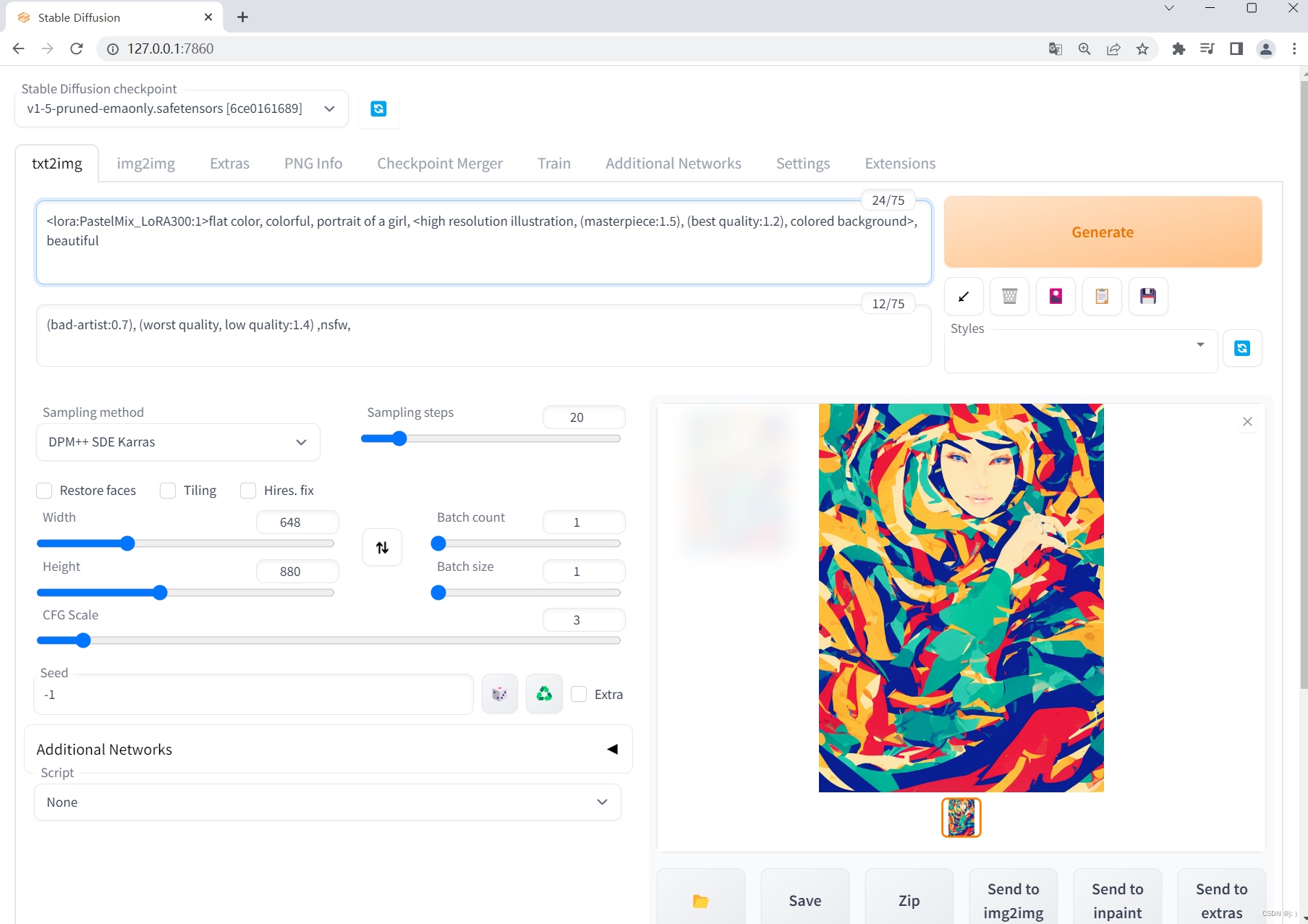
AI画图_stable-diffusion-webui安装使用指南(1)
本文章适用于: 有一定学习能力和钻研能力,遇到问题能合理使用搜索引擎尝试解决问题的人想在windows系统中尝试使用AI作画工具stable-diffusion-webui进行绘画的人有一定的计算机基础(会魔法上网、知道 python和Git)和英文阅读能力的人显卡为…...
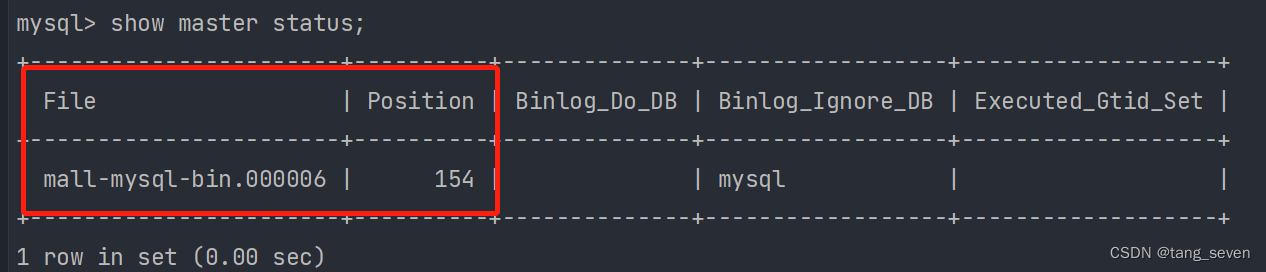
浅谈MySQL主从复制
目录 1.MySQL主从复制是什么 2.MySQL主从复制的意义 3.MySQL主从复制原理 4.数据同步一致性问题 5.实现方式 1.MySQL主从复制是什么 MySQL主从复制就是指数据可以从一台MySQL的主节点复制到一个或多个从节点。 MySQL默认采用异步复制方式,这样从节点不用一直访…...
docker-compose安装kafka和php简单测试
docker-compose.yml内容: version: 3.1 services: zookeeper: container_name: zookeeper image: zookeeper:3.6 ports: - 2181:2181 kafka: image: wurstmeister/kafka container_name: kafka depends_on: - zookeeper …...

【蓝桥云课】快速幂
问题描述:快速求aba^bab 方法一:常规方法相乘a∗a∗a∗a∗...∗aa*a*a*a*...*aa∗a∗a∗a∗...∗a 方法二:分治方法求aba^bab ab{1,b0a,b1ab2⋅ab2,b为偶数ab−12⋅ab12,b为奇数a^b\begin{cases} 1& \text{,b0}\\ a& \text{,b1}\\ a…...
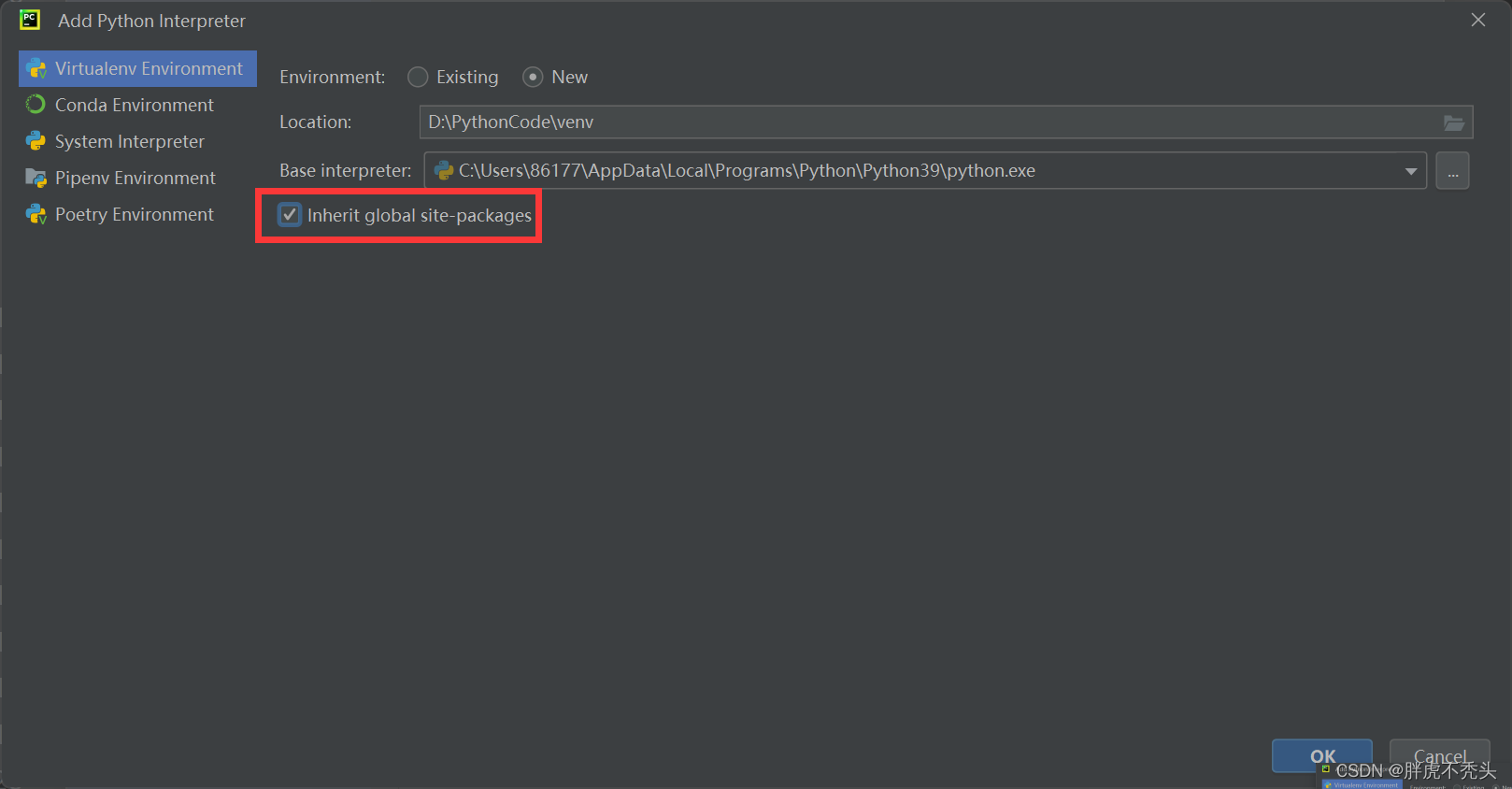
解决windows安装wxPython安装失败、速度过慢及PyCharm上wx包爆红问题
网上关于wxPython安装失败,安装速度过慢,以及安装成功后PyCharm中import wx仍然爆红的文章有很多,也特别杂,解决起来特别困难,今天在这里对问题的处理进行一个整合,希望能帮助到大家。 安装wxPython这里运用…...

封装小程序request请求[接口函数]
在这篇小程序API的Promise化文章中讲到小程序官方提供的异步API都是基于回调函数来实现的,在大量的使用这种回调函数就会造成回调地狱的问题,以及代码的可读性和可维护性差,通过对小程序API的Promise化能解决,那么本篇是来讲进行对…...

嵌入式 STM32 通讯协议--MODBUS
目录 一、自定义通信协议 1、协议介绍 2、网络协议 3、自定义的通信协议 二、MODBUS通信协议 1、概述 2、MODBUS帧结构 协议描述 3、MODBUS数据模型 4、MODBUS事务处理的定义 5、MODBUS功能码 6、功能码定义 7、MODBUS数据链路层 8、MODBUS地址规则 9、MO…...

互联网人看一看,这些神器你用过哪些?
很多小伙伴在剪辑视频的过程中经常可以看到一些语音素材,经常刷视频的小伙伴也可以看到很多视频中经常出现一些AI合成的声音或者音效,这些配音可以给视频增添很多亮点!那么大家都是怎么将文字转语音的呢?今天给大家分享5款非常专业…...
Kotlin学习:5.2、异步数据流 Flow
Flow一、Flow1、Flow是什么东西?2、实现功能3、特点4、冷流和热流5、流的连续性6、流的构建器7、流的上下文8、指定流所在协程9、流的取消9.1、超时取消9.2、主动取消9.3、密集型任务的取消10、背压和优化10.1、buffer 操作符10.2、 flowOn10.3、conflate 操作符10.…...
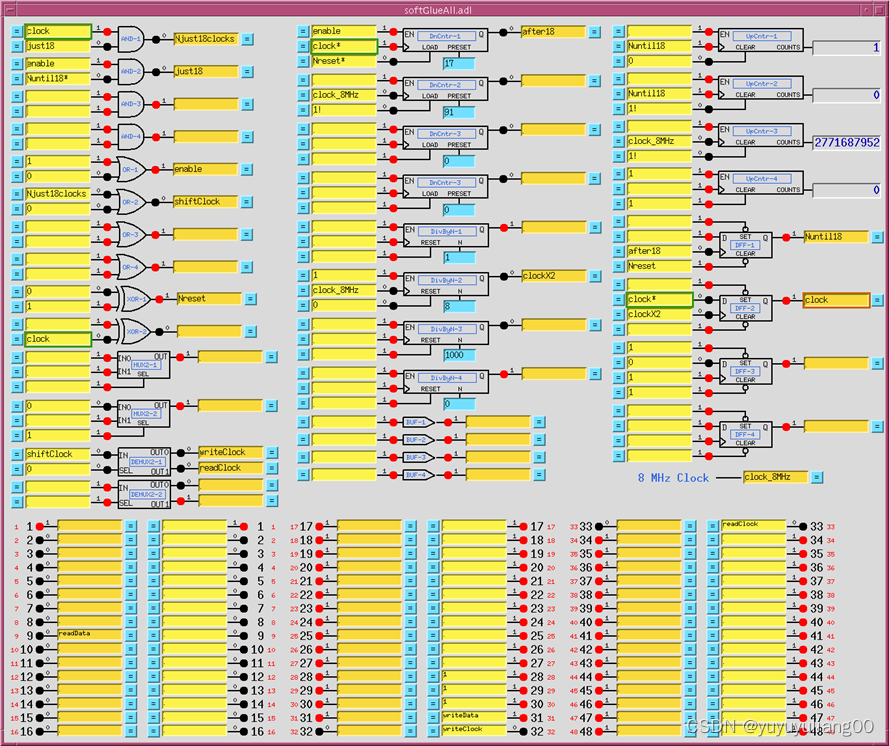
EPICS synApps介绍
一、synApps是什么? 1) 一个用于同步束线用户的EPICS模块集合。 2) EPICS模块 alive, autosave, busy, calc, camac, caputRecorder, dac128V, delaygen, dxp, ip, ip330, ipUnidig, love, mca, measComp, modbus, motor, optics, quadEM,…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
