凸优化专题1
多变量函数的求导与求梯度/矩阵求导
1. 导数
定义: 设f:Rn→Rm,且x∈intdomf,则f在点x的导数(或称Jacobian)记为矩阵Df(x)∈Rm×nf:\R^n \rightarrow \R^m, 且x\in \mathbf{int}\ \mathbf{dom} f, 则f 在点x的导\\数(或称Jacobian)记为矩阵 Df(x) \in \R^{m\times n}f:Rn→Rm,且x∈int domf,则f在点x的导数(或称Jacobian)记为矩阵Df(x)∈Rm×n, 定义如下
Df(x)ij=∂fi(x)∂xj,i=1,...,m,j=1,...,n(1)Df(x)_{ij} = \frac{\partial f_i(x)}{\partial x_j},\ i = 1,...,m,\ \ j = 1,...,n \tag{1} Df(x)ij=∂xj∂fi(x), i=1,...,m, j=1,...,n(1)
Df(x)ij表示矩阵Df(x)的第i行第j列元素Df(x)_{ij}表示矩阵Df(x)的第i行第j列元素Df(x)ij表示矩阵Df(x)的第i行第j列元素
2. 梯度
定义: 如果fff是一个实值函数(即f:Rn→Rf:\R^n \rightarrow \Rf:Rn→R), 易知其在点xxx导数Df(x)Df(x)Df(x)是一个行向量, 定义Df(x)Df(x)Df(x)的转置为其在点xxx处的梯度, 即
∇f(x)=Df(x)T(2)\nabla f(x) = Df(x)^T \tag{2} ∇f(x)=Df(x)T(2)
易知梯度为一个列向量.
注1: 梯度是针对实值函数的, 且其定义是基于Jacobian的, 也就是说现有导数才有梯度. 梯度的定义可以拓展到f:Sn→Rf:S^n \rightarrow \Rf:Sn→R, SnS^nSn指n阶实对称矩阵, 此处不再赘述.
注2:对于一般的f:Rn→Rmf:\R^n \rightarrow \R^mf:Rn→Rm, fff在点xxx附近的一阶近似记作:
f(x)+Df(x)(z−x),z∈δϵ(x)(3)f(x) + Df(x)(z-x), z \in \delta_\epsilon(x) \tag{3} f(x)+Df(x)(z−x),z∈δϵ(x)(3)
这和单变量函数的情形是一致的.
与之相对应, 对于一般的实值函数f:Rn→Rf:\R^n \rightarrow \Rf:Rn→R, 用梯度表示其一阶近似, 则有:
f(x)+∇f(x)T(z−x),z∈δϵ(x)(4)f(x) +\nabla f(x)^T(z-x), z \in \delta_\epsilon(x) \tag{4} f(x)+∇f(x)T(z−x),z∈δϵ(x)(4)
3. 链式法则
考虑f:Rn→Rm,且f在x处可微,x∈intdomf,并有g:Rn→Rp在f(x)处可微,f(x)∈intdomg,定义符合复合函数h:Rn→Rp,其中h(z)=g(f(z)),则有h在点x处可微,且其在点x处的导数为f:\R^n \rightarrow \R^m, 且f在x处可微, x\in \mathbf{int}\ \mathbf{dom}\ f, 并有g:\R^n \rightarrow \R^p\\在f(x)处可微, f(x)\in \mathbf{int}\ \mathbf{dom}\ g, 定义符合复合函数h:\R^n \rightarrow \R^p,其\\中h(z) = g(f(z)), 则有h在点x处可微, 且其在点x处的导数为f:Rn→Rm,且f在x处可微,x∈int dom f,并有g:Rn→Rp在f(x)处可微,f(x)∈int dom g,定义符合复合函数h:Rn→Rp,其中h(z)=g(f(z)),则有h在点x处可微,且其在点x处的导数为:
Dh(x)=Dg(f(x))Df(x)(5)Dh(x) = Dg(f(x))Df(x) \tag{5} Dh(x)=Dg(f(x))Df(x)(5)
特别地, 若f:Rn→R,g:R→R,则可以考虑h的梯度,只要取转置即可,根据定义有f:\R^n \rightarrow \R, g:\R \rightarrow \R, 则可以考虑h的梯度, 只要取转置\\即可, 根据定义有f:Rn→R,g:R→R,则可以考虑h的梯度,只要取转置即可,根据定义有:
∇h(x)=g′(f(x))∇f(x)(6)\nabla h(x) = g'(f(x))\nabla f(x) \tag{6} ∇h(x)=g′(f(x))∇f(x)(6)
这是很显然的结果, 只需要略加思索即可知道这是正确答案.
例题: 考虑f:Rn→R,domf=Rnf:\R^n \rightarrow \R, \mathbf{dom}\ f = \R^nf:Rn→R,dom f=Rn, 且
f(x)=ln∑i=1mexp(aiTx+bi)f(x) = \ln\sum_{i=1}^m \exp(a_i^T x+b_i) f(x)=lni=1∑mexp(aiTx+bi)
其中ai∈Rn,bi∈Ra_i \in \R^n, b_i \in \Rai∈Rn,bi∈R
请求出f(x)f(x)f(x)的梯度.
解:
设z(x)=∑i=1mexp(aiTx+bi)z(x) = \sum_{i=1}^m \exp(a_i^T x+b_i)z(x)=∑i=1mexp(aiTx+bi), 则根据链式法则, 有
Df(x)=Dlnz(x)=1zDz(x)Df(x) = D\ln z(x) = \frac{1}{z}Dz(x) Df(x)=Dlnz(x)=z1Dz(x)
设y(x):Rn→Rm,yi=exp(aiTx+bi)y(x) : \R^n \rightarrow \R^m, y_i = \exp(a_i^T x+b_i)y(x):Rn→Rm,yi=exp(aiTx+bi), 则有z=1Ty,其中1∈Rm,且每个元素均为1z = \mathbf{1}^T y, 其中\mathbf{1} \in \R^m, 且\\每个元素均为1z=1Ty,其中1∈Rm,且每个元素均为1
所以
y=exp(ATx+b)\begin{split} y = \exp(A^Tx+b) \end{split} y=exp(ATx+b)
其中
AT=[a1Ta2T⋮amT]A^T = \begin{bmatrix} a_{1}^T \\ a_{2}^T \\ \vdots \\ a_{m}^T \\ \end{bmatrix} AT=a1Ta2T⋮amT
所以
Df(x)=1zDz(x)=1z1TDy(x)\begin{split} Df(x) &= \frac{1}{z}Dz(x) \\ &= \frac{1}{z} \mathbf{1}^T Dy(x) \\ \end{split} Df(x)=z1Dz(x)=z11TDy(x)
其中Dy(x)Dy(x)Dy(x)为
Dy(x)=[∂y1x1∂y1x2⋯∂y1xn∂y2x1∂y2x2⋯∂y2xn⋮⋮⋱⋮∂ymx1∂ymx2⋯∂ymxn]∈Rm×nDy(x) = \begin{bmatrix} \frac{\partial y_1}{x_1} & \frac{\partial y_1}{x_2} & \cdots & \frac{\partial y_1}{x_n} \\ \frac{\partial y_2}{x_1} & \frac{\partial y_2}{x_2} & \cdots & \frac{\partial y_2}{x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_m}{x_1} & \frac{\partial y_m}{x_2} & \cdots & \frac{\partial y_m}{x_n} \end{bmatrix} \in\R^{m \times n} Dy(x)=x1∂y1x1∂y2⋮x1∂ymx2∂y1x2∂y2⋮x2∂ym⋯⋯⋱⋯xn∂y1xn∂y2⋮xn∂ym∈Rm×n
易知
Dy(x)ij=∂yixj=exp(aiTx+bi)⋅aijDy(x)_{ij} = \frac{\partial y_i}{x_j} = \exp(a_i^T x+b_i) \cdot a_{ij} Dy(x)ij=xj∂yi=exp(aiTx+bi)⋅aij
其中aij为aiT的第j个元素a_{ij}为a_{i}^T的第j个元素aij为aiT的第j个元素
Dy(x)Dy(x)Dy(x)也可写作
Dy(x)=diag{y1,y2,⋯,ym}⋅[a1Ta2T⋮amT]Dy(x) = diag\{ y_{1}, y_{2}, \cdots, y_{m} \} \cdot \begin{bmatrix} a_{1}^T \\ a_{2}^T \\ \vdots \\ a_{m}^T \\ \end{bmatrix} Dy(x)=diag{y1,y2,⋯,ym}⋅a1Ta2T⋮amT
所以
Df(x)=1z1T⋅diag{y1,y2,⋯,ym}⋅[a1Ta2T⋮amT]=1z1T⋅diag{y1,y2,⋯,ym}⋅AT\begin{split} Df(x) &= \frac{1}{z} \mathbf{1}^T \cdot diag\{ y_{1}, y_{2}, \cdots, y_{m} \} \cdot \begin{bmatrix} a_{1}^T \\ a_{2}^T \\ \vdots \\ a_{m}^T \\ \end{bmatrix} \\ &= \frac{1}{z} \mathbf{1}^T \cdot diag\{ y_{1}, y_{2}, \cdots, y_{m} \} \cdot A^T \end{split} Df(x)=z11T⋅diag{y1,y2,⋯,ym}⋅a1Ta2T⋮amT=z11T⋅diag{y1,y2,⋯,ym}⋅AT
所以
∇f(x)=1zA⋅diag{y1,y2,⋯,ym}⋅1=1zA⋅[exp(a1Tx+b1)exp(a2Tx+b2)⋮exp(amTx+bm)]其中z=∑i=1mexp(aiTx+bi)\begin{split} \nabla f(x) &= \frac{1}{z} A \cdot diag\{ y_{1}, y_{2}, \cdots, y_{m} \} \cdot \mathbf{1} \\ &=\frac{1}{z} A \cdot \begin{bmatrix} \exp(a_1^T x + b_1) \\ \exp(a_2^T x + b_2) \\ \vdots \\ \exp(a_m^T x + b_m) \\ \end{bmatrix} \\ 其中z &= \sum_{i=1}^m \exp(a_i^T x+b_i) \end{split} ∇f(x)其中z=z1A⋅diag{y1,y2,⋯,ym}⋅1=z1A⋅exp(a1Tx+b1)exp(a2Tx+b2)⋮exp(amTx+bm)=i=1∑mexp(aiTx+bi)
4. 二阶导数
对于实值函数f:Rn→R,且x∈intdomf,则f在点x的二阶导数(或称Hessian]matrix)记为矩阵∇2f(x)∈Rn×n,其中f:\R^n \rightarrow \R, 且x\in \mathbf{int}\ \mathbf{dom} f, 则f 在点x的二阶导\\数(或称Hessian] matrix)记为矩阵 \nabla^2 f(x) \in \R^{n\times n}, 其中f:Rn→R,且x∈int domf,则f在点x的二阶导数(或称Hessian]matrix)记为矩阵∇2f(x)∈Rn×n,其中
∇2f(x)ij=∂2f(x)∂xi∂xj,i,j=1,...,n(7)\nabla^2 f(x)_{ij} = \frac{\partial^2 f(x)}{\partial x_i \partial x_j}, \ i,j = 1,...,n \tag{7} ∇2f(x)ij=∂xi∂xj∂2f(x), i,j=1,...,n(7)
易知对于一般的实值函数f:Rn→Rf:\R^n \rightarrow \Rf:Rn→R, 用hessian matrix表示其二阶近似, 则有:
f^(z)=f(x)+∇f(x)T(z−x)+12(z−x)T∇2f(x)(z−x)z∈δϵ(x)\hat{f}(z) = f(x) +\nabla f(x)^T(z-x) + \frac{1}{2}(z-x)^T\nabla^2 f(x)(z-x)\\ z \in \delta_\epsilon(x) f^(z)=f(x)+∇f(x)T(z−x)+21(z−x)T∇2f(x)(z−x)z∈δϵ(x)
易知下列关系式成立
D∇f(x)=∇2f(x)(8)D\nabla f(x) = \nabla ^2f(x) \tag{8} D∇f(x)=∇2f(x)(8)
相关文章:

凸优化专题1
多变量函数的求导与求梯度/矩阵求导 1. 导数 定义: 设f:Rn→Rm,且x∈intdomf,则f在点x的导数(或称Jacobian)记为矩阵Df(x)∈Rmnf:\R^n \rightarrow \R^m, 且x\in \mathbf{int}\ \mathbf{dom} f, 则f 在点x的导\\数(或称Jacobian)记为矩阵 Df(x) \in \R^{m\times n}f:Rn→Rm,且…...
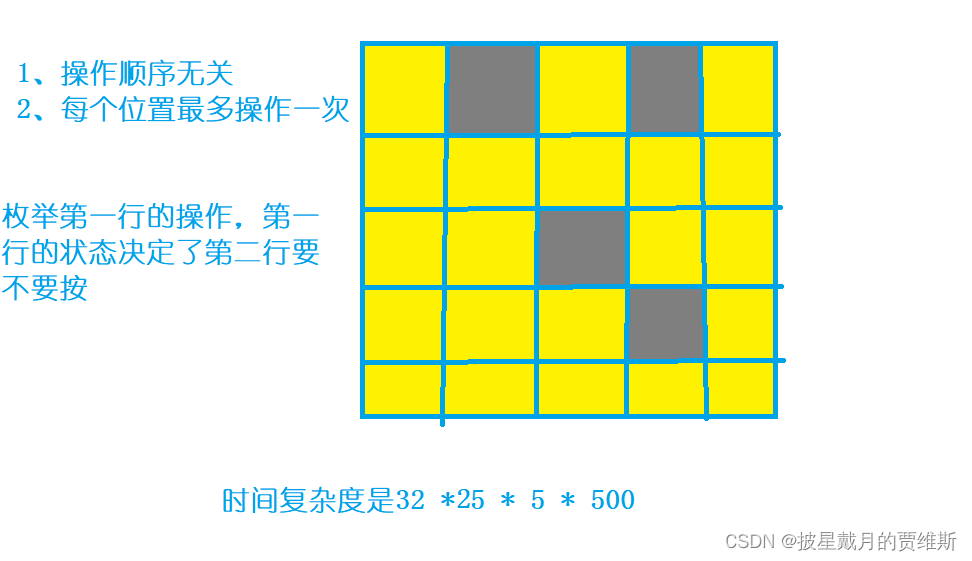
【蓝桥杯每日一题】递推算法
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙我与杀戮之中绽放,亦如黎明的花…...
Unity性能优化: 性能优化之内存篇
前言 本文和传统的内存优化不一样,不是讲如何降低内存占用,而是讲编程开发中要注意的内存问题以及一些内存技术的演变与原理。 对惹,这里有一个游戏开发交流小组,希望大家可以点击进来一起交流一下开发经验呀 1: Application进程…...

华为OD机试题,用 Java 解【内存资源分配】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...

微服务之Nacos注册与配置
🏠个人主页:阿杰的博客 💪个人简介:大家好,我是阿杰,一个正在努力让自己变得更好的男人👨 目前状况🎉:24届毕业生,奋斗在找实习的路上🌟 …...
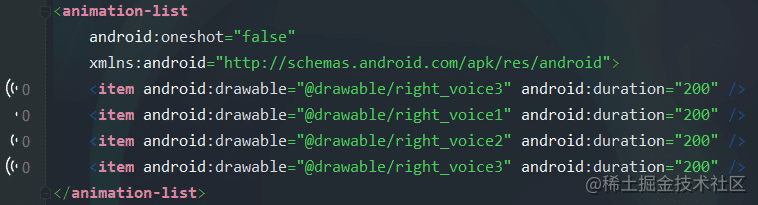
Android 动画详解
Android动画的分类与使用学习Android必不可少的就是动画的使用了,在Android版本迭代的过程中,出现了很多动画框架,这里做一个总结。Android动画类型分类逐帧动画【Frame Animation】,即顺序播放事先准备的图片。补间动画【Tween A…...

Linux -- 程序 进程 线程 概念引入
程序与进程 :程序 :什么是程序 ???伪官方 : 二进制文件,文件存储在磁盘中,例如 /usr/bin 目录下 。 是静态。 简单讲 :# 我们都学习了语言,比如下面这串代…...
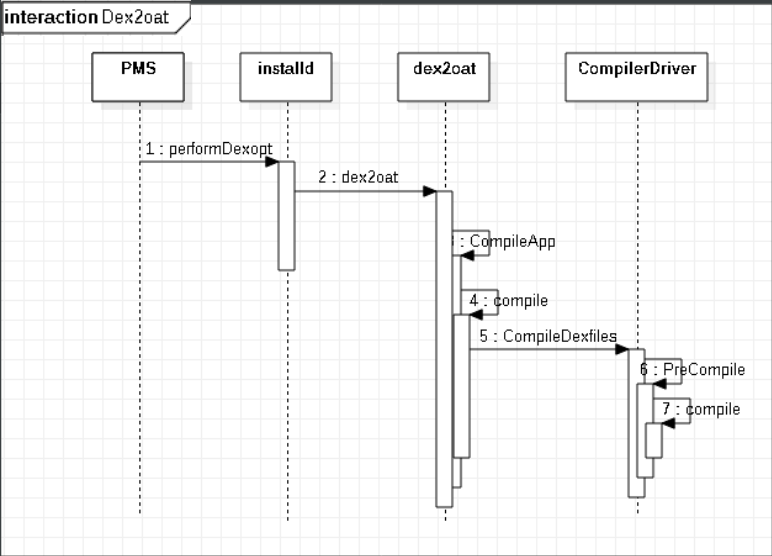
Android ART dex2oat
一、什么是dex2oat Dex2oat (dalvik excutable file to optimized art file) ,是一个对 dex 文件进行编译优化的程序,在我们的 Android 手机中的位置是 /system/bin/dex2oat,对应的源码路径为 android/art/dex2oat/dex2oat.cc,通…...
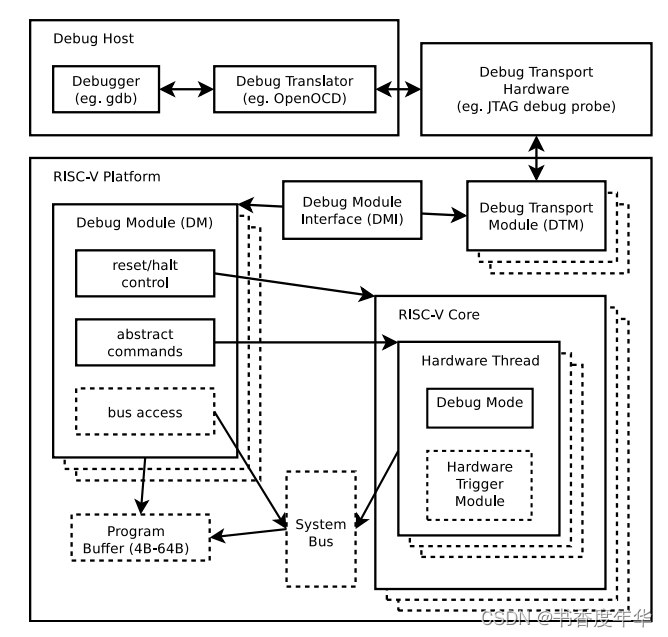
「RISC-V Arch」RISC-V 规范结构
日期:20230228 规范分类 根据 RISC-V 设计哲学,其规范文档也是高度模块化的: ISA 规范(2 篇) 非特权规范特权规范 非 ISA 规范(6篇) Trace规范ABI 规范外部调试规范PLIC 规范SBI 规范UEFI 协…...

【C】线程控制
创建线程 #include <pthread.h>int pthread_create(pthread_t * thread,const pthread_attr_t * attr,void *(*start_routine)(void*), void * arg);返回值:成功返回0,失败返回错误号。 thread:成功返回后,新创建的线程的…...
Maven工程打jar包的N种方式
Maven工程打jar包 一、IDEA自带打包插件二、maven插件打包2.1 制作瘦包(直接打包,不打包依赖包)2.2 制作瘦包和依赖包(相互分离)2.3 制作胖包(项目依赖包和项目打为一个包)2.4 制作胖包…...

一文了解GPU并行计算CUDA
了解GPU并行计算CUDA一、CUDA和GPU简介二、GPU工作原理与结构2.1、基础GPU架构2.2、GPU编程模型2.3、软件和硬件的对应关系三、GPU应用领域四、GPUCPU异构计算五、MPI与CUDA的区别一、CUDA和GPU简介 CUDA(Compute Unified Device Architecture)…...
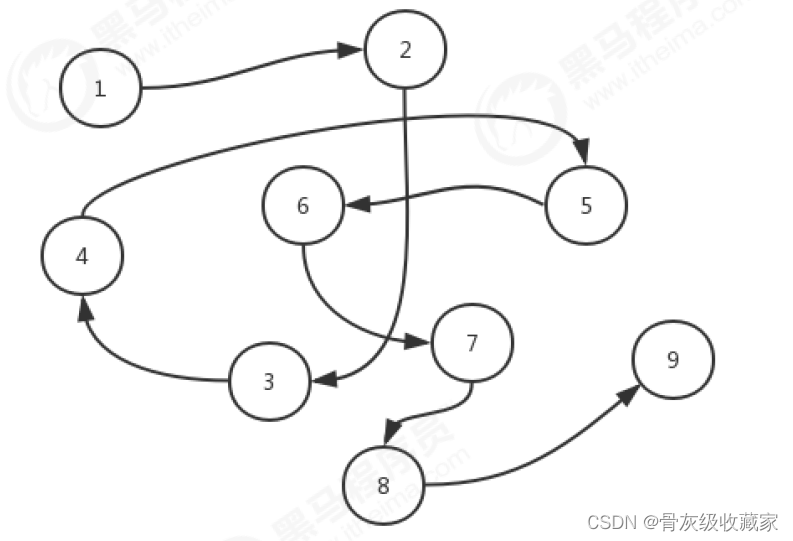
全网资料最全Java数据结构与算法(1)
一、数据结构和算法概述 1.1什么是数据结构? 官方解释: 数据结构是一门研究非数值计算的程序设计问题中的操作对象,以及他们之间的关系和操作等相关问题的学科。 大白话: 数据结构就是把数据元素按照一定的关系组织起来的集合&a…...

【项目实战】SpringMVC拦截器HandlerInterceptor入门介绍
一、拦截器介绍 拦截器是应用程序级框架中常用的拦截用户请求、实施业务流程控制的模式,它可以将一些公共的、重复发生的业务逻辑从业务处理代码中独立出来,使系统的结构更加清晰,程序的复杂度也减小了。 拦截器是一个常见的特性,它可以实现任何自定义功能,而无需调整业…...

阿里淘宝新势力造型合伙人P8、年薪百万的欧阳娜娜也躲不过的魔鬼面试,看的我心服口服
阿里淘宝新势力造型合伙人P8、年薪百万的欧阳娜娜跳槽了,这不是关键。 她参加了网易有道明星语音录音员/代言人的面试,这也不是关键。 关键是她教科书式的面试过程,狠狠地给我们上了一课。 我是无意间刷到的这个视频的时候,就一…...

深度学习笔记:不同的反向传播迭代方法
1 随机梯度下降法SGD 随机梯度下降法每次迭代取梯度下降最大的方向更新。这一方法实现简单,但是在很多函数中,梯度下降的方向不一定指向函数最低点,这使得梯度下降呈现“之”字形,其效率较低 class SGD:"""随机…...
ElasticSearch 学习笔记总结(三)
文章目录一、ES 相关名词 专业介绍二、ES 系统架构三、ES 创建分片副本 和 elasticsearch-head插件四、ES 故障转移五、ES 应对故障六、ES 路由计算 和 分片控制七、ES集群 数据写流程八、ES集群 数据读流程九、ES集群 更新流程 和 批量操作十、ES 相关重要 概念 和 名词十一、…...

深入理解border以及应用
深入border属性以及应用👏👏 border这个属性在开发过程中很常用,常常用它来作为边界的。但是大家真的了解border吗?以及它的形状是什么样子的。 我们先来看这样一段代码:👏 <!--* Author: syk 185901…...

如何复现论文?什么是论文复现?
参考资料: 学习篇—顶会Paper复现方法 - 知乎 如何读论文?复现代码?_复现代码是什么意思 - CSDN 我是如何复现我人生的第一篇论文的 - 知乎 在我看来,论文复现应该有一个大前提和分为两个层次。 大前提是你要清楚地懂得自己要…...
 A~C)
22.2.28打卡 Codeforces Round #851 (Div. 2) A~C
A题 One and Two 题面翻译 题目描述 给你一个数列 a1,a2,…,ana_1, a_2, \ldots, a_na1,a2,…,an . 数列中的每一个数的值要么是 111 要么是 222 . 找到一个最小的正整数 kkk,使之满足: 1≤k≤n−11 \leq k \leq n-11≤k≤n−1 , anda1⋅a2⋅……...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
