进制转换(二进制,八进制,十进制,十六进制)涵盖整数与小数部分,内容的图片全为手写【详细图解】

各种进制之间的相互转换
- 1. 各进制表示数
- 1.1 数码
- 1.2 基数
- 1.3 位权
- 2. 十进制转换为其他进制
- 2.1 整数部分
- 2.2 小数部分
- 3. 其他进制转换为十进制
- 4. 二进制转换为八进制
- 5. 二进制转换为十六进制
- 6. 八进制转换为十六进制
1. 各进制表示数
二进制:0,1逢二进一
八进制:0 ~ 7逢八进一
十进制:0 ~ 9逢十进一
十六进制:0 ~ 9,A ~ F逢十六进一
进制转换由一组数码符号和两个基本因素“基数”与“位权”构成。
基数是指:进位计数制中所采用的数码(数制中用来表示“量”的符号)的个数。
位权是指:进位制中每一固定位置对应的单位值。
1.1 数码
每个进制中能够使用的数字符号,就称为该进制的数码。
如:二进制的数码就是 1,0.
1.2 基数
该进制中能够使用数码的个数就成为该进制的基数。
如:八进制基数就是8.
1.3 位权
该进制基数的n次方,n表示……2,1,0,-1,-2……个位
如:十六进制,16的n次方。
2. 十进制转换为其他进制
2.1 整数部分
整数部分:就是十进制的数码除以要转制的基数,取其余数,由下到上写结果。
十进制转换二进制 如:(43)10 = ()2

十进制转换为八进制 如:(43)10 = ()8

十进制转换十六进制 如:(87)10 = ()16

2.2 小数部分
用小数部分乘要转制的基数,取其整数,从上到下取结果。
如:(0.625)10 = ()2

3. 其他进制转换为十进制
就是利用其它进制每位的数码乘该位该进制的位权,所有数之和就是对应的十进制数。
如:(326)8 = ()10
3 * 8 ^2 + 2 * 8^1+ 1* 8 ^ 0
如:(C916)16 = (12*16^ 3 + 9 * 16^ 2 + 1 * 16 ^ 1+9 *16 ^0)10
4. 二进制转换为八进制
把二进制从右向左(整数部分),每三位代表一位八进制数,不够三位,前面补0。
如:
(1110101011)2 = ()8
(742)8 = ()2

5. 二进制转换为十六进制
把二进制从右向左(整数部分),每四位代表一位十六进制,不够四位,前面补0。
如:
(1110101011)2 = ()16
(DF9)16 = ()2

6. 八进制转换为十六进制
如:(563)8 = ()16

如果这份博客对大家有帮助,希望各位给恒川一个免费的点赞作为鼓励,并评论收藏一下,谢谢大家!!!
制作不易,如果大家有什么疑问或给恒川的意见,欢迎评论区留言。
相关文章:

进制转换(二进制,八进制,十进制,十六进制)涵盖整数与小数部分,内容的图片全为手写【详细图解】
各种进制之间的相互转换1. 各进制表示数1.1 数码1.2 基数1.3 位权2. 十进制转换为其他进制2.1 整数部分2.2 小数部分3. 其他进制转换为十进制4. 二进制转换为八进制5. 二进制转换为十六进制6. 八进制转换为十六进制1. 各进制表示数 二进制:0,1逢二进一 八…...
谈谈XR关键技术及VR/AR/MR/XR关系
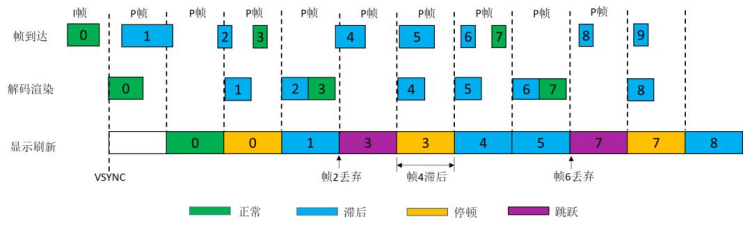
一、先别被VR/AR/MR/XR搞晕,说说区别虚拟现实(Virtual Reality,VR)、增强现实(Augmented Reality,AR)等业务以其三维化、自然交互、空间计算等完全不同于当前移动互联网的特性,被认为…...
acwing1562 微博转发(宽搜)
微博被称为中文版的 Twitter。 微博上的用户既可能有很多关注者,也可能关注很多其他用户。 因此,形成了一种基于这些关注关系的社交网络。 当用户在微博上发布帖子时,他/她的所有关注者都可以查看并转发他/她的帖子,然后这些人…...

如何使用Arsenal快速部署功能强大的Bug Bounty工具
关于Arsenal Arsenal是一个功能强大且使用简单的Shell脚本(Bash),该工具专为漏洞赏金猎人设计,在该工具的帮助下,我们可以轻松在自己环境中安装并部署目前社区中功能最为强大的网络侦查工具、漏洞扫描工具和其他安全研…...
python网络爬虫(理论+实战)——正则表达式再讨论、常用正则表达式整理)
(十)python网络爬虫(理论+实战)——正则表达式再讨论、常用正则表达式整理
系列文章目录 (1)python网络爬虫—快速入门(理论+实战)(一) (2)python网络爬虫—快速入门(理论+实战)(二) (3) python网络爬虫—快速入门(理论+实战)(三) (4)python网络爬虫—快速入门(理论+实战)(四) (5)...

MyBatis-Plus特性及插件整合
了解MyBatis-Plus 什么是MyBatis-Plus? mybatisPlus在mybatis的基础上继续针对CRUD操作进行优化,在原有的基础上提供了公共的接口BaseMapper,我们在创建接口Mapper时只需要继承这个接口即可调用MyBatisPlus已经提供好的方法,sql…...
应用篇|网络安全知识培训考试,答题小程序操作指引
网络安全知识培训考试,答题小程序操作指引关于全民防诈反诈宣传或者网络安全知识学习,如何进行组织一场微信线上答题考试?可以在小程序“护网专题信息安全知识竞答”,先创建一个学习单位/小组,再邀请成员加入单位/小组…...

官方不推荐@Autowired
1用lombok注解 2 构造器...

【牛客刷题专栏】0x0E:JZ6 从尾到头打印链表(C语言编程题)
前言 个人推荐在牛客网刷题(点击可以跳转),它登陆后会保存刷题记录进度,重新登录时写过的题目代码不会丢失。个人刷题练习系列专栏:个人CSDN牛客刷题专栏。 题目来自:牛客/题库 / 在线编程 / 剑指offer: 目录前言问题…...

Zeppelin安装
1、下载Zeppelin 下载地址:Download 2.解压 [rootguo147 install]# tar -zxvf zeppelin-0.10.0-bin-all.tgz -C ../soft/ //修改文件名 [rootguo147 soft]# mv zeppelin-0.10.0-bin-all/ zeppelin 3.配置 //进入conf 目录 [rootguo147 conf]# pwd /opt/soft/zepp…...

【蓝桥杯选拔赛真题38】python目标值判断 青少年组蓝桥杯python 选拔赛STEMA比赛真题解析
目录 python目标值判断 一、题目要求 1、编程实现 2、输入输出 二、解题思路...

Python jieba分词如何添加自定义词和去除不需要长尾词
Python jieba分词如何添加自定义词和去除不需要长尾词 作者:虚坏叔叔 博客:https://xuhss.com 早餐店不会开到晚上,想吃的人早就来了!😄 通过如下代码,读取一个txt的高频词汇: # 找到高频词汇t…...
云打包苹果证书生成、上架和应用截屏攻略
在使用apicloud或hbuilderx这些跨端的开发工具开发移动应用的时候,假如是打包ios应用,是需要生成苹果证书、证书profile文件,和对应用上架的。首先要普及一个概念,苹果的应用是无法像安卓那样挂在自己的服务器上下载直接安装就可以…...
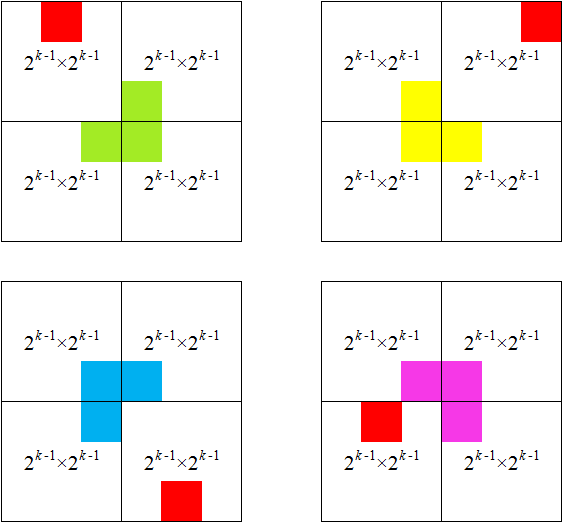
洛谷 U91193:棋盘覆盖问题 ← 分治法
【题目来源】https://www.luogu.com.cn/problem/U91193【问题描述】 在一个2^k * 2^k(k≥0)个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格。现在用4种不同形状的 L型(占3小格)骨牌覆…...

基于OMAPL138+FPGA核心板多核软件开发组件MCSDK开发入门(下)
本文测试板卡为创龙科技 SOM-TL138F 是一款基于 TI OMAP-L138(定点/浮点 DSP C674x + ARM9)+ 紫光同创 Logos/Xilinx Spartan-6 低功耗 FPGA 处理器设计的工业级核心板。核心板内部OMAP-L138 与 Logos/Spartan-6 通过 uPP、EMIFA、I2C 通信总线连接,并通过工业级 B2B连接器引…...

熵,线性规划,半监督自监督聚类打标签
1.熵 信息熵是消除不确定性所需信息量的度量。 信息熵就是信息的不确定程度,信息熵越小,信息越确定。 对象的信息熵是正比于它的概率的负对数的,也就是 I©−log(pc) 其中n为事件的所有可能性。 为什么使用交叉熵?在机器学习…...
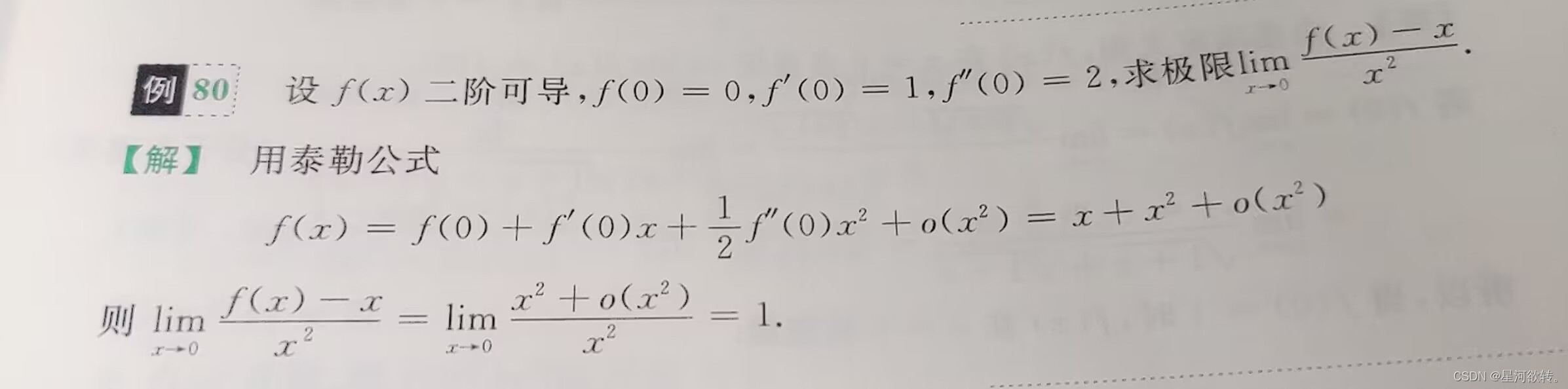
求极限方法总结
1.利用四则运算法则求极限 2.利用两个重要极限求极限 //0除以0型 //1的无穷次方型 3.利用等价无穷小替换替换求极限 //在等价替换时注意和差项 4.利用洛必达法则求极限 5.利用夹逼准则求极限 6.利用单调有界数列极限准则求极限 7.利用无穷小的性质求极限 8.利用函数的连续性…...

Flutter Scrollable 中ViewPort滚动原理
关于Flutter Sliver组件内容可以参考下面这位博主博客,写的已经非常好了,这里就不再赘述。 38、Flutter之 可滚动组件简介_flutter 可滑动_风雨「83」的博客-CSDN博客 通过阅读上面的博客,我们已经知道了Scrollable和Viewport基础概念&#…...

多目标粒子群结合极限学习机ELM求解帕累托前沿,MOPSO-ELM
目录 背影 parte前沿的定义 注意事项 基于多目标粒子群结合极限学习机的帕累托前沿求解帕累托前沿 主要参数 MATLAB代码 效果图 结果分析 展望 背影 在目标优化过程种,很多时候都两个或者多个目标,并且目标函数不能同时达到最优,鱼与熊掌不可兼得,这个时候可以通过求解帕…...
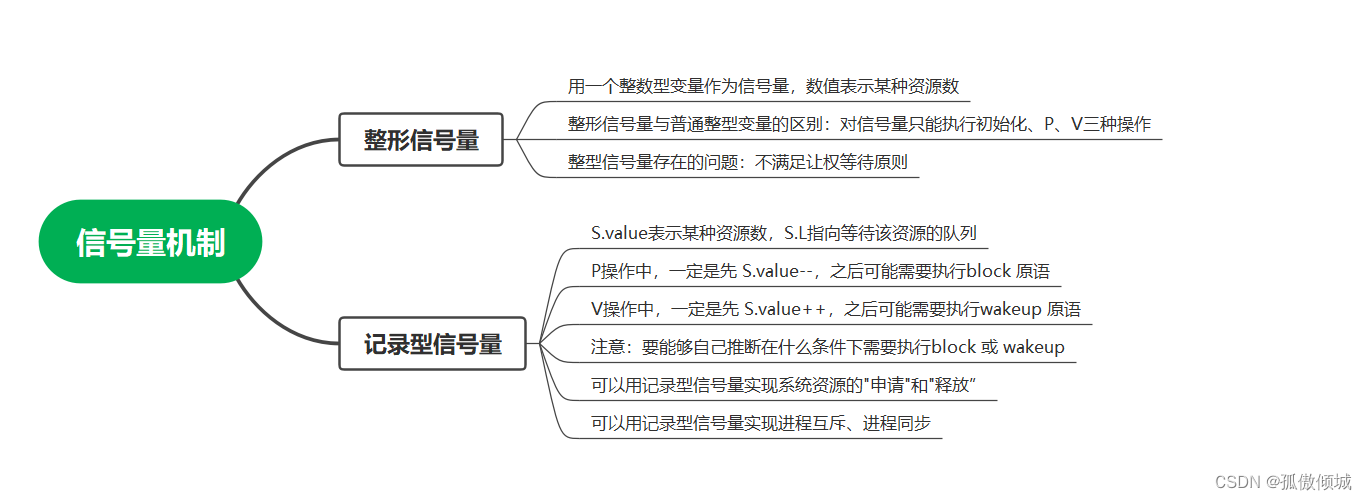
(二十)操作系统-信号量机制
文章目录一、知识预览二、前篇文章知识点回顾三、信号量机制四、信号量机制—整形信号量五、信号量机制—记录型信号量六、总结一、知识预览 二、前篇文章知识点回顾 进程互斥的四种软件实现方式:单标志法、双标志先检查、双标志后检查、Peterson算法。(…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
