数据结构入门--时间 空间复杂度
数据结构入门 时间 空间复杂度解析
目录
一. 算法效率
二. 时间复杂度
2.1 时间复杂度的概念
2.2 大O的渐进表示法
2.3 题目练习
题目一
题目二
题目三
题目四
题目五
题目六
题目七
三. 空间复杂度
3.1 题目练习
题目一
题目二
题目三
一. 算法效率
算法效率分析分为两种:第一种是时间效率,第二种是空间效率。
时间效率被称为时间复杂度,而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主要衡量一个算法所需要的额外空间,在计算机发展的早期,计算机的存储容量很小,所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。我们如今已经不需要再特别关注一个算法的空间复杂度。
总结经过这么久技术的发展 我们对于时间复杂度的要求高于空间复杂度的要求
二. 时间复杂度
2.1 时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
2.2 大O的渐进表示法
我们直接上题目
// 请计算一下Func1基本操作执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i) {for (int j = 0; j < N ; ++ j){++count;}for (int k = 0; k < 2 * N ; ++ k) {++count;}int M = 10;while (M--) {++count; }}printf("%d\n", count);
}
我们经过计算可以发现 这个函数需要运算的次数是 n的平方 加上 2*n 再加上10
当我们的n等于10的时候 它的次数是130
放我们的n是100的时候 它的次数是10210
当我们的n是1000的时候 它的次数是1002010
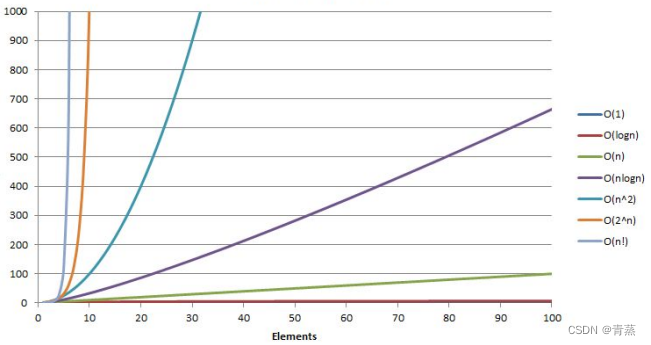
我们可以发现 它执行的次数实际上只跟n的平方有强相关性
这个时候我们只需要了解到这个程序的最高次项 我们就能估算出这个程序所需要运行的数量级
那么这里就能够引生出我们的大O的渐进表示法
推导大O阶方法:
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
当n等于10的时候 它运行的次数就是100
当n等于100的时候 它运行的次数就是10000
当n等于1000的时候 它运行的次数就是1000000
此外 如果说随着我们输入的不同空间复杂度也有所改变的话 那么我们取最坏的空间复杂度作为我们的复杂度
2.3 题目练习
题目一
void Func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; ++ k) {++count; }
int M = 10;
while (M--) {++count; }
printf("%d\n", count);
}
它计算的此时是2N+10
实际上的复杂度就是O(N)
题目二
void Func3(int N, int M) {
int count = 0;
for (int k = 0; k < M; ++ k) {++count; }
for (int k = 0; k < N ; ++ k) {++count; }
printf("%d\n", count);
}
它的计算的次数是 M+N次
实际的空间复杂度就是O(max(M,N))
题目三
void Func4(int N) {
int count = 0;
for (int k = 0; k < 100; ++ k) {++count; }
printf("%d\n", count);
}这里实际上和N没有关系 它会计算100次
所以说它的次数是一个常数
常数的时间复杂度是O(1)
题目四
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n) {
assert(a);
for (size_t end = n; end > 0; --end) {int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break; }
}
这里实际运行的次数是end的平方-n之后除以2
所以说 它的时间复杂度是O(N^2)
题目五
int BinarySearch(int* a, int n, int x) {
assert(a);
int begin = 0;
int end = n-1;
while (begin < end) {int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid;elsereturn mid; }
return -1; }
它最好的运算情况是一次
运算最坏的情况是logN
所以说它的时间复杂度是logN
题目六
long long Factorial(size_t N)
{return N < 2 ? N : Factorial(N-1)*N;
}实际上它的它的空间复杂度是O(N)
题目七
long long Fibonacci(size_t N)
{return N < 2 ? N : Fibonacci(N-1)+Fibonacci(N-2);
}实际上它的复杂度是 2的0次方加上2的一次放+…+2的N-1次方减去N
实际上它的它的空间复杂度是O(2^N)
实例答案及分析:
- 实例1基本操作执行了2N+10次,通过推导大O阶方法知道,时间复杂度为 O(N)
- 实例2基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)
- 实例3基本操作执行了10次,通过推导大O阶方法,时间复杂度为 O(1)
- 实例4基本操作执行最好1次,最坏N次,时间复杂度一般看最坏,时间复杂度为 O(N)
- 实例5基本操作执行最好N次,最坏执行了(N*(N+1)/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为 O(N^2)
- 实例6基本操作执行最好1次,最坏O(logN)次,时间复杂度为 O(logN) ps:logN在算法分析中表示是底数为2,对数为N。有些地方会写成lgN。
- 实例7通过计算分析发现基本操作递归了N次,时间复杂度为O(N)。
- 实例8通过计算分析发现基本操作递归了2N次,时间复杂度为O(2N)。
三. 空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
3.1 题目练习
题目一
void BubbleSort(int* a, int n) {assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
实际上冒泡排序并没有占用额外的空间
所以说它使用的空间是常量级别的
所以说它的空间复杂度是O(1)
题目二
long long* Fibonacci(size_t n) {if(n==0)return NULL;long long * fibArray =(long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i ] = fibArray[ i - 1] + fibArray [i - 2];}return fibArray ;
}
这里用来计算fib数 开辟了n+1个空间
实际上的空间复杂度是O(N)
题目三
long long Factorial(size_t N) {return N < 2 ? N : Factorial(N-1)*N; }它实际上开辟了N到1数量的空间
所以说它的空间复杂度是O(N)
实际上这里我们要明确一点
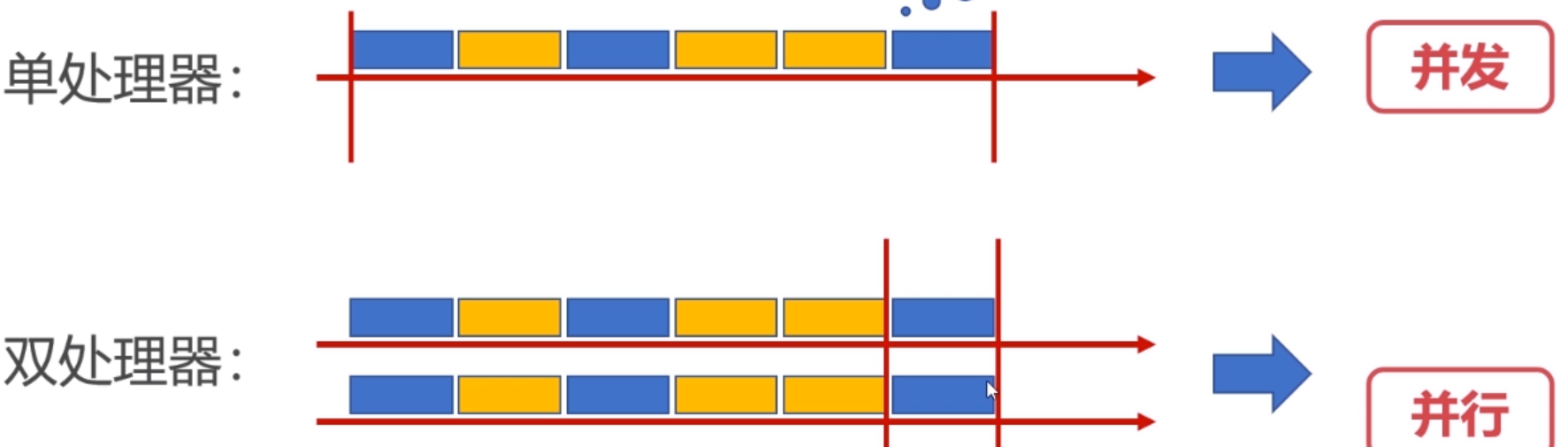
时间是不能复用的
空间是可以复用的
相关文章:

数据结构入门--时间 空间复杂度
数据结构入门 时间 空间复杂度解析 目录 一. 算法效率 二. 时间复杂度 2.1 时间复杂度的概念 2.2 大O的渐进表示法 2.3 题目练习 题目一 题目二 题目三 题目四 题目五 题目六 题目七 三. 空间复杂度 3.1 题目练习 题目一 题目二 题目三 一. 算法效率 算法效率…...
计算机操作系统第一章
操作系统引论1.1操作系统的目标和作用定义:操作系统是控制管理计算机系统的硬软件,分配调度资源的系统软件。目标:方便性,有效性(提高系统资源的利用率、提高系统的吞吐量),可扩充性,…...

ARM LDREX/STREX指令以及独占监控器详解
一、目的Linux驱动开发中有一个特别重要的知识点必须掌握,即并发、竞态以及同步。什么是并发?多个执行单元(进程、线程、中断)同时对一个共享资源的进行访问;此处的共享资源可以是外设、内存或者软件层面的全局变量静态…...

吉林大学 程序设计基础 2022级 实验复盘 2.23
本人能力有限,发出只为帮助有需要的人。 以下为实验课的复盘,内容会有大量失真,请多多包涵。 此次实验限时一个小时,时间很紧张,很多内容可能并不准确。 1.输出有规律的字母串 输入输出如下; 输入&…...

Linux系列 常用命令(目录和文件管理)vi和vim 编辑使用,(笔记)
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.常用命令(目录和文件管理) 1.查看文件内容 2.统计…...
OpenCV入门(一)Python环境的搭建
OpenCV入门(一)Python环境的搭建 因为有点Python基础,并且Python是比较好入门的编程语言,所以,机器视觉后面打算在Python这个平台下进行。 Windows平台OpenCV的Python开发环境搭建 1、Python 的下载与安装 Python是…...
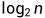
3.查找算法:顺序查找和二分查找
查找查找,是指在一些数据元素中,通过一定的方法找出与给定关键字相同的数据元素的过程。列表查找(线性表查找):从列表中查找指定元素输入:列表,待查找元素输出:元素下标(…...
攻不下dfs不参加比赛(七)
标题 为什么练dfs题目总结重点为什么练dfs 相信学过数据结构的朋友都知道dfs(深度优先搜索)是里面相当重要的一种搜索算法,可能直接说大家感受不到有条件的大家可以去看看一些算法比赛。这些比赛中每一届或多或少都会牵扯到dfs,可能提到dfs大家都知道但是我们为了避免眼高手…...

精确光度预测计算工具:AGi32 Crack
什么是AGi32? AGi32首先是一种用于精确光度预测的计算工具:一种技术工具,可以计算任何情况下的照度,协助灯具放置和瞄准,并验证是否符合任意数量的照明标准。 然而,要增强对光度学结果的理解,还…...
47个SQL性能优化技巧,看到就是赚到
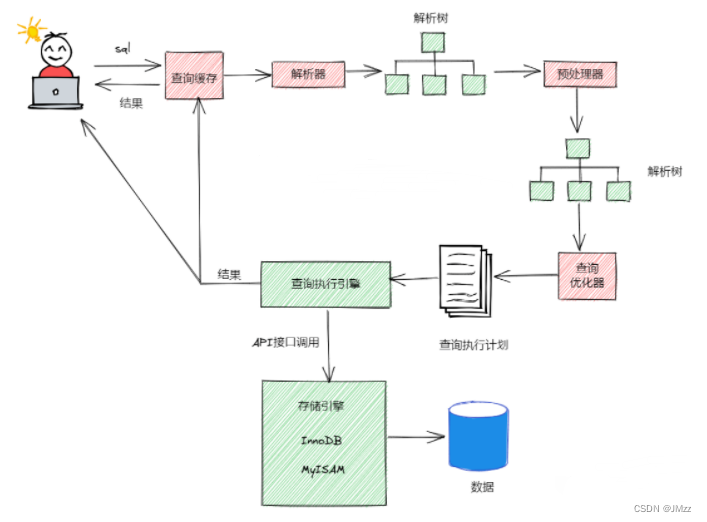
1、先了解MySQL的执行过程 了解了MySQL的执行过程,我们才知道如何进行sql优化。 (1)客户端发送一条查询语句到服务器; (2)服务器先查询缓存,如果命中缓存,则立即返回存储在缓存中的…...
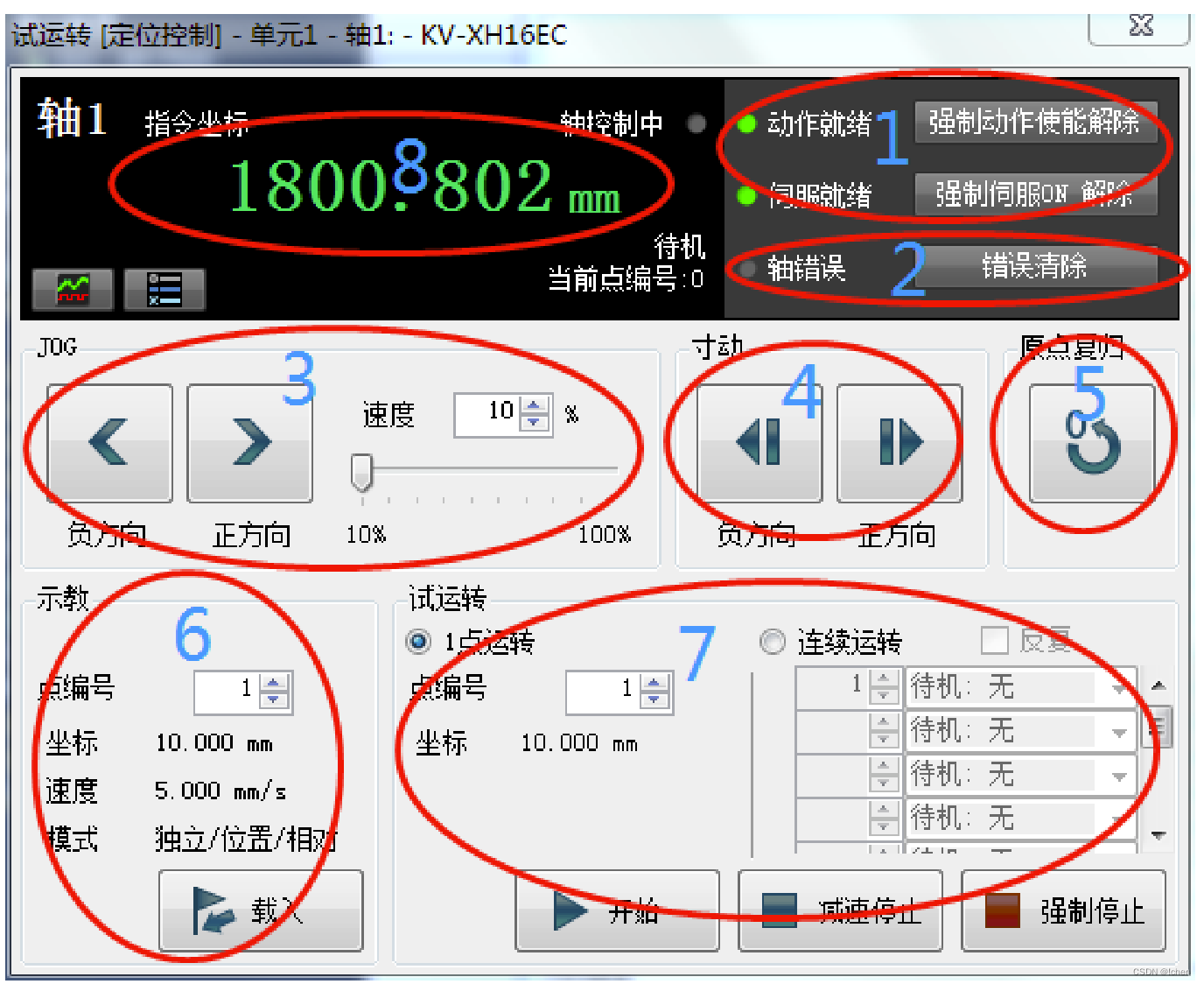
汇川SV660N与基恩士 KV7500 控制器调试说明
1. 伺服相关部分配置 1.1 伺服相关版本 SV660N 试机建议使用“SV660N-Ecat_v0.09.xml”及以上设备描述文件。 SV660N 单板软件版本建议为“H0100901.4”及更高版本号。 1.2 相关参数说明 SV660N 对象字典中 60FD 的含义较 IS620N 有所更改:bit0、1、2 分别为负限位…...

图观 | ChatGTP是如何通过知识图谱回答问题的?
文/Emma Z1950年,图灵发表了具有里程碑意义的论文《计算机器与智能》(Computing Machinery and Intelligence),提出了一个关于机器人的著名判断原则——图灵测试,也被称为图灵判断,它指出如果第三者无法辨别…...
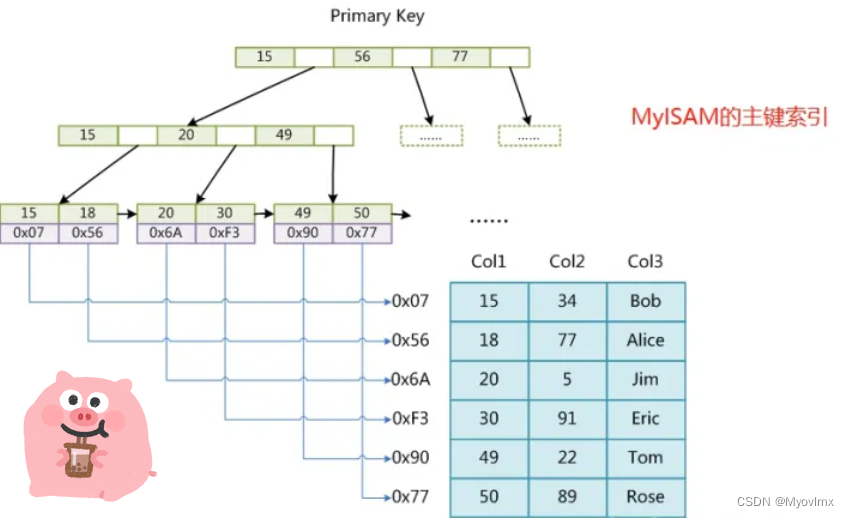
Mysql的索引
为什么写这篇文章呢~最近在梳理公司的数据库,在查看表结构的时候发现了这个 CREATE TABLE esp_5_N (ID int(11) NOT NULL AUTO_INCREMENT,pId int(11) DEFAULT NULL,EsFileId varchar(32) DEFAULT NULL,obligate1 varchar(45) DEFAULT NULL,obligate2 varchar(45) …...

计算机的发展
个人简介:云计算网络运维专业人员,了解运维知识,掌握TCP/IP协议,每天分享网络运维知识与技能。个人爱好: 编程,打篮球,计算机知识个人名言:海不辞水,故能成其大;山不辞石…...

理解Spring中的依赖注入和控制反转
依赖注入(Dependency Injection)是一种面向对象编程的设计模式,用于解决对象之间的依赖关系。它的基本思想是将对象的创建和管理工作交给容器来完成,而不是在应用程序中手动创建和管理对象,从而达到松耦合、易维护、易…...
XXL-JOB
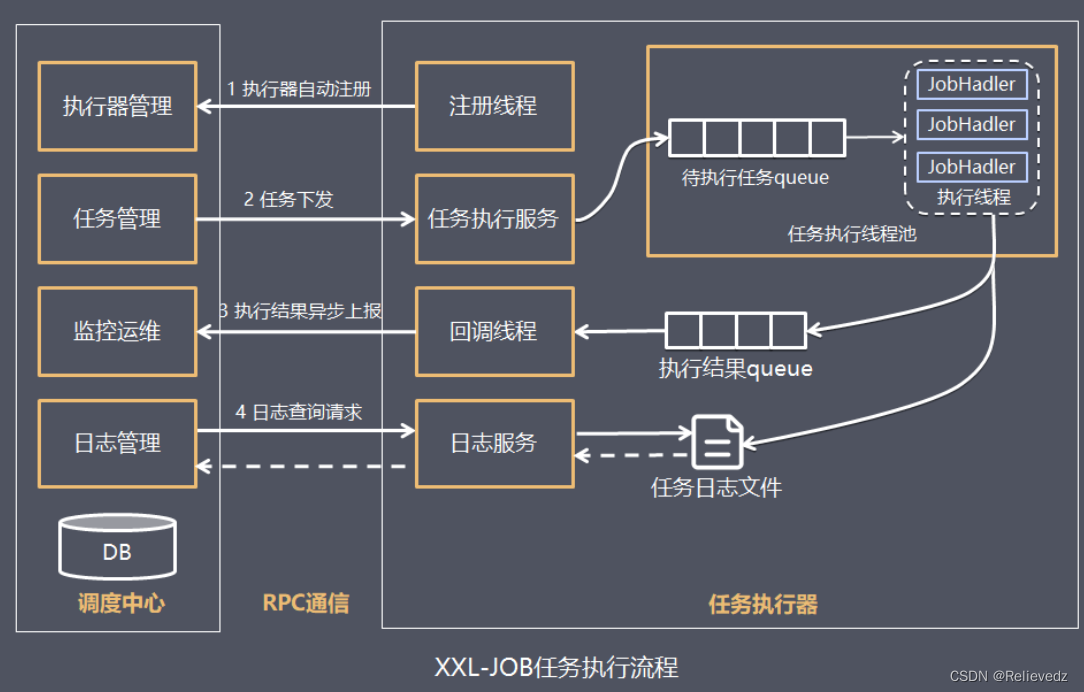
XXL-JOB介绍 XXL-JOB是一个轻量级分布式任务调度平台,其核心设计目标是开发迅速、学习简单、轻量级、易扩展。现已开放源代码并接入多家公司线上产品线,开箱即用。 官网:https://www.xuxueli.com/xxl-job/ 文档:分布式任务调度…...

「牛客网C」初学者入门训练BC134,BC136
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练 🔥座右铭:“不要等到什么都没有了,才下定决心去做” 🚀🚀🚀大家觉不错…...

华为OD机试题【翻转单词顺序】用 C++ 进行编码 (2023.Q1)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明翻转单…...
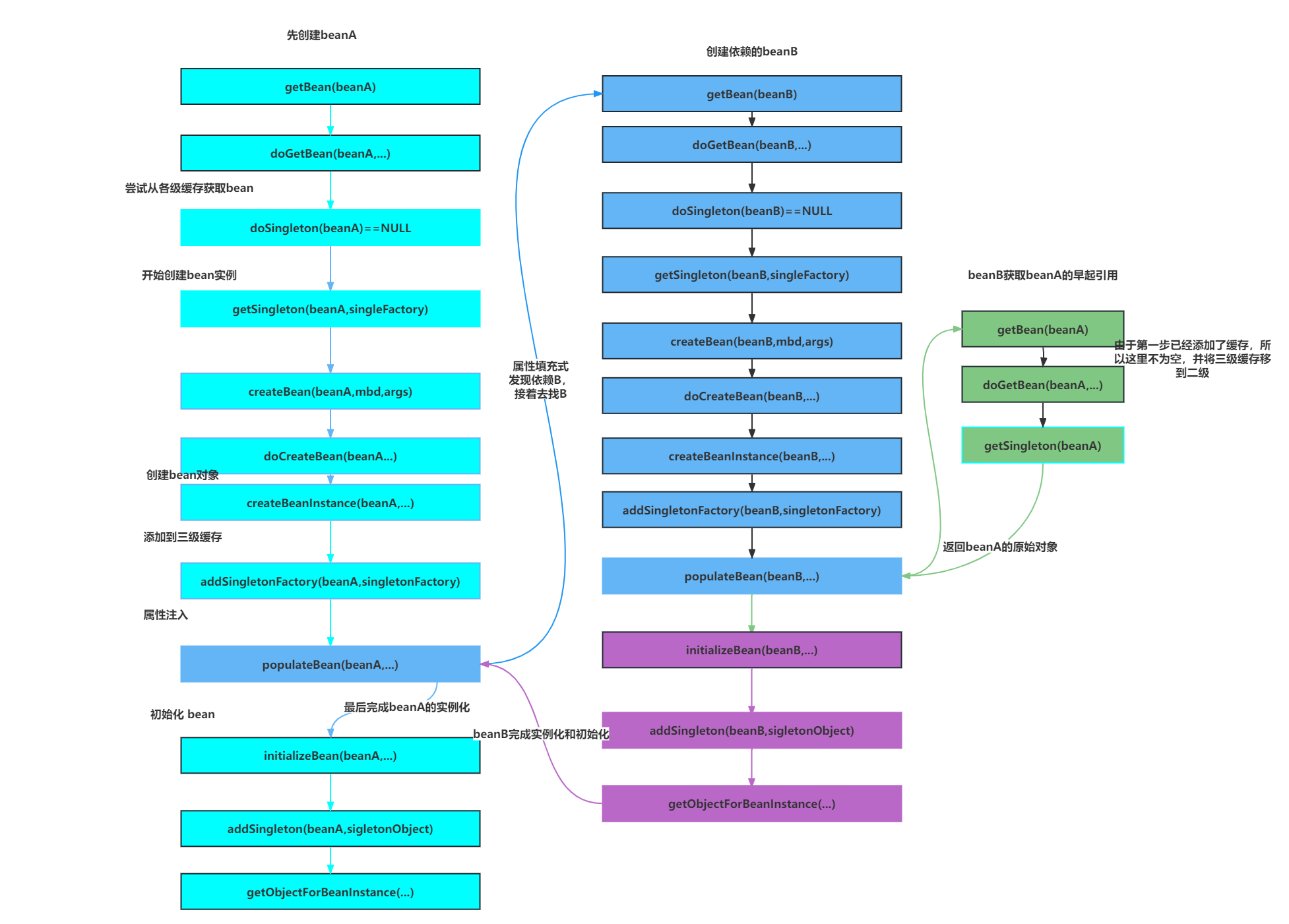
4.Spring【Java面试第三季】
4.Spring【Java面试第三季】前言推荐4.Spring27_Aop的题目说明要求Spring的AOP顺序AOP常用注解面试题28_spring4下的aop测试案例业务类新建一个切面类MyAspect并为切面类新增两个注解:spring4springboot1.5.9pom测试类29_spring4下的aop测试结果aop正常顺序异常顺序…...

ZLibrary使用说明-Zlirbrary
ZLibrary使用说明如果您是一位书虫,那么ZLibrary是一个值得一试的网站。该网站提供了大量的免费电子书籍,涵盖了各种不同的主题和类别。下面是一些有关如何使用ZLibrary的详细说明:第1步:访问ZLibrary网站要使用ZLibraryÿ…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
