线性代数学习-2
线性代数学习-2
- 矩阵消元
- 消元
- 回代
- 消元矩阵
- 置换矩阵
- 逆矩阵
本文转载于https://herosunly.blog.csdn.net/article/details/88713747
该文章本人认为十分有用,便自己敲一遍笔记加固印象
原文链接 原文
这个笔记感觉比我老师讲的更加透彻,清晰。很好的展示了线性代数的原理,强烈推荐看原文
上篇文章讲的是如何从定型的方式(列向量)分析出对于任意的b,是的Ax=b有解。这片文章则具体讲解如何求Ax=b方程组的解。简单总结如下,主要是讲定性问题转换成定量解决
矩阵消元
消元
高斯消元法是计算机软件求解线性方程组最常用的方法。高斯消元法就是通过对方程组中的某两个方程进行适当的数乘和加法(线性空间的两大基本运算),以达到将某一个未知数系数变为零,从而削减未知数的目的。其中每一步的目标是消除未知数(保证主元不为零的前提下)。
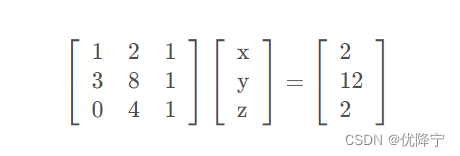
我们将矩阵左上角的1称之为**“主元一”(最好都是1),第一步要通过消元将第一列中除了住院之外的数字均变化为0.操作方法就是用之后的每一行减去第一行的适当倍数**,此例中第二行应减去第一行的3倍。之后应对第三行做类似操作,本例中三行第一列数字已经为0,故不用进行操作
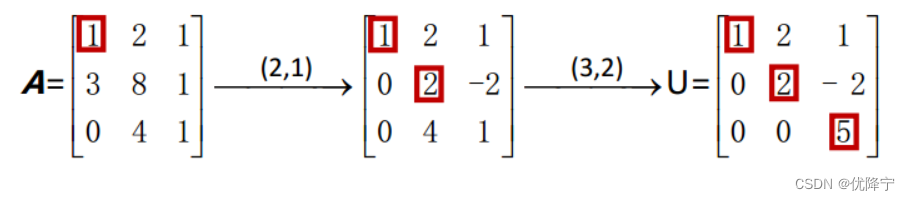
处在第二行第二列的主元为2,因此用第三行减去第二行的两倍进行消元,得到第三个主元为5.
矩阵A为可逆矩阵,消元结束后得到上三角阵U,即主对角线以下都是零的方阵成为上三角矩阵。
其左侧下半部分的元素均为0,而主元1、2、5分列在U的对角线上。主元之积即行列式的值(行列式只是方阵的一个性质)。
回代
做方程的高斯消元时,需要对等式右侧的b做同样的加法和数乘运算。手工计算时中比较有效率的方法是应用“增广矩阵”,将b插入矩阵的最后一列,然后进行相应的运算。
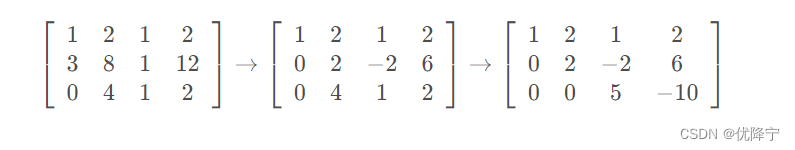
此时我们将原方程Ax=b转化成了新的方程Ux=从,其中c=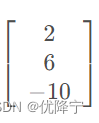
从最后一行得到z=-2,依次回代可以得到x=2和y=1。以上高斯消元的求解线性方程步骤。在线性代数中比较重要的就是将之前所说的“第二行减去第一行的3倍”这种操作条例变为矩阵化的数学语言。
消元矩阵
矩阵运算的核心内容就是对“行”或者“列”进行独立操作
如前文“列图像”,系数矩阵乘以未知数向量,相当于对系数矩阵的列向量进行线性组合。矩阵乘以列向量
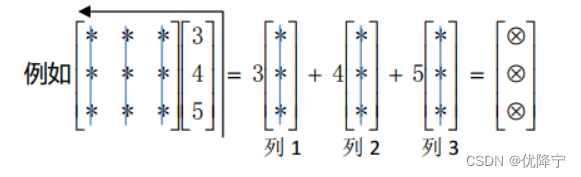
与之相对称,矩阵左乘行向量则是对矩阵的行向量进行线性组合。
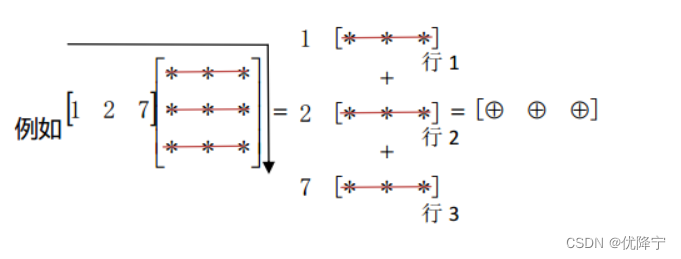
“列”操作就像是把向量开进矩阵,而“行操作”这个就像把向量倒车进入矩阵(如图中箭头所示)
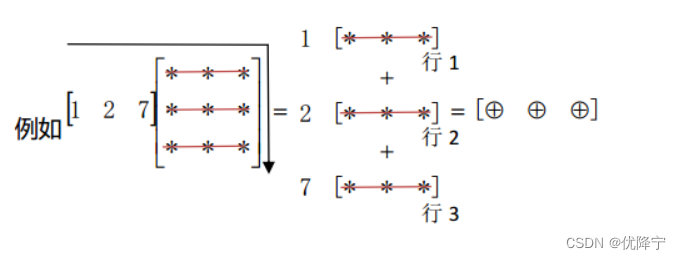



本质一样,但是这个计算介绍理解方法与教科书上相比简单很多
置换矩阵
置换矩阵的本质就是左乘或者右乘某个矩阵,从而完成行变换或者列变换
左乘置换矩阵可以完成原矩阵的行变换,右乘置换矩阵则为列变换
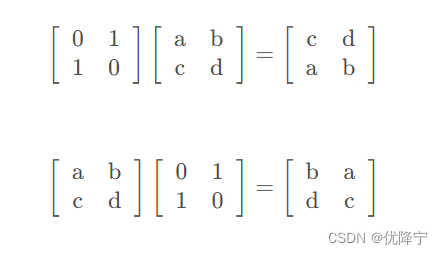
上述变换简称左行右列。左边是行变换比较容易理解的话,则转置之后就可以理解右边是列变换
逆矩阵
这里主要讨论消元矩阵的逆矩阵。消元矩阵之逆矩阵的实施效果就是抵消原矩阵的校园操作。消元矩阵实现了原矩阵A的操作,使第二行行向量[3,8,1]减掉了第一行的[1,2,1]的三倍变为[0,2,-2],则逆向操作就应该是把现在的第二行行向量[0,2,-2]加上第一行[1,2,1]的3倍,从而变回原来的第二行[3,8,1]。

相关文章:

线性代数学习-2
线性代数学习-2矩阵消元消元回代消元矩阵置换矩阵逆矩阵本文转载于https://herosunly.blog.csdn.net/article/details/88713747 该文章本人认为十分有用,便自己敲一遍笔记加固印象原文链接 原文这个笔记感觉比我老师讲的更加透彻,清晰。很好的展示了线性…...

Java 类
Java类是Java编程语言中的基本概念之一,用于描述对象的属性和方法。本文将详细介绍Java类的作用、定义和使用,以及在实际工作中的应用。 什么是Java类? Java类是一种用于描述对象的模板或蓝图。它定义了一个对象的属性和方法,以…...

GO中sync 包的 RWMutex 读写互斥锁
文章目录背景RWMutex 简介代码验证多个协程请求读锁 RLock() 和 RLock()读写交错 RLock() 和 Lock()写入的时候读取读取的时候写入请求多个写Lock() 和 Lock()背景 Mutex 互斥锁是严格锁定读和写,如果我们需要单独对读或者写添加锁需要使用 sync包的RWMutex 针对读…...
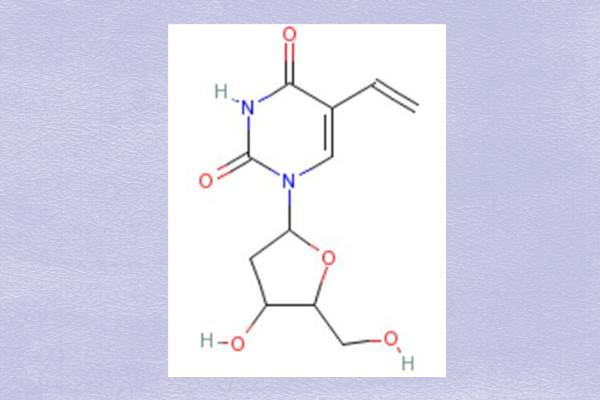
糖化学试剂55520-67-7,5-vinyl-2-deoxyuridine,5-乙烯基-2-脱氧尿苷特点分析说明
5-vinyl-2-deoxyuridine(5-VdU),5-vinyl-2-deoxyuridine,5-Vinyldeoxyuridine5-乙烯基-2-脱氧尿苷 | CAS:55520-67-7 | 纯度:95%试剂信息:CAS:55520-67-7所属类别:糖化学分子量:C11H…...

五年携手共话,FISCO BCOS为数实相生注入新动能
2月24日,作为深圳国际金融科技节系列活动之一,由深圳市地方金融监督管理局指导,微众银行、金链盟主办的“2022产业区块链年度峰会暨FISCO BCOS五周年生态大会”(下称“大会”)在深圳顺利召开。本次大会以“数实相生&am…...

特征可视化技术t-SNE
特征可视化技术t-SNE 一、理论介绍 想要了解t-SNE的数学原理可以参考t-SNE完整笔记 关于t-SNE的使用过程中有以下几点需要注意: t-SNE算法并不是每次都能产生相似结果。 t-SNE算法使得距离的概念适应于数据集中的区域密度变化。因此,它自然而然地扩大…...
.NET 导入导出Project(mpp)以及发布后遇到的Com组件问题
最近公司项目有一个对Project导入导出的操作,现在市面上能同时对Project进行导入导出的除了微软自带的Microsoft.Office.Interop.MSProject,还有就是Aspose.Tasks for .NET。但因为后者是收费软件且破解版的现阶段只到18.11,只支持.net Frame…...

centos 8安装配置 yum/dnf镜像源 以及 docker相关操作
Docker简介 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux或Windows操作系统的机器上,也可以实现虚拟化,容器是完全使用沙箱机制,相互之间不会有任何接口。 Docker组成部分: 镜…...

java基础之线程池
线程池1.线程池1.1 线程状态介绍1.2 线程池-基本原理1.3 线程池-Executors默认线程池1.4 线程池-Executors创建指定上限的线程池1.5 线程池-ThreadPoolExecutor1.6 线程池-参数详解1.7 线程池-非默认任务拒绝策略2. 原子性2.1 volatile-问题2.2 volatile解决2.3 synchronized解…...
Substrate 基础 -- 教程(Tutorials)
官网 github DOC 面向未来的区块链框架 Substrate 使开发人员能够快速、轻松地构建适合任何用例的未来 证明区块链(future proof blockchains)。 Substrate 文档包括区块链构建器(blockchain builders)和parachain 项目团队的概念、过程和参考信息。…...

一个线程两次调用start()方法会出现什么情况?
第17讲 | 一个线程两次调用start()方法会出现什么情况? 今天我们来深入聊聊线程,相信大家对于线程这个概念都不陌生,它是 Java 并发的基础元素,理解、操纵、诊断线程是 Java 工程师的必修课,但是你真的掌握线程了吗&am…...

看完再拿五分,软考高项时政提分必备
时事政治题作为软考信息系统项目管理师当中的必考题,每年都让不少考生头疼,主要吧,它一不在教材里,二考的又很随意,如果不是平时积累,专门注意去看,有时候很难答得对,弄得这几分就完…...
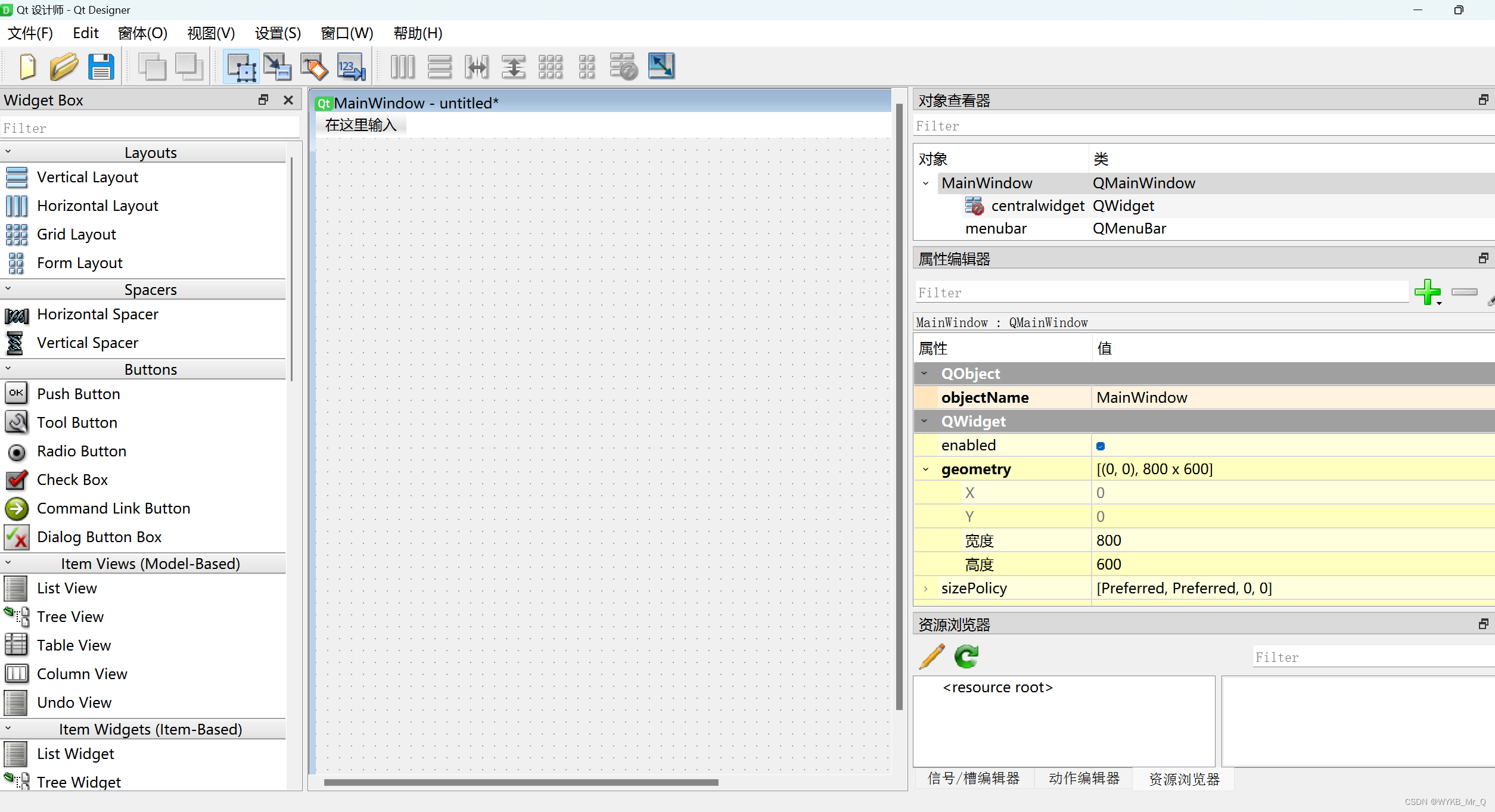
界面开发(1) --- PyQt5环境配置
PyQt5环境配置 第一步:首先安装社区版Pycharm 下载地址:https://www.jetbrains.com/pycharm/download/#sectionwindows 第二步:安装Anaconda3,配置虚拟环境 下载地址:https://www.anaconda.com/ 第三步࿱…...
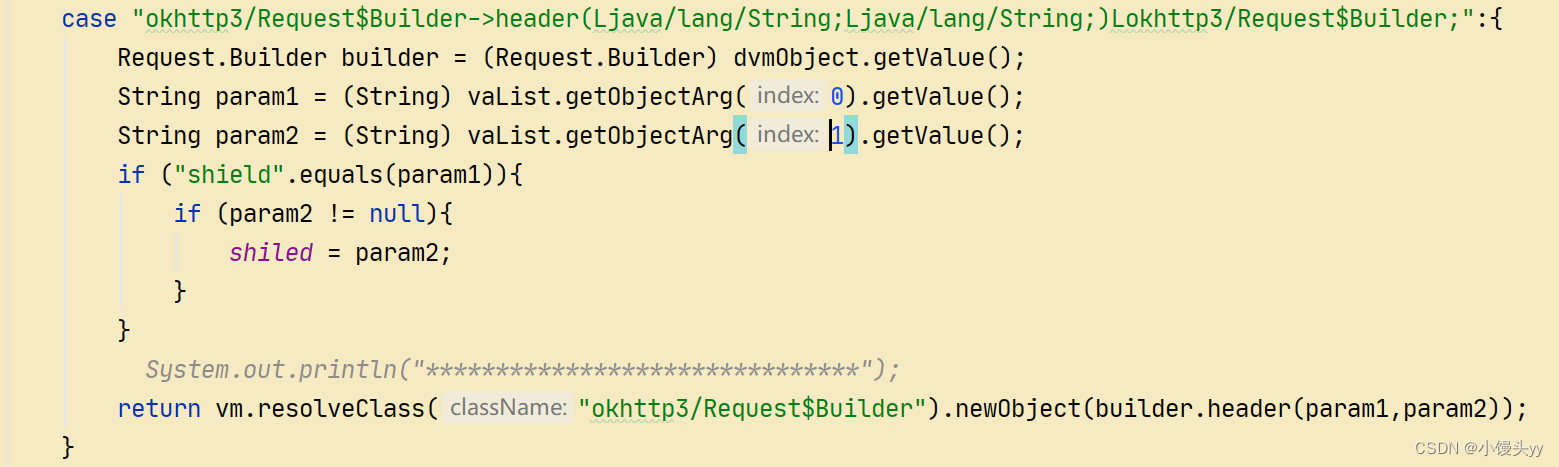
shield分析
本文仅供学习交流,只提供关键思路不会给出完整代码,严禁用于非法用途,若有侵权请联系我删除!技术交流合作请私信! 熟练打开Fiddler设置好手机代理,摆弄半天一直抓不到包,应该是小红书监测到了F…...
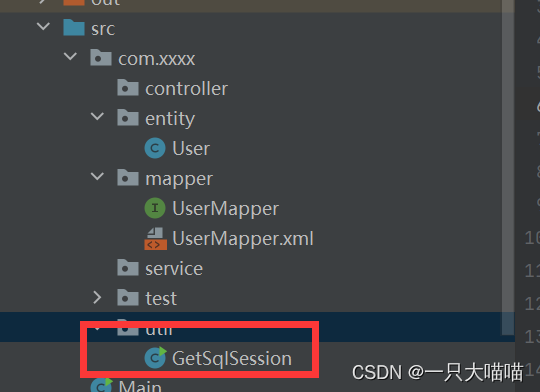
Javaweb增删改查之【查】
Javaweb增删改查之【查】1.前端页面2.java链接数据库——集成mybatis2.1 建立层2.2 实体层entity2.3 mapper(dao层)2.4 mybatis配置文件2.5工具层util3.后台功能3.1servlet前几天跟着b站up主学javaweb登录,突然还是觉得这几年学了c是真的挺好…...

C++ STL:迭代器 Iterator
文章目录1、迭代器的类型2、traitsiterator_traitstype_traits泛化的指针,容器与算法的桥梁。提供一种方法,按照一定顺序访问一个聚合对象中各个元素,而又不暴露该对象的内部表示。既能对容器进行遍历,又可以对外隐藏容器的底层实…...

【C++】泛型编程——模板初阶
文章目录1. 泛型编程2. 函数模板2.1 函数模板的概念2.2 函数模板的使用2.3 函数模板的原理2.4 函数模板的实例化隐式实例化显式实例化2.5 模板参数的匹配原则3. 类模板1. 泛型编程 首先我们来思考一个问题:如何实现一个通用的交换函数呢? 即我们想交换两…...
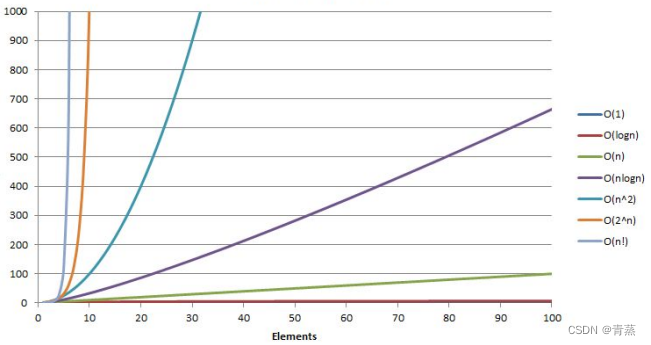
数据结构入门--时间 空间复杂度
数据结构入门 时间 空间复杂度解析 目录 一. 算法效率 二. 时间复杂度 2.1 时间复杂度的概念 2.2 大O的渐进表示法 2.3 题目练习 题目一 题目二 题目三 题目四 题目五 题目六 题目七 三. 空间复杂度 3.1 题目练习 题目一 题目二 题目三 一. 算法效率 算法效率…...
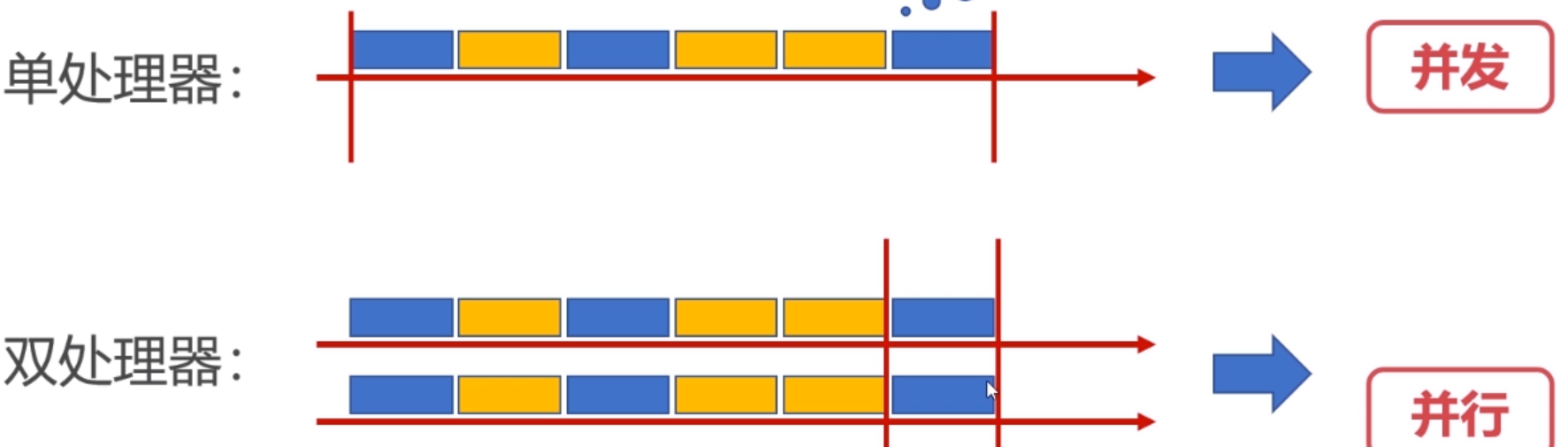
计算机操作系统第一章
操作系统引论1.1操作系统的目标和作用定义:操作系统是控制管理计算机系统的硬软件,分配调度资源的系统软件。目标:方便性,有效性(提高系统资源的利用率、提高系统的吞吐量),可扩充性,…...

ARM LDREX/STREX指令以及独占监控器详解
一、目的Linux驱动开发中有一个特别重要的知识点必须掌握,即并发、竞态以及同步。什么是并发?多个执行单元(进程、线程、中断)同时对一个共享资源的进行访问;此处的共享资源可以是外设、内存或者软件层面的全局变量静态…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
