【代码随想录训练营】【Day25】第七章|回溯算法 |216.组合总和III|17.电话号码的字母组合
组合总和III
题目详细:LeetCode.216
做过上一题组合后,再来写这道题就显得得心应手了,通过理解回溯算法的模版,也总结出了算法中的一些特点:
- 回溯算法与递归算法类似,同样需要参数、结束条件和主体逻辑
- 回溯算法我们可以将它看作是一棵二叉树,树丛根节点到叶子节点的一条路径,就是一个结果:
- 结束条件就相当于遇到了叶子节点,保存当前路径,返回上一层
- for循环相当于是一个选择结构,因为
每个数字最多使用一次 - 同时for循环的次数也决定了树的宽度
- 递归的次数就相当于是for循环的嵌套次数,决定了树的深度
- 每一次递归结束后,都要对结果进行回溯,相当于从叶子节点退回上一个节点,然后继续循环,进入下一条路径,寻找另一个结果
- 从上述回溯过程,我们也可以发现,回溯法类似对树进行深度优先遍历,找出所有的路径,保存符合预期结果的路径,所以本质上也是一种暴力法。
Java解法(回溯,递归):
class Solution {List<List<Integer>> ans = new ArrayList<>();Deque<Integer> path = new ArrayDeque<>();public void backtracking(int k, int n, int sum, int startNum){// 结束条件,叶子节点if(path.size() == k && sum == n){this.ans.add(new ArrayList<>(path));return;}// for循环,选择节点for(int i = startNum; i <= 9; i++){this.path.offer(i);sum += i;// 递归,深度优先遍历backtracking(k, n, sum, i + 1);// 回溯,返回叶子节点的上一节点this.path.removeLast();sum -= i;// 继续循环,进入其他节点,寻找符合结果的路径}}public List<List<Integer>> combinationSum3(int k, int n) {this.backtracking(k, n, 0, 1);return this.ans;}
}
电话号码的字母组合
题目详细:LeetCode.17
这道题我一开始的思路和前两道练习搞混了,琢磨了一个钟之后,看了题解才恍然大悟,原来这道题的不同点是在于在不同集合中找组合。
详细的解释可以看题解:《代码随想录—电话号码的字母组合》
Java解法(递归, 回溯):
class Solution {public List<String> ans = new ArrayList<>();public StringBuffer path = new StringBuffer();public char[][] mapper_all = {{'a','b','c'},{'d','e','f'}, {'g','h','i'}, {'j','k','l'}, {'m','n','o'}, {'p','q','r','s'}, {'t','u','v'}, {'w','x','y','z'}};public List<String> letterCombinations(String digits) {this.backtracking(digits, 0);return this.ans;}public void backtracking(String digits, int startNum){if(path.length() == digits.length()){if(path.length() != 0){ans.add(path.toString());}return;}char[] mapper = mapper_all[digits.charAt(startNum) - '0' - 2];for(int i = 0; i < mapper.length; i++){this.path.append(mapper[i]);// 递归,注意startNum + 1,表示要处理下一个数字了backtracking(digits, startNum + 1);this.path.deleteCharAt(path.length() - 1);}}
}
注意这里for循环,可不像前两天的练习(LeetCode.77和.216)中从startIndex开始遍历的。
因为本题每一个数字代表的是不同集合,也就是求不同集合之间的组合,而之前的练习(LeetCode.77和.216)是求同一个集合中的组合!
相关文章:

【代码随想录训练营】【Day25】第七章|回溯算法 |216.组合总和III|17.电话号码的字母组合
组合总和III 题目详细:LeetCode.216 做过上一题组合后,再来写这道题就显得得心应手了,通过理解回溯算法的模版,也总结出了算法中的一些特点: 回溯算法与递归算法类似,同样需要参数、结束条件和主体逻辑回…...

docker使用
https://blog.csdn.net/u012563853/article/details/125295985http://www.ppmy.cn/news/11249.html启动 docker服务并设置开机自动启动dockersudo systemctl start docker sudo systemctl enable dockerdocker 常见启动失败问题:https://blog.csdn.net/zhulianseu/article/deta…...

手把手docker registry配置登录名/密码
我们的Docker私有仓库Registry服务只有加了认证机制之后我们的Registry服务才会更加的安全可靠。赶快跟随以下步骤来增加认证机制吧。 创建docker registry工作目录 mkdir -p /data/docker.registry 创建将保存凭据的文件夹 mkdir -p /data/docker.registry/etc/registry/auth…...

一步打通多渠道服务场景 中电金信源启移动开发平台MADP功能“上新”
日前,中电金信源启移动开发平台MADP功能迭代升级,“上新”源启小程序开发平台。定位“为金融业定制”的移动PaaS平台,源启小程序开发平台为银行、互联网金融、保险、证券客户提供一站式小程序的开发、运营、营销全生命周期管理技术支撑&#…...
Kubernetes06:Controller (Deployment无状态应用)
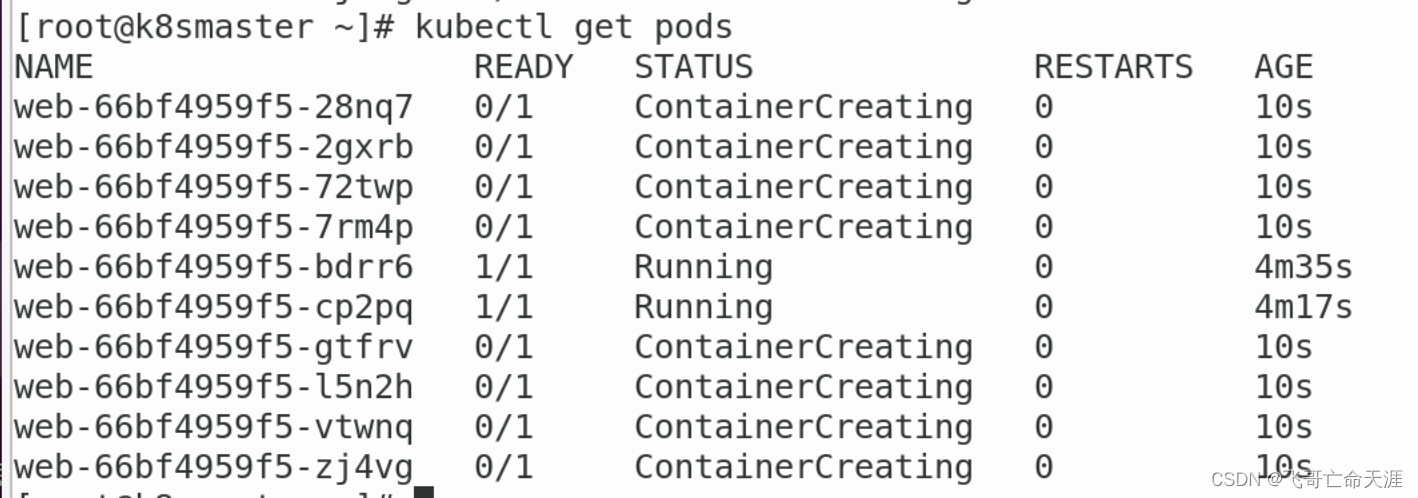
Kubernetes06:Controller 1、什么是controller 管理和运行容器的对象,是一个物理概念 在集群上管理和运行容器的对象 2、Pod和Controller之间的关系 Pod是通过controller来实现应用的运维 比如伸缩、滚动升级等等操作Pod和Controller之间通过 label 标签建立关系…...

低代码开发平台选型必看指南
低代码开发是近年来逐渐兴起的一种新型软件开发方式。它通过封装常见的软件开发流程和代码,使得非专业的开发者也能够轻松创建复杂的应用程序。这种开发方式已经受到了许多企业的青睐,成为提高生产效率、降低开发成本的一种有效途径。 低代码开发的核心…...
OVN:ovn20.03.1/ovs2.13.0编译rpm过程
操作系统openeuler22.0,x86架构分别下载ovn和ovs的源码https://github.com/openvswitch/ovs/tree/v2.13.0https://github.com/ovn-org/ovn/tree/v20.03.1安装必要工具:yum install -y unzip tar make autoconf automake libtool rpm-build gcc libuuid-d…...

Shell管道
一、管道是什么 英文是pipe。 把一个命令的标准输出作为下一个命令的标准输入,以这种方式连接的两个或者多个命令就形成了管道 使用竖线|连接多个命令,称为管道符。 语法格式如下: command1 | command2 [ | commandN... ] command1的标准…...
Zynq UltraScale系列使用MIPI CSI-2 RX Subsystem 解码MIPI视频PD输出 提供2套工程源码和技术支持
目录1、前言2、设计思路和架构3、vivado工程详解4、上板调试验证5、福利:工程代码的获取1、前言 本设计采用OV5640摄像头MIPI模式作为输入,分辨率为1280x72060Hz,MIPI解码方案采用Xilinx官方提供的MIPI CSI-2 RX Subsystem IP解码MIPI视频&a…...

C++:详解C++11 线程休眠函数
休眠函数简介1: 让线程休眠一段时间1.1:std::chrono 的时钟 clock简介 C11 之前并未提供专门的休眠函数,C语言的 sleep、usleep函数其实是系统提供的函数,不同的系统函数的功能还要些差异。 在Windows系统中,sleep的参数是毫秒 …...
TryHackMe-The Great Escape(Docker)
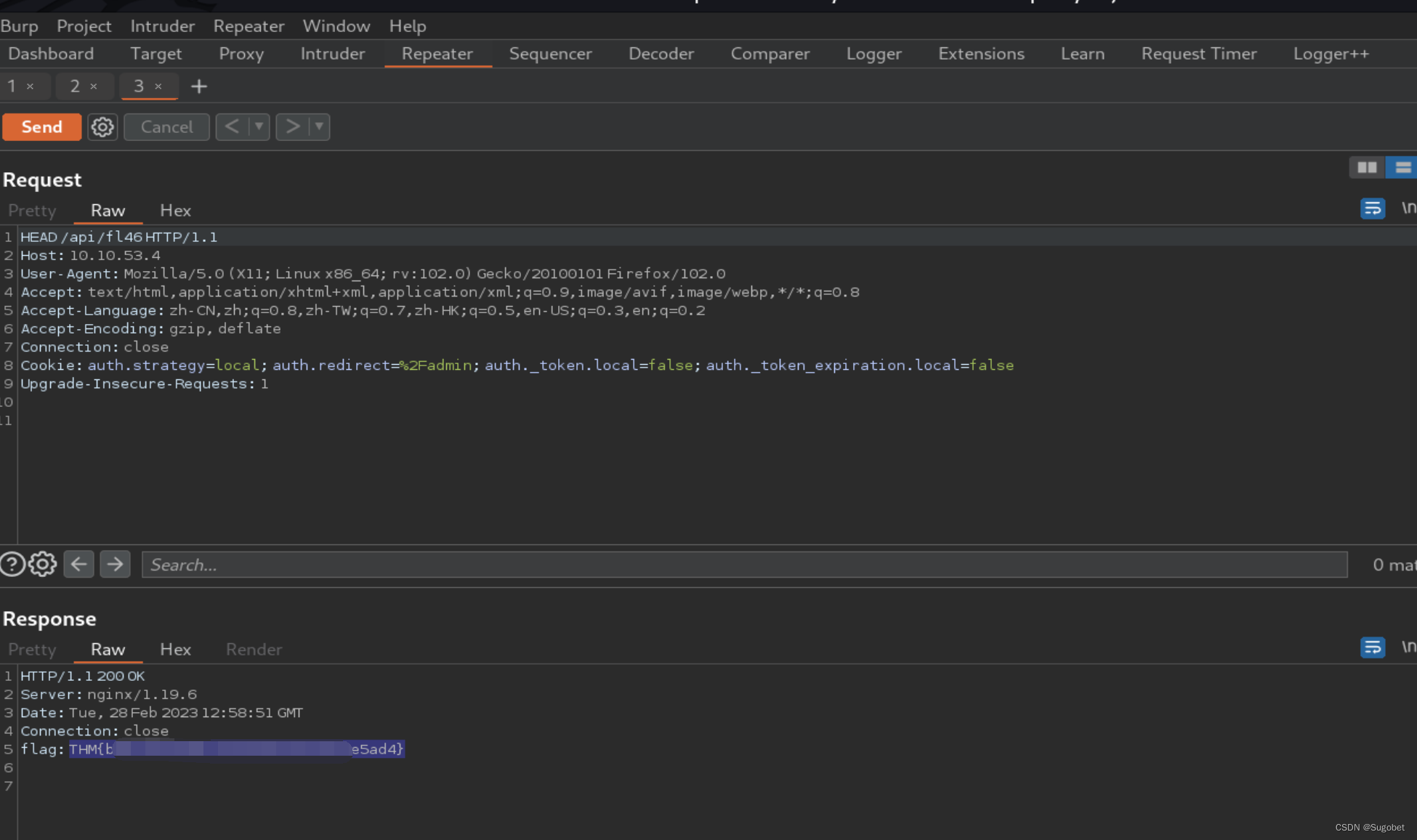
The Great Escape 我们的开发人员创建了一个很棒的新网站。你能冲出沙盒吗? 端口扫描 循例 nmap Web信息收集 robots.txt: /exif-util是文件上传点,但是绕过之后貌似没啥用 在robots.txt当中披露了可能存在.bak.txt,现在我们已知的文件就是…...
这么强才给我28k,我头都不回,转身拿下40k~
时间真的过得很快,眨眼就从校园刚出来的帅气小伙变成了油腻大叔,给各位刚入道的测试朋友一点小建议,希望你们直通罗马吧! 如何选择自己合适的方向 关于选择测试管理: 第一,你一定不会是一个喜欢技术&…...

【Python学习笔记】第二十一节 Python Lambda 函数
Python 提供了非常多的库和内置函数。有不同的方法可以执行相同的任务,而在 Python 中,有个万能之王函数:lambda 函数,它以不同的方式在任何地方使用。一、Lambda 函数简介在 Python 中,函数可以接受一个或多个位置参数…...
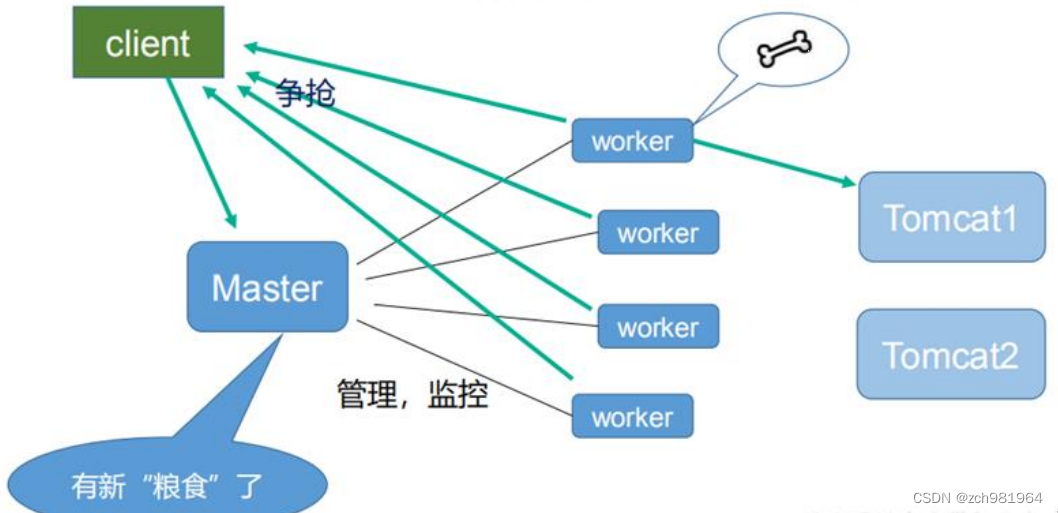
Nginx学习整理
Nginx学习第一章 Nginx概述1.1、Nginx概述1.2、Nginx官网1.3、Nginx用处第二章 Nginx单实例安装2.1、环境说明2.2、安装依赖2.3、Nginx下载2.4、Nginx解压2.5、Nginx安装2.6、Nginx命令2.7、开放防火墙2.8、启动后效果第三章 Nginx正向代理、反向代理3.1、概述3.2、反向代理配置…...

阿里面试之Hr面,这个套路把我坑惨了......
作为技术类的测试工程师面试,往往要经过多次面试才能拿到心仪的offer,这里面有技术一面、二面…,甚至总监面等,还有一个必不可少的就是HR面,一般HR会出现在你面试的最前面和最后面,前面是了解你的基本情况&…...
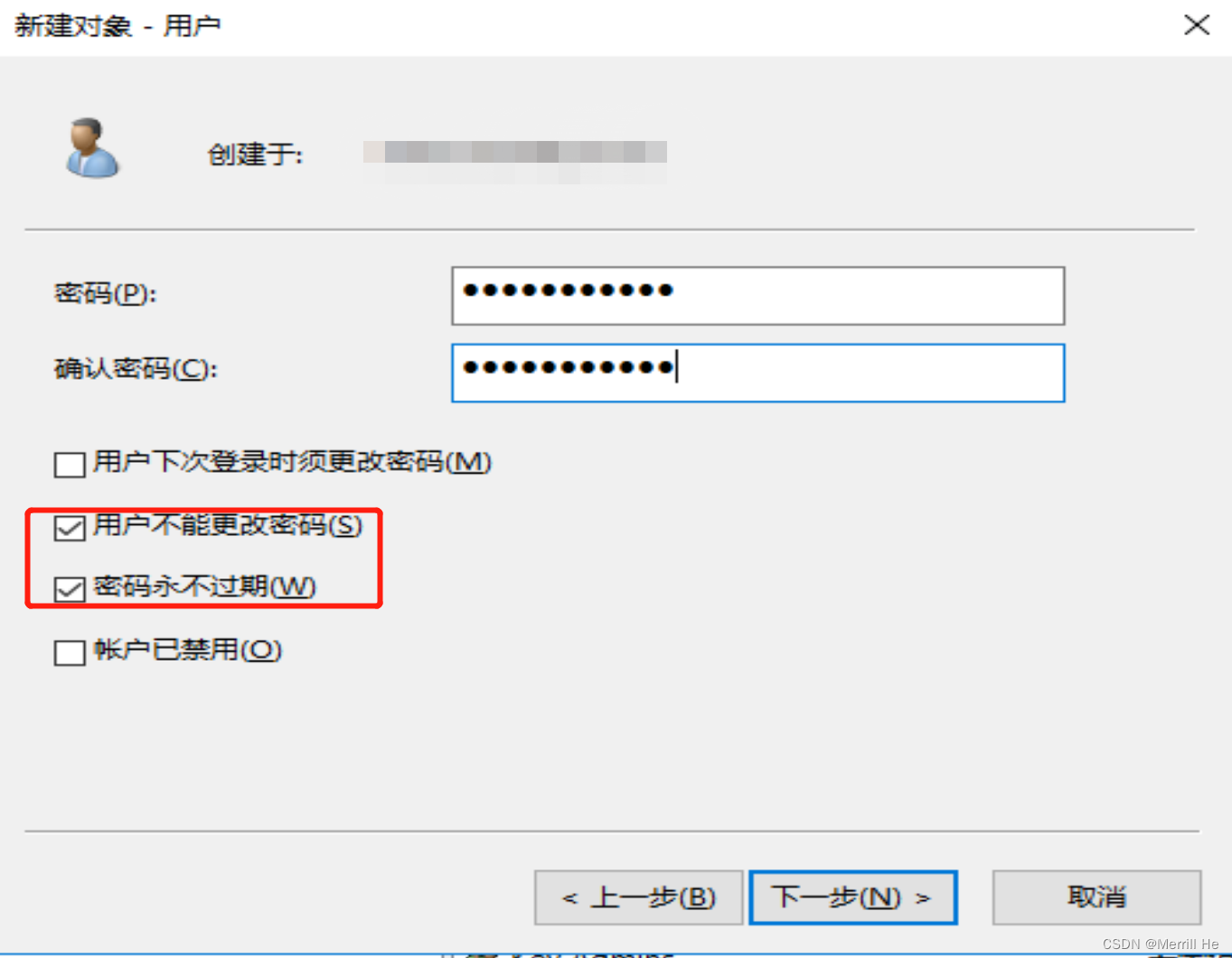
域基础和基本环境搭建
1.1 名词解释 域和工作组的区别: 工作组中所有的计算机都是对等的,也就是没有服务器和客户机的之分,所以工作组并不存在真正的集中管理作用;域是一个有安全边界的计算机集合,安全边界指的是一个域中的用户无法访问到另…...

Java Map集合体系(HashMap、LinkedHashMap、TreeMap、集合嵌套)
目录Map集合体系一、Map集合的概述二、Map集合体系特点三、Map集合常用API四、Map集合的遍历4.1 Map集合的遍历方式一:键找值4.2 Map集合的遍历方式二:键值对4.3 Map集合的遍历方式三:lambda表达式五、Map集合案例-统计投票人数六、Map集合的…...
使用邮箱验证实现登录功能(发送邮件,redis)
目录 概述 前端搭建 后端搭建 生成验证码-存入redis(主要过程代码) 发送邮件(主要过程代码) 登录验证-取出redis中数据进行验证(主要代码) 完整代码一-LoginController 完整代码二-LoginService 完…...

【Linux】网卡的7种bond模式
网卡的7种bond模式 一、bond模式 Mode0(balance-rr) 表示负载分担round-robin,和交换机的聚合强制不协商的方式配合 Mode1(active-backup) 表示主备模式,只有一块网卡是active,另外一块是备的standby,这时如果交换机配的是捆绑,…...
AQS抽象队列同步器
aqs 抽象队列同步器,内部存储了一个valitail修饰的status 和内部类node ,来实现对共享变量并发同步队列机制,以reentrantLock为例,lock底层实际上调用的是sync的lock,会调用cas对status的状态进行修改,来确定是否获得锁…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
