【数据结构】树与二叉树
目录
1、树的概念及结构
1.1、概念
1、树的特点
2、树与非树
1.2、概念 (重要)
1.3、树的表示形式
2、二叉树(重点)
2.1、概念
2.2、二叉树的特点
2.3、两种特殊的二叉树
1、满二叉树
2、完全二叉树
2.4、二叉树的性质
编辑✨ 练习
2.5、二叉树的存储
2.6、二叉树的遍历
2.6.1、前序遍历(先序遍历)
2.6.2、中序遍历
2.6.3、后序遍历
2.6.4、层序遍历
2.6.5、二叉树遍历练习
2.7、二叉树的基本操作
2.7.1、获取树中结点的个数
2.7.2、获取叶子节点的个数
2.7.3、获取第k层结点的个数
2.7.4、获取二叉树的高度
1、树的概念及结构
1.1、概念
树是一种非线性的数据结构,他是由n(n>=0)个有限节点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是跟朝上,而叶朝下的。
1、树的特点
- 有一个特殊的节点,称为跟节点,根节点没有前驱节点
- 除根结点外,其余节点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm,其中每一个集合Ti(1 <= i <= m)又是一棵与树类似的子树。每课子树的根节点有且只有一个前驱,可以有0个或多个后继
- 树是递归定义的。
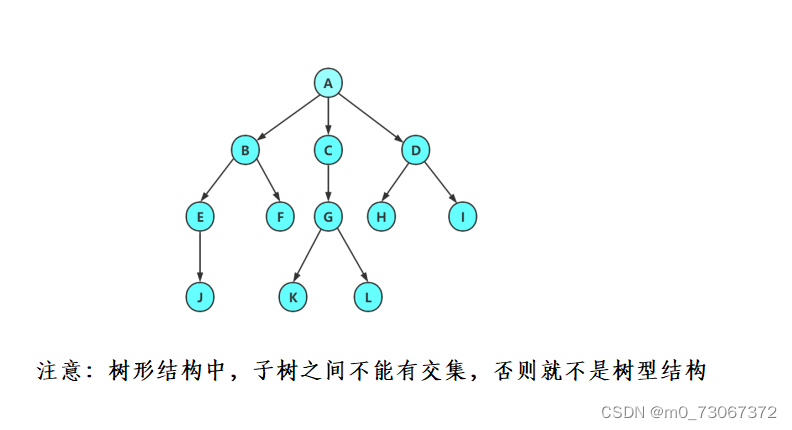
2、树与非树
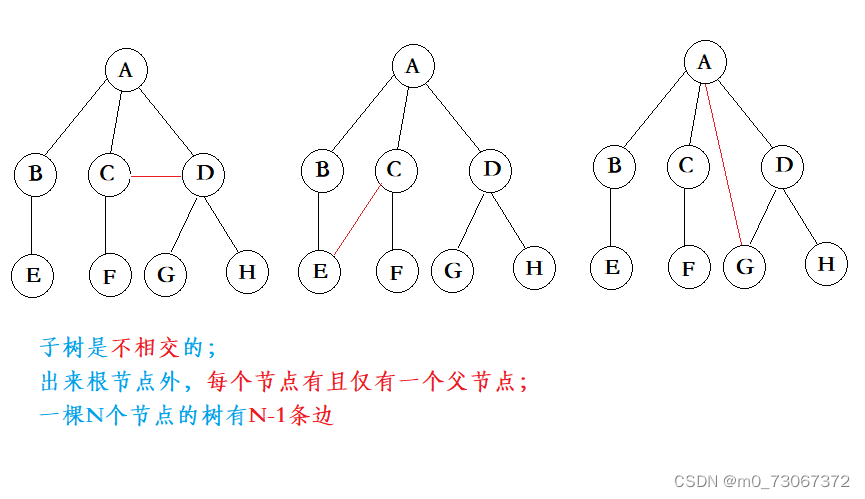
1.2、概念 (重要)
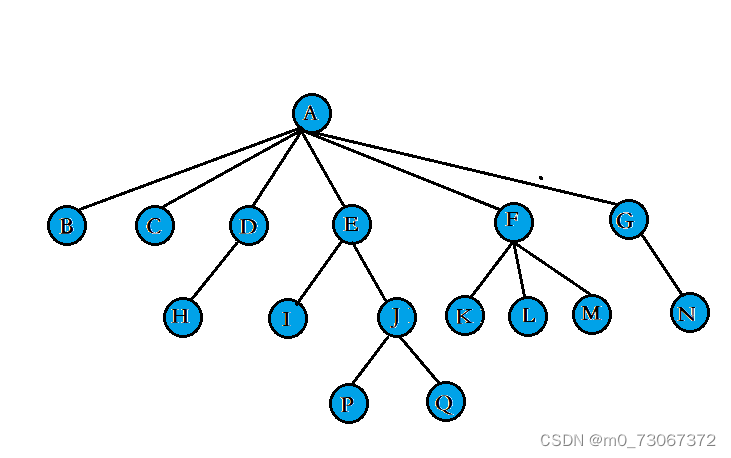
- 结点的度:一个节点含有子树的个数称为该节点的度,也可以理解为节点含有的子节点的个数;如上图:A的度为6。
- 树的度:树内各节点的度的最大值;如上图:树的度为6
- 叶子节点或终端节点:度为0的节点常委叶子节点;如图:B、C、H、I、N、P、Q为叶子节点
- 双亲节点和父节点:若一个节点含有子节点,则这个结点称为其子节点的父节点;如上图:A是B的父节点。
- 孩子结点或子节点:一个结点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子结点
- 根节点:一棵树中,没有双亲结点的结点;如上图:A
- 结点的层次:从根节点定义起,根为第1层,跟的子节点为第2层,以此类推。
- 树的高度或深度:树中结点的最大层次;如上图:树的高度为4
以下概念只需了解,在看书的时候知道是什么意思即可
- 非终端结点或分支结点:度不为0的结点;如上图:D、E、F、G、J为分支结点
- 兄弟结点:具有相同父节点的结点互称为兄弟节点;如上图:B、C是兄弟结点
- 堂兄弟结点:双亲正在同一层的结点互为堂兄弟;如上图:H、I互为堂兄弟结点
- 结点的祖先:从根到该节点所经分支上的所有结点;如上图:A是所有结点的先祖
- 子孙:以某结点为根的子树中任一结点都称为该节点的子孙。如上图:所有结点都是A的子孙
- 森林:有m(m >= 0) 棵互不相交的树组成的集合称为森林。对树中每个结点而言,其子树的集合几位森林。
1.3、树的表示形式
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法、孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。这里我们就简单的了解其中最常用的孩子兄弟表示法。
class Node {int value; // 树中存储的数据Node firstChild; // 第一个孩子引用Node nextBrother; // 下一个兄弟引用
}
2、二叉树(重点)
2.1、概念
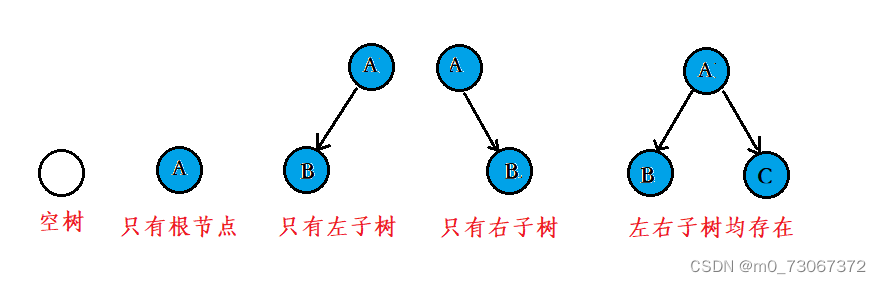
二叉树是结点的一个有限集合,该集合:
- 或者为空;
- 或者是由一个根结点加上两颗分别称为左子树和右子树的二叉树组成。

2.2、二叉树的特点
- 每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点。注意不是只有两棵子树,而是最多有。该节点没有子树或者有一颗子树都是可以的。
- 左子树和右子树是有顺序的,次序不能任意颠倒,因此二叉树是有序树。
- 即使树中某个节点只有一棵子树,也要区分它是左子树还是右子树。
2.3、两种特殊的二叉树
1、满二叉树
定义(两种方式)
- 在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
- 一棵二叉树,如果每层的结点数都达到最大值,则这颗二叉树就是满二叉树
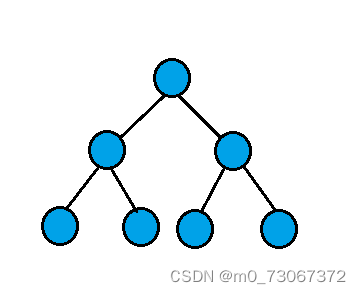
单是每个结点都存在左右子树,不能算是满二叉树,还必须要所有的叶子都在通一层上,这就做到了整棵树的平衡。
满二叉树的特点
- 叶子只能出现在最下一层。出现在其他层就不可能达成平衡。
- 非叶子结点的度一定是2.否则就是"去胳膊少腿"了。
- 在同一深度的二叉树中,满二叉树的结点个数最多,叶子树最多。
- 如果一棵满二叉树的层数为k,则它的结点总数是
.
2、完全二叉树
✨定义:
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1<i<n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这颗二叉树称为完全二叉树。
❗❗❗可以这样理解:
完全二叉树的所有结点与同样深度的满二叉树,他们按层序编号。两个二叉树中的节点编号是一一对应的。满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
画图理解

✨ 完全二叉树的特点
- 叶子结点只能出现在最下两层
- 最下层的叶子一定集中在最左部连续位置
- 倒数第二层,若有叶子节点,一定是在右部连续位置
- 如果结点的度为1,则该结点只有左孩子,即不存在只有右子树的情况
- 同样节点数的二叉树,完全二叉树的深度最小
2.4、二叉树的性质
1、若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有(i > 0)个结点
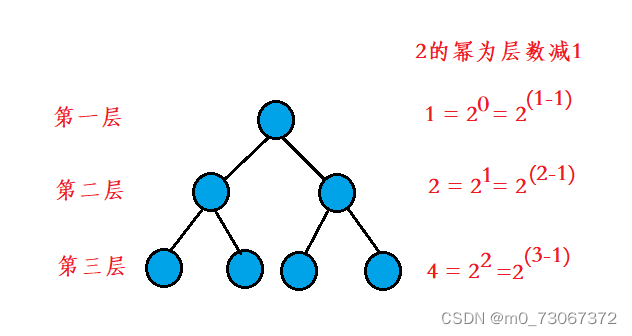
2、若规定只有根节点的二叉树的深度为1,则深度为K的二叉树的最大节点数是(k >= 0)

3、对任何一棵二叉树,如果其叶子结点个数为n0,度为2的非叶子结点个数为n2,则有n0 = n2+1
论证:
通过学习树的知识,我们知道一棵N个结点的树有N-1条边 。
这条性质的意思是,任何一个二叉树中,度为0的结点比度为2的结点多1个

4、具有n个结点的完全二叉树的深度k = 向上取整。
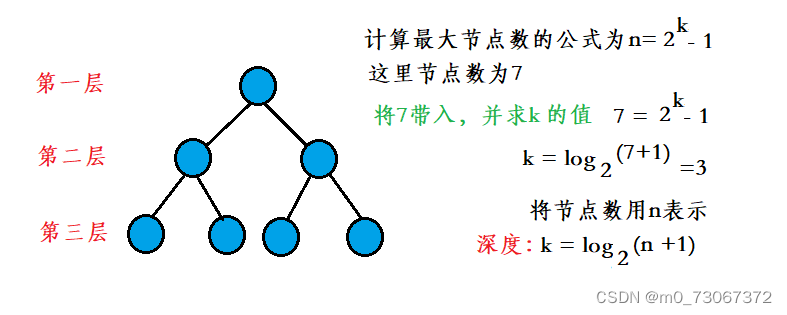
5、 对于有n个结点的完全二叉树,如果按照从上至下、从左至右的顺序对所有结点从0开始编号,则对于序号为i的结点有:
- 若 i > 0,双亲序号:(i-1)/2;i = 0,i为根结点编号,无双亲结点
- 若2i+1 < n,左孩子序号:2i+1,否则无左孩子
- 若2i + 2 < n,有孩子序号,否则无右孩子
 ✨ 练习
✨ 练习
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为(B )
A 、不存在这样的二叉树 B、200 C、198 D、199
❗题解:叶子结点也就是度为0的结点,已知度为2的结点为199个,根据公式n0 = n2 + 1;得度为0的结点为200个。
2、在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )
A n B n+1 C n-1 D n/2
❗题解:
3.一个具有767个节点的完全二叉树,其叶子节点个数为(B)
A 383 B 384 C 385 D 386
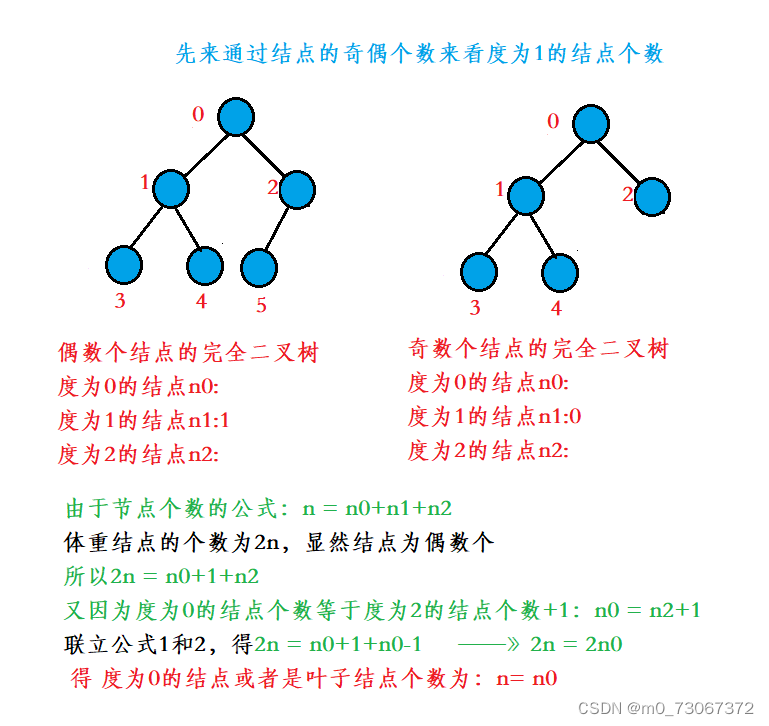
❗题解:由于结点的个数为奇数,所以根据公式n = n0+n1+n2——》767 = n0+n2得公式1
再由度为0的节点数等于度为2的节点数+1:n0 = n2+1 得公式2
联立公式1和2得:767 = n0+n0-1 ——》768 = 2n0 ——》n0 = 384
故:叶子节点个数为384,所以选B
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为( B)
A 11 B 10 C 8 D 12
题解: n个结点的完全二叉树的深度为k =
(向上取整)
所以k =
,2^9 = 512,说明9层放不下所有结点,向上取整
所以这棵树的高度为10
2.5、二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
二叉树的链式存储是通过一个一个的结点引用起来的,常见的表示方式由二叉和三叉表示方式。
// 孩子表示法
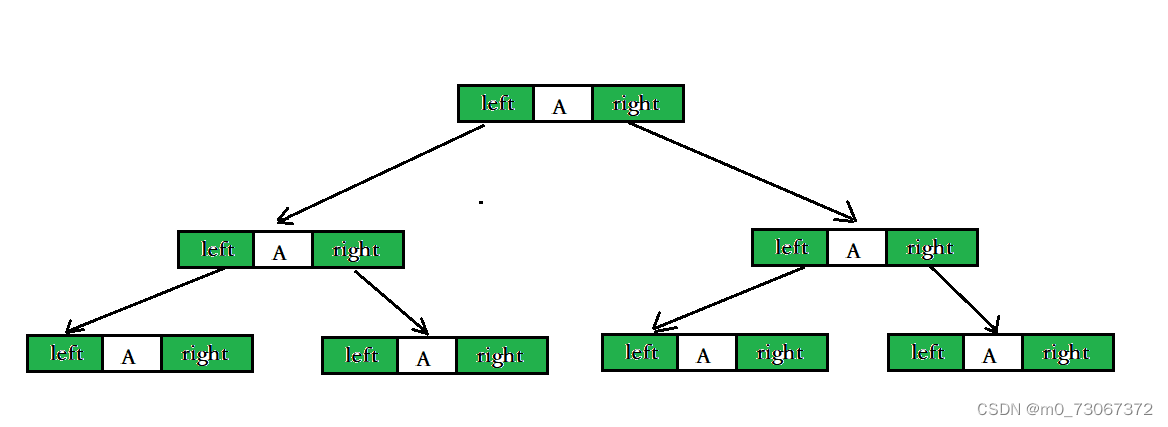
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}本章博客主要了解孩子表示法
2.6、二叉树的遍历
在学习二叉树的遍历以及后续的二叉树的基本操作的时候,首先要生成一个二叉树,但是生成一个二叉树需要用到递归,有些难度,这里我们手动创建一个二叉树,方便二叉树的遍历和基本操作方法的学习。
public class TestbinaryTree {//定义二叉树的类static class TreeNode{//定义结点public char val;public TreeNode left;//孩子结点,所以用TreeNode类型的引用public TreeNode right;public TreeNode(char val){this.val = val;}}public TreeNode root;//每个二叉树都有一个根节点public TreeNode createTree(){//通过调用这个方法来创建一个二叉树,不用担心在这个方
//法中创建了二叉树是局部变量,出了这个方法之后,创建的二叉树被回收,因为每个结点都被引用了TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;E.right = H;this.root = A;return root;}}
学习二叉树最简单的方式就是遍历。所谓遍历是指沿着某条搜索路线,依次对树中每个结点均作一次且仅作一次访问。访问结点所作的操作依赖于具体的引用问题 (比如:打印结点内容、节点内容加1).遍历时二叉树上最重要的操作之一,时二叉树上进行其他运算的基础。
2.6.1、前序遍历(先序遍历)
前序遍历 :访问根节点——》根的左子树——》根的右子树。
✨遍历流程:
- 先遍历二叉树的根节点,若根节点A不为空,打印根节点A。
- 再遍历根节点的左子树B,若左子树的根节点B不为空,打印B。
- 再遍历B结点的左子树D,若左子树的根节点D不为空,打印D;为空,打印D,返回到D结点的根节点B。
- 遍历B结点的右子树,输出根节点的值。
- 依次为例,将整棵树遍历完成,每个结点只输出一次 。
- 每次输出的都是树的根节点。

✨代码示例 :这里有两种思路:遍历思路和子问题思路
写法一:遍历的思路(好理解)
//前序遍历:根——》左子树——》右子树public void preOrder(TreeNode root){if(root == null){//递归的开始也是结束条件return ;//若根节点为空,则直接返回}System.out.println(root.val+" ");//若根不为空,先输出跟结点preOrder(root.left);//通过调用自己,实现递归,遍历左子树preOrder(root.right);}
✨递归过程 :
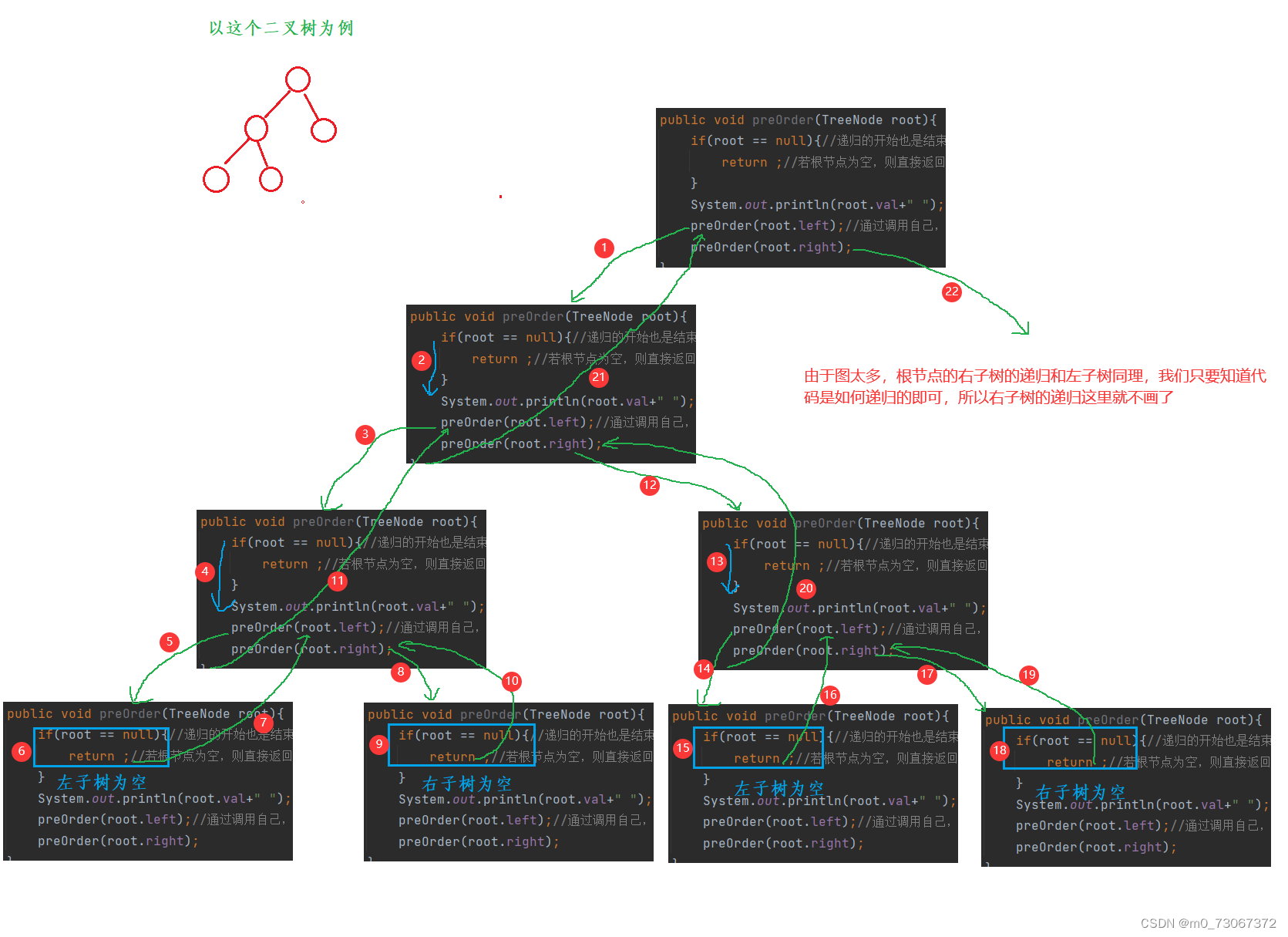
写法二 :子问题思路(难理解)
1.这个代码还是存在很多问题的,给了返回值类型,但是并没有将该方法的返回值用起来
List<Integer> ret = new ArrayList<>();//用来记录遍历的结点的值public List<Integer> preorderTraversal(TreeNode root){if(root == null){return ret;//根节点为空,返回ret;}ret.add(root.val);//将根节点的值,放到ret当中preorderTraversal(root.left);//遍历左子树preorderTraversal(root.right);//遍历右子树return ret;}2、这个是子问题思路比较合理的写法。
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> ret = new ArrayList<>();//每次调用这个方法,都会产生新的空间,用来记录这个方法遍历的内容if (root == null) {return ret;//根节点为空,返回ret;}ret.add(root.val);//将二叉树的根节点的值,放到ret当中//将左子树遍历到的内容放到左子树的数组中List<Integer> leftTree = preorderTraversal(root.left);//遍历左子树,并用List<Integer>类型的引用来接收方法的返回值ret.addAll(leftTree);//addAll方法用来向ret集合中添加一个集合对象所包含的所有内容//将右子树遍历到的内容放到右子树的数组中List<Integer> rightTree = preorderTraversal(root.right);//遍历右子树ret.addAll(rightTree);return ret;}2.6.2、中序遍历
中序遍历:根的左子树——》根节点——》根的右子树
✨遍历流程
- 先遍历二叉树的左子树,若根节点A不为空,遍历A的左子树B.
- 若B不为空,遍历他的左子树D,若D的左子树为空,则返回输出D,
- 再遍历右子树,若右子树为空,则B的左子树遍历完成,返回到B,并输出B。
- 再遍历B的右子树,若为空,则A的左子树遍历完成,返回输出A,
- 再遍历A的右子树,
- 以此为例,知道整棵树遍历完成。

✨代码示例 :
1、遍历的思路
//中序遍历:左子树——》根节点——》右子树public void inOrder(TreeNode root){if(root == null){//递归的开始和结束条件return;//若根节点为空,则返回}inOrder(root.left);//若根节点不为空,则递归左子树System.out.println(root.val+" ");//左子树递归完成,打印根节点inOrder(root.right);//再递归右子树}中序遍历的代码递归过程,就不再演示了,思路前序遍历相似。
2、子问题思路
public List<Character> inOrder(TreeNode root) {List<Character> ret = new ArrayList<>();//每次调用这个方法,都会产生新的空间。if (root == null) {return ret;//根节点为空,返回ret;}//将左子树遍历到的结点的内容放到左子树的数组中List<Character> leftTree = inOrder(root.left);//遍历左子树,并用List<Integer>类型的引用来接收方法的返回值ret.addAll(leftTree);//addAll方法用来向ret集合中添加一个集合对象所包含的所有内容ret.add(root.val);//将二叉树的第一个根节点的值,放到ret当中//将右子树遍历到的结点的内容放到左子树的数组中List<Character> rightTree = inOrder(root.right);//遍历右子树ret.addAll(rightTree);return ret;}2.6.3、后序遍历
后序遍历:根的左子树——》根的右子树——》根节点
✨遍历流程
- 先遍历二叉树的左子树,若跟结点A不为空,则遍历A的左子树B。
- 若B不为空,则遍历B的左子树D。
- 若D不为空,则遍历D的左子树,若D的左子树为空,则返回到D,再遍历D的右子树。
- 若D的右子树为空,则返回输出根节点D,则B的左子树就遍历完成,返回到B,再遍历B的右子树。
- 若B的右子树为空,则返回B,并输出A的左子树B,再返回A,再遍历A的右子树C。
- 以此为例。直到遍历完整棵树。
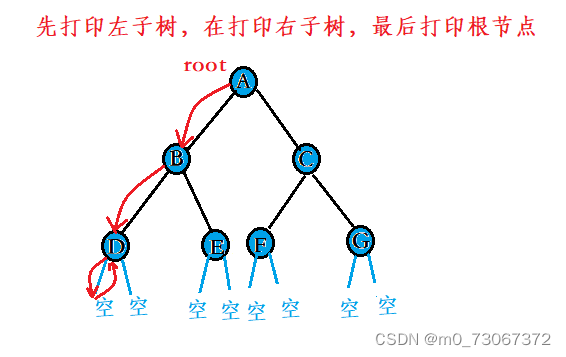
✨代码示例
1、遍历思路
//后序遍历:左子树——》右子树——》根节点public void postOrder(TreeNode root){if(root == null){//递归的开始和结束条件return;//若根节点为空,则返回}postOrder(root.left);//若根节点不为空,则递归左子树postOrder(root.right);//再递归右子树System.out.println(root.val+" ");//左右子树都递归完成,打印根节点}2、子问题思路
public List<Character> postOrder(TreeNode root) {List<Character> ret = new ArrayList<>();//每次调用这个方法,都会产生新的空间。if (root == null) {return ret;//根节点为空,返回ret;}//将左子树遍历到的结点的内容放到左子树的数组中List<Character> leftTree = postOrder(root.left);//遍历左子树,并用List<Integer>类型的引用来接收方法的返回值ret.addAll(leftTree);//addAll方法用来向ret集合中添加一个集合对象所包含的所有内容//将右子树遍历到的结点的内容放到左子树的数组中List<Character> rightTree = postOrder(root.right);//遍历右子树ret.addAll(rightTree);ret.add(root.val);//将二叉树的第一个根节点的值,放到ret当中return ret;}✨遍历测试
以createTree中手动生成的树为例:前序遍历:ABDEHCFG;中序遍历:DBEHAFCG;后序遍历:DHEBFGCA。与测试结果相同。
public class Test {public static void main(String[] args) {TestbinaryTree testbinaryTree = new TestbinaryTree();TestbinaryTree.TreeNode root = testbinaryTree.createTree();System.out.println("==前序遍历==");testbinaryTree.preOrder(root);System.out.println();System.out.println("==中序遍历==");testbinaryTree.inOrder(root);System.out.println();System.out.println("==后序遍历==");testbinaryTree.postOrder(root);System.out.println();}}
2.6.4、层序遍历
设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根结点,然后从左到右访问第二层上的结点,接着是第三层的结点,以此类推,自上而下,自左至右逐层访问数的结点的过程就是层序遍历。

2.6.5、二叉树遍历练习
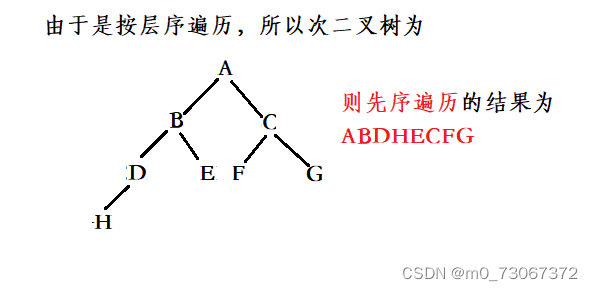
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为(A)
A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA
【题解】
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为(A)
A: E B: F C: G D: H
【题解】
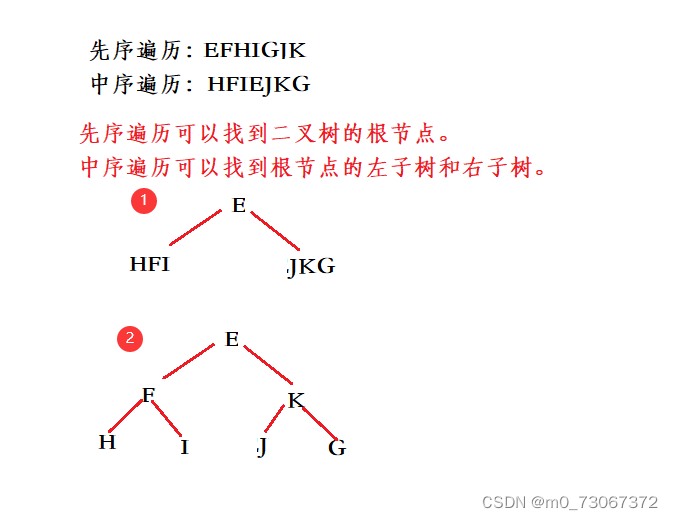
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为(D)
A: adbce B: decab C: debac D: abcde
【题解】

4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为(A)
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
【题解】
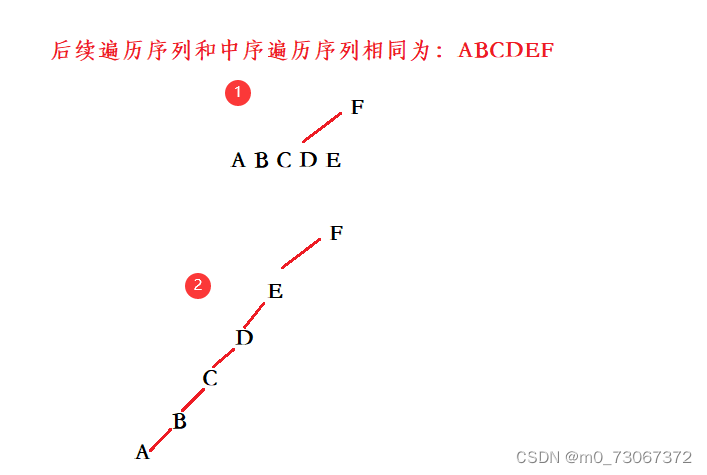
❗❗❗ 总结:
- 当前序遍历序列和中序遍历序列同时知道,可以得到后续遍历序列。
- 当中序遍历序列和后序遍历序列同时知道,可以得到前序遍历序列。
- 但是当后序遍历序列和前序遍历序列同时知道,不能得到中序遍历序列。
- 前序遍历序列和后序遍历序列可以知道二叉树的根节点,中序遍历序列可以知道根节点的左右子树。
2.7、二叉树的基本操作
2.7.1、获取树中结点的个数
这个方法的递归公式可以用子问题思路来思考。
左子树结点个数+右子树结点个数+根节点 = 总节点数
当有左子树和右子树则用上述的公式,若没有则可以直接输出根节点1.
【代码示例】
1、子问题思路:
public int size(TreeNode root){if(root == null){return 1;}int leftSize = size(root.left);//这里的递归,每次走左边结点,查看子树的左右结点,然后将子树的左右结点加根节点的值返回。int rightSize = size(root.right);return leftSize + rightSize + 1;}2、遍历思路
每个结点都是一个子树的根节点,当根节点不为空时,则+1
public int nodeSize;public void size1(TreeNode root){if(root == null){return ;}nodeSize++;size1(root.left);size1(root.right);}❗❗❗这个方法存在一个问题,当有两个二叉树都要求结点个数时,引用第一次结果是正确的,但是第二次就会出错,因为nodeSize 属性是属于某个引用的,在test类当中用同一个引用调用两次这个方法,那么第二次nodeSize的结果是将两个树中的结点都加在了一起。
❗❗❗总结:这个方法的时间复杂度为:O(N)
空间复杂度为O(logN) ,原因在于二叉树的遍历是先遍历左子树再遍历右子树,所以再极端情况下,他能开辟的空间就是树的高度。
2.7.2、获取叶子节点的个数
❗❗❗思路:
- 当一个二叉树的结点的左右子树都为空,则这个结点就是二叉树的叶子结点。
- 所以当根节点为空时,二叉树为空,返回0,
- 当根节点不为空时,且二叉树中某个结点的左右子树都为空时,则这个结点为叶子节点,返回1
✨代码示例
1、子问题思路
public int getLeafNodeCount(TreeNode root){if(root == null){return 0;}if(root.right == null&&root.left == null){//这里判断是叶子节点,记录一个结点1.return 1;}//这两个if条件作为递归的结束条件int leftSize = getLeafNodeCount(root.left);int rightSize = getLeafNodeCount(root.right);return leftSize+rightSize;//将左右两个子树的叶子结点加起来}2、遍历思路
public int leafSize;public void getLeafNodeCount2(TreeNode root){if(root == null){return;}if(root.left == null&&root.right == null){leafSize++;//遍历一个叶子节点+1}getLeafNodeCount2(root.left);//调用该方法遍历左子树。getLeafNodeCount2(root.right);}2.7.3、获取第k层结点的个数
以下面的二叉树为例,第k = 3层的结点的个数。
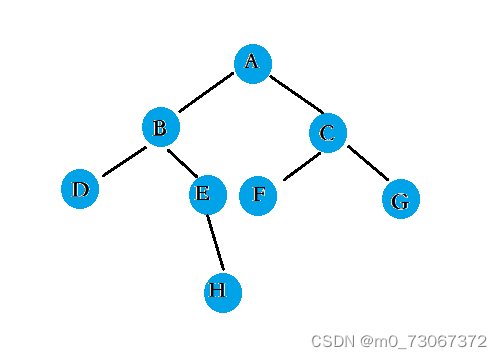
✨子问题思路:
当要求A树的第3层结点个数时,则要求A树的左子树B的k-1层结点个数和A树的右子数C的k-1层结点个数的合。
✨代码示例
//获取第k层结点的个数public int getLevelNodeCount(TreeNode root,int k){if(root == null){return 0;}if(k == 1){return 1;}int leftSize = getLevelNodeCount(root.left,k-1);int rightSize = getLevelNodeCount(root.right,k-1);return leftSize+rightSize;}
2.7.4、获取二叉树的高度
以下列的二叉树为例
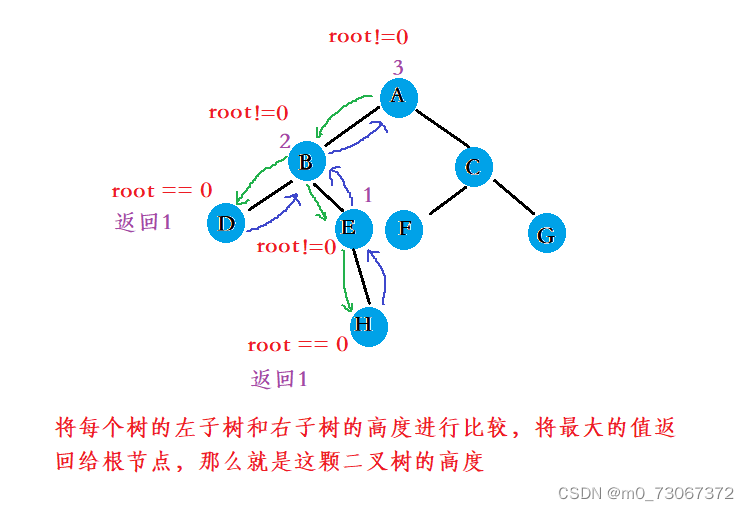
✨子问题思路
- 每次遍历的都是树的根节点,当根节点为空时,递归结束。
- 那么左子树的高度也就确定。
- 以同样的方式遍历右子树,确定右子树的高度
- 再将两个树的高度进行比较,最大的高度+1就是该二叉树的高度。
✨代码示例
//获取二叉树的高度public int getHeight(TreeNode root){if(root == null){return 0;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return (leftHeight>rightHeight)?(leftHeight+1):(rightHeight+1);}相关文章:

【数据结构】树与二叉树
目录 1、树的概念及结构 1.1、概念 1、树的特点 2、树与非树 1.2、概念 (重要) 1.3、树的表示形式 2、二叉树(重点) 2.1、概念 2.2、二叉树的特点 2.3、两种特殊的二叉树 1、满二叉树 2、完全二叉树 2.4、二叉树的性…...
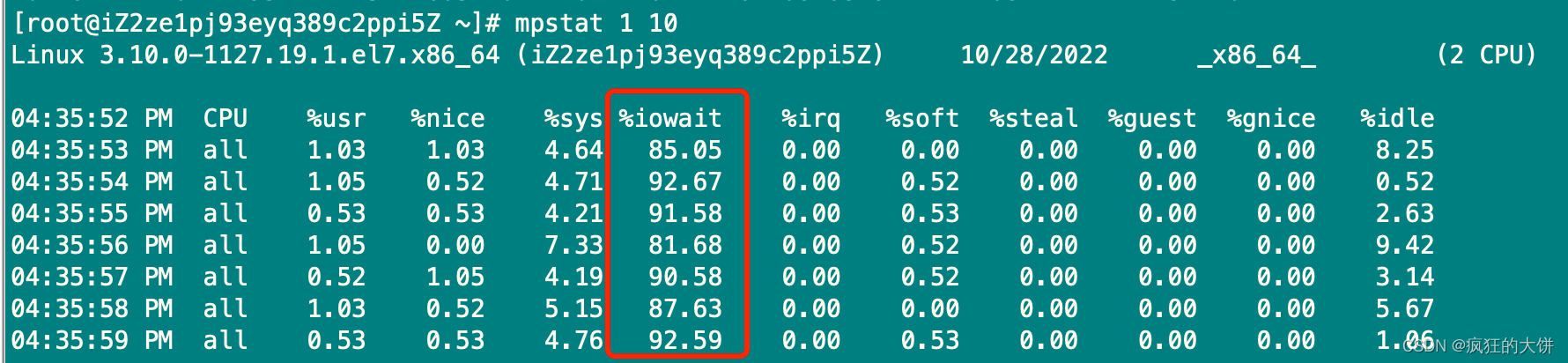
Stress压力工具的部署及使用
Stress压力工具的部署及使用 下载地址:wget https://fossies.org/linux/privat/old/stress-1.0.5.tar.gz 1.部署 进入目录执行./autogen.sh [rootiZ2ze1pj93eyq389c2ppi5Z stress-1.0.5]# ./autogen.sh ps:如果执行过程中缺包,安装对应的…...

[蓝桥杯 2020 省 AB3] 乘法表
题目描述九九乘法表是学习乘法时必须要掌握的。在不同进制数下,需要不同的乘法表。例如, 四进制下的乘法表如下所示:1*11 2*12 2*210 3*13 3*212 3*321请注意,乘法表中两个数相乘的顺序必须为样例中所示的顺序,不能随意交换两个乘…...

Python基础知识
基础知识 基础知识包括输入输出、变量、数据类型、表达式、运算符这5个方面。 1.输入输出 Python有很多函数,后面我们会细讲,但这里先将两个最基本的函数:输入和输出。 输出函数print(),在前面我们已经用过了,语法…...

FME案例实战教程:聚焦实战应用,摆脱思路束缚,您值得拥有
一、教程链接(一)FME案例实战教程链接1.FME案例实战教程(完整版) ☚强烈推荐☚2.FME案例实战教程(A组)3.FME案例实战教程(B组)4.FME案例实战教程(C组)&#…...
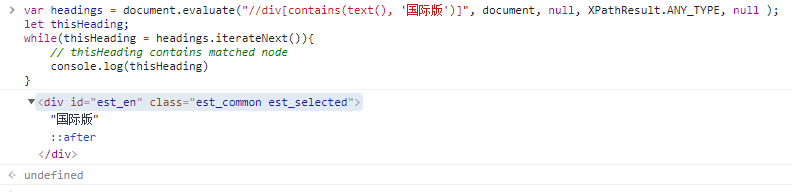
【JavaScript】根据元素内容遍历元素的方案
▒ 目录 ▒🛫 导读需求1️⃣ jQuery2️⃣ XPATH(document.evaluate)3️⃣ 原生js(querySelectorAll & Array)🛬 文章小结📖 参考资料🛫 导读 需求 因业务需要,根据元…...
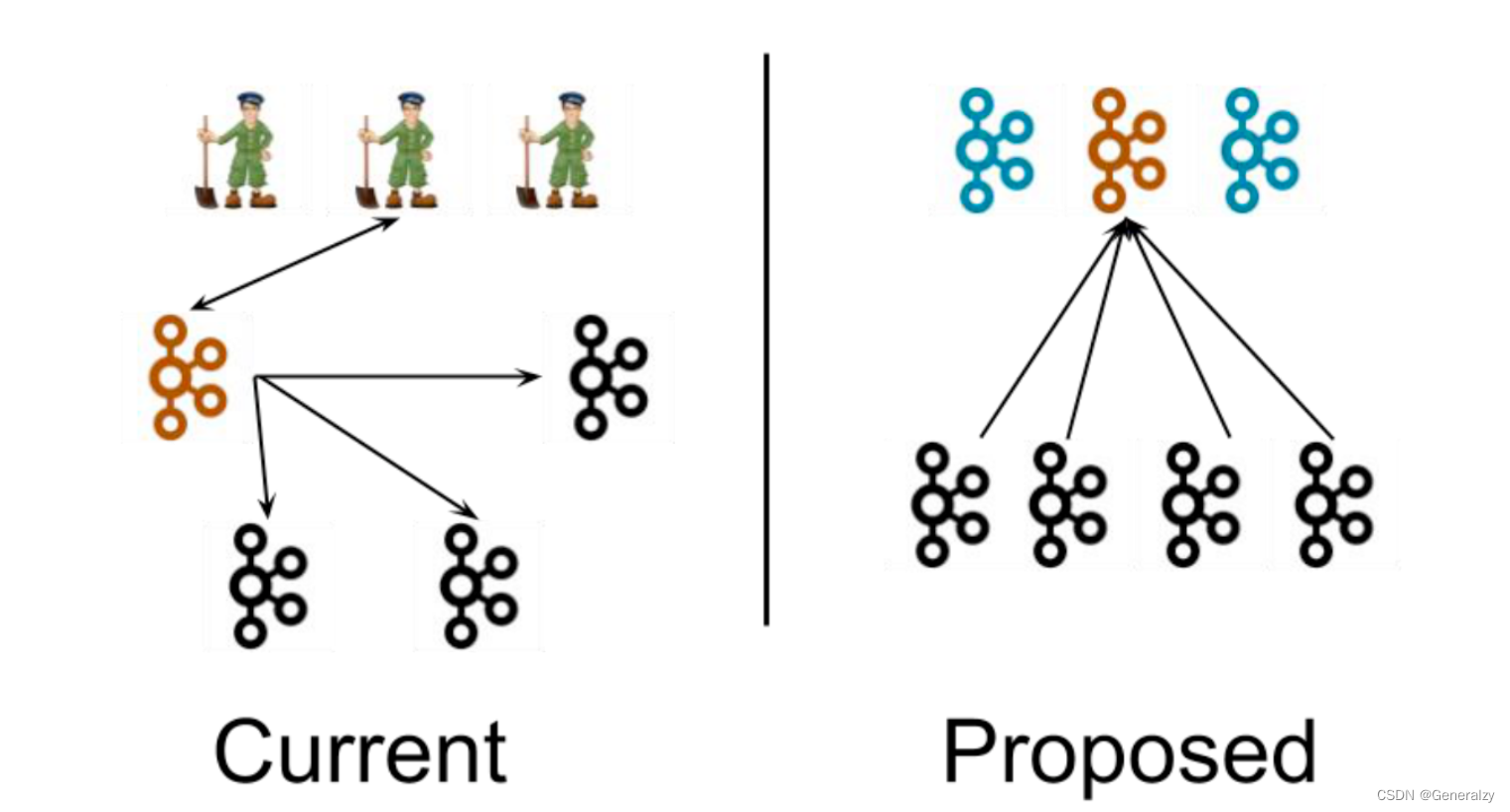
kafka全解
目录Kafka概述定义消息队列目录结构分析传统消息队列的应用场景消息队列的两种模式点对点模式发布/订阅模式Kafka基础架构Kafka快速入门安装部署集群规划集群部署集群启停脚本Kafka命令行操作Kafka基础架构主题命令行操作生产者命令行操作消费者命令行操作kafka可视化工具Kafka…...

(三)随处可见的LED广告屏是怎么工作的呢?接入GUI
续上文,本篇我们将尝试接入一个GUI来控制点阵屏。在前两篇中,我们相继介绍了点阵屏的控制原理,以及如何让点阵屏按照我们所想的进行显示。本篇将在此基础上接入一个GUI,使点阵屏的控制更加优雅。限于阅读体验和展示效果࿰…...

线程池简介
线程池 线程池(英语:thread pool):一种线程使用模式。线程过多会带来调度开销,进而影响缓存局部性和整体性能。而线程池维护着多个线程,等待着监督管理者分配可并发执行的任务。这避免了在处理短时间任务时…...

大数据面试题集锦-Hadoop面试题(四)-YARN
你准备好面试了吗?这里有一些面试中可能会问到的问题以及相对应的答案。如果你需要更多的面试经验和面试题,关注一下"张飞的猪大数据分享"吧,公众号会不定时的分享相关的知识和资料。 文章目录1、为什么会产生 yarn,它解决了什么问题…...
Python---time模块
专栏:python 个人主页:HaiFan. 专栏简介:Python在学,希望能够得到各位的支持!!! time模块前言时间戳time.time()将时间戳转换成字符串time.ctime()将时间戳转换为元组time.localtime(时间戳)将元…...

坚鹏:学习贯彻二十大精神 解码共同富裕之道(面向银行)
学习贯彻二十大精神 解码共同富裕之道课程背景: 很多银行从业人员存在以下问题:不知道如何准确解读二十大精神?不清楚共同富裕相关政策要求?不知道如何有效推动共同富裕? 课程特色:有实战案例有…...

python查看程序的cpu和内存资源占用情况
1.获取线程消耗的内存 :线程内存使用的概念没有明确定义。线程共享它们的内存。唯一真正的线程本地内存是它的调用堆栈,除非您认真地递归地做一些事情,否则这不是有趣的部分。 2.获取进程消耗的内存 3.获取程序消耗的内存 mprof run endpoint.py 4.查看…...
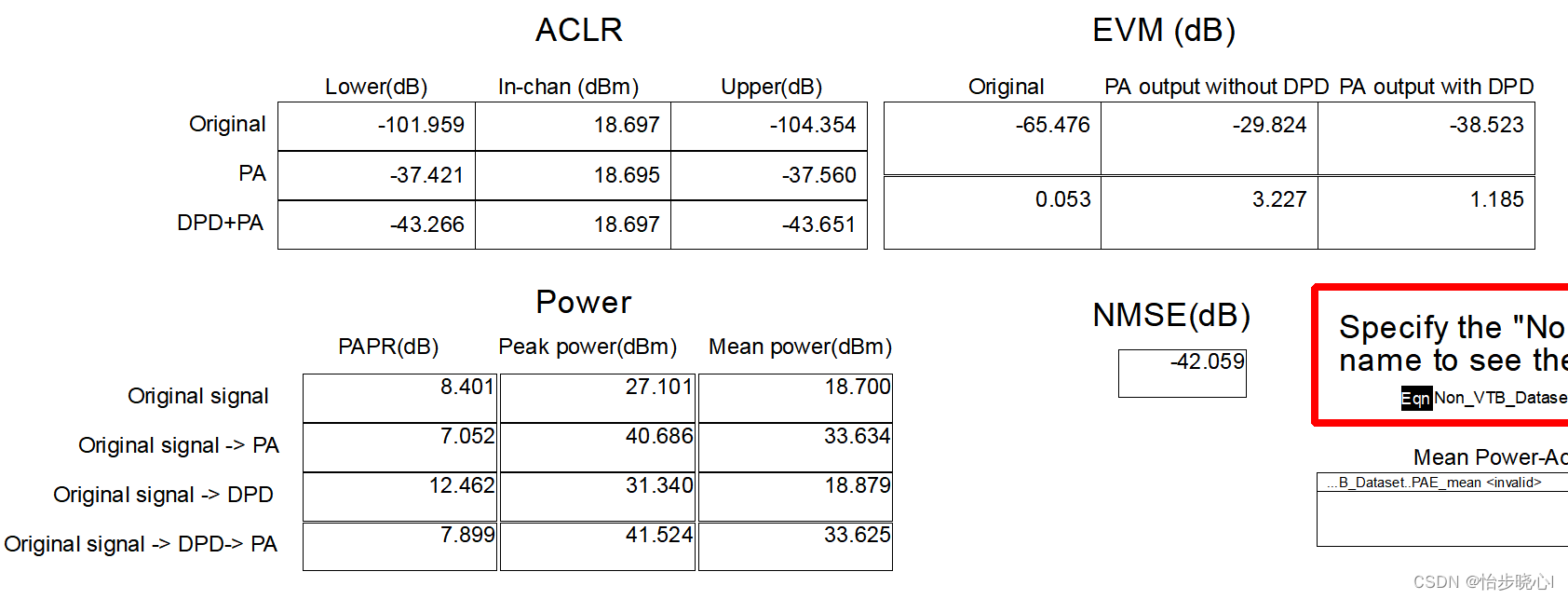
番外10:使用ADS对射频功率放大器进行非线性测试2(使用带宽20MHz的64QAM信号进行ACLR、EVM、CCDF测试)
番外10:使用ADS对射频功率放大器进行非线性测试2(使用带宽20MHz的64QAM信号进行ACLR、EVM、CCDF测试) 1、基本理论 功率放大器的非线性性能十分重要,特别是对于当前广泛使用的移动设备。由于其各种复杂的信号调制,功…...
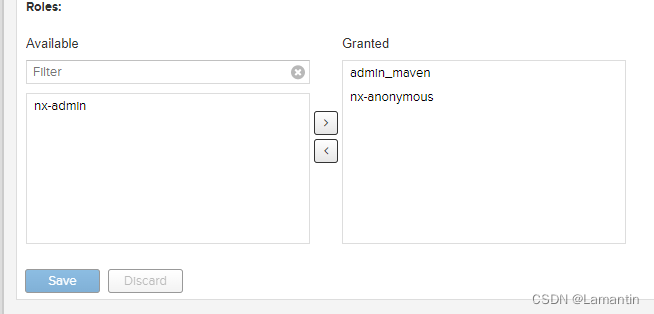
Ubuntu搭建maven私服
1.安装JDK8 已经是JDK8的需要配置环境变量,如果是更高版本的JDK则需要修改nexus配置文件 2.下载nexus安装包 百度网盘下载:链接:https://pan.baidu.com/s/1DfKqql8tZNQXEBxAEH7UyA 提取码:hx4p安装到有磁盘的目录如下所示&…...

【JavaWeb】Servlet基础
文章目录1.Tomcat服务器安装注意事项2.编写WebApp3.BS系统角色和协议4.模拟Servlet4.1模拟sun公司4.2模拟Tomcat服务器4.3模拟WebApp开发者5.开发一个带有Servlet的WebApp5.1创建一个名为crm的项目5.2 在项目中创建一个名为WEB-INF的文件(必须)5.3在WEB-…...

pinia + pinia-plugin-persistedstate + 组合式API 写法,持久化失效问题
持久化失效卡了一天的问题安装使用就不多说了,主要是针对持久化失效的几个问题说明和解决方法首先是组合式写法,配置持久化export const useUserStore defineStore(user, () > {},{persist: true} )defineStore 第三个参数,具体可以看 p…...

ptrace 调式详解
在程序出现bug的时候,最好的解决办法就是通过 GDB 调试程序,然后找到程序出现问题的地方。比如程序出现 段错误(内存地址不合法)时,就可以通过 GDB 找到程序哪里访问了不合法的内存地址而导致的。本文不是介绍GDB不是使…...
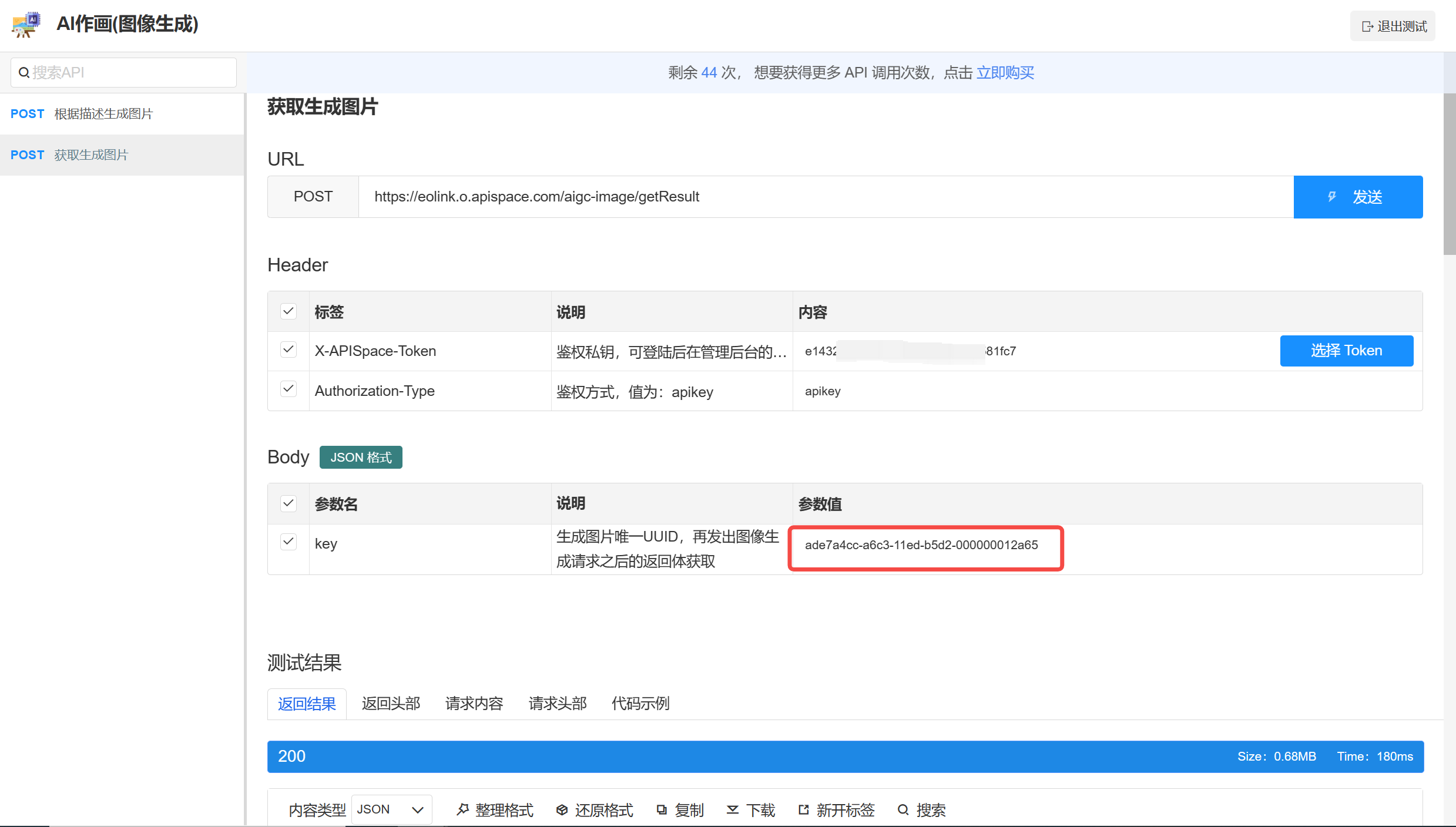
【AI绘画】绝美春天插画,人人都是插画师
春天,自然界重新苏醒,生机勃勃,百花争艳,万籁俱寂。一切都被新的生命活力所染上。春风拂面,一股清新的空气流过,仿佛带着一种神秘的力量,让人心旷神怡,心情舒畅、轻松愉悦。 突然&a…...
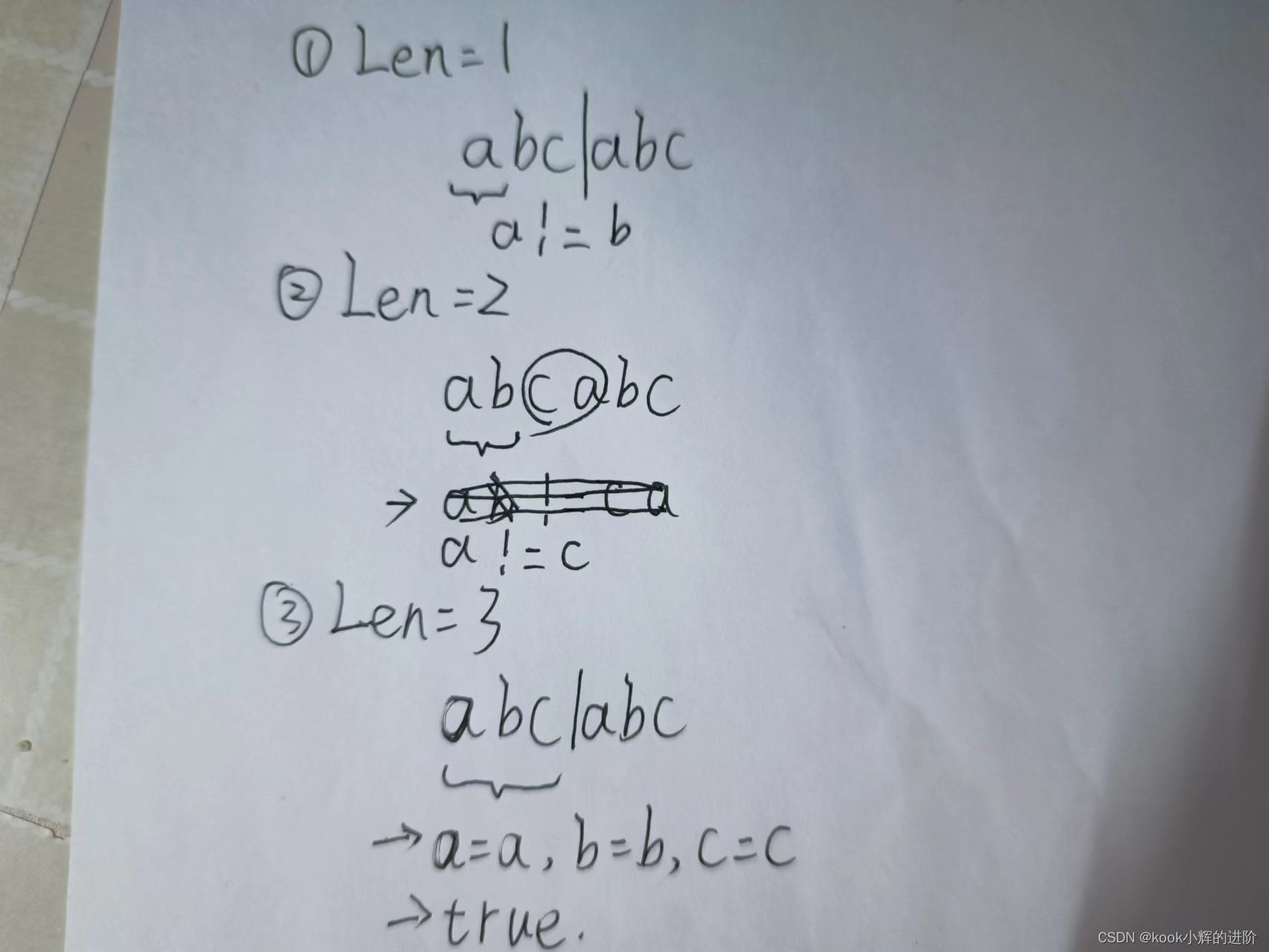
蓝桥杯入门即劝退(二十四)重复的子字符串(被秒杀)
欢迎关注点赞评论,共同学习,共同进步! ------持续更新蓝桥杯入门系列算法实例-------- 如果你也喜欢Java和算法,欢迎订阅专栏共同学习交流! 你的点赞、关注、评论、是我创作的动力! -------希望我的文章…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...