C/C++每日一练(20230301)

目录
1. 冒泡排序法排序 ★
2. 有效的数独 ★★
3. 不同的二叉搜索树 II ★★
附录
二叉搜索树
1. 冒泡排序法排序
输入n(1≤n≤10)个整数,用冒泡排序法对其从小到大排序,共进行n-1趟,要求输出每一趟的排序情况
输入格式:
先输入个数n,再输入n个整数。
输出格式:
第1趟结果
第2趟结果
......
第n-1趟结果
每个数后面有一个空格,每个序列占一行。
输入样例:
5
4 2 3 2 1输出样例:
2 3 2 1 4
2 2 1 3 4
2 1 2 3 4
1 2 2 3 4代码:
#include "stdio.h"int main()
{int arr[10];int n;scanf("%d", &n);for (int i = 0; i < n; i++)scanf("%d", &arr[i]);for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){int t = arr[j];arr[j] = arr[j + 1];arr[j + 1] = t;}}for (int j = 0; j < n; j++)printf("%d ", arr[j]);printf("\n");}return 0;
}输入输出:
5
4 2 3 2 1
2 3 2 1 4
2 2 1 3 4
2 1 2 3 4
1 2 2 3 4
--------------------------------
Process exited after 12.95 seconds with return value 0
请按任意键继续. . .
2. 有效的数独
请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
注意:
- 一个有效的数独(部分已被填充)不一定是可解的。
- 只需要根据以上规则,验证已经填入的数字是否有效即可。
示例 1:

输入:board = [["5","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出:true
示例 2:
输入:board = [["8","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出:false 解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
提示:
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'
代码:
#include <bits/stdc++.h>
using namespace std;class Solution
{
public:bool isValidSudoku(vector<vector<char>> &board){for (int i = 0; i < board.size(); i++){vector<bool> mark(10);for (int j = 0; j < board.size(); j++){if (!valid(board, mark, i, j)){return false;}}}for (int j = 0; j < board.size(); j++){vector<bool> mark(10);for (int i = 0; i < board.size(); i++){if (!valid(board, mark, i, j)){return false;}}}for (int k = 0; k < board.size(); k++){int sr = k / 3 * 3;int sc = (k % 3) * 3;vector<bool> mark(10);for (int i = sr; i < sr + 3; i++){for (int j = sc; j < sc + 3; j++){if (!valid(board, mark, i, j)){return false;}}}}return true;}
private:bool valid(vector<vector<char>> &board, vector<bool> &mark, int i, int j){if (board[i][j] != '.'){int index = board[i][j] - '0';if (mark[index]){return false;}else{mark[index] = 1;}}return true;}
};int main()
{Solution s;vector<vector<char>> board = {{'5','3','.','.','7','.','.','.','.'},{'6','.','.','1','9','5','.','.','.'},{'.','9','8','.','.','.','.','6','.'},{'8','.','.','.','6','.','.','.','3'},{'4','.','.','8','.','3','.','.','1'},{'7','.','.','.','2','.','.','.','6'},{'.','6','.','.','.','.','2','8','.'},{'.','.','.','4','1','9','.','.','5'},{'.','.','.','.','8','.','.','7','9'}};cout << s.isValidSudoku(board) << endl;board = {{'8','3','.','.','7','.','.','.','.'},{'6','.','.','1','9','5','.','.','.'},{'.','9','8','.','.','.','.','6','.'},{'8','.','.','.','6','.','.','.','3'},{'4','.','.','8','.','3','.','.','1'},{'7','.','.','.','2','.','.','.','6'},{'.','6','.','.','.','.','2','8','.'},{'.','.','.','4','1','9','.','.','5'},{'.','.','.','.','8','.','.','7','9'}};cout << s.isValidSudoku(board) << endl;return 0;
} 输出:
1
0
3. 不同的二叉搜索树 II
给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。
示例 1:
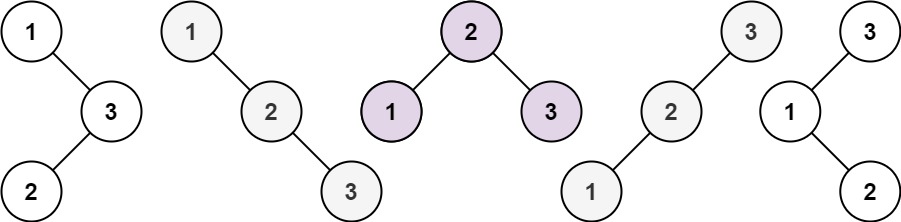
输入:n = 3 输出:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 8
代码:
#include <stdio.h>
#include <stdlib.h>struct TreeNode
{int val;struct TreeNode *left;struct TreeNode *right;
};static struct TreeNode *dfs(int low, int high, int *count)
{int i, j, k;if (low > high){*count = 0;return NULL;}else if (low == high){struct TreeNode *node = malloc(sizeof(*node));node->val = low;node->left = NULL;node->right = NULL;*count = 1;return node;}else{*count = 0;int capacity = 5;struct TreeNode *roots = malloc(capacity * sizeof(struct TreeNode));for (i = low; i <= high; i++){int left_cnt, right_cnt;struct TreeNode *left_subs = dfs(low, i - 1, &left_cnt);struct TreeNode *right_subs = dfs(i + 1, high, &right_cnt);if (left_cnt == 0)left_cnt = 1;if (right_cnt == 0)right_cnt = 1;if (*count + (left_cnt * right_cnt) >= capacity){capacity *= 2;capacity += left_cnt * right_cnt;roots = realloc(roots, capacity * sizeof(struct TreeNode));}for (j = 0; j < left_cnt; j++){for (k = 0; k < right_cnt; k++){roots[*count].val = i;roots[*count].left = left_subs == NULL ? NULL : &left_subs[j];roots[*count].right = right_subs == NULL ? NULL : &right_subs[k];(*count)++;}}}return roots;}
}static struct TreeNode **generateTrees(int n, int *returnSize)
{int i, count = 0;struct TreeNode *roots = dfs(1, n, &count);struct TreeNode **results = malloc(count * sizeof(struct TreeNode *));for (i = 0; i < count; i++){results[i] = &roots[i];}*returnSize = count;return results;
}static void dump(struct TreeNode *node)
{printf("%d ", node->val);if (node->left != NULL){dump(node->left);}else{printf("# ");}if (node->right != NULL){dump(node->right);}else{printf("# ");}
}int main(int argc, char **argv)
{if (argc != 2){fprintf(stderr, "Usage: ./test n\n");exit(-1);}int i, count = 0;struct TreeNode **results = generateTrees(atoi(argv[1]), &count);for (i = 0; i < count; i++){dump(results[i]);printf("\n");}return 0;
}
附录
二叉搜索树
又称二叉查找树或二叉排序树,BST,Binary Search Tree。一棵二叉搜索树是以二叉树来组织的,可以使用一个链表数据结构来表示,其中每一个结点就是一个对象。一般地,除了key和位置数据之外,每个结点还包含属性lchild、rchild和parent,分别指向结点的左孩子、右孩子和双亲(父结点)。如果某个孩子结点或父结点不存在,则相应属性的值为空(NULL)。根结点是树中唯一父指针为NULL的结点,而叶子结点的孩子结点指针也为NULL。
二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势;例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。
二叉搜索树能够高效地进行操作:1.插入一个数值;2.查询是否包含某个数值;3.删除某个数值。
性质
设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点,那么y.key≤x.key。如果y是x右子树中的一个结点,那么y.key≥x.key。
在二叉搜索树中:
1.若任意结点的左子树不空,则左子树上所有结点的值均不大于它的根结点的值。
2. 若任意结点的右子树不空,则右子树上所有结点的值均不小于它的根结点的值。
3.任意结点的左、右子树也分别为二叉搜索树。
复杂度
不论哪一种操作,所花的时间都和树的高度成正比。因此,如果共有n个元素,那么平均每次操作需要O(logn)的时间。
算法实现
二叉排序树的操作主要有:
1.查找:递归查找是否存在key。
2.插入:原树中不存在key,插入key返回true,否则返回false。
3.构造:循环的插入操作。
4.删除:
(1)叶子节点:直接删除,不影响原树。
(2)仅仅有左或右子树的节点:节点删除后,将它的左子树或右子树整个移动到删除节点的位置就可以,子承父业。
(3)既有左又有右子树的节点:找到须要删除的节点p的直接前驱或者直接后继s,用s来替换节点p,然后再删除节点s。
相关文章:

C/C++每日一练(20230301)
目录 1. 冒泡排序法排序 ★ 2. 有效的数独 ★★ 3. 不同的二叉搜索树 II ★★ 附录 二叉搜索树 1. 冒泡排序法排序 输入n(1≤n≤10)个整数,用冒泡排序法对其从小到大排序,共进行n-1趟,要求输出每一趟的排序情…...
Vue项目中components组件的使用笔记
目录 前言 一、components和component的区别? 二、components使用的步骤 1.创建组件vue文件 2.引入组件 3.注册组件 4.应用组件 总结 前言 本文章,只是初步了解记录components的使用步骤。 一、components和component的区别? compo…...

2023软件测试行情不行了?
一、2023年软件测试行业的现状 2020年开年,一不小心,【新冠】黑天鹅从头上飘过,持续影响全国乃至全球的经济,软件行业公司也迎来了不少的冲击,那么一个值得打算入行软件测试行业,或者已经在软件测试行业耕耘…...
【java web篇】数据库连接池Driud的使用
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...
无损音乐格式:FLAC和ALAC
前言:我最近在弄苹果的airplay项目,发现airplay2对比airplay多了音质方面的增强。AAC和MP3接触过,但对FLAC和ALAC完全不了解,整理学习资料汇总成如下信息: AirPlay2 在2017年推出,在前一代AirPlay的基础上…...
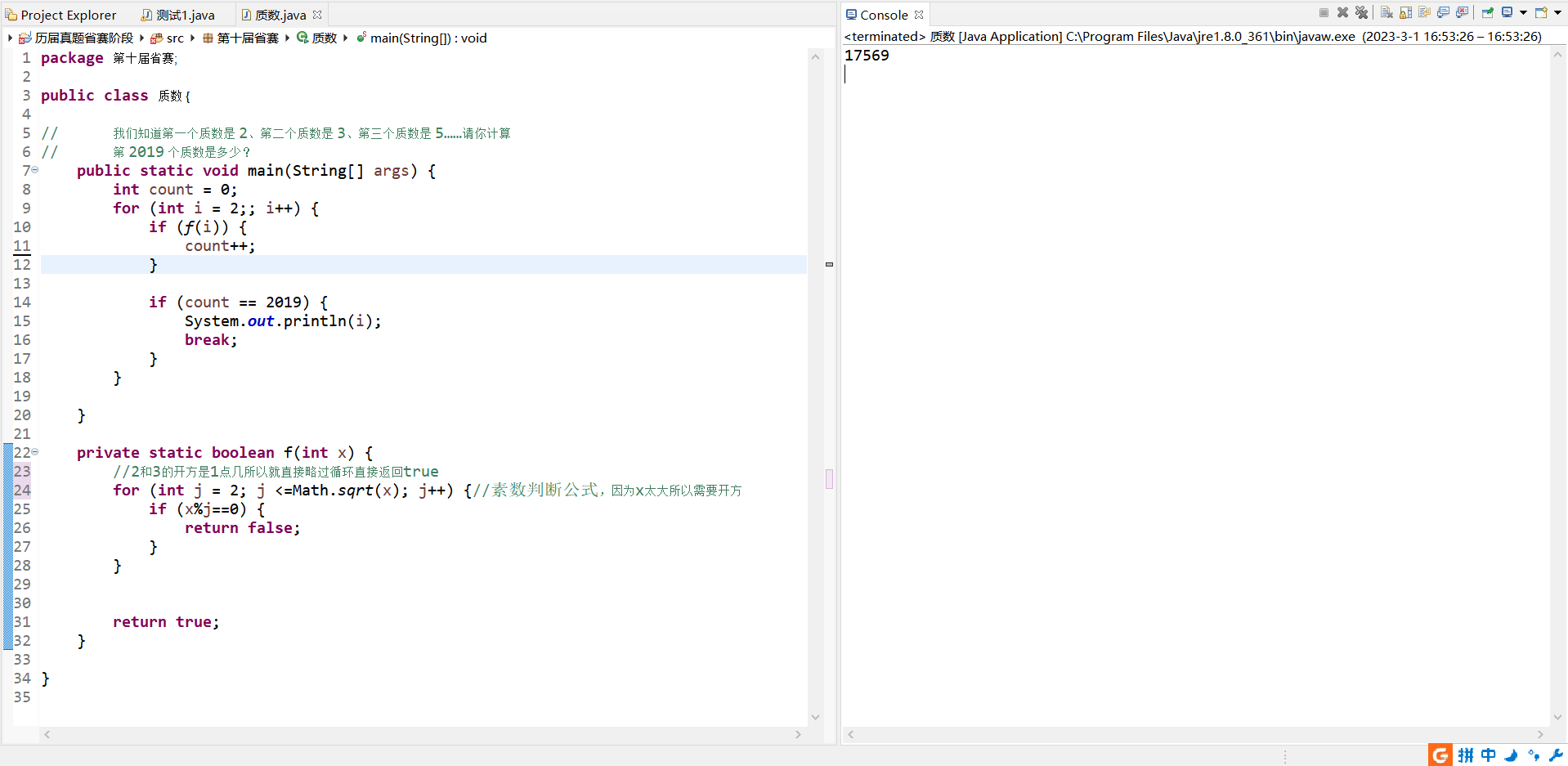
第十届蓝桥杯省赛——4质数(质数判断,数学函数:开方函数)
题目:试题 D: 质数本题总分:10 分【问题描述】我们知道第一个质数是 2、第二个质数是 3、第三个质数是 5……请你计算第 2019 个质数是多少?【答案提交】这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数&…...

MASKGROUP: HIERARCHICAL POINT GROUPING AND MASKING FOR 3D INSTANCE SEGMENTATION
ABSTRACT 本文研究了 3D 实例分割问题,该问题在机器人技术和增强现实等现实世界中具有多种应用。由于3D物体的周围环境非常复杂,不同物体的分离非常困难。为了解决这个具有挑战性的问题,我们提出了一个新的框架来对 3D 实例进行分组和优化。在实践中,我们首先为每个点学习…...
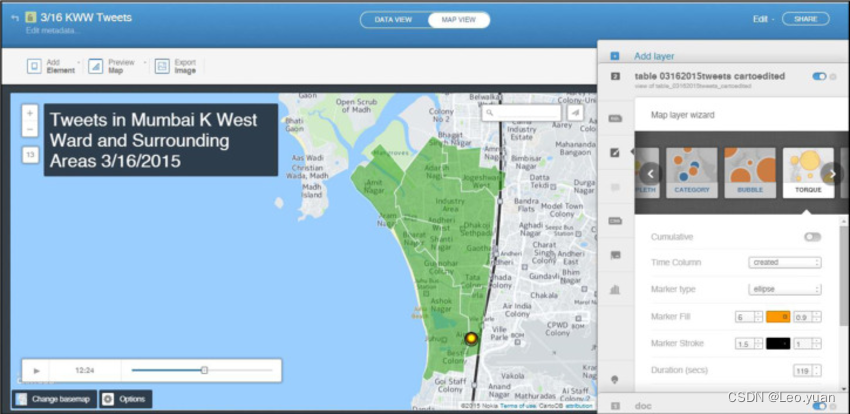
为什么地图可视化炙手可热?
我们在谈到数据可视化的时候,可能第一反应就是中间有一个地图样式的大屏图。但有没有想过,为什么大多数的可视化大屏中间都是一张地图的样子?这张地图样式的模块究竟是什么呢?它又是怎么做出来的? 其实这张地图样式的…...

JAVA代码审计篇-SQL注入
JAVA代码审计篇-SQL注入1、SQL注入漏洞简介2、SQL注入的条件3、审计方法4、JAVA中执行SQL的几种方式(1)使用JDBC的java.sql.Statement执行SQL语句(2)使用JDBC的java.sql.PreparedStatement执行SQL语句(3)使…...

SpringBoot接口传参方式
常见GET请求和POST请求的区别1.get请求无消息体,只能携带少量数据,且不安全post请求有消息体,可以携带大量数据,且安全2.携带数据的方式:get请求将数据放在url地址中post请求将数据放在消息体body中传参方式get方式---…...
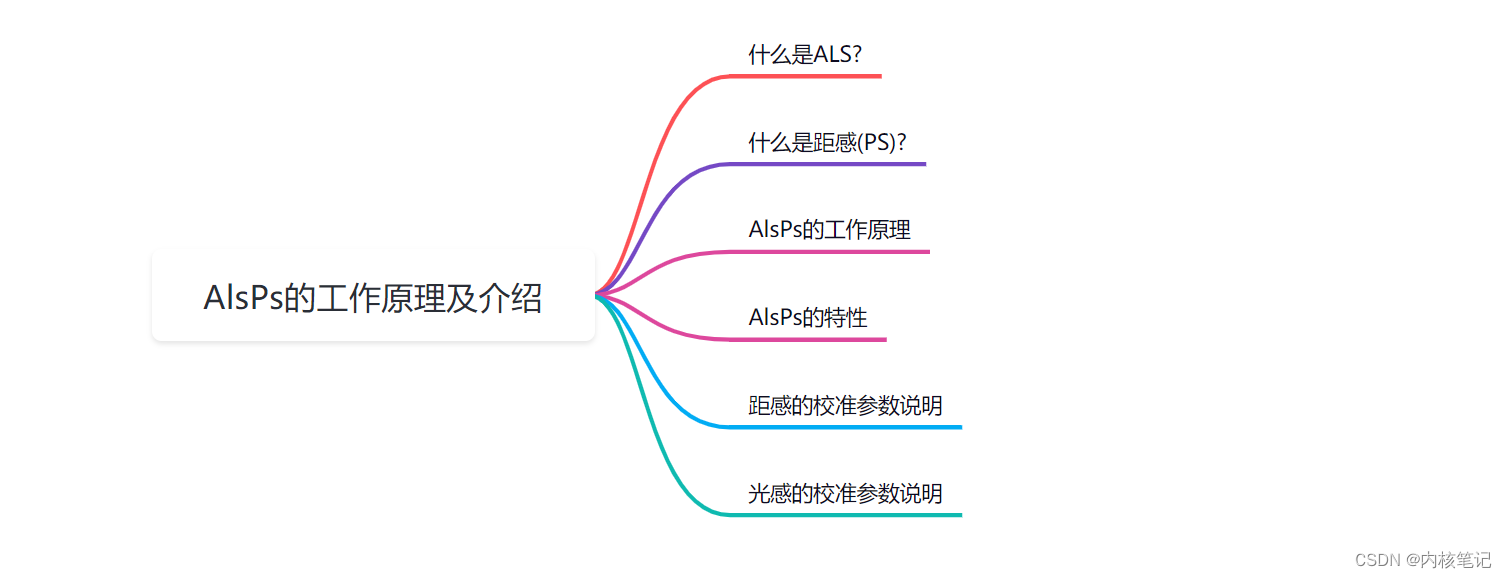
高通平台开发系列讲解(Sensor篇)AlsPs的工作原理及介绍
文章目录 一、什么是ALS?二、什么是距感(PS)?三、AlsPs的工作原理四、AlsPs的特性五、距感的校准参数说明六、光感的校准参数说明沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇文章将介绍 AlsPs 的工作原理及介绍。 一、什么是ALS? 光感的英文叫做Ambient Li…...

集群方式下的java Redis锁 lua脚本
下面说一下集群方式redis 下的原子锁 带超时时间java 代码如下:List<String> keys Collections.singletonList("test_key1");System.out.println("打印前 ::"jedisCluster.get("test_key1"));//获取lua …...

【钓鱼实测】写bug给new bing和chatGPT查。问他们林黛玉倒拔垂杨柳
BUG 错误代码 #include <iostream> #include <vector> using namespace std; int main() {vector<int> vec{1,2,3,2,4};for (auto iter vec.begin(); iter ! vec.end(); iter ){if (*iter 2) {vec.erase(iter);}}cout << vec.size() << endl…...

基于OMAPL138+FPGA核心板多核软件开发组件MCSDK开发入门(上)
本文测试板卡为创龙科技 SOM-TL138F 是一款基于 TI OMAP-L138(定点/浮点 DSP C674x + ARM9)+ 紫光同创 Logos/Xilinx Spartan-6 低功耗 FPGA 处理器设计的工业级核心板。核心板内部OMAP-L138 与 Logos/Spartan-6 通过 uPP、EMIFA、I2C 通信总线连接,并通过工业级 B2B连接器引…...

C#/.net程序调用python
C#/.net程序调用python C#的优势在于window下的开发,不仅功能强大而且开发周期短。而python则有众多的第三方库,可以避免自己造轮子,利用C#来做界面,而具体实现使用python来实现可以大大提高开发效率。本文介绍如何使用pythonnet…...
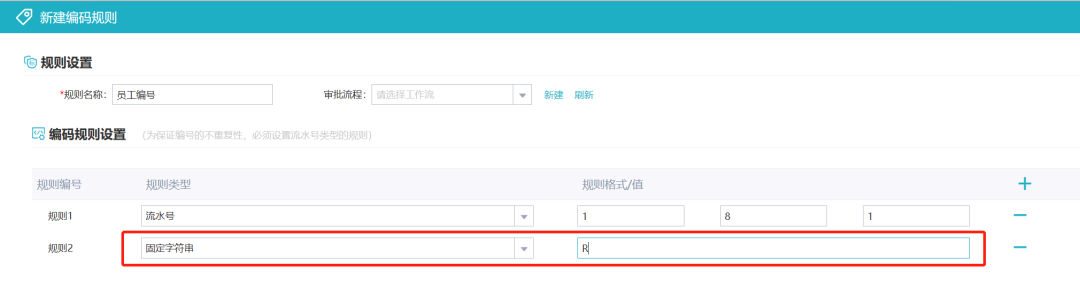
一文讲清楚如何进行主数据编码
主数据编码作为一类重要的数据资源,在信息化建设中具有重要的地位和作用,是保证现有信息系统和未来新系统建设成功的关键因素,决定着系统中的信息一致性。 编码,是一件简单的事情,但绝对不是一件容易做好的事情&#…...
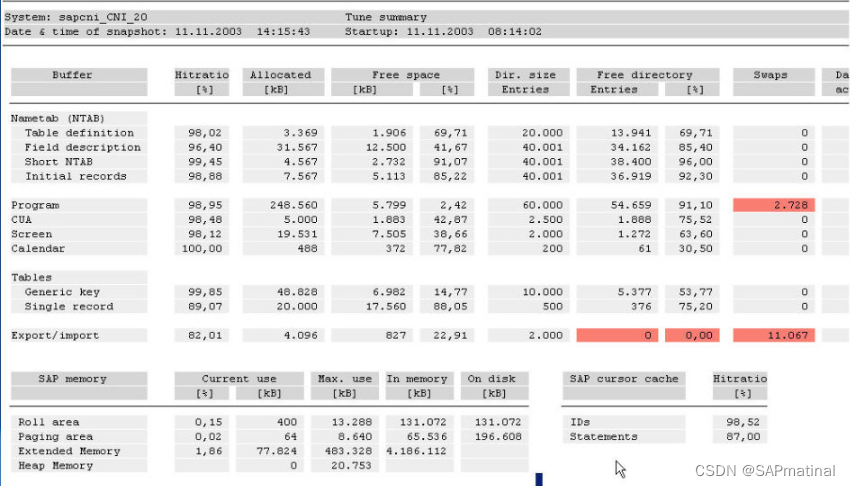
SAP 详解ST02
问:在st02中看到,Program和Export/Import的Swap出现红的了,这个是什么原因啊,是不是对系统的性能有影响啊,是否应该调整一些参数啊。要怎么调整呢? 复1:双击红色的部分就可以看到相应的参数修改…...
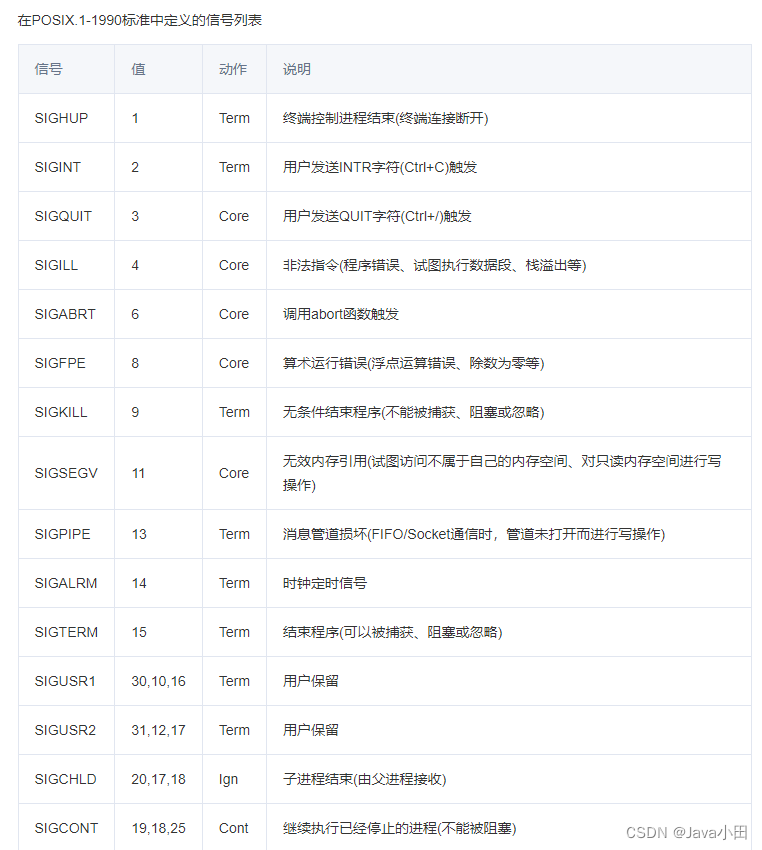
Go程序当父进程被kill,子进程也自动退出的问题记录
平常我们启动一个后台进程,会通过nouhp &的方式启动,这样可以在退出终端会话的时候,进程仍然可以继续在后台执行(进程的父进程id会从原来的bash进程变成1) 在go程序中,通过nouhp &的方式启动子进程,预期是即使…...

window10 下使用docmer-compose使用mysql镜像部署mysql
1. 在wins中找到store,安装Debian 2. 在桌面右键点击 linux shell窗口 3. 安装docker 4. 启动docker: service docker start 5. 配置加速器,为了拉取镜像更快,修改后得重新启动docker: vi /etc/docker/daemon.json…...

软件测试补充
软件开发的生命周期:需求-计划-设计-开发编码-测试-运行维护-上线 那我们的微信APP来进行举例: 需求:我需要你们团队做这样一个社交软件,能够像QQ一样实现聊天功能,发布说说的功能,能够群聊,可以转账 计划:计划软件…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
