【代码随想录训练营】【Day28】第七章|回溯算法|93.复原IP地址|78.子集|90.子集II
复原IP地址
题目详细:LeetCode.93
这道题与上一道练习题分割回文字符串十分详细,一样是涉及到分割字符串、判断字符串、递归与回溯的问题,所以这道题要解决的难点在于:
- 如何分割IP地址字符串
- 如何判断分割的IP地址是否合法
- 递归的结束条件要如何设置
首先解决“如何判断分割的IP地址是否合法”,我们要知道一个合格的IP的地址的要求,在这道题中的要求比较简单,只要满足:
- IP地址中号段可以为0,但不存在以0开头的号段
- IP地址长度为4个字节,每一个号段的长度为1个字节,即其大小空间为28 = 256,每一个号段用十进制表示的范围为0~255
其次是“如何分割IP地址字符串”,这里的分割思路于分割回文字符串非常相似:
- 在分割的过程中,对每一次分割的号段字符串都进行合法性验证
- 如果当前号段合法,在其后续插入分割符 ‘.’ ,然后进入递归,继续分割下一个号段
- 如果当前号段不合法,说明在当前位置进行分割的话,已经是一个不合法的IP地址了,所以无需继续分割,直接break跳出当前循环。
最后是“递归的结束条件要如何设置”,观察IP地址的特点可知:
- 一个IP地址最多存在3个分割符 ‘.’
那么我们就可以递归参数中设置一个变量来记录分割符的数量,如果数量==3时,即说明该IP地址分割完毕。
不过需要注意,我们在之前的分割的过程中,是先判断字段合法之后再添加分割符,所以当分割符数量==3之后,还需要对最后的号段进行合法性验证,以此来判断待添加的IP地址是否真的合法;无论是否合法都要return,因为这是递归的结束条件。
Java解法(递归,回溯):
class Solution {List<String> ans = new ArrayList<>();public boolean isVaild(String s, int begin, int end){if (begin >= end || (end - begin) > 3) {return false;}// 0开头的数字不合法if (s.charAt(begin) == '0' && begin != end - 1) { return false;}int num = 0;// 遇到非数字字符不合法for (int i = begin; i < end; i++) {if (s.charAt(i) > '9' || s.charAt(i) < '0') { return false;}num = num * 10 + (s.charAt(i) - '0');// 如果大于255了不合法if (num > 255) { return false;}}return true;}public void backtracking(StringBuffer sb, int startIndex, int pointNums){if(pointNums == 3){if(isVaild(sb.toString(), startIndex, sb.length()))ans.add(sb.toString());return;}for(int i = startIndex; i < sb.length(); i++){if(isVaild(sb.toString(), startIndex, i + 1)){sb.insert(i + 1, '.');pointNums++;backtracking(sb, i + 2, pointNums);sb.deleteCharAt(i + 1);pointNums--;}else continue;}}public List<String> restoreIpAddresses(String s) {if(!(s.length() > 12 || s.length() < 4)){backtracking(new StringBuffer(s), 0, 0);}return this.ans;}
}
子集
题目详细:LeetCode.78
经过前面那些一知半解的练习之后,到了这道题,我终于领悟到了如何去打开回溯的解题思路,当遇到回溯问题时,我们立刻将问题转化都树形结构,开始画图(必须画图来理解,除非你空间想象力真的很好,我一开始凭空想了很久,但很容易乱,决定画图之后,发现一切都十分明辽了):

画得非常草稿化,从前面回溯的理论基础和回溯解题模版可知:
- 回溯问题其实就是一个收集树形结构节点结果或路径结果的问题
- 循环的次数决定了树的宽度,相当于对树进行同层访问
- 递归的层数,就是循环的嵌套层数,相当于对树进行深度访问
- 递归的结束条件,就是回溯的条件,相当于访问到树的叶子节点
回到这道题,我们将问题转换为树形结构后,对应的就可以发现:
- 一个数字也可以是一个子集,所以在每次循环中,只取一个数字,可以定一个变量 start 来标识当前应该取哪个下标的数字
- 要求不能包含重复的子集,所以在进入递归时,要将当前的数字包括其之前的数字都分割出去,这里我们利用下标变量 start 来控制从数字开始访问
- 每访问一个节点,其路径上的节点集合,就是一个结果,所以要在循环和遍历过程中就将结果加入结果集
- 当nums数组为空时,即下标到达数组边界 start == nums.length 时,就是递归的结束条件,即回溯的条件
Java解法(递归,回溯):
class Solution {List<List<Integer>> ans = new ArrayList<>();Deque<Integer> path = new ArrayDeque<>();public void backTrack(int[] nums, int start){if(nums.length == start){return;}for(int i = start; i < nums.length; i++){path.offer(nums[i]);ans.add(new ArrayList<Integer>(path));backTrack(nums, i + 1);path.removeLast();}}public List<List<Integer>> subsets(int[] nums) {ans.add(new ArrayList<Integer>());this.backTrack(nums, 0);return this.ans;}
}
子集II
题目详细:LeetCode.90
这道题与上一题的区别在于:整数数组nums可能包含重复的元素,依旧是要求返回不重复的子集集合。
那么其实就是在上一题的基础上,在树形结构上进行剪枝,达到在循环和递归过程中进行去重的目的,这样类似的题目在之前也有做过:【Day27】第七章|回溯算法|39. 组合总和|40.组合总和II
是首先画图辅助理解:

通过之前的练习,我知道在递归结束时再进行去重操作中,在这一题同样会出现超出时间限制的情况,所以在这里就不重蹈覆辙了,所以难点就时如何在循环和递归的过程中,就对结果进行去重。
通过画图我们可以发现,去重操作或者说如何去判断是否会出现重复的结果,都是在树的同一层中进行处理的:
- 在循环过程中,当我们依次访问数组中的元素时,如果前一个元素与当前元素相等,那么我们再对当前元素进行递归操作的话,就有可能出现与前一个元素同样的子集
- 为什么说是有可能呢,而不是一定呢,因为可能还存在着如图中 [1, 2, 2] 这样带有重复元素的子集,所以为了避免丢失了部分子集,
我们需要提前对数组进行排序,使其相同大小的数字都是连续的 - 同时也说明了去重操作需要在树的宽度访问中进行,而不是在树的深度访问中进行,也就是在进入递归前就进行去重判断
- 在这一道题中,我们可以利用一个布尔数组used来辅助去重
- 当
nums[i] == nums[i - 1] && used[i] == true时,说明虽然前一个数字已被访问,但是还未被回溯,进一步说明在树形结构中,当前路径还未到达叶子节点,在路径上还可能存在其他子集结果,需要继续递归到下一层 - 当
nums[i] == nums[i - 1] && used[i] == false时,说明虽然前一个数字与当前数字相同,但是由于递归是深度优先遍历,所以前一个数字之所以是used[i - 1] == false,是因为它已经被回溯了,其所有路径上的子集都已添加进结果集,如果再对当前数字继续递归的话,则会出现与前一个数字重复的子集,所以不需要在对当前数字进行递归,直接进入下一层循环
- 当
Java解法(递归,回溯,哈希):
class Solution {List<List<Integer>> ans = new ArrayList<>();Deque<Integer> path = new ArrayDeque<>();public void backTrack(int[] nums, boolean[] used, int startIndex){if(nums.length == startIndex){return;}for(int i = startIndex; i < nums.length; i++){if(i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){continue;}path.offer(nums[i]);used[i] = !used[i];ans.add(new ArrayList<Integer>(path));backTrack(nums, used, i + 1);path.removeLast();used[i] = !used[i];}}public List<List<Integer>> subsetsWithDup(int[] nums) {boolean[] used = new boolean[nums.length];Arrays.sort(nums);this.ans.add(new ArrayList<Integer>());this.backTrack(nums, used, 0);return this.ans;}
}
第一次接触到回溯,这两天做题总是停留在一知半解的地步,懵懵懂懂的,本来想要囫囵吞枣,得过且过算了,没想到最后两道练习题我突然醒悟,遇见回溯题就应该先将其转换为树形结构,通过画图来辅助理解整个循环、递归与回溯的过程,这入门的过程是如此的艰难,但是思路打开之后,一切都变得那么的通透了,真叫人:
初极狭,才通人,步行数十步,豁然开朗。
相关文章:

【代码随想录训练营】【Day28】第七章|回溯算法|93.复原IP地址|78.子集|90.子集II
复原IP地址 题目详细:LeetCode.93 这道题与上一道练习题分割回文字符串十分详细,一样是涉及到分割字符串、判断字符串、递归与回溯的问题,所以这道题要解决的难点在于: 如何分割IP地址字符串如何判断分割的IP地址是否合法递归的…...

Get请求和Post请求区别
前后端交互请求数据的方式有很多种。 例如:Get Post Put Patch Delete Copy 等等很多请求方式 但是用的最多的就是Get和Post Get请求方式 1. get多用于从服务器请求获取数据 2.get传送的数据量较小,不能大于2KB 3.get安全性非常低 Post请求方式 1.…...

static关键字
static的基本基本用法可以分为下面几种: (1)static修饰全局变量 (2) 修饰局部变量 (3)修饰普通函数 (4)修饰类的成员变量 一、static修饰全局变量 当同时编译多个文件时…...

A Comprehensive Tool for Modeling CMOS Image-Sensor-Noise Performance论文总结及翻译
A Comprehensive Tool for Modeling CMOS Image-Sensor-Noise Performance Author: Ryan D. Gow Link: https://ieeexplore.ieee.org/document/4215175/metrics#metrics Select: ⭐️⭐️⭐️⭐️ Type: Academic Journal 备注: CMOS图像传感器噪声性能建模的综合工具 总结 …...

嘀嗒出行再闯IPO:千军万马我无懈
羽扇纶巾笑谈间,千军万马我无懈。 在激烈竞争中再度冲刺港交所IPO的嘀嗒出行,闪露出一丝歌词里的气魄。交通运输部下属网约车监管信息交互系统的数据显示,截至2023年1月31日,全国共有300家网约车平台公司取得网约车平台经营许可。…...
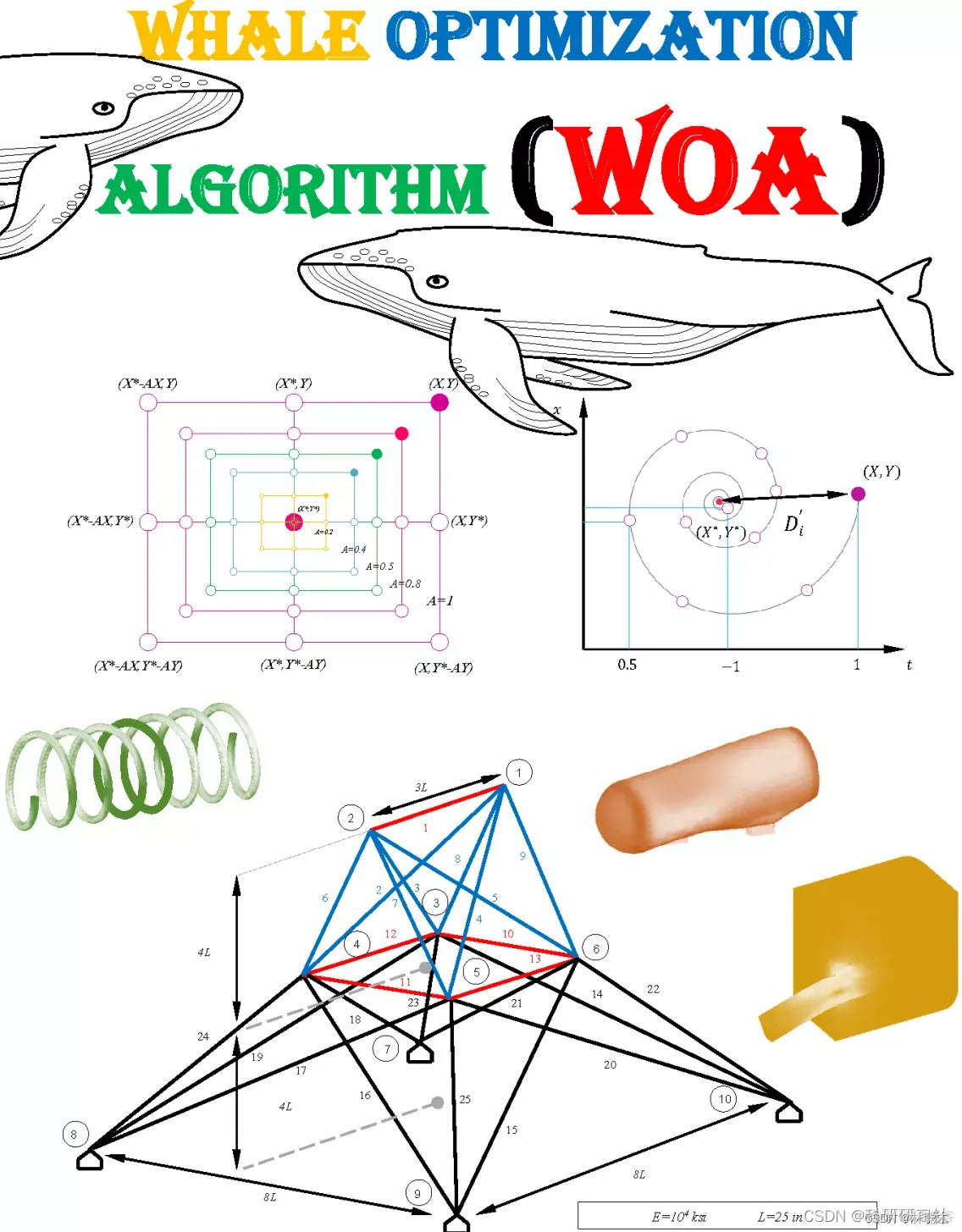
MATLAB算法实战应用案例精讲-【优化算法】增强型鲸鱼优化算法(EWOA)(附matlab代码实现)
前言 增强型鲸鱼优化算法(Enhanced Whale Optimization Algorithm,EWOA)是Mohammad H. Nadimi-Shahraki等人于2022年提出的一种改进算法。由于标准的鲸鱼优化算法及其它的改进算法都存在种群多样性低和搜索策略差的问题,因此引入有效的策略来缓解鲸鱼优化算法的这些核心缺点…...
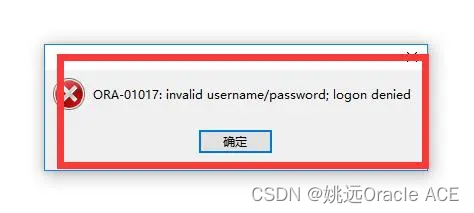
登录Oracle数据库遇到ORA-01017密码错误的解决办法
文章目录症状分析解决办法欢迎加下方我的微信👇,拉你入学习群我们在登录Oracle数据库时可能会遇到ORA-01017错误,这里分析原因并提供解决办法。点击试看博主的专著《MySQL 8.0运维与优化》(清华大学出版社) 症状 图像…...
10个黑客基础教程!简单有效
如果你的电脑运行缓慢,请使用下面介绍的方法来帮助加速、优化和提高电脑的性能。 1.关闭启动时自动运行的应用程序 计算机上安装的许多应用程序都可以将自己配置为在启动期间自动启动并继续在后台运行,但是,如果不是每天都使用这些应用程序…...

JPA之实体之间的关系
JPA之实体之间的关系 10.1.1实体类创建 注解的应用 Table,Entity IdGeneratedValue指定主键,Column P174 实体类编写规范 Table(name "t_user") Entity(name "User") public class User implements Serializable {IdGeneratedVa…...
?)
如何在 C++ 中调用 python 解析器来执行 python 代码(三)?
本文在 C 中调用 multi.py 脚本,并向它传入参数并执行,然后获得返回值并在 C 中打印结果。 目录 如何在 C 中调用 python 解析器来执行 python 代码(一)?如何在 C 中调用 python 解析器来执行 python 代码࿰…...

【Linux】gcc/g++/gdb的使用
🔥🔥 欢迎来到小林的博客!! 🛰️博客主页:✈️小林爱敲代码 🛰️社区 : 进步学堂 🛰️欢迎关注:👍点赞🙌收…...
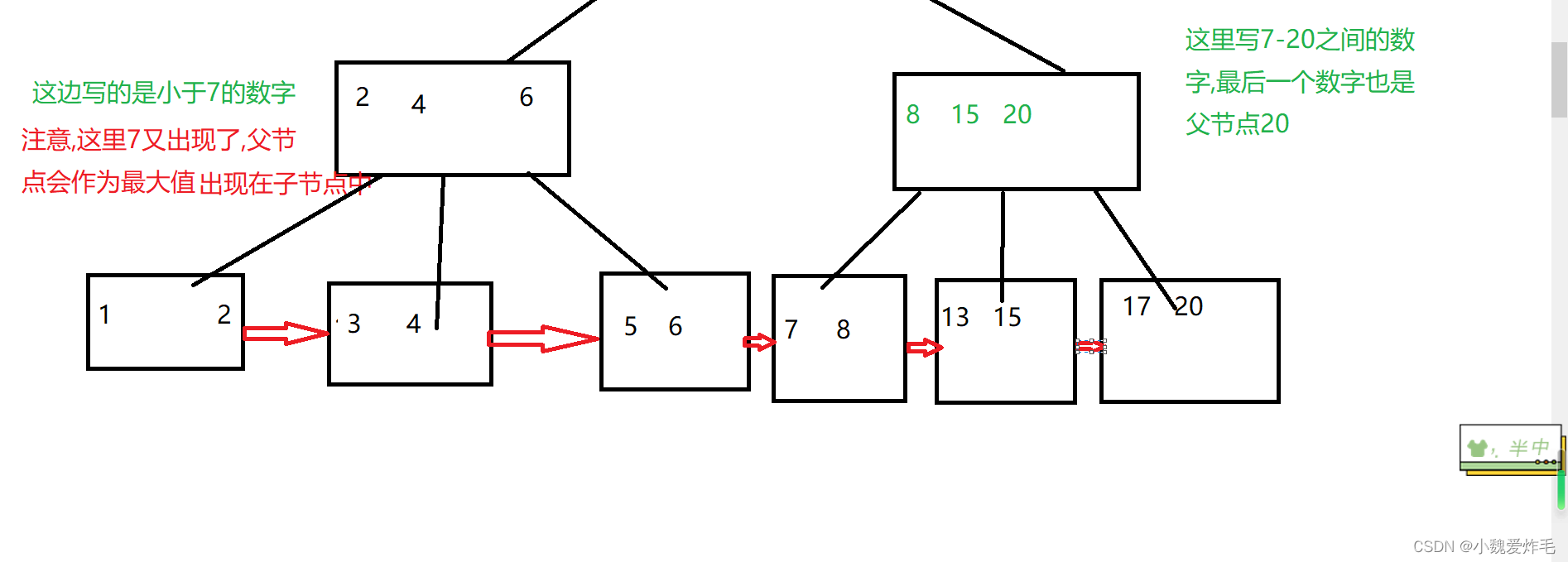
浅浅谈一谈B树和B+树
目录: 🚀1.B树 🚀2.B树 索引背后的数据结构是啥呢,是B树,是为了数据库索引设计的,我们可以先了解B树,再说B树 1.什么是B树 B树也叫B-树,这里的-不读减,是一个符号 我们已经学过了二叉搜素树,B树其实就是N叉搜素树,二叉搜索树只能在每一个结点放一个…...
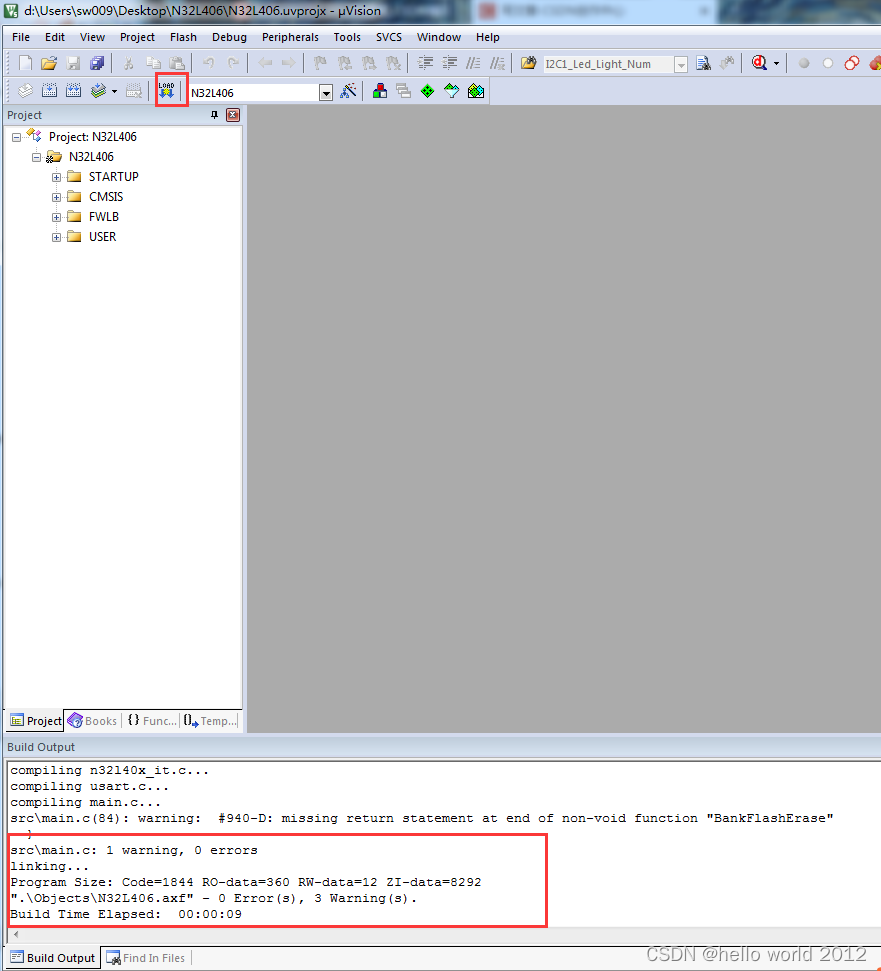
Keil新建一个国民32位MCU工程
1.打开Keil软件,点击Project→New uVision→Project 2.将工程保存到自己的工程文件夹,并给项目命名,点击保存 3.选择自己需要开发的芯片,点击OK 4.点击OK 5.出现上图所示,工程已经建好了,点击配置工程。 6.…...

webpack.config.js与package.json文件的配置
path要使用绝对路径,通过每次复制文件位置非常麻烦且容易导致问题 使用node中的 写个包名跟入口名称,其他全部回车 此步完成后,自动生成一个package.json包 licence指的是开源,一般不写 安装文件夹需要的依赖 dirname是node自带…...
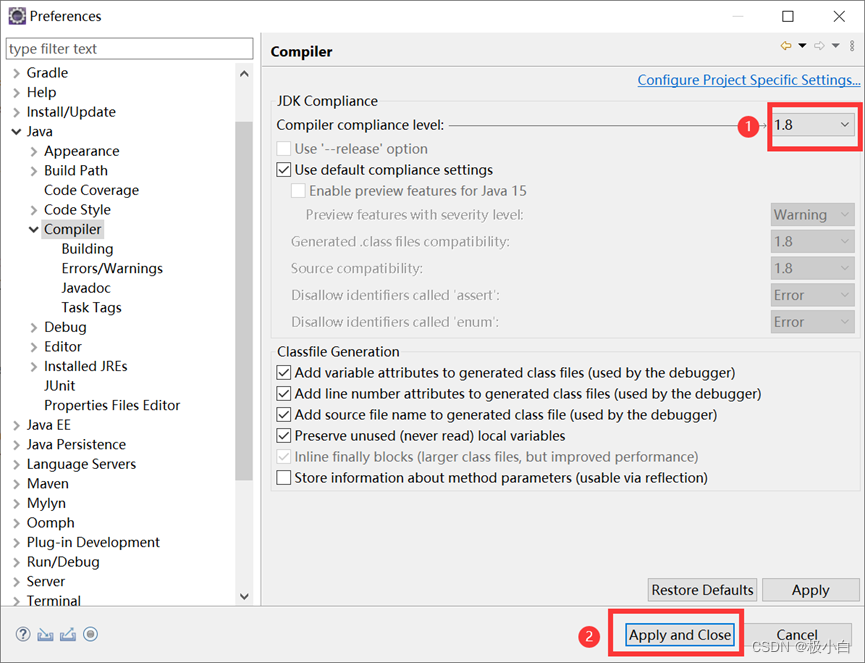
超详细Eclipse配置JDK
在此附上Eclipse安装教程 超详细Eclipse安装教程 在此附上JDK1.8安装配置教程 超详细JDK1.8安装与配置 ①打开Eclipse–>点击Window–>点击Preferences ②找到Java–>找到Installed JREs–>点击Add… ③选中Standard VM–>之后点击Next ④点击Directory找…...

成功解决numpy.linalg.LinAlgError: SVD did not converge in Linear Least Squares
成功解决numpy.linalg.LinAlgError: SVD did not converge in Linear Least Squares 目录 解决问题 解决思路 解决方法—四大原因分析 T1、数据本身问题的解决方法...
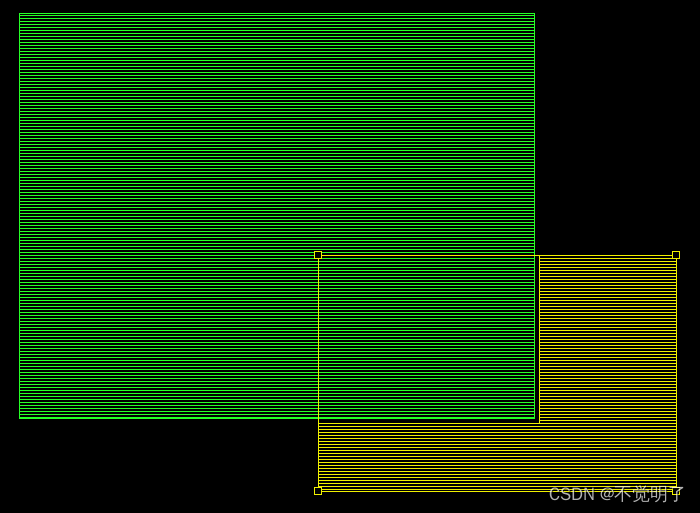
Allegro如何设置铜皮避让的优先级操作指导
Allegro如何设置铜皮避让的优先级操作指导 在用Allegro进行PCB设计的时候,时常需要使用动态铜皮进行设计,当两块动态铜皮存在交集的时候,避让就会存在一个优先级,如下图 上方的铜皮避让调了下方的铜皮,上方的铜皮被避让了 如何调整让下方的铜皮避让上方的铜皮,如下图 具…...

(Trie Tree)字典树
(Trie Tree)字典树 场景:在n个字符串中查找某个字符串。 暴力匹配,时间复杂度为O(nm),m为字符串平均长度,效率过低。 字典查找单词"fly",首先查找’f’,然后…...

MQTT的学习之Mosquitto集群搭建
文章钢要: 1、进行双服务器搭建 2、进行多服务器搭建 一、Mosquitto的分布式集群部署 如果需要做并发量很大的时候就需要考虑做集群处理,但是我在查找资料的时候发现并不多,所以整理了一下,搭建简单的Mosquitto集群模式。 首…...

TS面向对象
第二章:面向对象 面向对象简而言之就是程序之中所有的操作都需要通过对象来完成。 举例来说: 操作浏览器要使用window对象操作网页要使用document对象操作控制台要使用console对象 一切操作都要通过对象,也就是所谓的面向对象,…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
