I - 太阳轰炸(组合数学Cnk n固定)
2023河南省赛组队训练赛(二) - Virtual Judge (vjudge.net)
背景:阿塔尼斯,达拉姆的大主教,在艾尔又一次沦陷之后指挥着星灵的最后一艘方舟舰:亚顿之矛。作为艾尔星灵数千年来的智慧结晶,亚顿之矛除了搭载了以太阳能碎片为核心的兵工厂之外,还配备了诸如汇聚射线、太阳能射线枪等威力强大的支援武器。而在这些武器中,最负盛名、也最让敌人胆寒的就是太阳轰炸。
太阳轰炸是一件威力巨大的对星球武器。在太阳轰炸开火时,亚顿之矛将聚集太阳能核心中的太阳能量,向目标坐标发射成百上千枚火焰飞弹。虽然这些火焰飞弹精准度较差,但太阳轰炸的高攻击频率仍然可以让地面上的敌人无法躲避,化为灰烬。
在这一次的行动中,阿塔尼斯的目标是一枚臭名昭著的虚空碎片。在俯视视角下,虚空碎片的投影是一个半径为 R1 的圆,太阳轰炸的攻击散布范围是一个半径为 R2 的圆。这两个圆的圆心均为原点 (0, 0)。太阳轰炸将射出 n 枚火焰飞弹,每一枚火焰飞弹等概率地落在攻击散布范围内每一个点上,所有火焰飞弹的落点相互独立。火焰飞弹的伤害范围是以落点为圆心,半径为 r 的圆。若火焰飞弹的伤害范围和虚空碎片的投影相交,则该枚火焰飞弹命中虚空碎片,造成 a 点伤害。若总伤害大于等于 h,则虚空碎片会被摧毁。
摧毁这枚虚空碎片对阿塔尼斯的战略部署非常重要,因此阿塔尼斯想要知道一次太阳轰炸能够摧毁这枚虚空碎片的概率。你需要输出答案对质数 109 + 7 取模的值。
Input
仅一行,包含六个整数 n, R1, R2, r, a, h (1 ≤ n ≤ 5 × 106, 1 ≤ R1, R2, r ≤ 108, 1 ≤ a, h ≤ 108),含义见题目描述。
Output
一个整数,表示答案。
Sample 1
| Inputcopy | Outputcopy |
|---|---|
3 2 4 1 1 1 | 636962896 |
Note
答案对质数 109 + 7 取模的定义:设 M = 109 + 7,可以证明答案可表示为一个既约分数

,其中 p, q 均为整数且 q 模 M 不余 0。输出满足 0 ≤ x < M 且 x·q ≡ p ± od{M} 的整数 x。
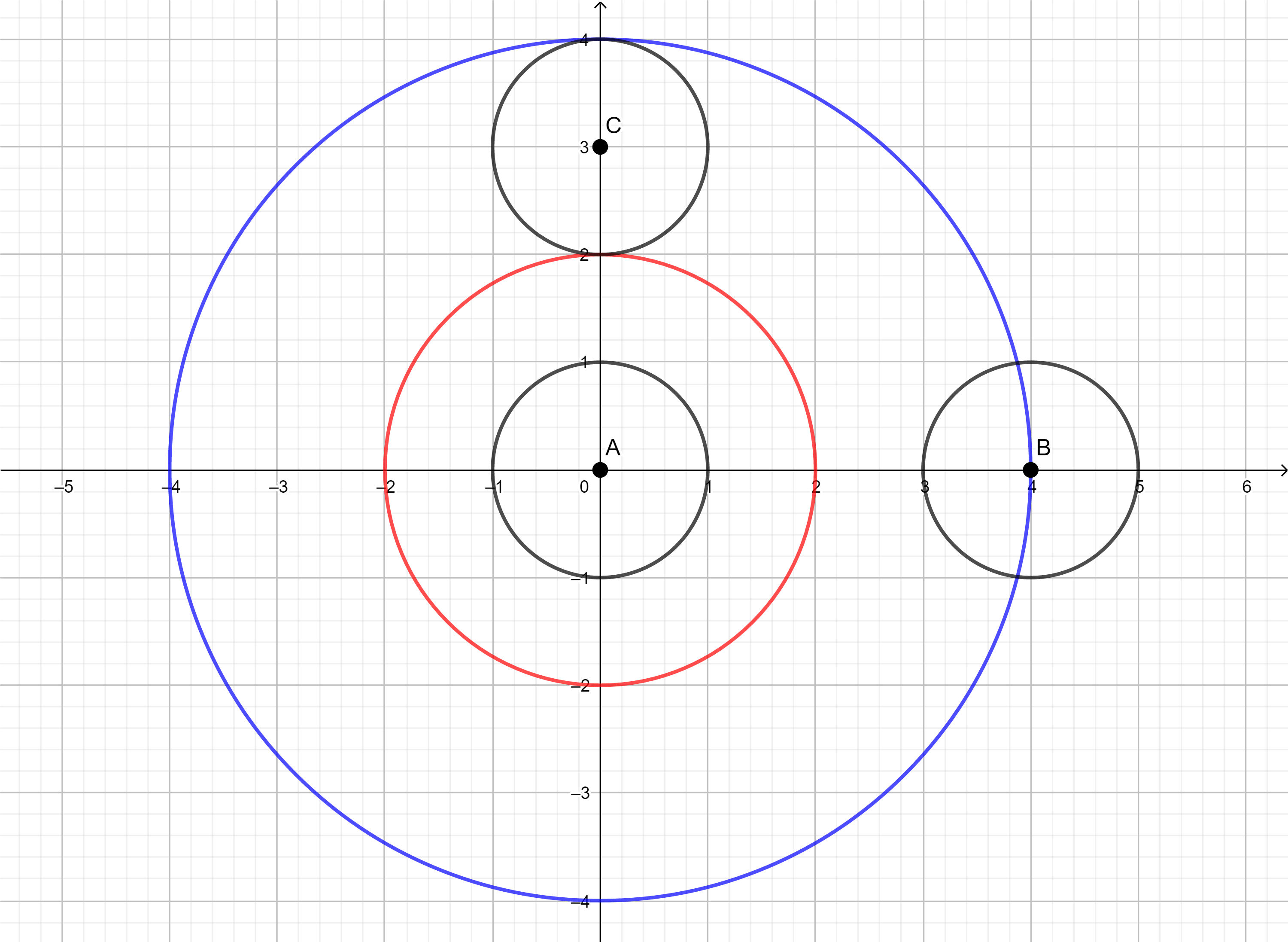
上图对应了样例中 R1 = 2, R2 = 4, r = 1 的情况。其中红色的圆是虚空碎片的投影,蓝色的圆是太阳轰炸的攻击范围。A, B, C 是三个可能的落点,其中 A, C 命中虚空碎片,而 B 没有命中虚空碎片。
题解:
1.概率为0,炮弹伤害全部命中也无法摧毁碎片
2.概率为1,炮弹的落范围R2 <= R1 + r
3.外面又一个环炮弹骗的范围
命中概率即为(R1 + r)*(R1 + r)/(R2 * R2) = p1
未命中概率即为((R1*R2) - (R1 + r)*(R1 + r))/(R2 * R2) = p2
根据组合数学命中总概率为
Cnk*(p1)^k*p2^(n-k) + Cn(k+1)*(p1)^(k+1)*p2*(n-k-1) .......
Cnn*p1^n*p2^(n-n)
本题主要难点就是线性时间如何求出每一个Cnk
我们可以1*2*3..*n得到fa[n]
然后qpow(fa[n],mod-2)得到fa[n]的逆元g[n]
fa[n-1]的逆元就是g[n]*n依次类推
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<vector>
#include<map>
#include<queue>
using namespace std;
#define int long long
const int N = 6e6 + 10;
int mod = 1e9 + 7;
#define ios ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
int fa[N];
int g[N];
int t[N];
int y[N];
int qpow(int x,int p)
{int a = 1;while(p){if(p&1)a = a*x%mod;x = x*x%mod;p /= 2;}return a;
}
int C(int n,int m)
{return fa[n]*g[m]%mod*g[n-m]%mod;
}
void solve()
{int n,r1,r2,r,a,h;cin >> n >> r1 >> r2 >> r >> a >> h;int k ;if(h%a == 0){k = h/a;}else{k = h/a + 1;}if(k > n){cout<<"0";return ;}if(r2 <= (r1 + r)){cout <<"1\n";return ;}fa[0] = g[0] = 1;int z = (r1 + r)*(r1 + r)%mod;int x = (r2*r2%mod - (r1 + r)*(r1 + r)%mod + mod)%mod;int c= r2*r2%mod; for(int i = 1;i <= n;i++){fa[i] = fa[i-1]*i%mod;}g[n] = qpow(fa[n],mod - 2);for(int i = n -1;i >= 0;i--){g[i] = g[i+1]*(i+1)%mod;}int zx = 1;for(int i = 1;i <= n;i++){zx = zx*c %mod;}t[0] = 1,y[0] = 1;for(int i = 1;i <= n;i++){t[i] = t[i - 1]*z%mod;y[i] = y[i-1]*x%mod; }int s = 0;for(int i = k;i <= n;i++){s = (s + (C(n,i) * t[i]%mod*y[n - i]%mod) %mod)%mod;}cout << s*qpow(zx,mod-2)%mod;}
signed main()
{
// ios;int t = 1;
// cin >> t;while(t--){solve();}
}
//3 F
//5 B
//6 F
//9 F
//10 B
//12 F
//15 FB
//18 FB
相关文章:

I - 太阳轰炸(组合数学Cnk n固定)
2023河南省赛组队训练赛(二) - Virtual Judge (vjudge.net) 背景:阿塔尼斯,达拉姆的大主教,在艾尔又一次沦陷之后指挥着星灵的最后一艘方舟舰:亚顿之矛。作为艾尔星灵数千年来的智慧结晶,亚顿之…...
centos安装gitlab
更新系统 sudo yum -y update安装所需要的包 sudo yum -y install epel-release curl vim policycoreutils-python如果要安装并使用本地Postfix服务器发送通知,请安装Postfix,这里就不安装了: sudo yum -y install postfix安装后启动并启用…...
)
【洛谷 P1093】[NOIP2007 普及组] 奖学金 题解(结构体排序)
[NOIP2007 普及组] 奖学金 题目描述 某小学最近得到了一笔赞助,打算拿出其中一部分为学习成绩优秀的前 555 名学生发奖学金。期末,每个学生都有 333 门课的成绩:语文、数学、英语。先按总分从高到低排序,如果两个同学总分相同,再…...
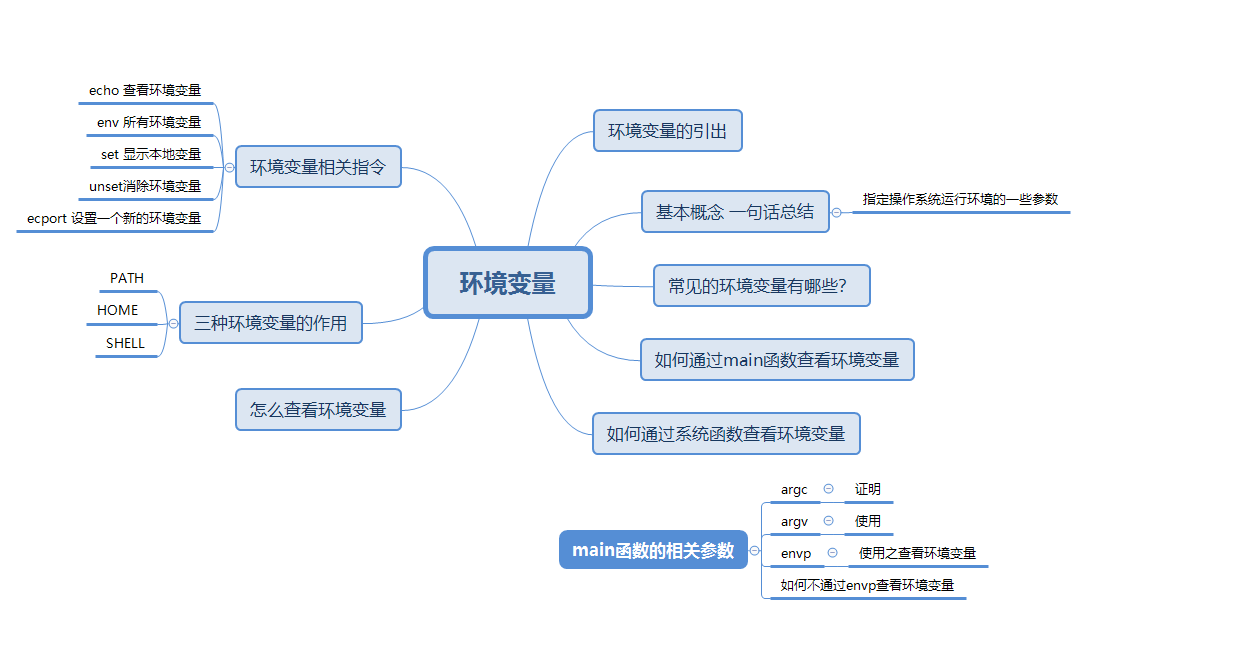
【Hello Linux】进程优先级和环境变量
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:简单介绍下进程的优先级 环境变量 进程优先级环境变量进程的优先级基本概念如何查看优先级PRI与NINI值的设置范围NI值如何修改修改方式…...

日期:Date,SimpleDateFormat常见API以及包装类
一.Date类 package com.gch.d1_date;import java.util.Date;/**目标:学会使用Date类处理时间,获取时间的信息*/ public class DateDemo1 {public static void main(String[] args) {// 1.创建一个Date类的对象:代表系统此刻日期时间对象Date d new Date();System.out.println(…...
嵌入式之ubuntu终端操作与shell常用命令详解
目录 文件和目录列表 基本列表功能 显示列表长度 过滤输出列表 浏览文件系统 Linux 文件系统 遍历目录 处理文件 创建文件 复制文件 制表键自动补全 重命名文件 删除文件 处理目录 创建目录 删除目录 编辑其他常用命令与操作 Uname命令 clear命令 返回上一级命令 显…...

【Shell学习笔记】6.Shell 流程控制
前言 本章介绍Shell的流程控制。 Shell 流程控制 和 Java、PHP 等语言不一样,sh 的流程控制不可为空,如(以下为 PHP 流程控制写法): 实例 <?php if (isset($_GET["q"])) {search(q); } else {// 不做任何事情 }在 sh/bash…...
27k入职阿里测开岗那天,我哭了,这5个月付出的一切总算没有白费~
先说一下自己的个人情况,计算机专业,16年普通二本学校毕业,经历过一些失败的工作经历后,经推荐就进入了华为的测试岗,进去才知道是接了个外包项目,不太稳定的样子,可是刚毕业谁知道什么外包不外…...

服务端开发之Java备战秋招面试篇5
努力了那么多年,回头一望,几乎全是漫长的挫折和煎熬。对于大多数人的一生来说,顺风顺水只是偶尔,挫折、不堪、焦虑和迷茫才是主旋律。我们登上并非我们所选择的舞台,演出并非我们所选择的剧本。继续加油吧! 目录 1.ArrayList与LinkedList区别, 应用场景…...

有趣的 Kotlin 0x11: joinToString,你真的了解嘛?
前言 之前使用 joinToString 函数也就是用逗号连接集合元素形成字符串,也没有细看它的参数,但是今天和 ChatGPT 聊天时,发现它给我输出了诸多内容。 joinToString joinToString()是Kotlin中一个非常有用的函数,它可以将集合的元…...
代码随想录算法训练营day46 | 动态规划之背包问题 139.单词拆分
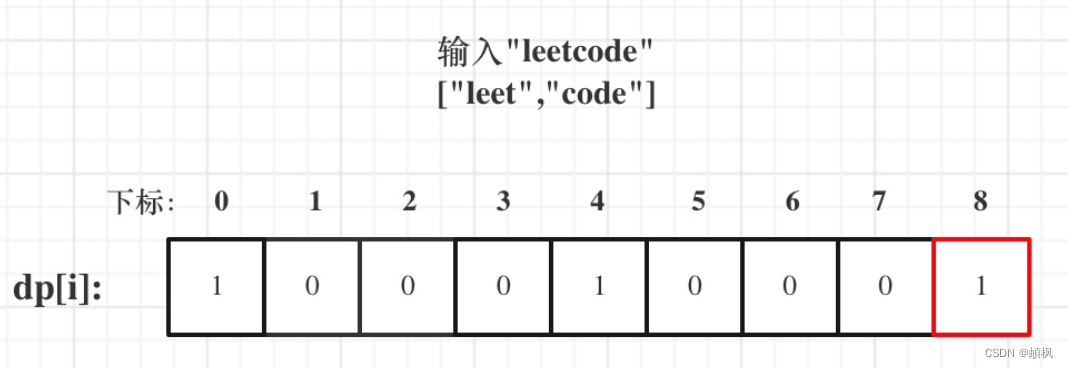
day46139.单词拆分1.确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp[i]139.单词拆分 题目链接 解题思路:单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满。…...

DPDK中的无锁共享数据结构
目录背景解决方法共享内存无锁操作新/老共享数据结构rte_ringrefcnt延迟释放方法1:读的线程来释放方法2:释放线程等到读线程轮询一轮参考背景 dpvs多线程,如何做到节约内存、高性能之间的均衡。 解决方法 共享内存 多线程共享内存&#x…...
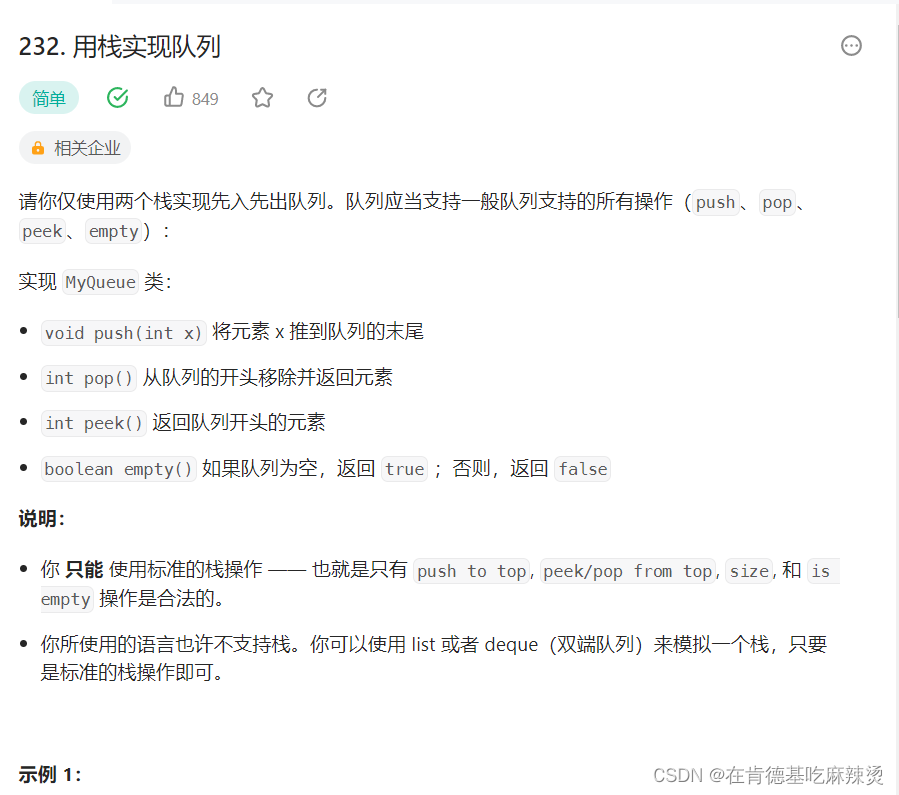
【使用两个栈实现队列】
文章目录一、栈和队列的基本特点二、基本接口函数的实现1.栈的接口2.创建队列骨架3.入队操作4.取出队列元素5.返回队首元素6.判断队列是否为空7.销毁队列总结一、栈和队列的基本特点 栈的特点是后进先出,而队列的特点是先进先出。 使用两个栈实现队列,必…...
web,h5海康视频接入监控视频流记录一
项目需求,web端实现海康监控视频对接接入,需实现实时预览,云台功能,回放功能。 web端要播放视频,有三种方式,一种是装浏览器装插件,一种是装客户端exe,还有就是无插件了。浏览器装插…...

做毕业设计,前端部分你需要掌握的6个核心技能
其实前端新手如果想要自己实现一套毕业设计项目并非简单的事,因为之前很多人一直还停留在知识点的阶段,而且管理系统和C端网站都需要开发,但现在需要点连成线了。所以在启动项目开发之前呢,针对前端部分,我列举一些非常…...
--EventLoop and thread model)
Read book Netty in action(Chapter VIII)--EventLoop and thread model
前言 简单地说,线程模型指定了操作系统、编程语言、框架或者应用程序的上下文中的线程管理的关键方面。显而易见地,如何以及何时创建线程将对应用程序代码的执行产生显著的影响,因此开发人员需要理解与不同模型相关的权衡。无论是他们自己选…...
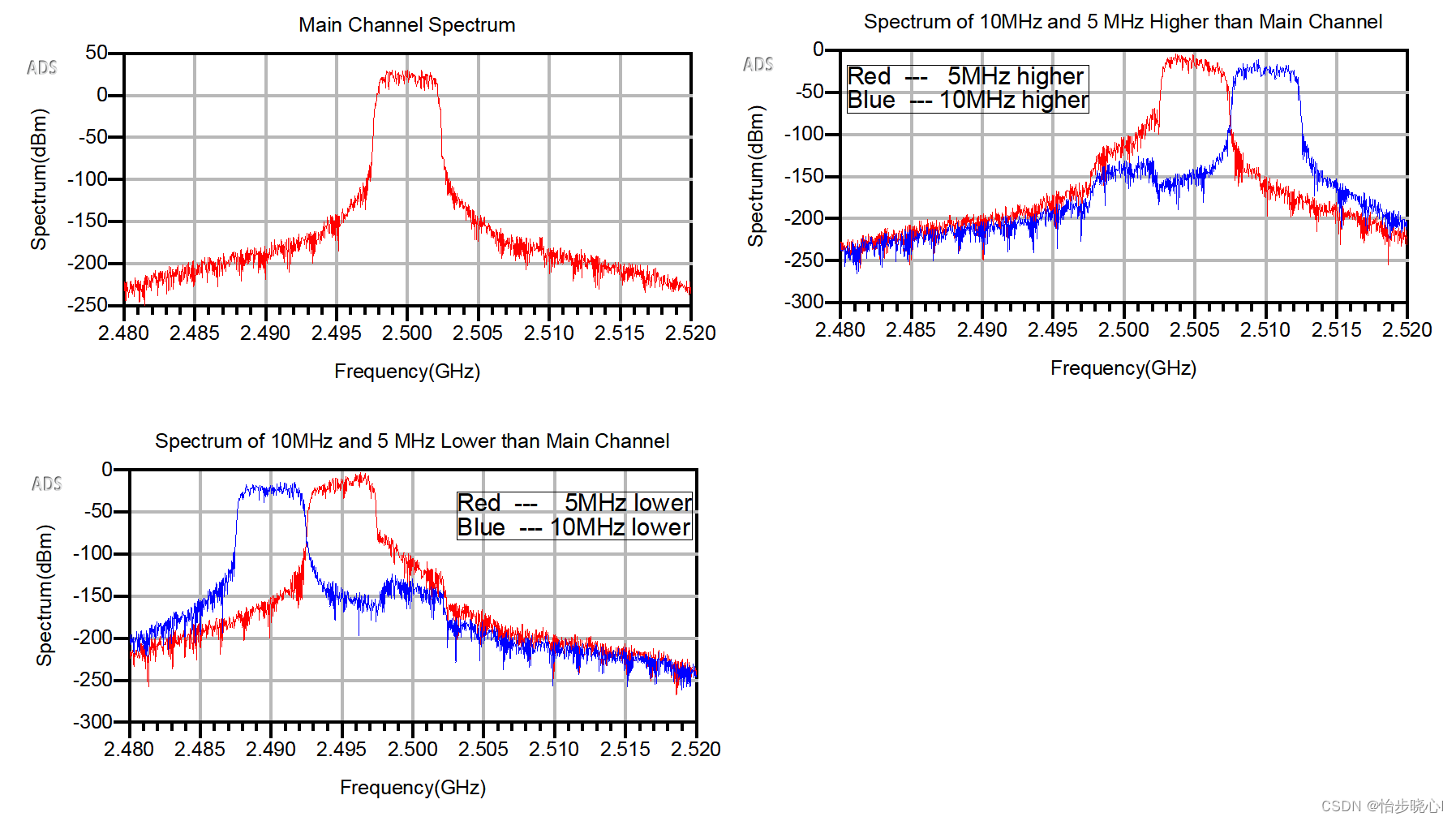
番外11:使用ADS对射频功率放大器进行非线性测试3(使用带宽5MHz的WCDMA信号进行ACLR测试)
番外11:使用ADS对射频功率放大器进行非线性测试3(使用带宽5MHz的WCDMA信号进行ACLR测试) 其他测试: 番外9:使用ADS对射频功率放大器进行非线性测试1(以IMD3测试为例) 番外10:使用AD…...

Linux libpqxx 库安装及使用
记录一下linux安装 libpqxx遇到的一些问题 1.准备安装包: 1.准备安装包,以libpqxx-4.0.1.tar.gz为例子 链接如下:https://launchpad.net/libpqxx/milestone/4.0.1 2.上传并安装 上传到安装目录并安装,我是放到/use/local下面 c…...

如何使用COM-Hunter检测持久化COM劫持漏洞
关于COM-Hunter COM- Hunter是一款针对持久化COM劫持漏洞的安全检测工具,该工具基于C#语言开发,可以帮助广大研究人员通过持久化COM劫持技术来检测目标应用程序的安全性。 关于COM劫持 微软在Windows 3.11中引入了(Component Object Model, COM)&…...

Cartesi 举办的2023 黑客马拉松
Cartesi 是具有 Linux 运行时的特定于应用程序的Rollups执行层。Cartesi 的特定应用程序 Optimistic Rollup 框架使区块链堆栈足够强大,开发人员可以构建计算密集型和以前不可能的去中心化实例。Cartesi 的 RISC-V 虚拟机支持 Linux 运行时环境,允许像你…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
