【matlab】QR分解
QR分解
给定一个m×n的矩阵A,其中m≥n,即矩阵A是高矩阵或者是方阵,QR分解将矩阵A分解为两个矩阵Q和R的乘积,其中矩阵Q是一个m×n的各列正交的矩阵,即QTQ=I,矩阵R是一个n×n的上三角矩阵,其对角线元素为正。
如果矩阵A是方阵,且各列线性无关,那么Q是一个正交矩阵,即QTQ=QQT=I。
QR分解有多种算法实现,包括Gram-Schmidt正交化方法、Householder变换方法和Givens旋转方法等,下面我们介绍Gram-Schmidt正交化方法和Householder变换方法,并在MATLAB平台上使用这两种算法来实现QR分解。
Gram-Schmidt算法
对于给定的n维向量a1,a2,……,an,Gram-Schmidt算法可以解决将其标准正交化的问题,即将一个线性无关的向量组转化为一个正交向量组,使得每个向量都与前面的向量正交(垂直),并且可以检验a1,a2,……,an是否是线性相关。
Gram-Schmidt算法的步骤如下:
- 初始化n维向量q1,q2,……,qn,其中q1=a1/||a1||2。
- 对于每个向量ai,i=2:n,进行正交化处理:qi= ai-( q1Tai)q1-…-( qi-1Tai)qi-1。
- 如果qi=0,说明ai是a1,a2,……,ai-1的一个线性组合,可以结束算法了。
- 否则将qi进行单位化,qi=qi/||qi||2。
如果步骤③没有结束,那么说明a1,a2,……,an是线性无关的,而且得到了一个正交向量组q1,q2,……,qn。
Gram-Schmidt算法实现的QR分解
对于给定矩阵A,其列向量线性无关,Gram-Schmidt算法实现的QR分解步骤如下:
- 对列向量a1,a2,……,an按照Gram-Schmidt方法进行正交化。
- 对上一步得到的正交化向量组进行单位化得到各列正交的矩阵Q。
- 根据A=QR,QTQ=I→R=QTA,得到上三角矩阵R
MATLAB验证Gram-Schmidt算法实现QR分解稳定性
通过直观的方法来观察到Gram-Schmidt QR分解的正交性偏差,理论上通过Gram-Schmidt算法后可以得到列向量线性无关的各列正交的矩阵Q,即QTQ=I,我们可以直接计算QTQ,看看计算结果与单位矩阵I的差距
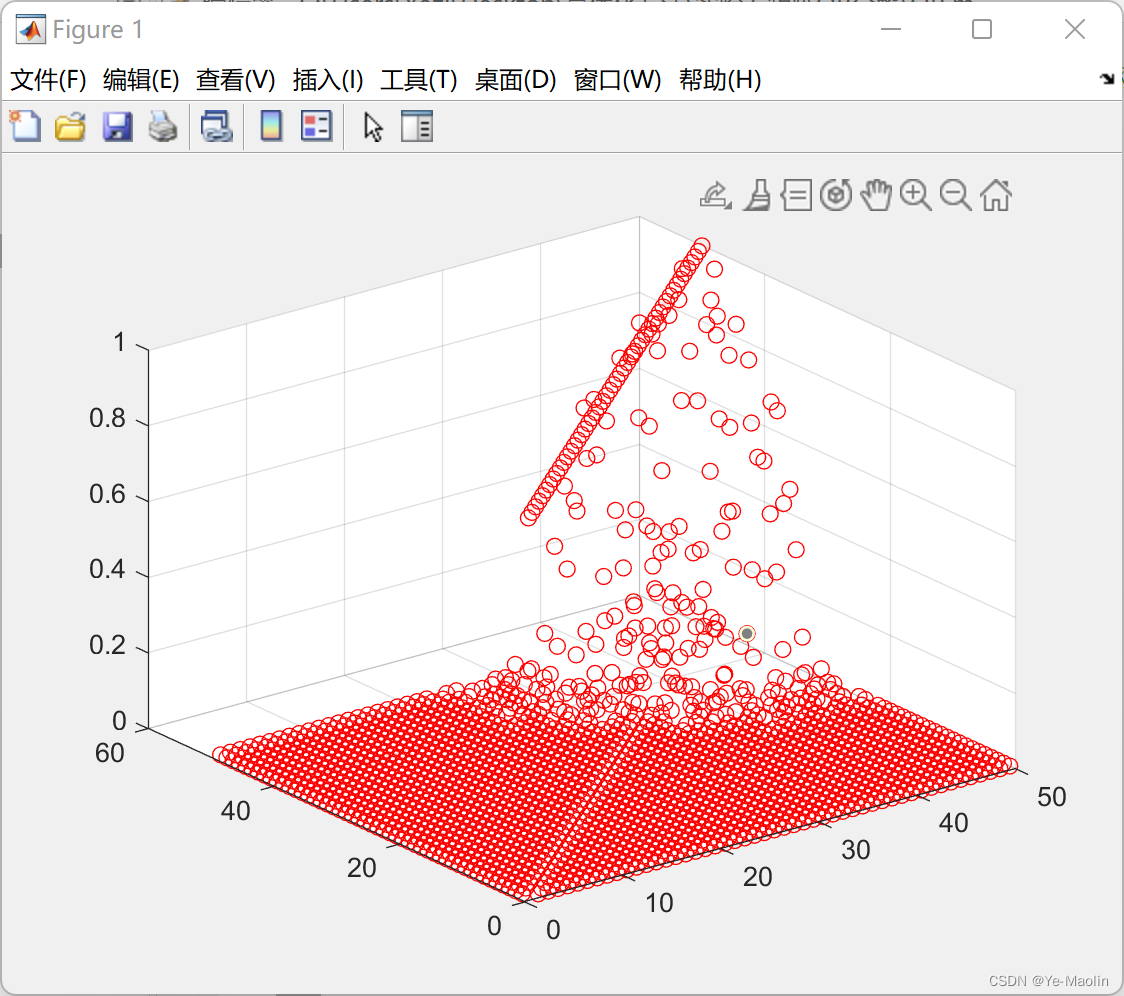
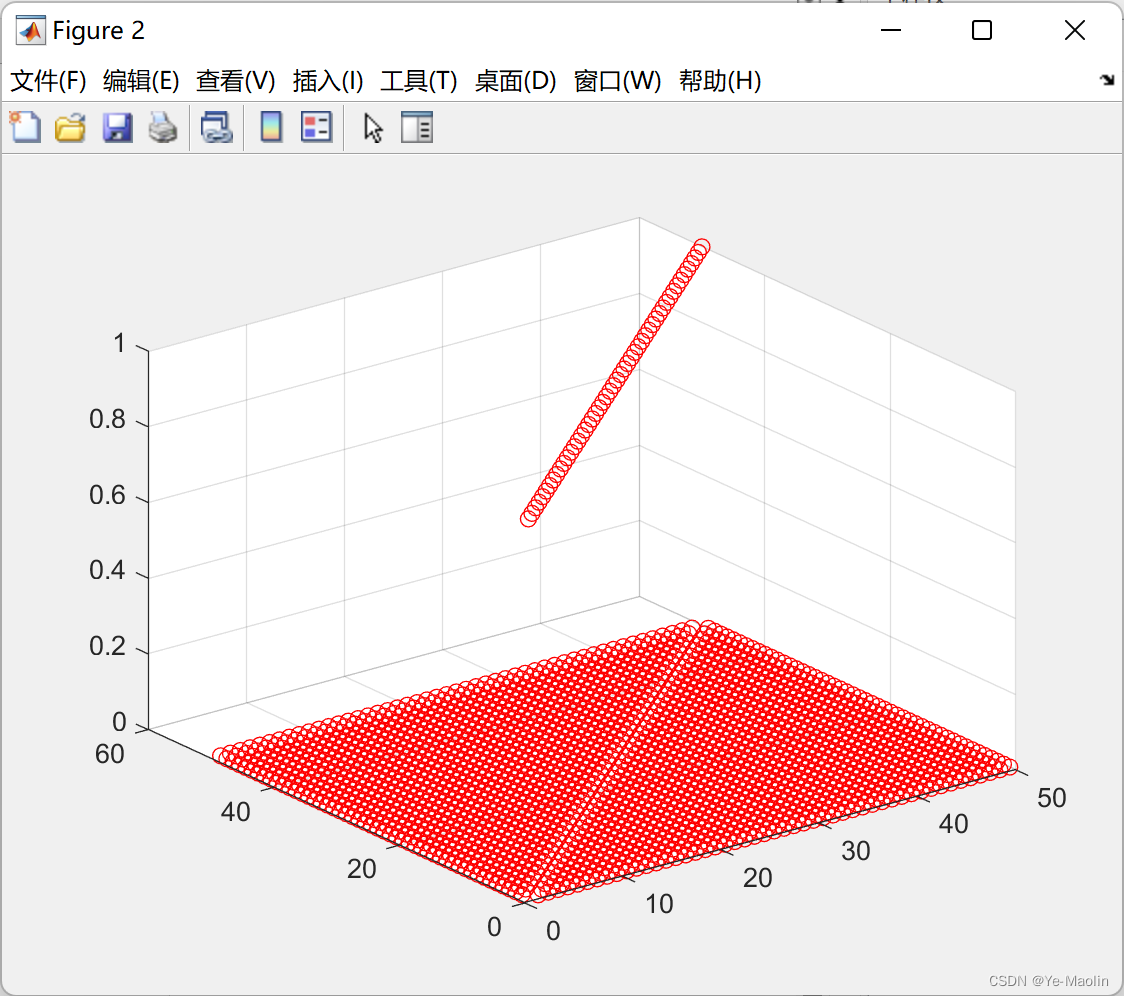
左图是QTQ的计算结果,有图是单位矩阵I,可见由于浮点数存储的舍入误差,随着k增大,积累的误差越大,矩阵Q逐渐失去正交性
clc,clear;
load MatrixA.mat;
[m,n]=size(A);
Q=zeros(m,n);
R=zeros(n,n);
%% Gram-Schmidt QR分解
for k=1:nR(1:k-1,k)=Q(:,1:k-1)'*A(:,k); %求出R(1,K) - R(K-1,K)v=A(:,k)-Q(:,1:k-1)*R(1:k-1,k); %求出正交化向量qR(k,k)=norm(v); %求出R(K,K)Q(:,k)=v/R(k,k); %单位化向量q
end
%% 正交性偏差
figure(1);
E = zeros(1,n);
for k=2:nmax = 0;for i=1:k-1temp = abs(Q(:,i)' * Q(:,k));if temp > maxmax = temp;endendE(1,k)=max;
end
plot(E)
%% 比较QTQ和I
QTQ=Q'*Q;
figure(2);
for i=1:nfor j=1:nscatter3(i,j,QTQ(i,j),'red');hold on;end
end
zlim([0,1]);
I=eye(n);
figure(3);
for i=1:nfor j=1:nscatter3(i,j,I(i,j),'red');hold on;end
end
zlim([0,1]);Householder变换
Householder变换是一种镜面反射变换,householder变换矩阵为H = I - 2wwT,如何理解这个变换矩阵呢,考虑向量w,那么有:
Hw = (I - 2wwT)w = w - 2w(wTw) = - w
这说明对于平行于w的向量,householder变换的作用是将其反向,再考虑与向量w垂直的向量v,即wTv=0,那么有:
Hv = (I - 2wwT)v = v - 2w(wTv) = v
这说明对于垂直于w的向量,householder变换的作用就是对其不起任何作用,那么对于一个普通的向量v来说,平行于w的分量被householder反向,垂直于w的分量不变,那么最终的效果就是将向量v作关于法向量为w的平面的镜像对称
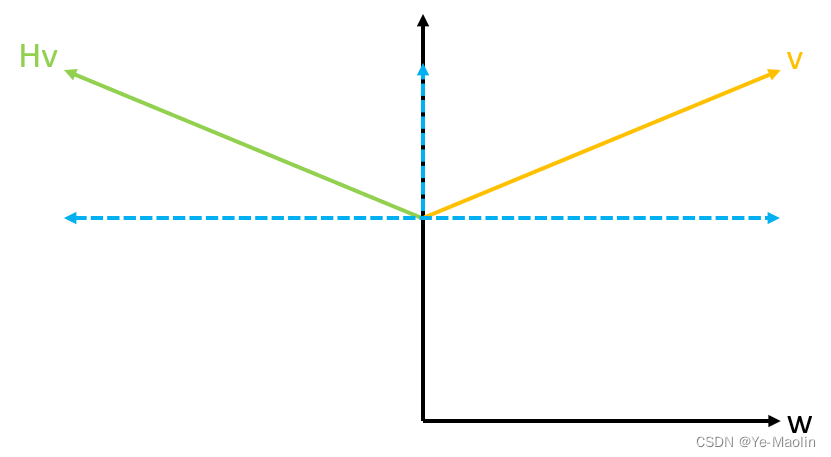
基于Householder变换的QR分解

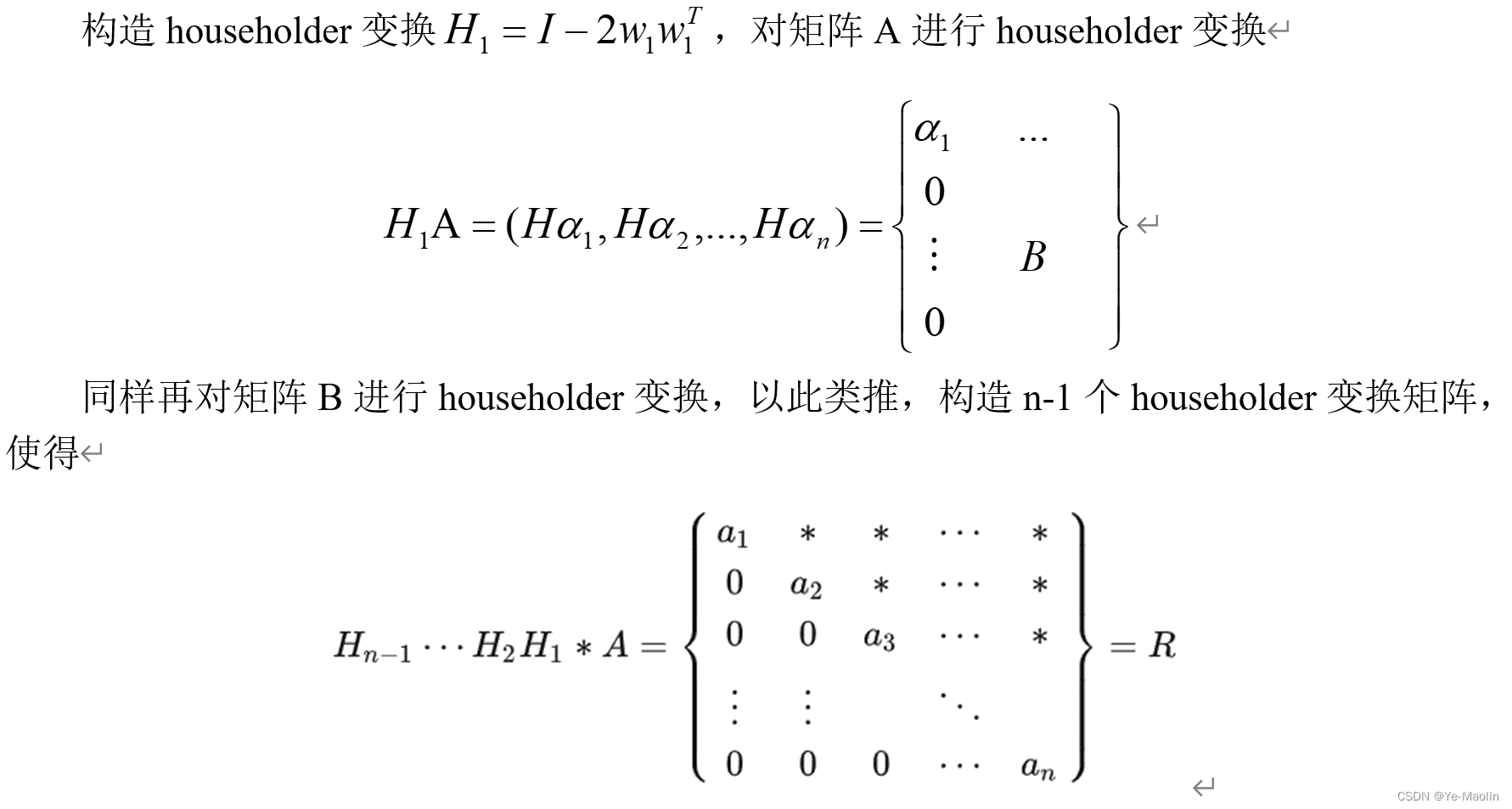
因为H=H-1,所以A=H1H2,…,Hn-1R,即Q= H1H2,…,Hn-1,再根据A=QR,QTQ=I→R=QTA。
再来比较一下QTQ与单位矩阵I的差距,结果如图所示,左边的是计算出来的QTQ,右边是单位矩阵I

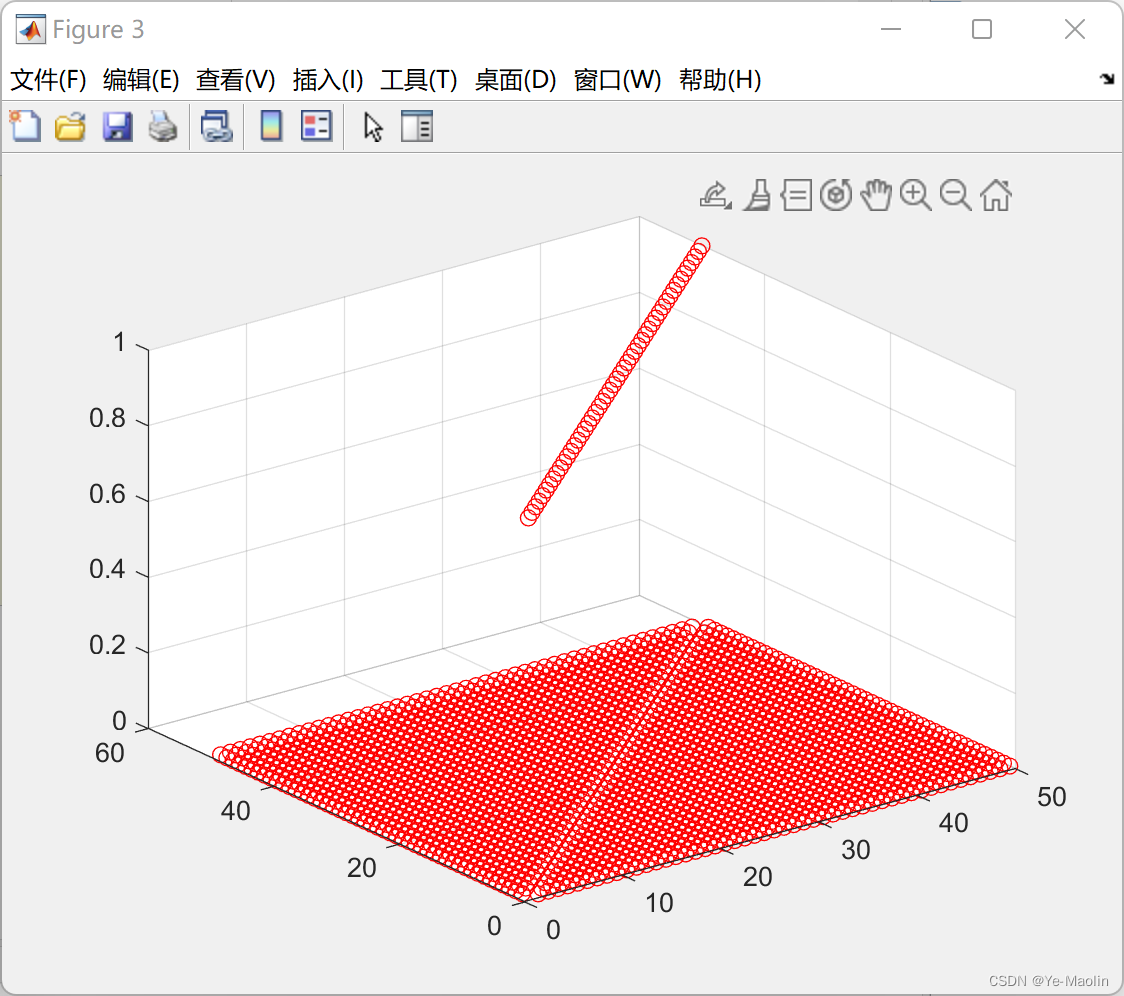
结果QTQ和I基本一样,可见相比其他分解方法,Householder算法能够减小舍入误差的累积,提高计算结果的稳定性。此外,该算法的时间复杂度较低,具备较高的计算效率。
clc,clear;
load MatrixA.mat;
[m,n]=size(A);
Q=zeros(m,n);
R=zeros(n,n);
%% Householder QR分解
[Q,R]=qr(A); % matlab库函数就是用的Householder
%% 正交性偏差
figure(1);
E = zeros(1,n);
for k=2:nmax = 0;for i=1:k-1temp = abs(Q(:,i)' * Q(:,k));if temp > maxmax = temp;endendE(1,k)=max;
end
plot(E)
%% 比较QTQ和I
QTQ=Q'*Q;
figure(2);
for i=1:nfor j=1:nscatter3(i,j,QTQ(i,j),'red');hold on;end
end
zlim([0,1]);
I=eye(n);
figure(3);
for i=1:nfor j=1:nscatter3(i,j,I(i,j),'red');hold on;end
end
zlim([0,1]);判断矩阵是否可逆
判断矩阵是否可逆有以下几种方法:
- 存在一个矩阵B,使得AB=BA=I,确实可逆。
- 矩阵行列式不为0,可逆。
- 矩阵满秩,可逆。
- 线性方程组Ax=0只有0解,可逆。
- 线性方程组Ax=b只有特解,可逆。
实际上如果一个方阵可以进行QR分解,那么这个方阵也是可逆的。
所以我们直接尝试对矩阵B进行QR分解,如果可以进行QR分解,那么矩阵B可逆。那么我们可以先假设矩阵B是可以进行QR分解,然后我们对矩阵B进行QR分解,显然矩阵B是可以进行QR分解的,这说明矩阵B是可逆的。
求逆
我们之前使用过高斯消元法来求解矩阵的逆,实际上也可以使用QR分解求矩阵的逆。由A = QR,QTQ = I,则A-1 = (QR)-1 = R-1Q-1 = R-1QT。
那么A-1就可以通过R-1QT得到,但是实际上我们并不需要计算R-1,让x= R-1QT,那么我们目标就是要得到x的结果,因为RR-1QT=QT,即Rx=QT,那么我们就需要求解这个线性方程组,由于R是上三角矩阵,所以直接回代就可以求出x,即求出R-1QT,即求出了A-1。
我们先用Gram-Schmidt算法实现的QR分解求解矩阵B的逆,将其与用MATLAB内置的求逆函数结果进行比较,结果如图所示,红色的圆圈是matlab内置的求逆函数计算出来的结果,绿色实心点是我们QR分解求出来的结果,如果二者重合说明计算结果相同。

可以看到基本上绿色的点都和红色的圆圈重合了,可见Gram-Schmidt算法QR分解求逆效果不错。
clc,clear;
load MatrixB.mat;
[m,n]=size(B);
Q=zeros(m,n);
R=zeros(n,n);
%% Gram-Schmidt QR分解
for k=1:nR(1:k-1,k)=Q(:,1:k-1)'*B(:,k); %求出R(1,K) - R(K-1,K)v=B(:,k)-Q(:,1:k-1)*R(1:k-1,k); %求出正交化向量qR(k,k)=norm(v); %求出R(K,K)Q(:,k)=v/R(k,k); %单位化向量q
end
%% 求逆
inverseQR=R\Q';
inverse=inv(B);
%% 画图比较
for i=0:n-1for j=1:nscatter(i*n+j,inverse(i+1,j),'red');hold on;scatter(i*n+j,inverseQR(i+1,j),'green','.');hold on;end
end我们再用之前的高斯消元法求解矩阵B的逆,将其与用MATLAB内置的求逆函数结果进行比较,结果如图所示
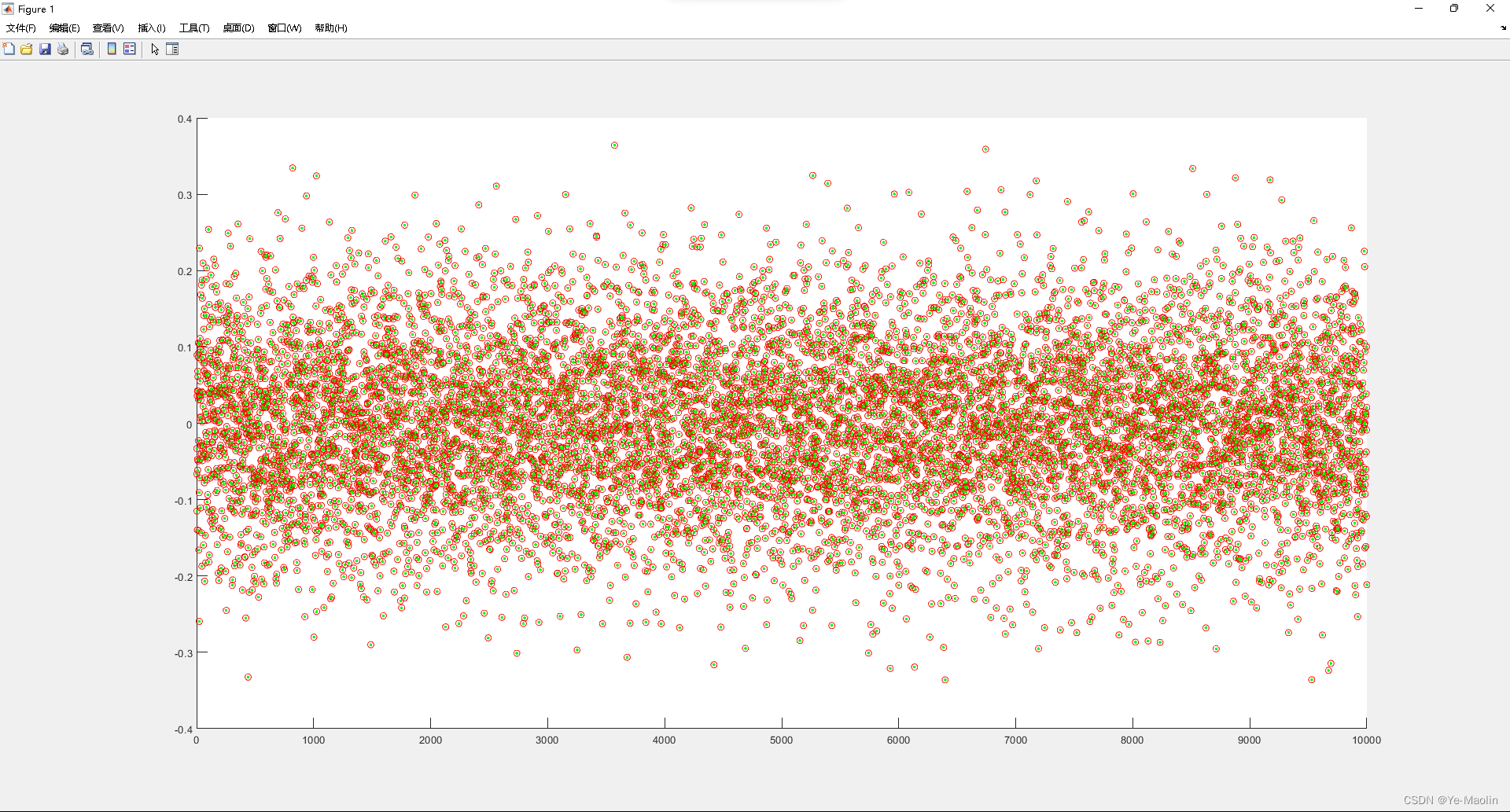
可见高斯消元法求逆的结果也很好,基本上绿色的点都和红色的圆圈重合了。
clc,clear;
load MatrixB.mat;
b=eye(50);
B_b=[B,b];
[n,m]=size(B_b);
for i=1:nfor j=m:-1:iB_b(i,j)=B_b(i,j)/B_b(i,i);endfor j=i+1:nfor k=m:-1:iB_b(j,k)=B_b(j,k)-B_b(j,i)*B_b(i,k);endend
% fprintf('第%d次消元\n',i);
% disp(rats(A_b));
end
for i=n-1:-1:1for j=i:-1:1for k=m:-1:n+1B_b(j,k)=B_b(j,k)-B_b(j,i+1)*B_b(i+1,k);endB_b(j,i+1)=0;end
% fprintf('第%d次回代\n',n-i);
% disp(rats(A_b));
end
gaussInverse=B_b(:,end-49:end);
inverse=inv(B);
%% 画图比较
for i=0:n-1for j=1:nscatter(i*n+j,inverse(i+1,j),'red');hold on;scatter(i*n+j,gaussInverse(i+1,j),'green','.');hold on;end
end再用householder算法实现的QR分解求解矩阵B的逆,将其与用MATLAB内置的求逆函数结果进行比较,结果如图所示。
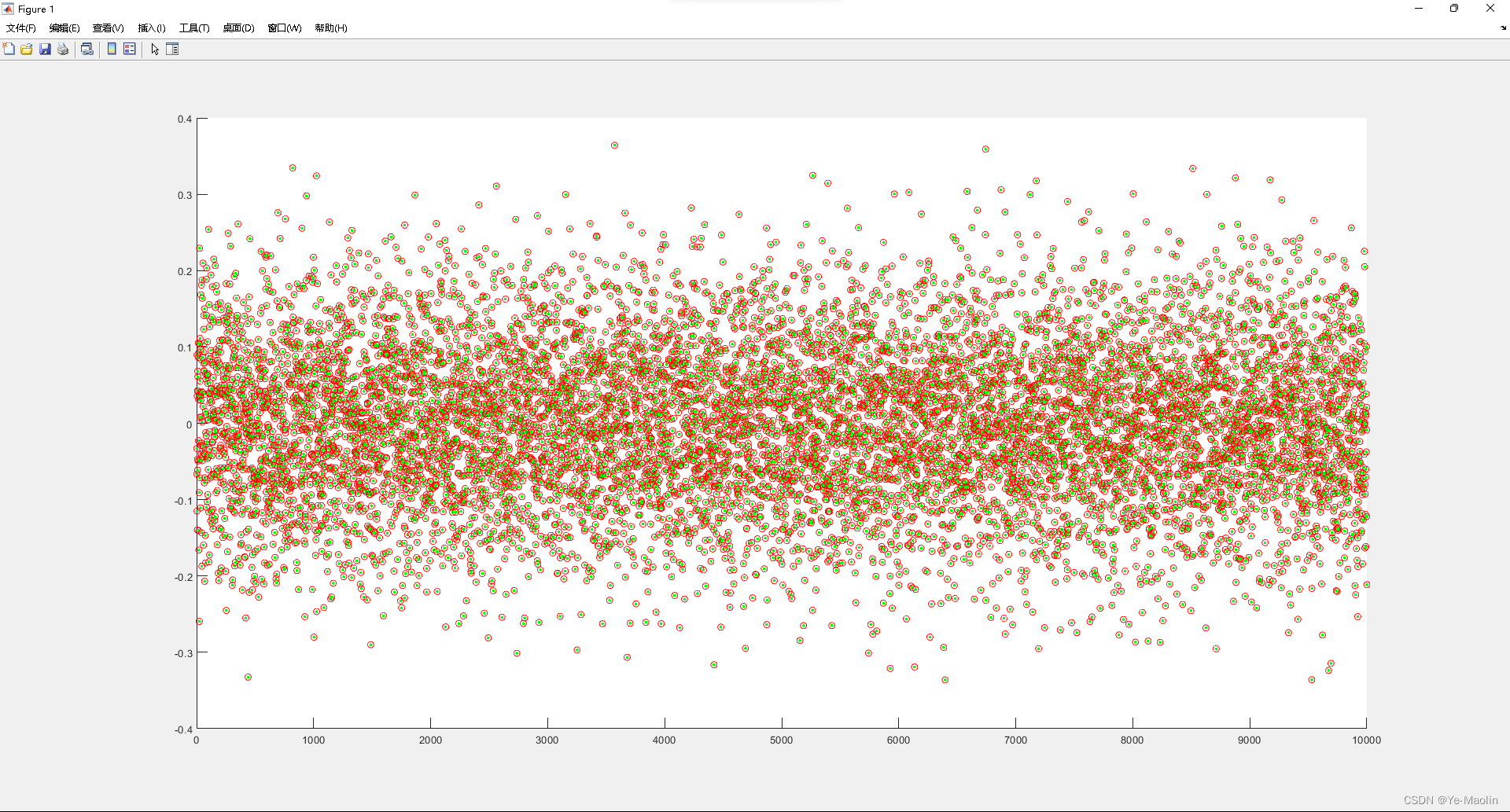
可见householder实现的QR分解求逆结果效果很好,基本上和matlab内置求逆函数结果相同,速度上也不慢。
clc,clear;
load MatrixB.mat;
[m,n]=size(B);
Q=zeros(m,n);
R=zeros(n,n);
%% Householder QR分解
[Q,R]=qr(B); % matlab库函数就是用的Householder
%% 求逆
inverseQR=R\Q';
inverse=inv(B);
%% 画图比较
for i=0:n-1for j=1:nscatter(i*n+j,inverse(i+1,j),'red');hold on;scatter(i*n+j,inverseQR(i+1,j),'green','.');hold on;end
end相关文章:

【matlab】QR分解
QR分解 给定一个mn的矩阵A,其中m≥n,即矩阵A是高矩阵或者是方阵,QR分解将矩阵A分解为两个矩阵Q和R的乘积,其中矩阵Q是一个mn的各列正交的矩阵,即QTQI,矩阵R是一个nn的上三角矩阵,其对角线元素为…...
Liunx系统使用超详细(三)
本篇内容开始逐渐描述有关liunx的各种命令的使用方法! 目录 一、目录和文件区别 1.1目录: 1.2文件: 1.3总结: 二、Linux命令的写法 三、linux命令清屏 四、pwd命令 五、ls命令 5.1 ls: 5.2 ls -l:…...

Kubernetes学习笔记-Part.06 Docker安装
目录 Part.01 Kubernets与docker Part.02 Docker版本 Part.03 Kubernetes原理 Part.04 资源规划 Part.05 基础环境准备 Part.06 Docker安装 Part.07 Harbor搭建 Part.08 K8s环境安装 Part.09 K8s集群构建 Part.10 容器回退 第六章 Docker安装 在master、worker、harbor上均需…...

现在的00后,实在是太卷了......
现在的小年轻真的卷得过分了。前段时间我们公司来了个00年的,工作没两年,跳槽到我们公司起薪18K,都快接近我了。后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。 最近和他聊了一次天,原来这位小老弟家里条…...

Maven项目目录结构
项目结构 目录说明.ideaIDEA工具的配置文件.mvn用于运行Maven项目src源码文件夹target字节码文件夹.gitignore配置git忽略文件HELP.md自述文件mvnw运行Maven命令(Linux)mvnw.cmd运行Maven命令(Windows)pom.xml依赖管理文件 如图…...
感慨!一路从测试小白到现在的高级测试工程师,方向不对真的很艰辛
1 功能测试人员,也就是我们常常俗称的进行点点点测试工程师。前 1-2 年做功能测试,使用其他人开发的工具进行测试。这个阶段的测试工作都比较初级,严重依赖于别人开发的工具和系统。当系统进行升级换代的时候,强哥会明显的感觉到…...
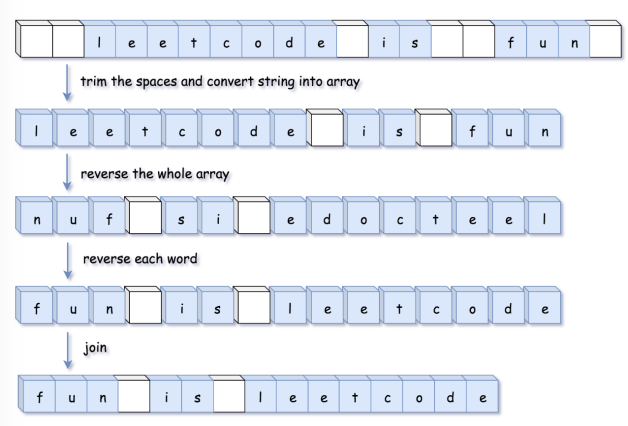
字符串经典基础面试题
关卡名 字符串经典基础面试题 我会了✔️ 内容 1.理解字符串反转的处理方法 ✔️ 2.熟练掌握回文串的判断方法 ✔️ 3.掌握字符串中搜索第一个唯一字符的方法 ✔️ 4.掌握判断是否互为字符串重排的处理技巧 ✔️ 1 反转的问题 我们知道反转是链表的一个重要考点…...

【华为OD题库-062】计算礼品发放的最小分组数目-java
题目 又到了一年的末尾,项目组让小明负责新年晚会的小礼品发放工作。为使得参加晚会的同时所获得的小礼品价值相对平衡,需要把小礼品根据价格进行分组,但每组最多只能包括两件小礼品,并且每个分组的价格总和不能超过一个价格上限。…...

[go 面试] 构建高效微服务通信:选择合适的通信方式
关注公众号【爱发白日梦的后端】分享技术干货、读书笔记、开源项目、实战经验、高效开发工具等,您的关注将是我的更新动力! 构建分布式系统或微服务架构时,服务间通信成为至关重要的一环。不同的通信方式各有优劣,因此在选择时需根…...

【华为OD题库-048】拔河比赛-java
题目 公司最近准备进行拔河比赛,需要在全部员工中进行挑选。选拔的规则如下: 1.按照身高优先、体重次优先的方式准备比赛阵容 2.规定参赛的队伍派出10名选手 请实现一个选拔队员的小程序。 输入为一个数组,记录了部门人员的身高、体重信息,如…...
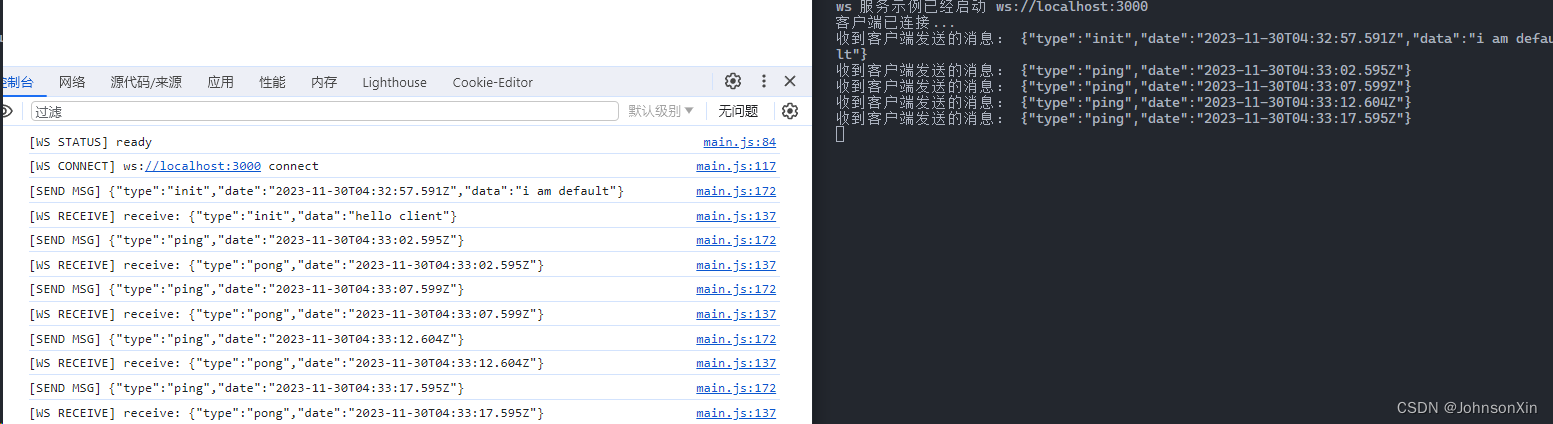
【WebSocket】通信协议基于 node 的简单实践和心跳机制和断线重连的实现
前后端 WebSocket 连接 阮一峰大佬 WebSocket 技术博客 H5 中提供的 WebSocket 协议是基于 TCP 的全双工传输协议。它属于应用层协议,并复用 HTTP 的握手通道。它只需要一次握手就可以创建持久性的连接。 那么什么是全双工呢? 全双工是计算机网络中的…...
【有ISSN、ISBN号!往届均已完成EI检索】第三届电子信息工程、大数据与计算机技术国际学术会议(EIBDCT 2024)
第三届电子信息工程、大数据与计算机技术国际学术会议(EIBDCT 2024) 2024 3rd International Conference on Electronic Information Engineering, Big Data and Computer Technology 第三届电子信息工程、大数据与计算机技术国际学术会议(…...
【Windows】使用SeaFile搭建本地私有云盘并结合内网穿透实现远程访问
1. 前言 现在我们身边的只能设备越来越多,各种智能手机、平板、智能手表和数码相机充斥身边,需要存储的数据也越来越大,一张手机拍摄的照片都可能有十多M,电影和视频更是按G计算。而智能设备的存储空间也用的捉襟见肘。能存储大量…...
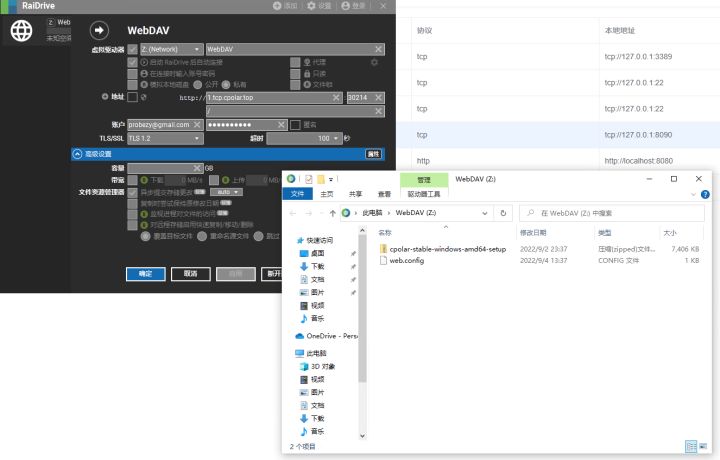
Windows本地搭建WebDAV服务并使用内网穿透远程访问【无公网IP】
windows搭建WebDAV服务,并内网穿透公网访问【无公网IP】 文章目录 windows搭建WebDAV服务,并内网穿透公网访问【无公网IP】1. 安装IIS必要WebDav组件2. 客户端测试3. cpolar内网穿透3.1 打开Web-UI管理界面3.2 创建隧道3.3 查看在线隧道列表3.4 浏览器访…...

责任链设计模式
package com.jmj.pattern.responsibility;/*** 请假条类*/ public class LeaveRequest {//姓名private String name;//请假天数private int num;//请假内容private String content;public LeaveRequest(String name, int num, String content) {this.name name;this.num num;…...
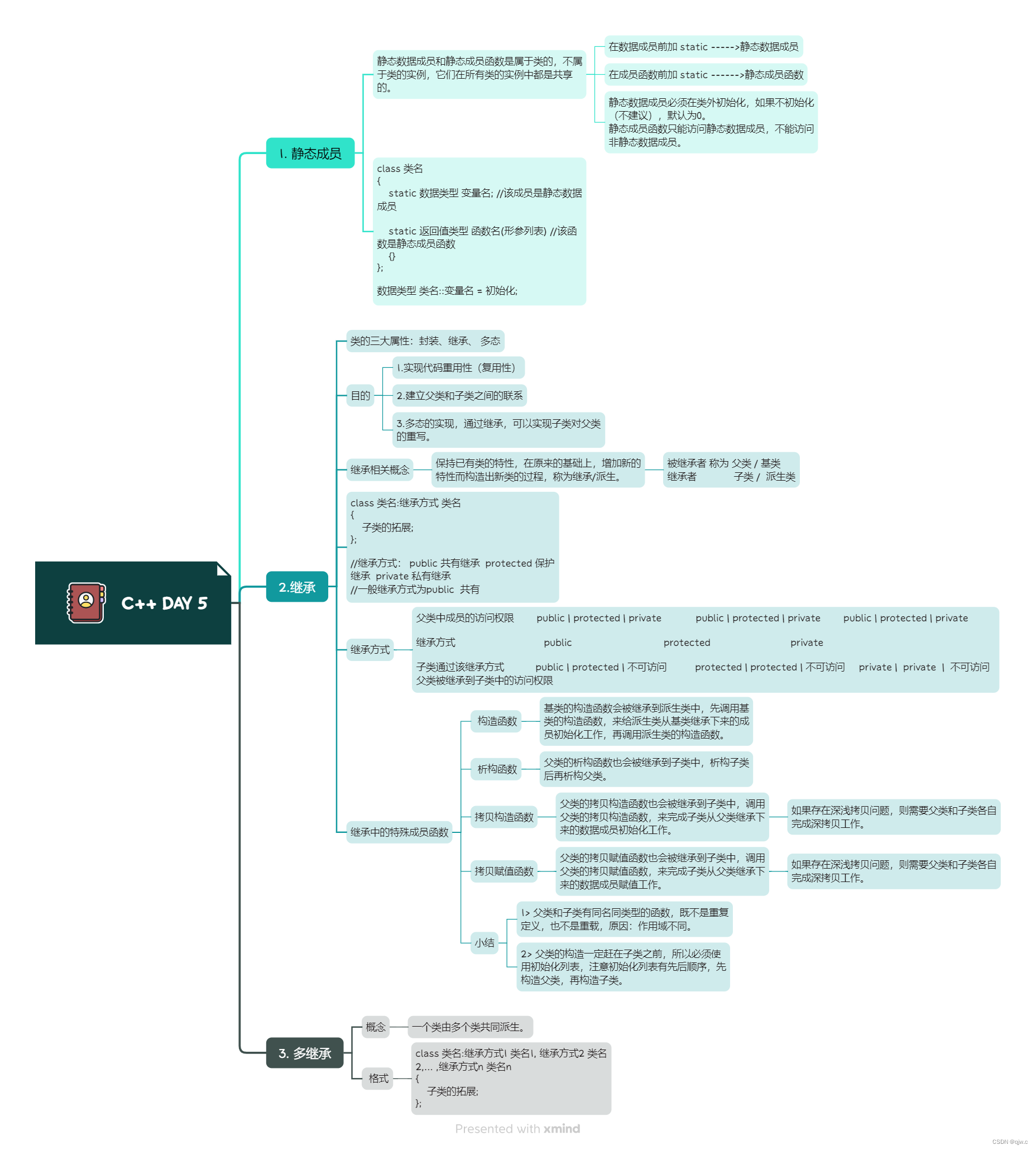
12.4 C++ 作业
完成沙发床的多继承 #include <iostream>using namespace std;//封装 沙发 类 class Sofa { private:string *sitting; public://无参构造函数Sofa(){cout << "Sofa::无参构造函数" << endl;}//有参构造函数Sofa(string s):sitting(new string(s)…...

基于ssm品牌会员在线商城源码
基于ssm品牌会员在线商城源码708 idea mysql数据库 navcat 开发技术:后端 ssm 后台管理 vue 用户端 vue.jshtml 演示视频: 基于ssm品牌会员在线商城源码 DROP TABLE IF EXISTS address; /*!40101 SET saved_cs_client character_set_client */; /…...

骨传导耳机音量大了有害吗?骨传导能保护听力吗?
无论是传统耳机还是骨传导耳机,只要使用音量过大,都会对有一定的损伤,然而由于骨传导耳机的传声原理和佩戴方式比较特殊,所以对人体的损伤比较小,想要知道骨传导耳机能否保护听力,就要先了解骨传导耳机的传…...
百望云供应链协同解决方案入选北大创新评论产业研究案例库
11月28日-29日,百望云受邀出席《北大创新评论》2023 Inno China 中国产业创新大会,从战略构建、生态塑造、科技创新等议题出发,与学术专家、产业专家、企业代表共赴盛会,思享汇聚。会上,《北大创新评论产业研究案例库&…...

selenium中元素定位正确但是操作失败,6种解决办法全搞定
selenium中元素定位正确但是操作失败的原因无外乎以下4种: 01 页面没加载好 解决方法:添加等待方法,如:time.sleep() 02 页面提交需要等待给数据后台 解决方法:添加等待方法,如:time.sleep(…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
