比特数据结构与算法(第四章_下)二叉树OJ(力扣:144,965,104,226,100,572)
144. 二叉树的前序遍历
难度简单
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
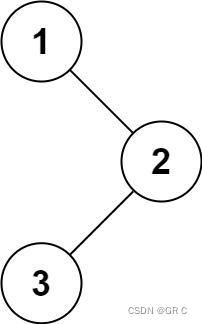
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = [ ]
输出:[ ]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
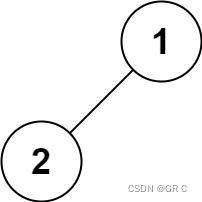
输入:root = [1,2]
输出:[1,2]
示例 5:
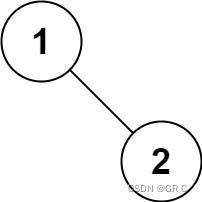
输入:root = [1,null,2]
输出:[1,2]
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
进阶:递归算法很简单,你可以通过迭代算法完成吗?
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/
int* preorderTraversal(struct TreeNode* root, int* returnSize){}解析代码:
ps(迭代算法我们要学了C++之后的高阶数据结构再实现)
int TreeSize(struct TreeNode* root)
{if(root==NULL){return 0;}return 1 + TreeSize(root->left) + TreeSize(root->right);
}void _preorderTraversal(struct TreeNode* root,int* array,int* pi) // (函数前面的_代表这个函数的子函数)
{if(root==NULL){return;}array[(*pi)++] = root->val;_preorderTraversal(root->left,array,pi);_preorderTraversal(root->right,array,pi);
}int* preorderTraversal(struct TreeNode* root, int* returnSize){int size = TreeSize(root);int* array=(int*)malloc(sizeof(int)*size);int i = 0;_preorderTraversal(root,array,&i);*returnSize=size;return array;
}(写完这题可以去写写二叉树的中序遍历和后序遍历,都是一样的)链接:
94. 二叉树的中序遍历
965. 单值二叉树
难度简单
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。
示例 1:
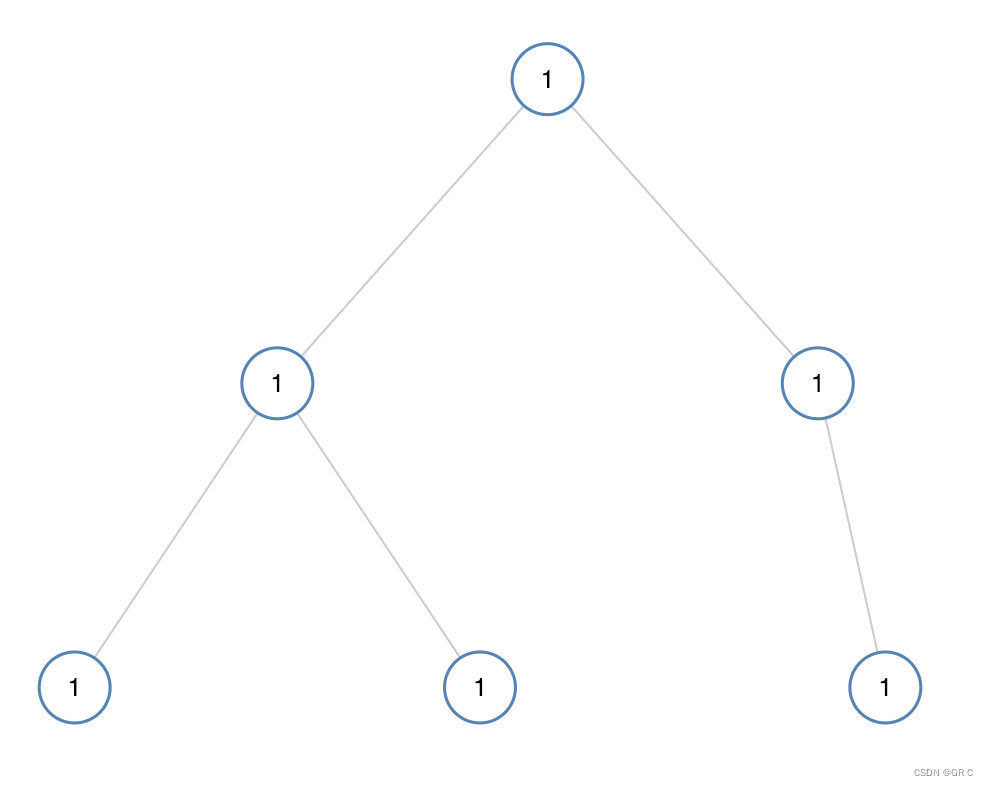
输入:[1,1,1,1,1,null,1]
输出:true
示例 2:
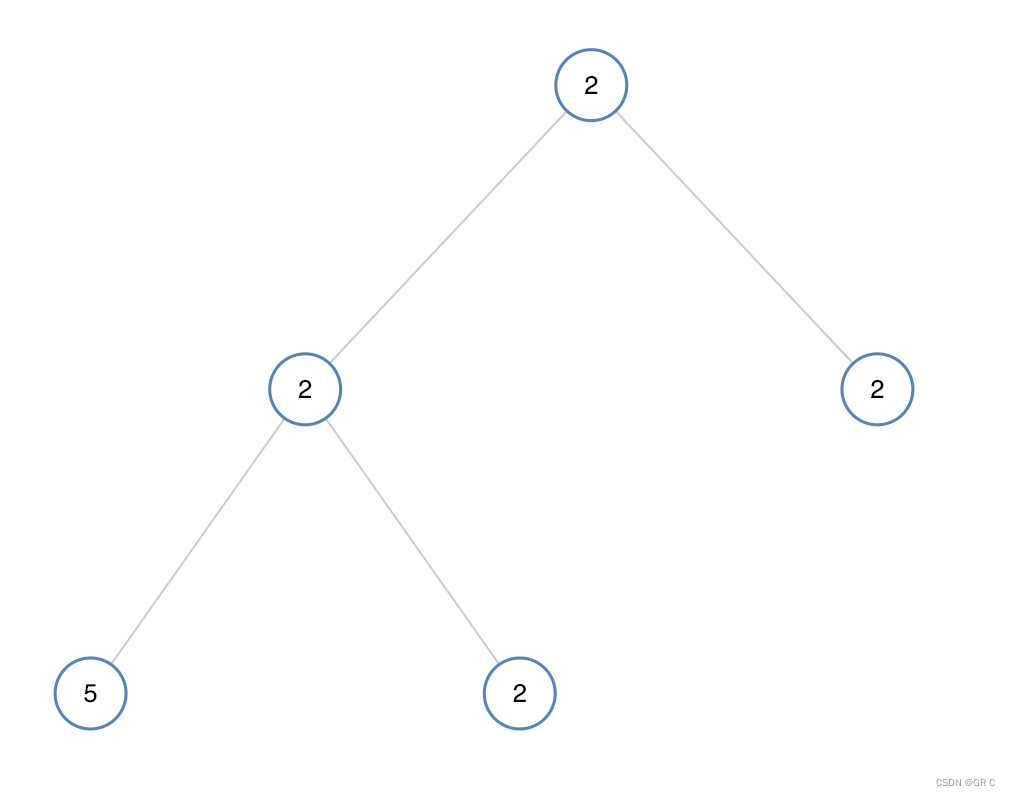
输入:[2,2,2,5,2]
输出:false
提示:
给定树的节点数范围是 [1, 100]。
每个节点的值都是整数,范围为 [0, 99] 。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/bool isUnivalTree(struct TreeNode* root){}解析代码:
bool isUnivalTree(struct TreeNode* root) {if (root == NULL){return true;}if (root->left && root->val != root->left->val){return false;}if (root->right && root->val != root->right->val){return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);
}104. 二叉树的最大深度
难度简单
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/int maxDepth(struct TreeNode* root){}解析代码:
/*int maxDepth(struct TreeNode* root) {if (root == NULL){return 0;}return maxDepth(root->left) > maxDepth(root->right) ? maxDepth(root->left) + 1 : maxDepth(root->right) + 1;
}*/ //这样写会有重复的递归计算, 优化:
int maxDepth(struct TreeNode* root) {if (root == NULL){return 0;}int leftDepth = maxDepth(root->left);int rightDepth = maxDepth(root->right);return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}226. 翻转二叉树
难度简单
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
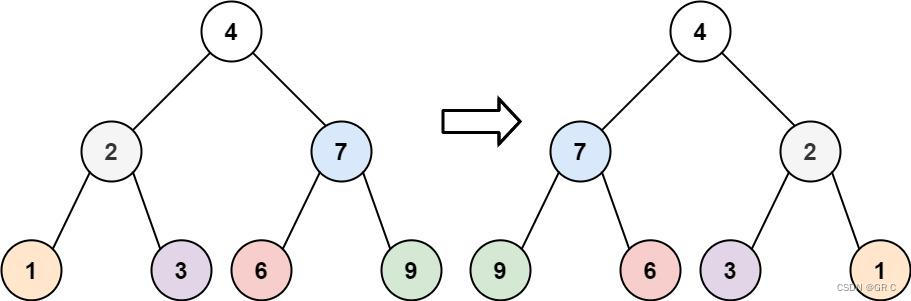
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
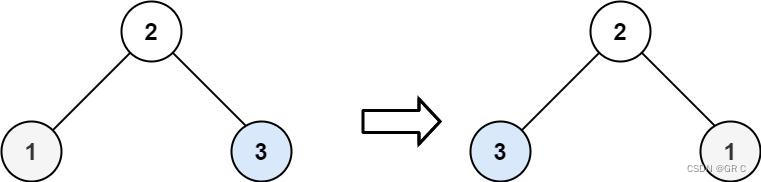
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/struct TreeNode* invertTree(struct TreeNode* root){}解析代码(法一):
struct TreeNode* invertTree(struct TreeNode* root) {if (root == NULL){return NULL;}struct TreeNode* tmp = root->left;root->left = root->right;root->right = tmp;invertTree(root->left);invertTree(root->right);return root;
}解析代码(法二):
struct TreeNode* invertTree(struct TreeNode* root) {if (root == NULL){return NULL;}struct TreeNode* rightTmp = root->right;root->right = invertTree(root->left);root->left = invertTree(rightTmp);return root;
}100. 相同的树
难度简单
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
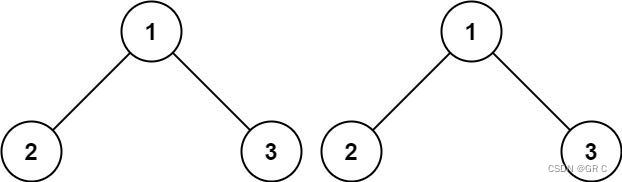
输入:p = [1,2,3], q = [1,2,3]
输出:true
示例 2:

输入:p = [1,2], q = [1,null,2]
输出:false
示例 3:
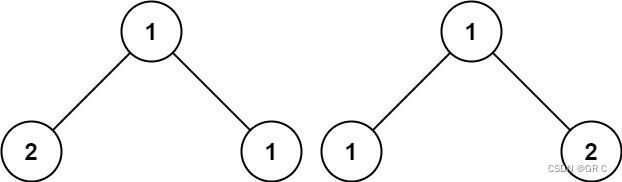
输入:p = [1,2,1], q = [1,1,2]
输出:false
提示:
两棵树上的节点数目都在范围 [0, 100] 内
-10^4 <= Node.val <= 10*4
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/bool isSameTree(struct TreeNode* p, struct TreeNode* q){}解析代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if (p == NULL && q == NULL){return true;}if (p == NULL || q == NULL)//其中一个为空,另一个不为空{return false;}if (p->val != q->val){return false;}return isSameTree(p->left, q->left)&& isSameTree(p->right, q->right);
}572. 另一棵树的子树
难度简单
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:

输入:root = [3,4,5,1,2], subRoot = [4,1,2]
输出:true
示例 2:

输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出:false
提示:
root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-10^4 <= root.val <= 10^4
-10^4 <= subRoot.val <= 10^4
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {}解析代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{if (p == NULL && q == NULL){return true;}if (p == NULL || q == NULL)//其中一个为空,另一个不为空{return false;}if (p->val != q->val){return false;}return isSameTree(p->left, q->left)&& isSameTree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {if (root == NULL){return false;}if (isSameTree(root, subRoot)){return true;}//不一样就递归遍历这棵树return isSubtree(root->left, subRoot)|| isSubtree(root->right, subRoot);//只要有一个root返回true就行
}相关文章:

比特数据结构与算法(第四章_下)二叉树OJ(力扣:144,965,104,226,100,572)
144. 二叉树的前序遍历难度简单给你二叉树的根节点 root ,返回它节点值的 前序 遍历。示例 1:输入:root [1,null,2,3]输出:[1,2,3]示例 2:输入:root [ ]输出:[ ]示例 3:输入&#…...

【C++】inline 内联函数
文章目录📕 概念📕 使用前的准备📕 使用📕 特性📕 概念 在 C 中,为了解决一些频繁调用的小函数大量消耗栈空间(栈内存)的问题,特别的引入了 inline 修饰符,表…...
如何审计一个智能合约
智能合约审计用于整个 DeFi 生态系统,通过对协议代码的深入审查,可以帮助解决识别错误、低效代码以及这些问题。智能合约具有不可篡改的特点,这使得审计成为任何区块链项目安全流程的关键部分。 代码审计对任何应用程序都很重要,…...
不用PS,也能实现抠图的工具
对于非设计专业的同学来说,专门下载 PS 抠图有点大材小用,而且运用 PS 对电脑配置一定要求。不过现在有了更多选择,市面上出现了越来越多的抠图软件,不过越多的抠图软件选择也意味着需要花费时间试错因此本文将给大家推荐 3 款非常…...

集群化存储的概述
集群化存储的概述 1、存储的分类方式: 存储的分类-网络拓扑 用于存储的网络拓扑 NAS:小米路由器;SAN:存储区网络–>网络网和存储网络区分开DAS:常见的存储;本地存储 存储分类-存储技术网络拓扑存储技…...
)
asyncio 并发编程(一)
Python2 时代高性能的网络编程主要是 Twisted、Tornado 和 Gevent 这三个库,但是它们的异步代码相互之间既不兼容也不能移植。Gvanrossum 希望在 Python 3 实现一个原生的基于生成器的协程库,其中直接内置了对异步 IO 的支持,这就是 asyncio&…...
:BFC 盒子面试题总结)
春招冲刺(二):BFC 盒子面试题总结
BFC 盒子面试题总结 Q1:BFC盒子是什么? BFC全称是Block Formatting Context 意思就是块级格式化上下文。 可以把BFC看做一个容器,容器里边的元素不会影响到容器外部的元素。 Q2:如何创建BFC? 根元素:bo…...
Ep_计网面试题-本地IP地址怎么一层层向上转换?
将数据加上报头打包在一起形成新的数据包继续往下一层传递。拆包的时候就是把数据包去掉包头作为新数据传给上一层 视频讲解: https://edu.csdn.net/course/detail/38090 点我进入 面试宝典 很多人不知道面试问什么,或者其他的XXGuide,那里边的太多没用的,也没有源码解析,都…...
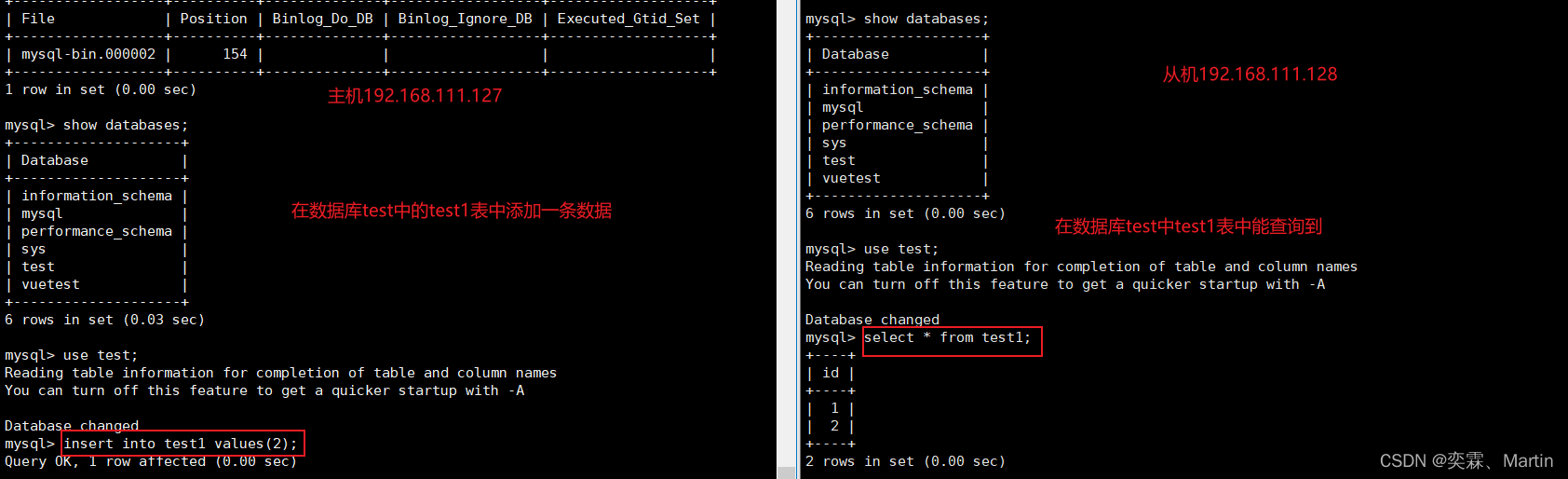
MySQL高级三
目录 三、MySQL高级03 3.1 MyCat 3.1.1 MyCat简介 3.1.2 中间件的作用 3.2 安装MyCat 3.3 主从复制 3.3.1 主从复制的原理 3.3.2 主从复制的好处 3.3.3 配置主从复制 三、MySQL高级03 如果虚拟机的磁盘已满,可以对磁盘进行重新分配 参考:虚拟…...
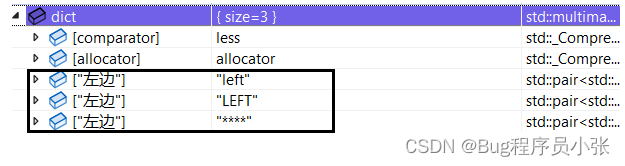
set和map的基本使用
目录 关联式容器 要点分析 键值对 pair介绍 set 模板参数列表: set的构造: 常用接口 操作 multiset map map的构造 插入 make_pair map的迭代器 operator[] multimap multimap中为什么没有重载operator[] 关联式容器 关联式容器也是用…...

已解决pip install wxPython模块安装失败
已解决(pip install wxPython安装失败)error: legacy-instal1-failure Encountered error while trying to install package.wxPython note: This is an issue with the package mentioned above,not pip. hint : See above for output from …...
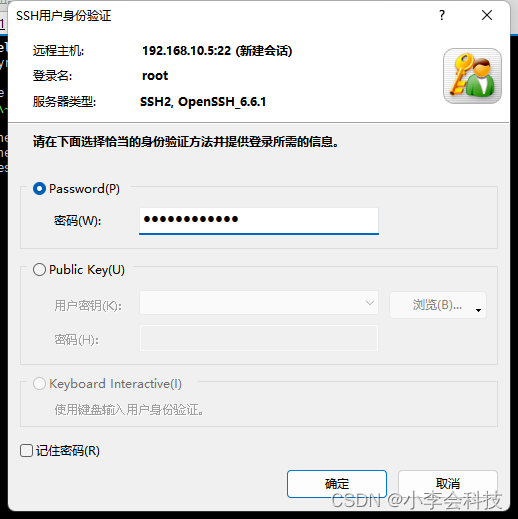
Linux基础——连接Xshell7
个人简介:云计算网络运维专业人员,了解运维知识,掌握TCP/IP协议,每天分享网络运维知识与技能。座右铭:海不辞水,故能成其大;山不辞石,故能成其高。个人主页:小李会科技的…...

C++——智能指针1
目录 RAII auto_ptr模拟实现 智能指针拷贝问题 唯一指针 shared_ptr(可以拷贝) shared_ptr模拟实现 完整代码 循环引用 weak_ptr模拟实现 定制删除器 shared_ptr定制删除器模拟实现 内存泄漏 RAII RAII(Resource Acquisit…...

[数据集][VOC][目标检测]翻越栏杆翻越防护栏数据集目标检测可用yolo训练-1035张介绍
数据集格式:Pascal VOC格式(不包含分割路径的txt文件和yolo格式的txt文件,仅仅包含jpg图片和对应的xml) 图片数量(jpg文件个数):1035 标注数量(xml文件个数):1035 标注类别数:2 标注类别名称:["fylg","…...

深度学习 | BN层原理浅谈
深度学习 | BN层原理浅谈 文章目录深度学习 | BN层原理浅谈一. 背景二. BN层作用三. 计算原理四. 注意事项为什么BN层一般用在线性层和卷积层的后面,而不是放在激活函数后为什么BN能抑制过拟合(有争议)一. 背景 神经网络在训练时,由于内存限制࿰…...

每日面试题
2022/12/15 如何实现一个IOC容器 1、配置文件配置包扫描路径 2、递归包扫描获取.class文件 3、反射、确定需要交给lOC管理的类4、对需要注入的类进行依赖注入 配置文件中指定需要扫描的包路径 定义一些注解,分别表示访问控制层、业务服务层、数据持久层、依赖注…...
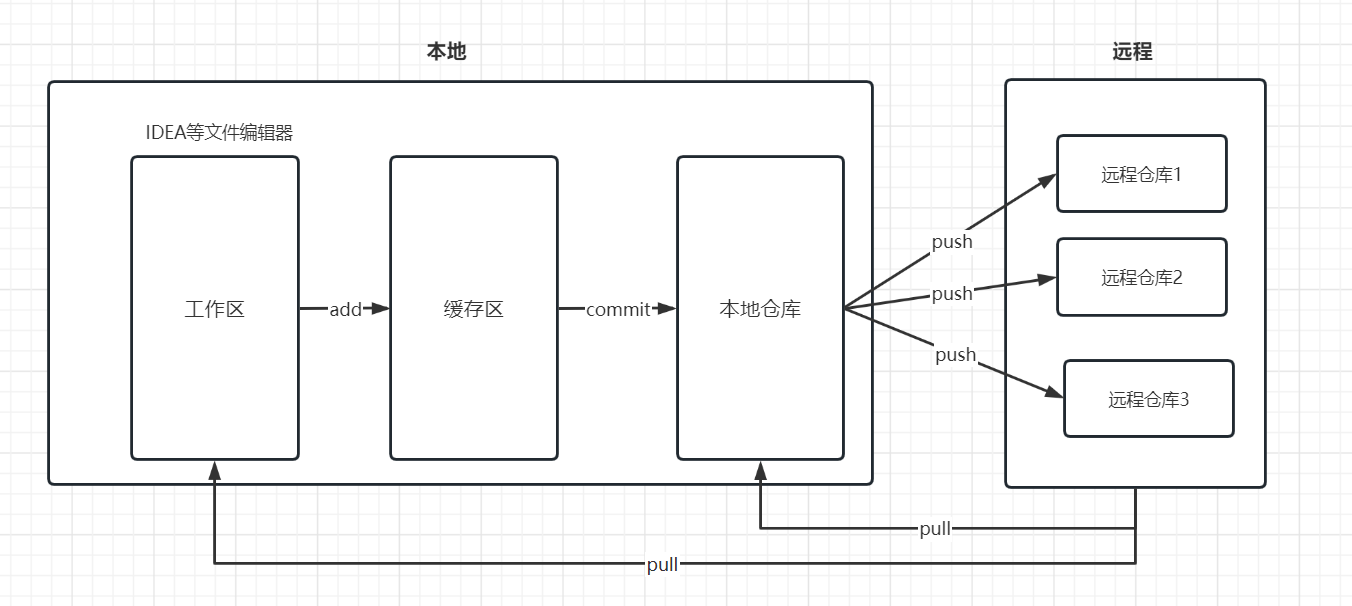
将IDEA的项目托管到gitee
目录1. 在gitee上创建仓库2. 本地创建仓库目录3. 将项目添加到缓冲区4. 将缓冲区的项目添加到本地仓库5. 将本地仓库的项目上传到gitee6. 遇到的问题6.1 问题描述6.2 解决方法7. 相关图示与补充8. 相关参考1. 在gitee上创建仓库 2. 本地创建仓库目录 在IDEA中选择创建 Git 仓…...

父类子类静态代码块、构造代码块、构造方法执行顺序
github:https://github.com/nocoders/java-everything.git 名词解释 静态代码块:java中使用static关键字修饰的代码块,每个代码块只会执行一次,JVM加载类时会执行静态代码块中的代码,静态代码块先于主方法执行。构造代码块&#…...
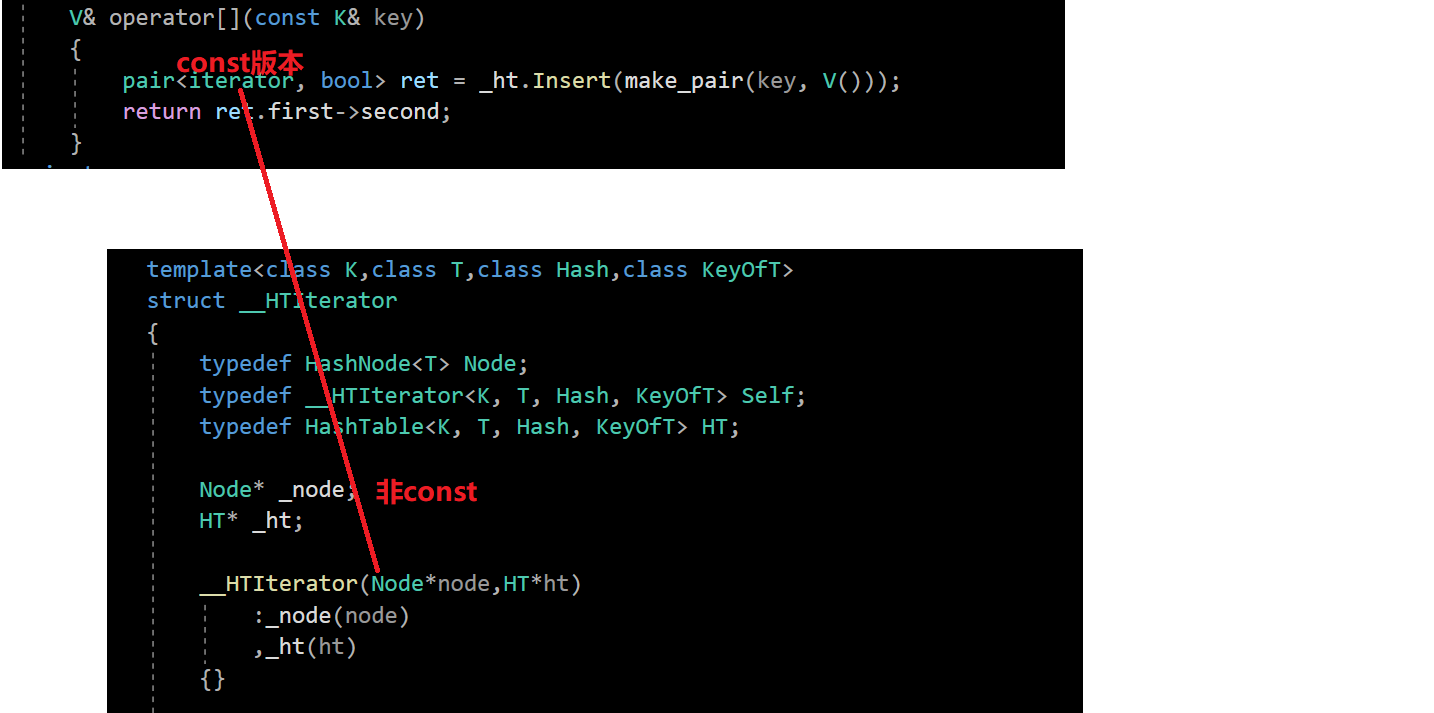
【C++】开散列实现unordered_map与unordered_set的封装
本文主要介绍unordered_map与unordered_set的封装,此次封装主要用上文所说到的开散列,通过开散列的一些改造来实现unordered_map与unordered_set的封装 文章目录一、模板参数二、string的特化三、正向迭代器四、构造与析构五、[]的实现六、unordered_map的实现七、u…...
)
华为OD机试真题Python实现【删除指定目录】真题+解题思路+代码(20222023)
删除指定目录 题目 某文件系统中有 N 个目录, 每个目录都一个独一无二的 ID。 每个目录只有一个付目录, 但每个目录下可以有零个或多个子目录, 目录结构呈树状结构。 假设 根目录的 ID 为0,且根目录没有父目录 ID 用唯一的正整数表示,并统一编号 现给定目录 ID 和其付目…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...
