【华为OD题库-064】最小传输时延I-java
题目
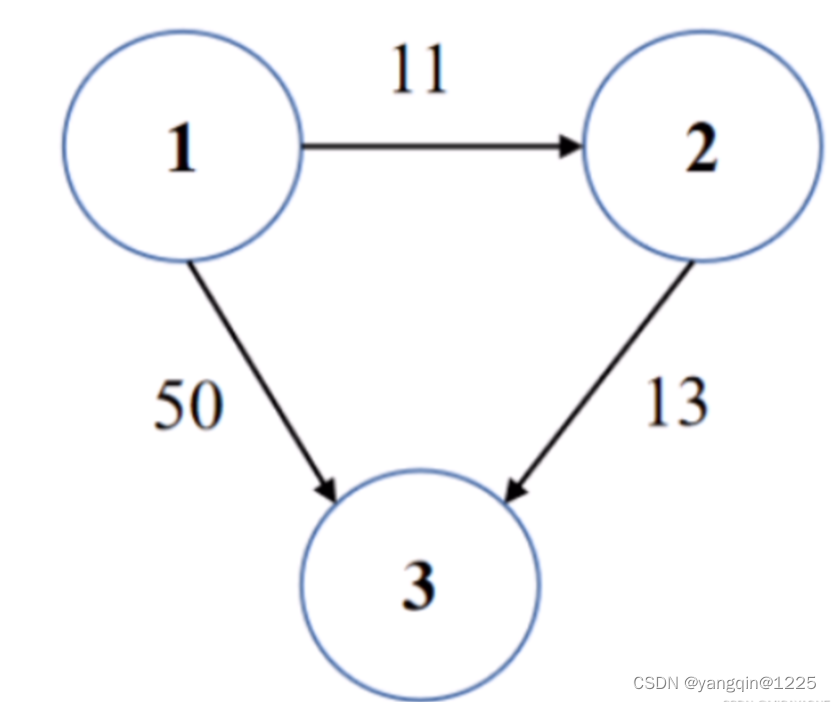
某通信网络中有N个网络结点,用1到N进行标识。网络通过一个有向无环图.表示,其中图的边的值表示结点之间的消息传递时延。
现给定相连节点之间的时延列表times[]={u,v, w),其中u表示源结点,v表示目的结点,w表示u和v之间的消息传递的时延。请计算给定源结点到目的结点的最小传输时延,如果目的结点不可达,返回-1。
注:N的取值范围为[1,100];
时延列表times的长度不超过6000,且1<= u,v<= N,0<=w <= 100;
输入描述:
输入的第一行为两个正整数,分别表示网络结点的个数N,以及时延列表的长度M,用空格分隔;
接下来的M行为两个结点间的时延列表[u v w];
输入的最后一行为两个正整数,分别表示源结点和目的结点。
输出描述:
起点到终点得最小时延,不可达则返回-1
示例1:
输入:
3 3
1 2 11
2 3 13
1 3 50
1 3
输出:
24
思路
Dijkstra 算法,该算法B站视频讲解得较清楚
同leetcode: 743. 网络延迟时间
每次从未标记的节点中选择距离起点最近的节点,标记
计算刚加入节点A的邻近节点B的距离(不包含标记的节点),若(节点A的距离+节点A到节点B的边长)<节点B的距离,就更新节点B的距离
题解
package hwod;import java.util.Arrays;
import java.util.Scanner;public class TheLeastDelayTime {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt(), m = sc.nextInt();int[][] nums = new int[m][3];for (int i = 0; i < m; i++) {for (int j = 0; j < 3; j++) {nums[i][j] = sc.nextInt();}}int start = sc.nextInt(), end = sc.nextInt();System.out.println(theLeastDelayTime(nums, n, start, end));}private static int theLeastDelayTime(int[][] nums, int n, int start, int end) {int[][] g = new int[n][n];final int INF = Integer.MAX_VALUE / 2;//防止越界//g[i][j]代表节点i到节点j的距离for (int i = 0; i < n; i++) {Arrays.fill(g[i], INF);}for (int[] t : nums) {int x = t[0] - 1, y = t[1] - 1;g[x][y] = t[2];}int[] used = new int[n];//判断某个节点是否被标记int[] dist = new int[n];//每个节点到起点的距离Arrays.fill(dist, INF);dist[start - 1] = 0;for (int i = 0; i < n; i++) {//每次更新一个distint x = -1;//找到未标记的,距离起点最近的节点xfor (int y = 0; y < n; y++) {if (used[y] == 0 && (x == -1 || dist[y] < dist[x])) {x = y;}}used[x] = 1;//更新标记节点邻近的节点距离for (int y = 0; y < n; y++) {dist[y] = Math.min(dist[y], dist[x] + g[x][y]);}}return dist[end - 1] == INF ? -1 : dist[end - 1];}
}推荐
如果你对本系列的其他题目感兴趣,可以参考华为OD机试真题及题解(JAVA),查看当前专栏更新的所有题目。
相关文章:
【华为OD题库-064】最小传输时延I-java
题目 某通信网络中有N个网络结点,用1到N进行标识。网络通过一个有向无环图.表示,其中图的边的值表示结点之间的消息传递时延。 现给定相连节点之间的时延列表times[]{u,v, w),其中u表示源结点,v表示目的结点࿰…...
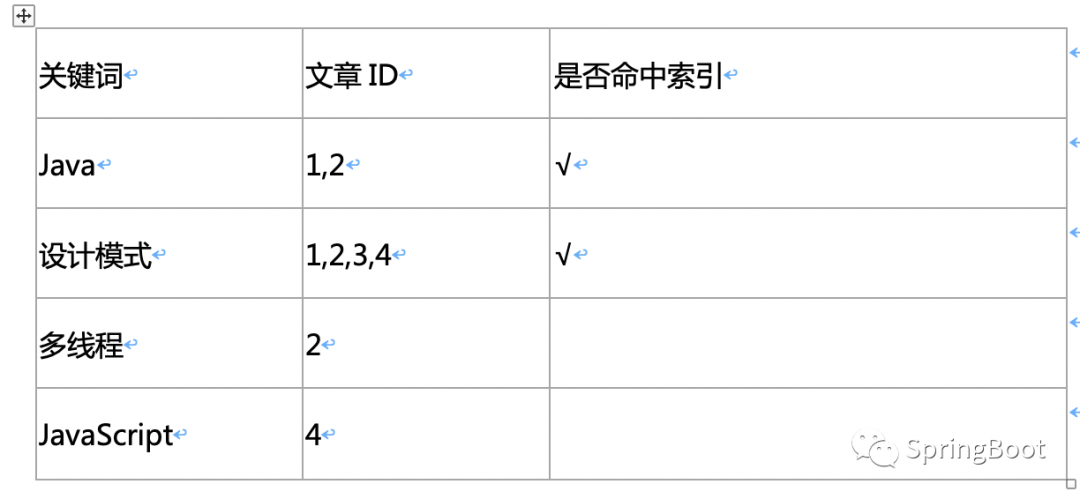
全文检索[ES系列] - 第495篇
历史文章(文章累计490) 《国内最全的Spring Boot系列之一》 《国内最全的Spring Boot系列之二》 《国内最全的Spring Boot系列之三》 《国内最全的Spring Boot系列之四》 《国内最全的Spring Boot系列之五》 《国内最全的Spring Boot系列之六》 M…...

【预计IEEE出版|EI征稿通知】第六届下一代数据驱动网络国际学术会议 (NGDN 2024)
第六届下一代数据驱动网络国际学术会议 (NGDN 2024) The Sixth International Conference on Next Generation Data-driven Networks 2024年4月26-28日 | 中国沈阳 基于前几届在英国埃克塞特 (ISPA 2020) 、中国沈阳 (TrustCom 2021) 和中国武汉 (IEEETrustCom-2022) 成功举…...

C++软件在Win平台运行总结
Windows平台: 1.需要安装运行库:无论是exe还是动态库用的哪种平台工具集(visual2010-visual2019)进行编译,需要安装对应的运行时库vc_redist.x64.exe/vc_redist.x86.exe。比如Exe用的是VisualStdio2010工具集编译,其中链接的一个…...
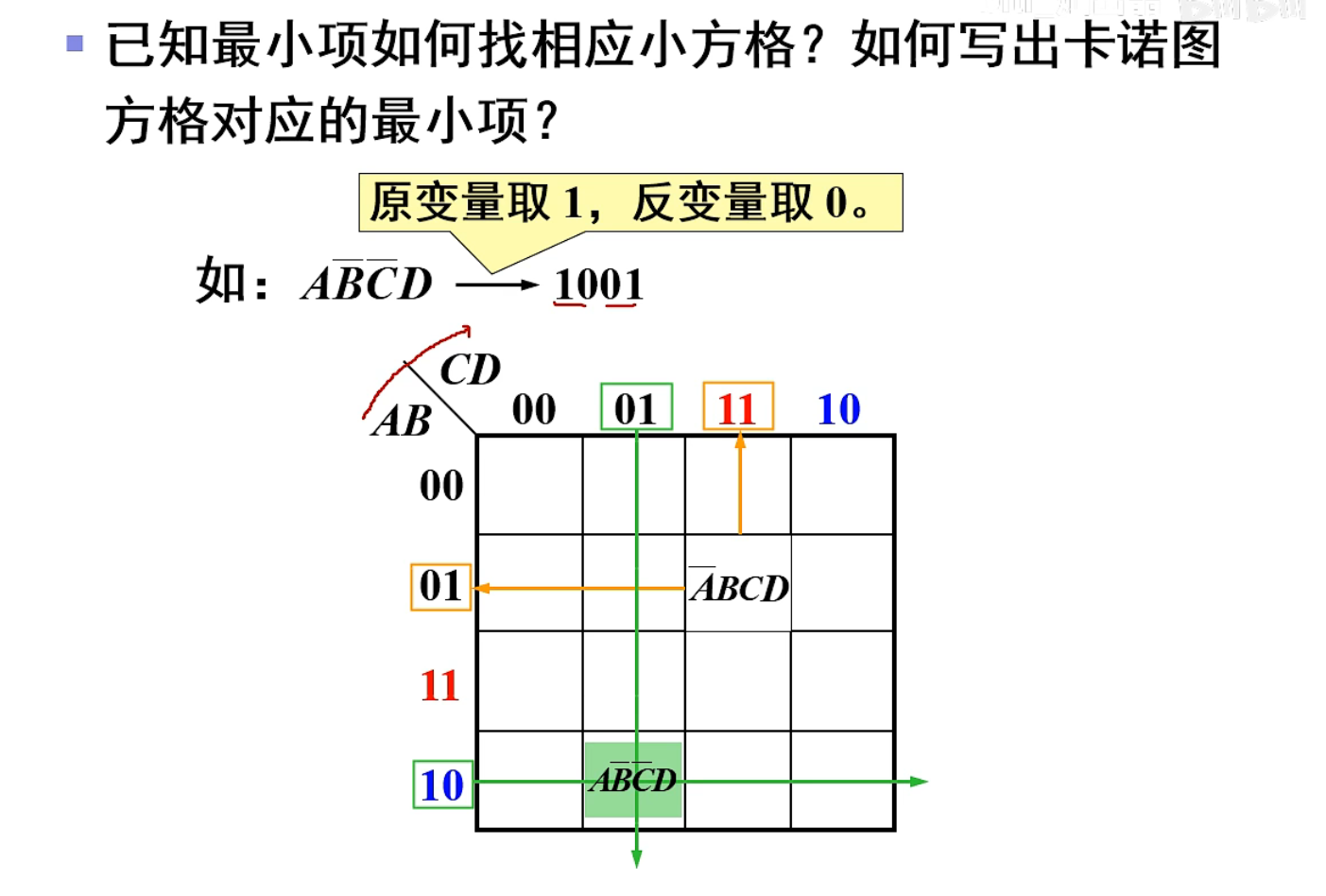
【数电笔记】16-卡诺图绘制(逻辑函数的卡诺图化简)
目录 说明: 最小项卡诺图的组成 1. 相邻最小项 2. 卡诺图的组成 2.1 二变量卡诺图 2.2 三表变量卡诺图 2.3 四变量卡诺图 3. 卡诺图中的相邻项(几何相邻) 说明: 笔记配套视频来源:B站;本系列笔记并…...
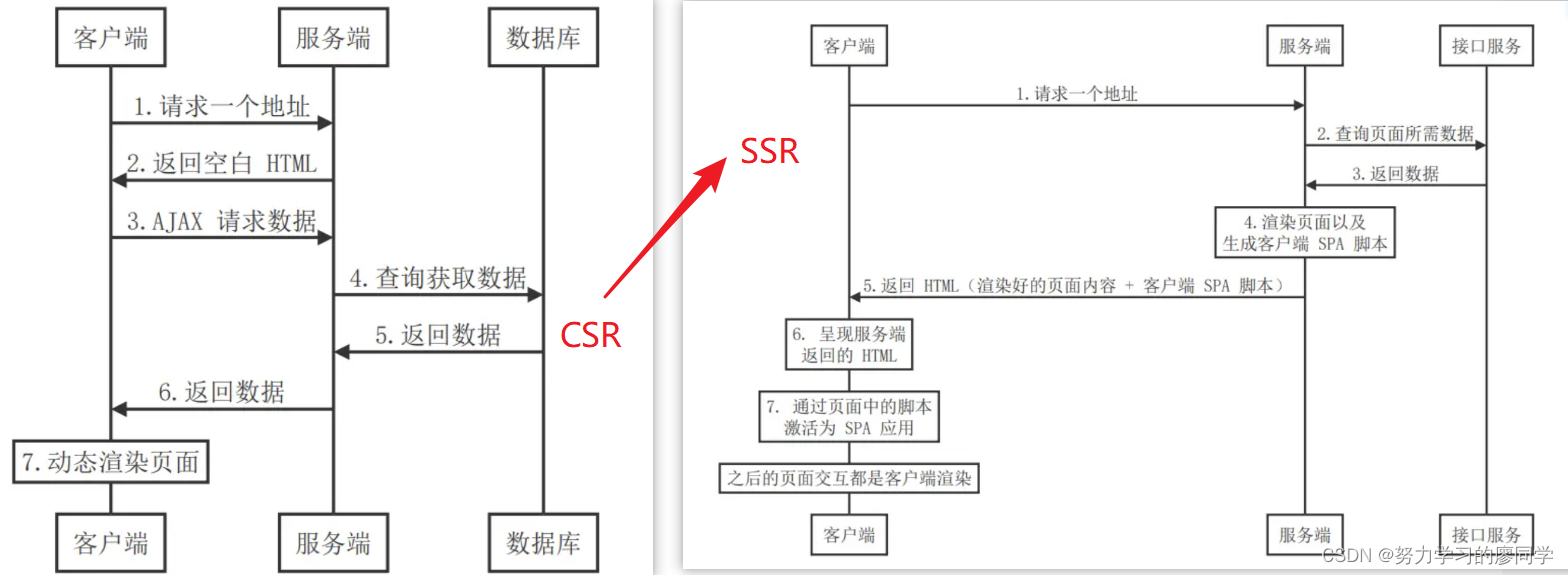
前端面试灵魂提问(1)
1.自我介绍 2.在实习中,你负责那一模块 3.any与unknow的异同 相同点:any和unkonwn 可以接受任何值 不同点:any会丢掉类型限制,可以用any 类型的变量随意做任何事情。unknown 变量会强制执行类型检查,所以在使用一个…...
Linux中项目部署步骤
安装jdk,tomcat 安装步骤 1,将压缩包,拷贝到虚拟机中。 通过工具,将文件直接拖到虚拟机的/home下 2,回到虚拟机中,查看/home下,有两个压缩文件 3,给压缩文件做解压缩操作 tar -z…...

cmd下查看python命令的用法
在cmd下,可以运行python --help或者py --help来查看python命令的用法。例如:...
)
大型语言模型在实体关系提取中的应用探索(二)
上一篇文章我们探讨了如何使用大语言模型进行实体关系的抽取。本篇文章我们将进一步探索这个话题。比较一下国内外几款知名大模型在相同的实体关系提取任务下的表现。由于精力有限,我们无法全面测试各模型的实体关系抽取能力,因此,看到的效果…...

Easy Excel设置表格样式
1. 设置通用样式 import com.alibaba.excel.annotation.ExcelProperty; import com.alibaba.excel.annotation.write.style.*; import com.fasterxml.jackson.annotation.JsonFormat; import com.xxx.npi.config.easypoi.EasyExcelDateConverter; import lombok.Data; import …...
HarmonyOS/OpenHarmony应用开发
OpenHarmony是由开放原子开源基金会(OpenAtom Foundation)孵化及运营的开源项目, 目标是面向全场景、全连接、全智能时代, 搭建一个智能终端设备操作系统的框架和平台, 促进万物互联产业的繁荣发展。 了解OpenHarmony HarmonyOS是华为通过OpenHarmony项目,结合商业…...
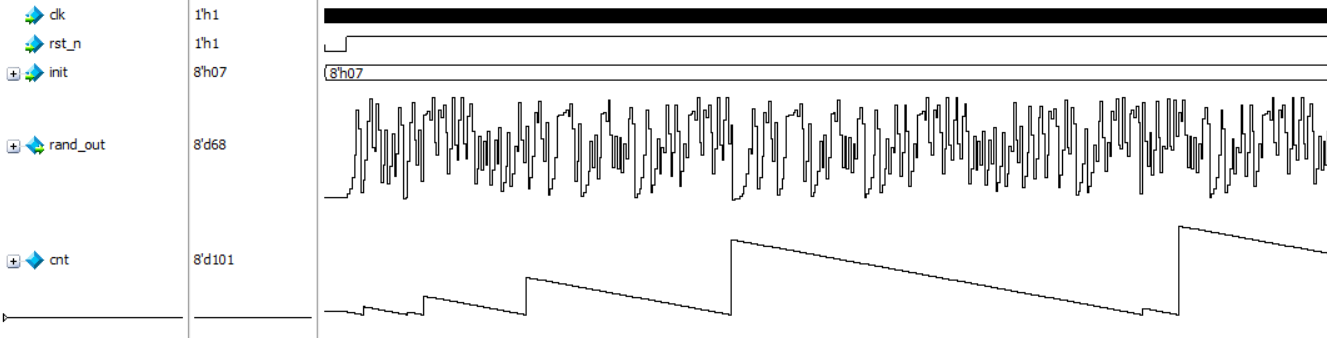
孩子都能学会的FPGA:第二十一课——用线性反馈移位寄存器实现伪随机序列
(原创声明:该文是作者的原创,面向对象是FPGA入门者,后续会有进阶的高级教程。宗旨是让每个想做FPGA的人轻松入门,作者不光让大家知其然,还要让大家知其所以然!每个工程作者都搭建了全自动化的仿…...

国内 AI 成图第一案!你来你会怎么判?
我国目前并未出台专门针对网络爬虫技术的法律规范,但在司法实践中,相关判决已屡见不鲜,K 哥特设了“K哥爬虫普法”专栏,本栏目通过对真实案例的分析,旨在提高广大爬虫工程师的法律意识,知晓如何合法合规利用…...

快速登录界面关于如何登录以及多账号列表解析以及config配置文件是如何读取(1)
快速登录界面关于如何登录以及多账号列表解析以及config配置文件是如何读取 1、快速登录界面关于如何登录以及快速登录界面账号如何显示 如图所示:根据按下按钮一键登录中途会发生什么。 关于一键登录按钮皮肤skin的设置: <Button name"QuickLoginOkBtn" text&q…...
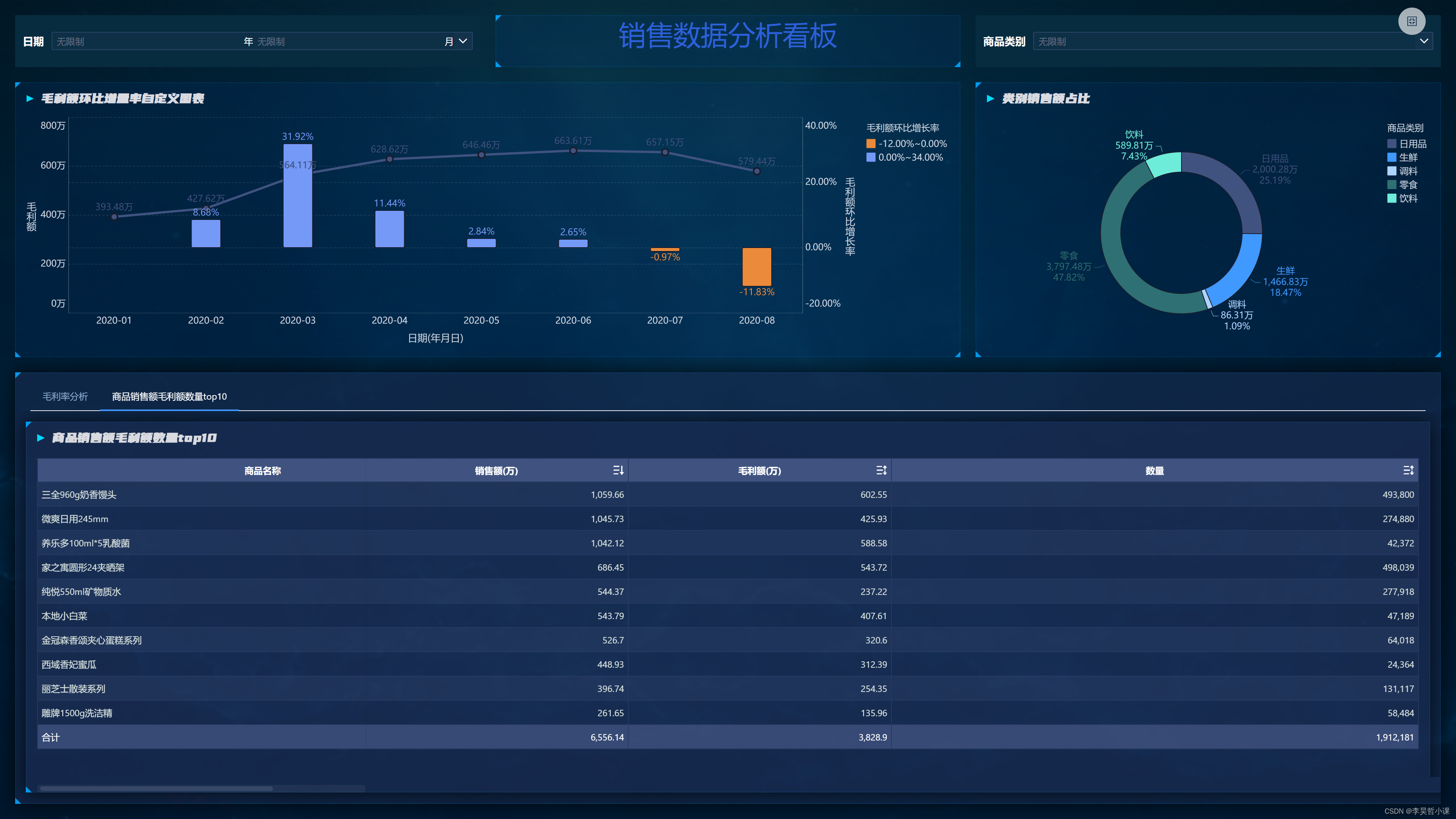
finebi 新手入门案例
finebi 新手入门案例 连锁超市销售数据分析 步骤: 准备公共数据新建分析主题处理数据在数据中分析在图形中分析数据大屏 准备公共数据 点击公共数据 点击新建文件夹 修改文件夹名称 上传数据 鼠标悬停在文件夹上,右侧出现 鼠标悬停在文件夹上&#x…...
)
1. 小游戏(贪心)
题干: 谷同学很喜欢玩计算机游戏,特别是战略游戏,但是有时他不能尽快找到解所以常常感到很沮丧。现在面临如下问题:他必须在一个中世纪的城堡里设防,城堡里的道路形成一棵无向树。要在结点上安排最少的士兵使得他们可以…...

记录 | c++打印变量类型
c打印变量类型: 使用 typeid(变量名).name() int main(){std::cout << "type of ss : " << typeid(ss).name() << std::endl; }...
nodejs_vue+vscode美容理发店会员管理系统un1dm
按照设计开发一个系统的常用流程来描述系统,可以把系统分成分析阶段,设计阶段,实现阶段,测试阶段。所以在编写系统的说明文档时,根据系统所处的阶段来描述系统的内容。 绪论:这是对选题的背景,意…...
C语言 操作符详解
C语言学习 目录 文章目录 前言 一、算术操作符 二、移位操作符 2.1 左移操作符 2.2 右移操作符 三、位操作符 3.1 按位与操作符 & 3.2 按位或操作符 | 3.3 按位异或操作符 ^ 四、赋值操作符 五、单目操作符 5.1 逻辑反操作符! 5.2 正值、负值-操作符 5.3 取地址…...
成为AI产品经理——回归模型评估(MSE、RMSE、MAE、R方)
分类问题的评估是看实际类别和预测类别是否一致,它的评估指标主要有混淆矩阵、AUC、KS。回归问题的评估是看实际值和预测值是否一致,它的评估指标包括MAE、MSE、RMSE、R方。 如果我们预测第二天某支股票的价格,给一个模型 y1.5x,…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...
