Leetcode.2477 到达首都的最少油耗
题目链接
Leetcode.2477 到达首都的最少油耗
rating : 2012
题目描述
给你一棵 n n n 个节点的树(一个无向、连通、无环图),每个节点表示一个城市,编号从 0 0 0 到 n − 1 n - 1 n−1 ,且恰好有 n − 1 n - 1 n−1 条路。 0 0 0 是首都。给你一个二维整数数组 r o a d s roads roads ,其中 r o a d s [ i ] = [ a i , b i ] roads[i] = [a_i, b_i] roads[i]=[ai,bi] ,表示城市 a i a_i ai 和 b i b_i bi 之间有一条 双向路 。
每个城市里有一个代表,他们都要去首都参加一个会议。
每座城市里有一辆车。给你一个整数 s e a t s seats seats 表示每辆车里面座位的数目。
城市里的代表可以选择乘坐所在城市的车,或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。
请你返回到达首都最少需要多少升汽油。
示例 1:
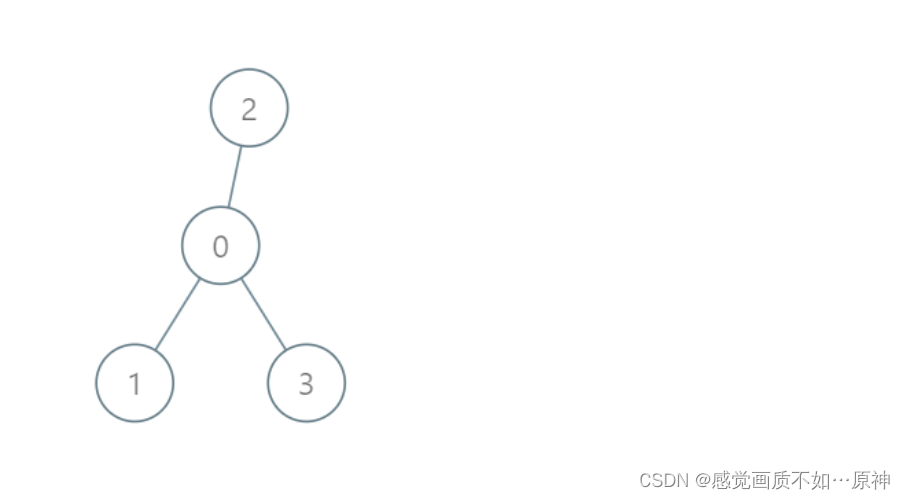
输入:roads = [[0,1],[0,2],[0,3]], seats = 5
输出:3
解释:
- 代表 1 直接到达首都,消耗 1 升汽油。
- 代表 2 直接到达首都,消耗 1 升汽油。
- 代表 3 直接到达首都,消耗 1 升汽油。 最少消耗 3 升汽油。
示例 2:
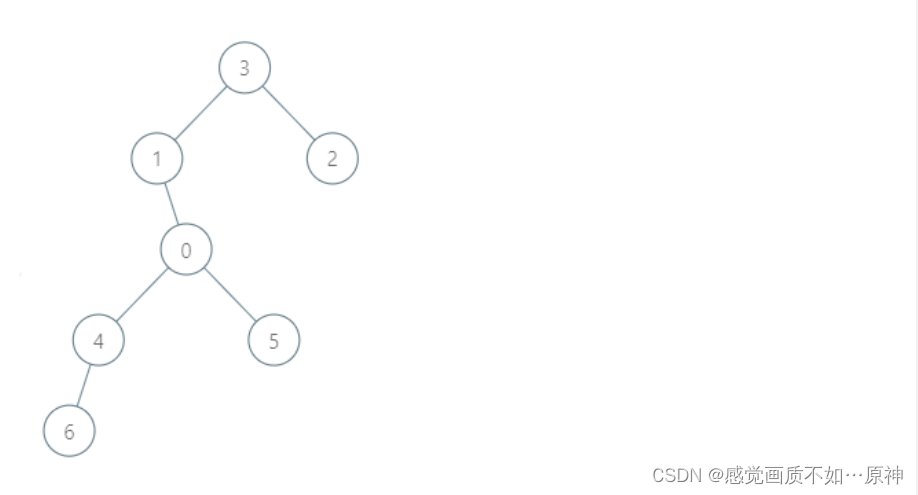
输入:roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
输出:7
解释:
- 代表 2 到达城市 3 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到达城市 1 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到达首都,消耗 1 升汽油。
- 代表 1 直接到达首都,消耗 1 升汽油。
- 代表 5 直接到达首都,消耗 1 升汽油。
- 代表 6 到达城市 4 ,消耗 1 升汽油。
- 代表 4 和代表 6 一起到达首都,消耗 1 升汽油。 最少消耗 7 升汽油。
示例 3:

输入:roads = [], seats = 1
输出:0
解释:没有代表需要从别的城市到达首都。
提示:
- 1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105
- r o a d s . l e n g t h = n − 1 roads.length = n - 1 roads.length=n−1
- r o a d s [ i ] . l e n g t h = 2 roads[i].length = 2 roads[i].length=2
- 0 ≤ a i , b i < n 0 \leq a_i, b_i < n 0≤ai,bi<n
- a i ≠ b i a_i \neq b_i ai=bi
- r o a d s roads roads 表示一棵合法的树。
- 1 ≤ s e a t s ≤ 1 0 5 1 \leq seats \leq 10^5 1≤seats≤105
解法:dfs + 贪心
越靠近起点 0 0 0 的边,经过的车越多,所消耗的燃料也就越多。
由于我们求得是消耗的最少的燃料,假设以点 v v v 为根节点的子树上的所有节点都要经过边 { u , v } \{ u,v\} {u,v} 到点 u u u,子树 v v v 的节点总数为 c n t v cnt_v cntv,那么要让 c n t v cnt_v cntv 个节点都被移动到 点 u u u ,最少需要 ⌈ c n t v s e a t s ⌉ \lceil \frac{cnt_v}{seats} \rceil ⌈seatscntv⌉ 辆车,为了用尽可能少的燃料,所以我们直接用 ⌈ c n t v s e a t s ⌉ \lceil \frac{cnt_v}{seats} \rceil ⌈seatscntv⌉ 辆车。
那么对于 边 { u , v } \{ u,v\} {u,v},一共有 ⌈ c n t v s e a t s ⌉ \lceil \frac{cnt_v}{seats} \rceil ⌈seatscntv⌉ 辆车通过了这条边,所以一共要消耗 ⌈ c n t v s e a t s ⌉ \lceil \frac{cnt_v}{seats} \rceil ⌈seatscntv⌉ 升燃料。
我们直接从 起点 0 0 0 开始遍历所有的边,记录总的燃料即可。
时间复杂度 : O ( n ) O(n) O(n)
C++代码:
using LL = long long;class Solution {
public:long long minimumFuelCost(vector<vector<int>>& roads, int seats) {unordered_map<int,vector<int>> g;int n = 0;for(auto &e:roads){int a = e[0] , b = e[1];n = max({a,b,n});g[a].push_back(b);g[b].push_back(a);}n++;//s[i] 就是以 i 为根节点的节点总数vector<int> s(n);LL ans = 0;function<int(int,int)> dfs = [&](int u,int fa) ->int{s[u] = 1;for(auto v:g[u]){if(v == fa) continue;s[u] += dfs(v,u);}//不统计根节点if(u != 0) ans += (s[u] + seats - 1) / seats;return s[u];};dfs(0,-1);return ans;}
};
相关文章:

Leetcode.2477 到达首都的最少油耗
题目链接 Leetcode.2477 到达首都的最少油耗 rating : 2012 题目描述 给你一棵 n n n 个节点的树(一个无向、连通、无环图),每个节点表示一个城市,编号从 0 0 0 到 n − 1 n - 1 n−1 ,且恰好有 n − 1 n - 1 n−…...
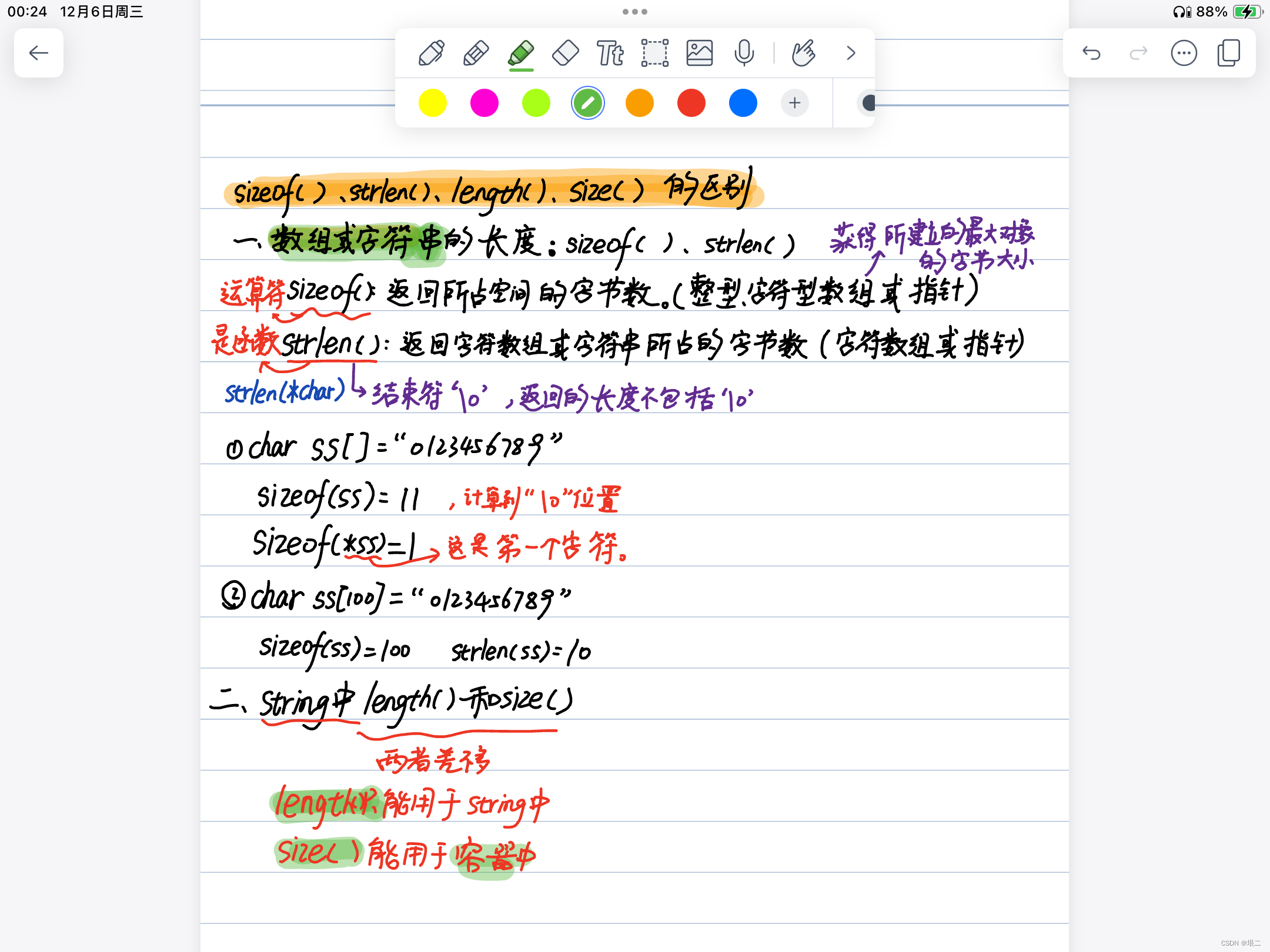
sizeof()、strlen()、length()、size()的区别(笔记)
上面的笔记有点简陋,可以看一下下面这个博主的: c/c中sizeof()、strlen()、length()、size()详解和区别_csize,sizeof,length_xuechanba的博客-CSDN博客...
)
Redis击穿(热点key失效)
Redis击穿是指在高并发情况下,一个键在缓存中过期失效时,同时有大量请求访问该键,导致所有请求都落到数据库上,对数据库造成压力。这种情况下,数据库可能无法及时处理这些请求,导致性能下降甚至崩溃。 为了…...

分类预测 | Matlab实现OOA-CNN-SVM鱼鹰算法优化卷积支持向量机分类预测
分类预测 | Matlab实现OOA-CNN-SVM鱼鹰算法优化卷积支持向量机分类预测 目录 分类预测 | Matlab实现OOA-CNN-SVM鱼鹰算法优化卷积支持向量机分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现OOA-CNN-SVM鱼鹰算法优化卷积支持向量机分类预测࿰…...
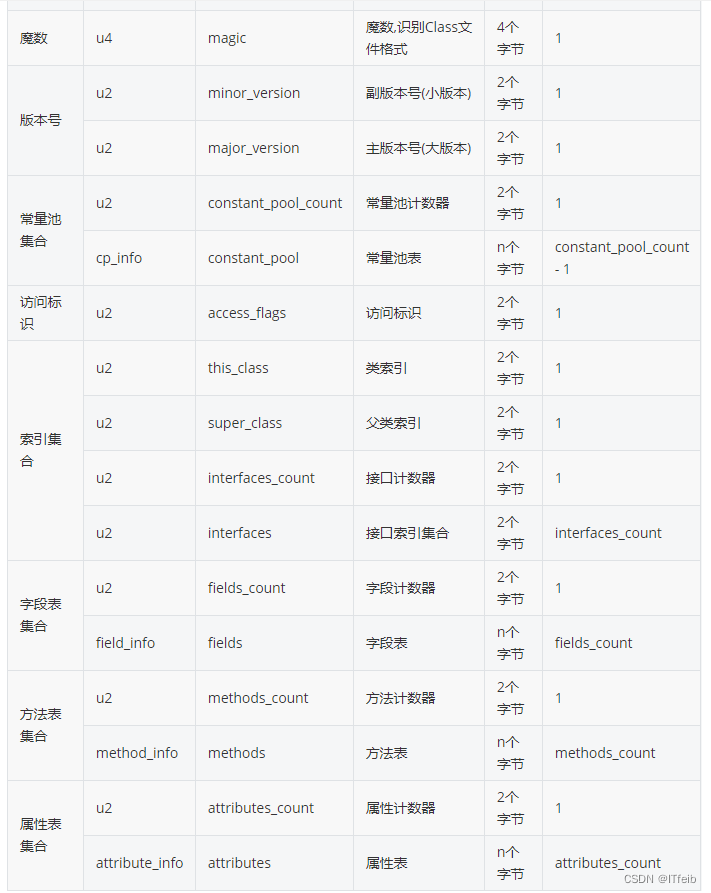
class文件结构
文章目录 1. 常量池集合2. 访问标志3. 字段表集合4. 方法表集合5. 属性表集合 成员变量(非静态)的赋值过程:1. 默认初始化 2. 显示初始化/代码块中初始化 3. 构造器中初始化 4. 有了对象后对象。属性或者对象。方法的方式对成员变量进行赋值 …...

多重背包问题 一句话说清楚“二进制拆分“
目录 区别: 一句话说清楚: 板子: 区别: 得先懂完全背包问题完全背包问题 非零基础-CSDN博客 都是让背包内价值最大。 完全背包问题每种物品可以取无数次。而多重背包问题每件取的次数有限。 都可以用的最挫的方法就是0~k件去…...

nodejs微信小程序+python+PHP本科生优秀作业交流网站的设计与实现-计算机毕业设计推荐
通过软件的需求分析已经获得了系统的基本功能需求,根据需求,将本科生优秀作业交流网站功能模块主要分为管理员模块。管理员添加系统首页、个人中心、用户管理、作业分类管理、作业分享管理、论坛交流、投诉举报、系统管理等操作。 随着信息化社会的形成…...

使用git出现的问题
保证 首先保证自己的git已经下载 其次保证自己的gitee账号已经安装并且已经生成ssh公钥 保证自己要push的代码在要上传的文件夹内并且配置文件等都在父文件夹(也就是文件没有套着文件) 问题 1 $ git push origin master gitgitee.com: Permission de…...
)
rk3568 适配PCIE(二)
rk3568 适配pcie3.0 PCIe(Peripheral Component Interconnect Express)是一种用于连接计算机主板和其他设备的高速串行总线接口。PCIe 2.0和PCIe 3.0是两个不同版本的PCIe规范,它们在以下几个方面有所不同: 带宽:PCIe 2.0的理论带宽为每条通道5 Gbps,而PCIe 3.0的理论带…...

Java基础 进制
在Java中,可以使用不同的进制表示整数常量和字面量。 十进制(Decimal):默认为十进制,不需要添加前缀。例如:int num 10;二进制(Binary):以0b或0B作为前缀表示二进制。例…...

springboot中@Builder注解的详细用法实例,跟数据库结合。
在Spring Boot中,Builder注解是Lombok库提供的一个注解,用于生成带有Builder模式支持的构造器方法。通过Builder注解,可以简化对象的创建过程,特别适用于需要设置多个属性的情况。 下面是一个使用Builder注解的示例: …...

WT2605C蓝牙音频语音芯片:具备大功率IO驱动能力,引领音频技术新纪元
在当今的电子科技时代,功率强大的IO驱动能力成为音频设备性能的重要指标。近日,一款名为WT2605C的蓝牙音频语音芯片,以其最高可直接驱动64mA的大功率IO驱动能力,引起业界的广泛关注。这款芯片的出现,无疑将为音频设备的…...

【Java 基础】20 多线程操作方法
文章目录 1.获取和设置线程的名字1)获取默认名字2)获取自定义的名字 2.判断线程是否启动3.线程的强制执行4.让线程睡一会儿5.中断线程6.守护线程7.线程的礼让 前一节我们介绍了线程的定义、创建方法、状态以及各状态间的转换。在状态转换处只是简单的说明…...

SpringBoot使用mybatis-plus分页查询无效解决方案
问题概述 SpringBoot中使用mybatis-plus实现分页查询时,提供一个page分页对象和一个QueryWrapper条件类对象,在使用Service.page(page,queryWrapper)方法进行分页查询时,发现并未查询到分页的结果,反而是查询到全部符合条件的结果…...
)
QT 中 线程池 (备查)
QRunnable类 API 1)在Qt中使用线程池需要先创建任务,添加到线程池中的每一个任务都需要是一个 QRunnable 类型,因此在程序中需要创建子类继承 QRunnable 这个类。 2)然后重写 run() 方法,在这个函数中编写要在线程池中…...

LeetCode刷题笔记第71题:简化路径
LeetCode刷题笔记第71题:简化路径 题目 给定一个路径,简化路径 要求: 1、以’/‘开头 2、两个目录之间只有一个’/’ 3、不能以’/‘结尾 4、路径中不能有’.‘和’…’ 想法 利用栈的数据存储方式的思想,将路径字符顺序入栈遇…...
JavaScript <md5加密的两种不同输出结果分析>--案例(二点一)
前言: 问题是这样的,在浏览器中看到这段代码 然后在控制台进行输出.得到: 紧接着,就在,js文件里面进行转译: 可是,得到的结果是: 这是问题!!! 正题: 为什么相同的js代码,在 .js 文件中的输出与 Chrome 控制台中的输出不一样? 环境差异:不同的JavaScript环境&…...
『亚马逊云科技产品测评』活动征文|基于亚马逊EC2云服务器配置Nginx静态网页
授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre, 知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道 亚马逊EC2云服务器(Elastic Compute Cloud)是亚马…...
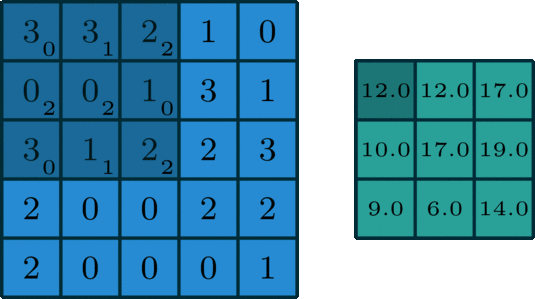
28、卷积 - 卷积的基础公式
本节推导一下卷积的基础公式,还是先上一张卷积运算的示意图图。 我们知道,一张图片有 3 个维度,分别是长、宽、通道。 这三个维度分别用 3 个字母代替,分别是 H(Height, 对应的是长这一维度), W(Width, 对应的是宽这一维度),C(Channel,对应的是通道这一维度)。 对于…...

Mac电脑vm虚拟机 VMware Fusion Pro中文 for mac
VMware Fusion Pro是一款功能强大的虚拟机软件,适用于需要在Mac电脑上运行其他操作系统的用户。它具有广泛的支持、快速稳定的特点以及多种高级功能,可以满足用户的各种需求和场景。 多操作系统支持:VMware Fusion Pro允许在Mac电脑上运行多…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
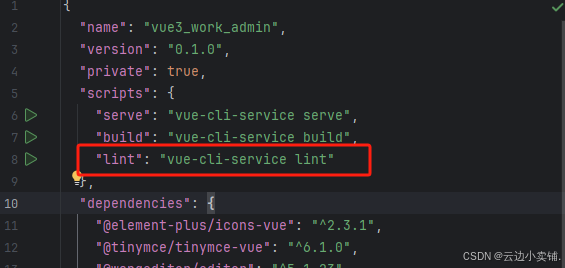
运行vue项目报错 errors and 0 warnings potentially fixable with the `--fix` option.
报错 找到package.json文件 找到这个修改成 "lint": "eslint --fix --ext .js,.vue src" 为elsint有配置结尾换行符,最后运行:npm run lint --fix...

JVM——对象模型:JVM对象的内部机制和存在方式是怎样的?
引入 在Java的编程宇宙中,“Everything is object”是最核心的哲学纲领。当我们写下new Book()这样简单的代码时,JVM正在幕后构建一个复杂而精妙的“数据实体”——对象。这个看似普通的对象,实则是JVM内存管理、类型系统和多态机制的基石。…...

2025年上海市“星光计划”第十一届职业院校技能大赛 网络安全赛项技能操作模块样题
2025年上海市“星光计划”第十一届职业院校技能大赛 网络安全赛项技能操作模块样题 (二)模块 A:安全事件响应、网络安全数据取证、应用安全、系统安全任务一:漏洞扫描与利用:任务二:Windows 操作系统渗透测试 :任务三&…...

2025年ESWA SCI1区TOP,自适应学习粒子群算法AEPSO+动态周期调节灰色模型,深度解析+性能实测
目录 1.摘要2.粒子群算法PSO原理3.改进策略4.结果展示5.参考文献6.代码获取7.算法辅导应用定制读者交流 1.摘要 能源数据的科学预测对于能源行业决策和国家经济发展具有重要意义,尤其是短期能源预测,其精度直接影响经济运行效率。为了更好地提高预测模型…...

MTK-Android12-13 Camera2 设置默认视频画质功能实现
MTK-Android12-13 Camera2 设置默认视频画质功能实现 场景:部分客户使用自己的mipi相机安装到我们主板上,最大分辨率为1280720,但是视频画质默认的是640480。实际场景中,在默认视频分辨率情况下拍出来的视频比较模糊、预览也不清晰…...

c++ decltype关键字
decltype为类型推导关键字。 示例代码: // decltype也可用于函数模板编程: template<typename T, typename U> auto add(T t, U u) -> decltype(t u) {return t u; }// decltype推导函数返回类型 auto doubleNumFunc(int x) -> decltype(x * 2) {ret…...
