《数据结构、算法与应用C++语言描述》-线索二叉树的定义与C++实现
_23Threaded BinaryTree
可编译运行代码见:GIithub::Data-Structures-Algorithms-and-Applications/_24Threaded_BinaryTree
线索二叉树定义
在普通二叉树中,有很多nullptr指针被浪费了,可以将其利用起来。
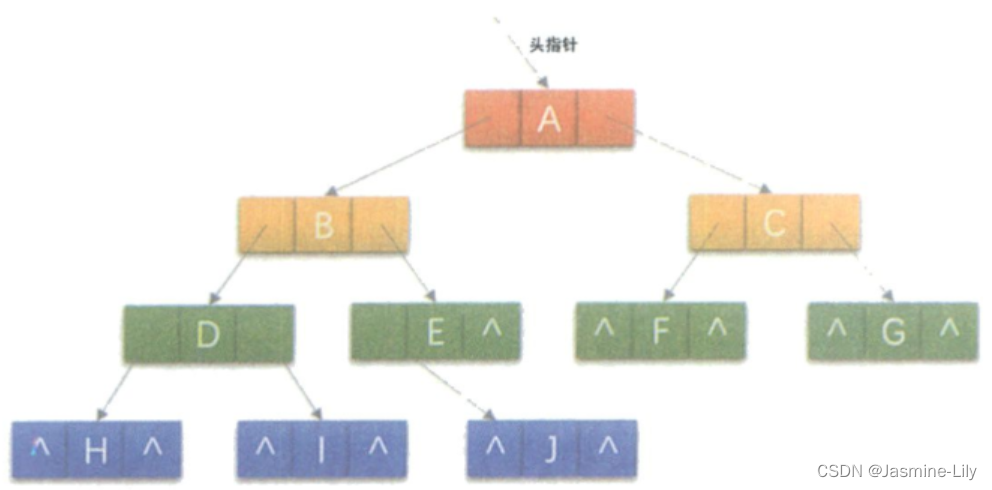
首先我们要来看看这空指针有多少个呢?对于一个有n个结点的二叉链表,每个结点有指向左右孩子的两个指针域,所以一共是2n个指针域。而n个结点的二叉树一共有n-1条分支线数,也就是说,其实是存在2n-(n-1)=n+1个空指针域。
对上图**(参考:《大话数据结构 溢彩加强版 程杰》160页图)**做中序遍历,得到了HDIBJEAFCG这样的字符序列,遍历过后,我们可以知道,结点I的前驱是D,后继是B,结点F的前驱是A,后继是C。也就是说,我们可以很清楚地知道任意一个结点,它的前驱和后继是哪一个结点。
可是这是建立在已经遍历过的基础之上的。在二叉链表上,我们只能知道每个结点指向其左右孩子结点的地址,而不知道某个结点的前驱是谁,后继是谁。要想知道,必须遍历一次。以后每次需要知道时,都必须先遍历一次。这样比较浪费时间。
我们可以考虑利用那些空地址,存放指向结点在某种遍历次序下的前驱和后继结点的地址。我们把这种指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表,相应的二叉树就称为线索二叉树(Threaded Binary Tree)。
我们把二叉树进行中序遍历后,将所有的空指针域中的rchild,改为指向它的后继结点。将所有空指针域中的lchild,改为指向当前结点的前驱。由此得出,经过线索化的二叉树变成了一个双向链表。双向链表相比于二叉树更容易找到某节点的前驱和后继节点。因此,如果所用的二叉树需经常遍历或查找结点时需要某种遍历序列中的前驱和后继,那么采用线索二叉链表的存储结构就是非常不错的选择。
但是还有一个问题,如果将这些空指针作为线索后无法区分该指针是线索还是指向孩子节点,因此需要标志位LTag为True表示该节点的左指针是索引,RLag为true表示该节点的右指针是索引,反之不是索引。
代码
main.cpp
/*
Project name : _24Threaded_BinaryTree
Last modified Date: 2023年11月28日17点06分
Last Version: V1.0
Descriptions: 线索二叉树
*/
#include "inThreadedBinaryTreeChains.h"
int main() {inThreadedBinaryTreeChainsTest();return 0;
}inThreadedBinaryTreeChains.h
/*
Project name : _24Threaded_BinaryTree
Last modified Date: 2023年11月28日17点06分
Last Version: V1.0
Descriptions: 线索二叉树链表表示
*/#ifndef _24THREADED_BINARYTREE_INTHREADEDBINARYTREE_H
#define _24THREADED_BINARYTREE_INTHREADEDBINARYTREE_H
#include <iostream>
#include "binaryTree.h"
#include "inThreadedBinaryTreeNode.h"
using namespace std;
/*二叉树基础测试函数*/
void inThreadedBinaryTreeChainsTest();
template<class E>
class inThreadedBinaryTreeChains : public binaryTree<inThreadedBinaryTreeNode<E>>
{
public:/*二叉树的基础成员函数*//*构造函数函数*/inThreadedBinaryTreeChains() {root = nullptr; treeSize = 0;}/*析构函数*/~inThreadedBinaryTreeChains() { erase(); }/*当树为空时,返回true;否则,返回false*/bool empty() const { return treeSize == 0; }/*返回元素个数*/int size() const { return treeSize; }void inOrderThreaded() // 中序遍历索引,就是中序遍历的时候添加索引{pre = nullptr;inOrderThreaded(root);}/*中序遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/void inOrder(void(*theVisit)(inThreadedBinaryTreeNode<E>*)){visit = theVisit;/*是因为递归,所以才要这样的*/inOrder(root);/*这里调用的是静态成员函数inOrder()*/}/*中序遍历---输出endl*/void inOrderOutput() { inOrder(output); cout << endl; }/*后续遍历二叉树,使用函数指针的目的是是的本函数可以实现多种目的*/void postOrder(void(*theVisit)(inThreadedBinaryTreeNode<E>*)){visit = theVisit;/*是因为递归,所以才要这样的*/postOrder(root);/*这里调用的是静态成员函数inOrder()*/}/*后序遍历---输出endl*/void postOrderOutput() { postOrder(output); cout << endl; }/*清空二叉树 这里必须使用后序遍历 不然会出错*/void erase(){postOrder(dispose);root = nullptr;treeSize = 0;}/*输入时为了将root根节点传递给createBiTree()函数*/void input(void){createBiTree(root);}
private:
/*二叉树基础私有成员*/inThreadedBinaryTreeNode<E>* root;//指向根的指针int treeSize;//树的结点个数static inThreadedBinaryTreeNode<E>* pre;// 在线索化时使用的前驱tempstatic void (*visit)(inThreadedBinaryTreeNode<E>*);//是一个函数指针,返回值为void 函数参数为binaryTreeNode<E>*static void inOrder(inThreadedBinaryTreeNode<E>* t);static void inOrderThreaded(inThreadedBinaryTreeNode<E>* t);// 中序遍历索引,就是中序遍历的时候添加索引static void postOrder(inThreadedBinaryTreeNode<E>* t);static void dispose(inThreadedBinaryTreeNode<E>* t) { delete t; }static void output(inThreadedBinaryTreeNode<E>* t) { cout << t->element << " "; }/*创建二叉树---递归---作为私有成员只能被成员函数调用*/void createBiTree(inThreadedBinaryTreeNode<E>*& tree);
};
/*私有静态成员初始化*/
/*这里是静态函数指针成员的初始化,不初始化会引发LINK错误*/
template<class E>
void (*inThreadedBinaryTreeChains<E>::visit)(inThreadedBinaryTreeNode<E>*) = 0; // visit function
// 这个地方需要做一个初始化,不做的话就会bug
template<class E>
inThreadedBinaryTreeNode<E>* inThreadedBinaryTreeChains<E>:: pre = nullptr;
/*中序遍历 递归*/
/*不受索引影响的中序遍历*/
template<class E>
void inThreadedBinaryTreeChains<E>::inOrder(inThreadedBinaryTreeNode<E>* t)
{if (t != nullptr){// 在其左孩子不是索引时遍历if(!t->LTag)inOrder(t->leftChild);/*中序遍历左子树*/visit(t);/*访问树根*/// 在其右孩子不是索引时遍历if(!t->RTag)inOrder(t->rightChild);/*中序遍历右子树*/}
}
/*中序遍历索引 递归*/
/*本文写法可以保证在多次调用此函数下依然能正常执行,当插入新元素后再执行本函数可更新节点的索引*/
template<class E>
void inThreadedBinaryTreeChains<E>::inOrderThreaded(inThreadedBinaryTreeNode<E>* t)
{if (t != nullptr){if(!t->LTag)inOrderThreaded(t->leftChild);/*中序遍历左子树*/if(!t->leftChild || t->LTag) // 没有左孩子,或者是第二次遍历即左孩子指向了他的前驱{t->LTag = true;t->leftChild = pre;}if(pre){if(!pre->rightChild || t->RTag) // 如果前驱没有右孩子,或者是第二次遍历即右孩子指向了它的后继{pre->RTag = true;pre->rightChild = t;}}pre = t;if(!t->RTag)inOrderThreaded(t->rightChild);/*中序遍历右子树*/}
}
/*后序遍历 递归*/
/*不受索引影响的后序遍历*/
template<class E>
void inThreadedBinaryTreeChains<E>::postOrder(inThreadedBinaryTreeNode<E>* t)
{if (t != nullptr){// 在其左孩子不是索引时遍历if(!t->LTag)postOrder(t->leftChild);/*后序遍历左子树*/// 在其右孩子不是索引时遍历if(!t->LTag)postOrder(t->rightChild);/*后序遍历右子树*/visit(t);/*访问树根*/}
}/*创建二叉树---递归---模板的实现*/
template<class E>
void inThreadedBinaryTreeChains<E>::createBiTree(inThreadedBinaryTreeNode<E>*& tree)
{E data;cout << "Please enter the tree element:";while (!(cin >> data)){cin.clear();//清空标志位while (cin.get() != '\n')//删除无效的输入continue;cout << "Please enter the tree element:";}cin.get();/*针对char类型的特例*/if (typeid(data) == typeid(char)) {if (data == '#')tree = nullptr;else {treeSize++;tree = new inThreadedBinaryTreeNode<E>(data);createBiTree(tree->leftChild);createBiTree(tree->rightChild);}}else/*针对其他类型*/{if (data == 999)tree = nullptr;//当遇到999时,令树的根节点为nullptr,从而结束该分支的递归else{treeSize++;tree = new inThreadedBinaryTreeNode<E>(data);createBiTree(tree->leftChild);createBiTree(tree->rightChild);}}
}
#endif //_24THREADED_BINARYTREE_INTHREADEDBINARYTREE_H
inThreadedBinaryTreeChains.cpp
/*
Project name : _24Threaded_BinaryTree
Last modified Date: 2023年11月28日17点06分
Last Version: V1.0
Descriptions: 线索二叉树测试函数
*/
#include "inThreadedBinaryTreeChains.h"
void inThreadedBinaryTreeChainsTest(){cout << endl << "******************************inThreadedBinaryTreeChains()函数开始**********************************" << endl;cout << endl << "测试成员函数*******************************************" << endl;cout << "输入****************************" << endl;cout << "默认构造函数********************" << endl;inThreadedBinaryTreeChains<int> a;a.input();cout << "输出****************************" << endl;cout << "中序输出************************" << endl;//递归遍历a.inOrderThreaded();cout << "a.inOrderOutput() = ";a.inOrderOutput();cout << "后序输出************************" << endl;a.inOrderThreaded();cout << "a.postOrderOutput() = ";a.postOrderOutput();cout << "empty()*************************" << endl;cout << "a.empty() = " << a.empty() << endl;cout << "size()**************************" << endl;cout << "a.size() = " << a.size() << endl;cout << "erase()**************************" << endl;a.erase();cout << "a.inOrderOutput() = ";a.inOrderOutput();cout << "******************************inThreadedBinaryTreeChains()函数结束**********************************" << endl;
}
binaryTree.h
/*
Project name : allAlgorithmsTest
Last modified Date: 2022年8月27日09点43分
Last Version: V1.0
Descriptions: 二叉树的抽象类
*/#ifndef _24THREADED_BINARYTREE_BINARYTREE_H
#define _24THREADED_BINARYTREE_BINARYTREE_H
template<class T>
class binaryTree
{
public:virtual ~binaryTree() {}virtual bool empty() const = 0;virtual int size() const = 0;
// virtual void preOrder(void (*)(T*)) = 0;virtual void inOrder(void (*)(T*)) = 0;virtual void postOrder(void (*)(T*)) = 0;
// virtual void levelOrder(void (*)(T*)) = 0;
};
#endif //_24THREADED_BINARYTREE_BINARYTREE_H
inThreadedBinaryTreeNode.h
/*
Project name : _24Threaded_BinaryTree
Last modified Date: 2023年11月28日17点06分
Last Version: V1.0
Descriptions: 线索二叉树节点结构体
*/#ifndef _24THREADED_BINARYTREE_INTHREADEDBINARYTREENODE_H
#define _24THREADED_BINARYTREE_INTHREADEDBINARYTREENODE_H
template<class T>
struct inThreadedBinaryTreeNode
{T element;inThreadedBinaryTreeNode<T>* leftChild,//左子树*rightChild;//右子树bool LTag, RTag;// 左右子树指针是否为索引,为True则是索引,否则不是索引/*默认构造函数*/inThreadedBinaryTreeNode() { leftChild = rightChild = nullptr; LTag = RTag = false;}/*只初始化element*/inThreadedBinaryTreeNode(T melement){element = melement;leftChild = rightChild = nullptr;LTag = RTag = false;}/*三个元素都初始化*/inThreadedBinaryTreeNode(T melement, inThreadedBinaryTreeNode<T>* mleftChild, inThreadedBinaryTreeNode<T>* mrightChild){element = melement;leftChild = mleftChild;rightChild = mrightChild;LTag = RTag = false;}
};
#endif //_24THREADED_BINARYTREE_INTHREADEDBINARYTREENODE_H
测试
"C:\Users\15495\Documents\Jasmine\prj\_Algorithm\Data Structures, Algorithms and Applications in C++\_24Threaded BinaryTree\cmake-build-debug\_24Threaded_BinaryTree.exe"******************************inThreadedBinaryTreeChains()函数开始**********************************测试成员函数*******************************************
输入****************************
默认构造函数********************
Please enter the tree element:1
Please enter the tree element:2
Please enter the tree element:999
Please enter the tree element:999
Please enter the tree element:3
Please enter the tree element:999
Please enter the tree element:999
输出****************************
中序输出************************
a.inOrderOutput() = 2 1 3
后序输出************************
a.postOrderOutput() = 2 3 1
empty()*************************
a.empty() = 0
size()**************************
a.size() = 3
erase()**************************
a.inOrderOutput() =
******************************inThreadedBinaryTreeChains()函数结束**********************************Process finished with exit code 0
相关文章:

《数据结构、算法与应用C++语言描述》-线索二叉树的定义与C++实现
_23Threaded BinaryTree 可编译运行代码见:GIithub::Data-Structures-Algorithms-and-Applications/_24Threaded_BinaryTree 线索二叉树定义 在普通二叉树中,有很多nullptr指针被浪费了,可以将其利用起来。 首先我们要来看看这空指针有多少…...
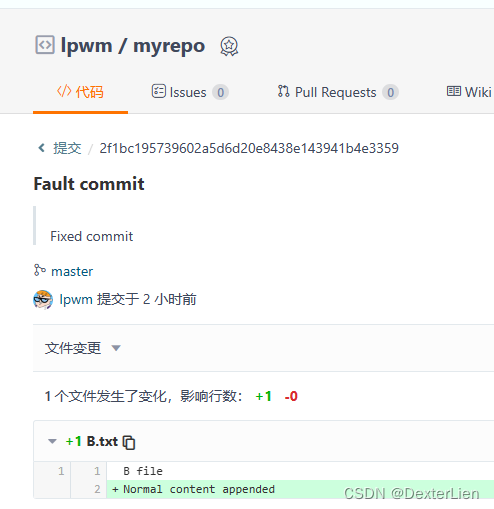
删除误提交的 git commit
背景描述 某次的意外 commit 中误将密码写到代码中并且 push 到了 remote repo 里面, 本文将围绕这个场景讨论如何弥补. 模拟误提交操作 在 Gitee 创建一个新的 Repo, clone 到本地 git clone https://gitee.com/lpwm/myrepo.git创建两个文件, commit 后 push 到 remote 作…...

机器学习---pySpark案例
1、统计PV,UV 1.if __name__ __main__: 2. conf SparkConf() 3. conf.setMaster("local") 4. conf.setAppName("test") 5. sc SparkContext(confconf) 6. 7. #pv 8. sc.textFile("./pvuv").map(lambda line:(l…...
【链表Linked List】力扣-24 两两交换链表中的节点
目录 题目描述 解题过程 题目描述 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 示例 1: 输入:he…...

企业微信协议开发,API接口调用
产品说明 一、 hook版本:企业微信hook接口是指将企业微信的功能封装成dll,并提供简易的接口给程序调用。通过hook技术,可以在不修改企业微信客户端源代码的情况下,实现对企业微信客户端的功能进行扩展和定制化。企业微信hook接口…...

代码随想录算法训练营 ---第五十五天
今天是 动态规划:编辑距离问题。 第一题: 简介: 动态规划五部曲: 1.确定dp数组的含义 dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。 2.确定递推公…...

【Intel/Altera】 全系列FPGA最新汇总说明,持续更新中
前言 2023年11月14日英特尔 FPGA中国技术日,Intel刚发布了新的FPGA系列,官网信息太多,我这里结合以前的信息,简单汇总更新一下,方便大家快速了解Intel/Altera FPGA家族。 目录 前言 Altera和Intel 型号汇总 1. Agi…...

利用flask将yolov5算法封装成在线推理服务
本脚本主要参考了yolov5工程文件夹下面的detect.py,将yolov5算法封装成了一个在线的推理服务,可以接受app请求,然后推理图片,并将检测结果以json返回,该服务可以供数据标注平台请求。 from flask import * import shutil import json import os import pynvml import pand…...

vue3父子传值实现弹框功能
在Vue3中,我们可以通过 provide 和 inject 来实现父子组件之间的数据传递,这也适用于实现弹框功能。下面是一个简单的例子: 父组件代码: <template><div><button click"showDialog">打开弹框</b…...

C++入门【2-C++ 数据类型】
C 数据类型 使用编程语言进行编程时,需要用到各种变量来存储各种信息。变量保留的是它所存储的值的内存位置。这意味着,当您创建一个变量时,就会在内存中保留一些空间。 您可能需要存储各种数据类型(比如字符型、宽字符型、整型…...

按照官网文档 通过useExtendedLib扩展库 引入WeUI,报错 组件未定义 | 解决办法
检查开发者工具版本是否过老 参考博客 不要使用 游客模式,游客模式不支持,请注册Appid 使用。 注意 扩展库方式 和 npm 方式不能同时使用,会有相应报错...

Chat-GPT原理
Chat-GPT原理核心:基于Transformer 架构 以下是参考文献的部分截图原文说明: Transformers are based on the “attention mechanism,” which allows the model to pay more attention to some inputs than others, regardless of where they show up in t…...
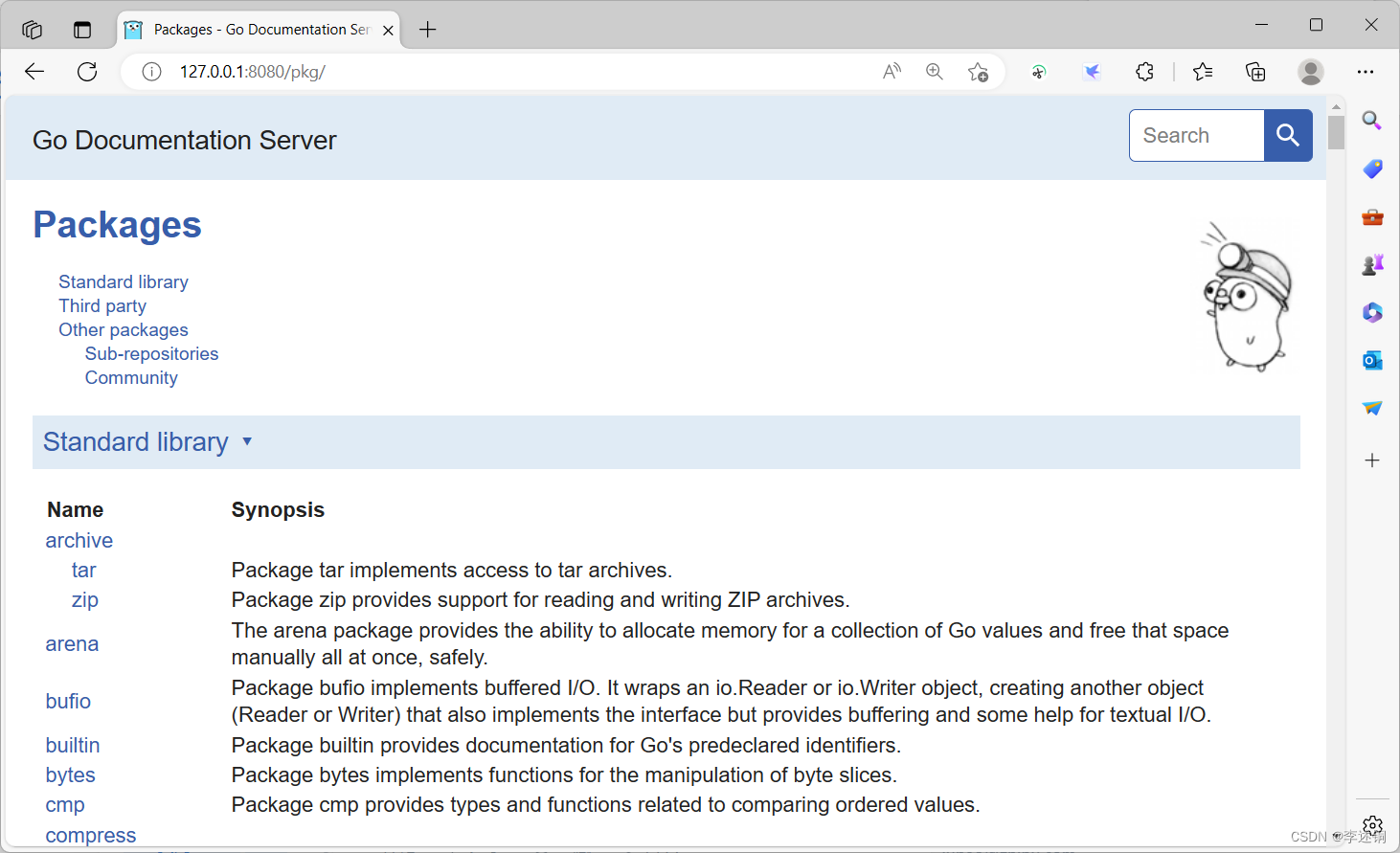
GODOC命令无效,原因是需要手动安装
在看《GO程序设计语言》这本书,按照其中的内容,想看下GO自带的包的文档。 书中讲,可以直接输入GoDOC命令来打开一个服务器,从而可以用浏览器访问文档库。输入命令后,系统提示找不到该命令。 查了资料后才发现ÿ…...

忽略python运行出现的大量警告
添加以下代码即可 import warnings warnings.filterwarnings(ignore)...
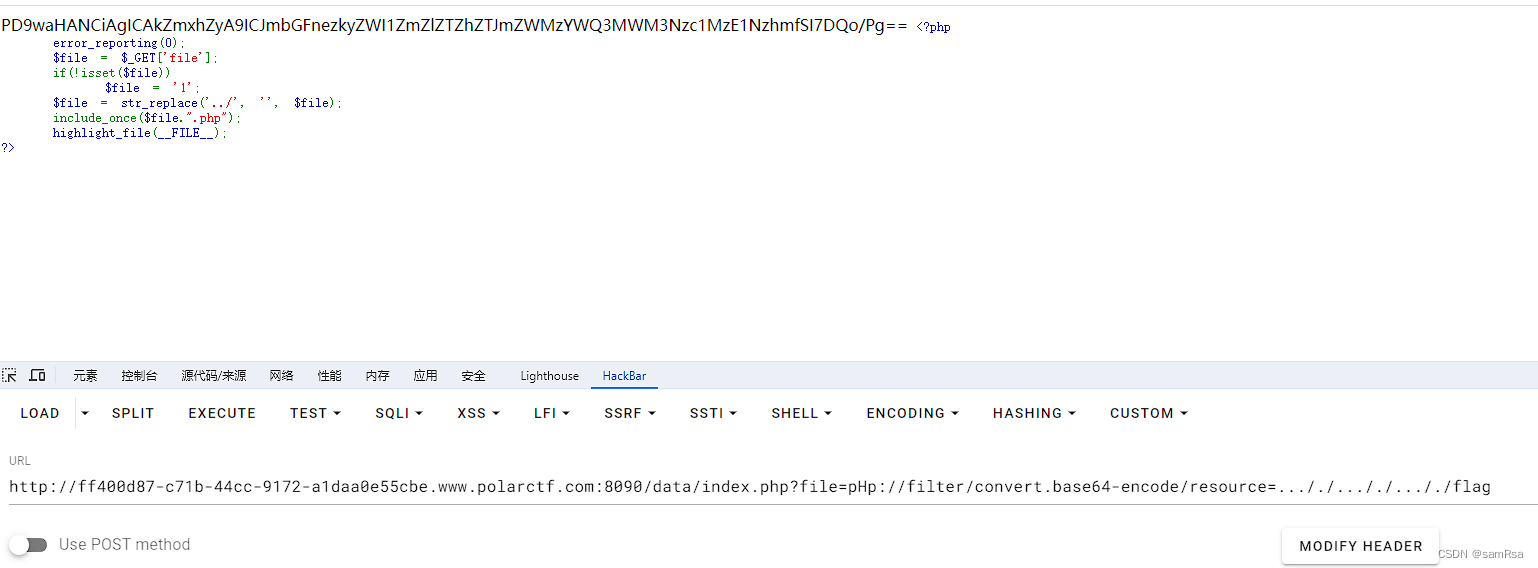
【Polar靶场WEB签到】
题目: <?phperror_reporting(0);$file $_GET[file];if(!isset($file))$file 1;$file str_replace(../, , $file);include_once($file.".php");highlight_file(__FILE__); ?>解答:1、进入index页面,说让你加弟弟&#x…...
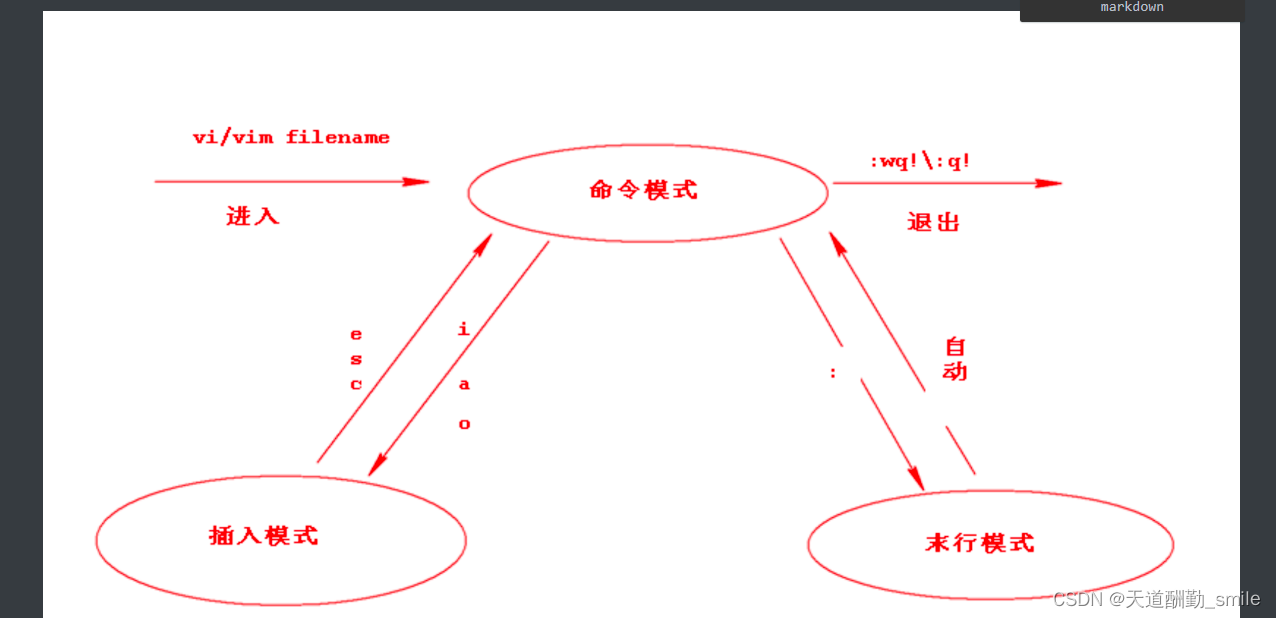
Linux详解——常用命令(二)
目录 一、常用命令 1.进程相关命令 2.vi命令 3.软件相关命令 RPM命令 YUM命令 4.用户和组相关命令 5.权限相关命令 一、常用命令 1.进程相关命令 # 1.ps 询在当前控制台上运行的进程 ps -aux 说明:查询系统中所有运行的进程,包括后台进程,其…...
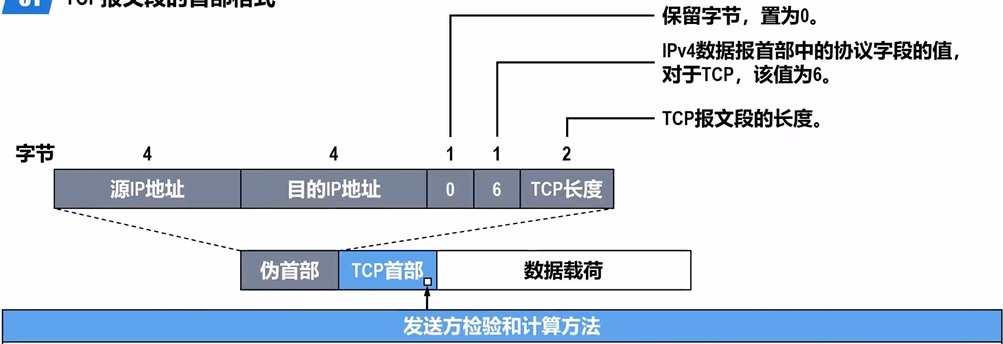
TCP首部格式_基本知识
TCP首部格式 表格索引: 源端口目的端口 序号 确认号 数据偏移保留 ACK等 窗口检验和紧急指针 TCP报文段首部格式图 源端口与目的端口: 各占16位 序号:占32比特,取值范围0~232-1。当序号增加到最后一个时,下一个序号又回到0。用来指出本TCP报文段数据载…...

MIT线性代数笔记-第23讲-微分方程,exp(At)
目录 23.微分方程, e x p ( A t ) exp(At) exp(At)用矩阵求解微分方程矩阵指数二阶常微分方程 打赏 23.微分方程, e x p ( A t ) exp(At) exp(At) 用矩阵求解微分方程 例: { d u 1 d t − u 1 2 u 2 d u 2 d t u 1 − 2 u 2 \left \{ \b…...
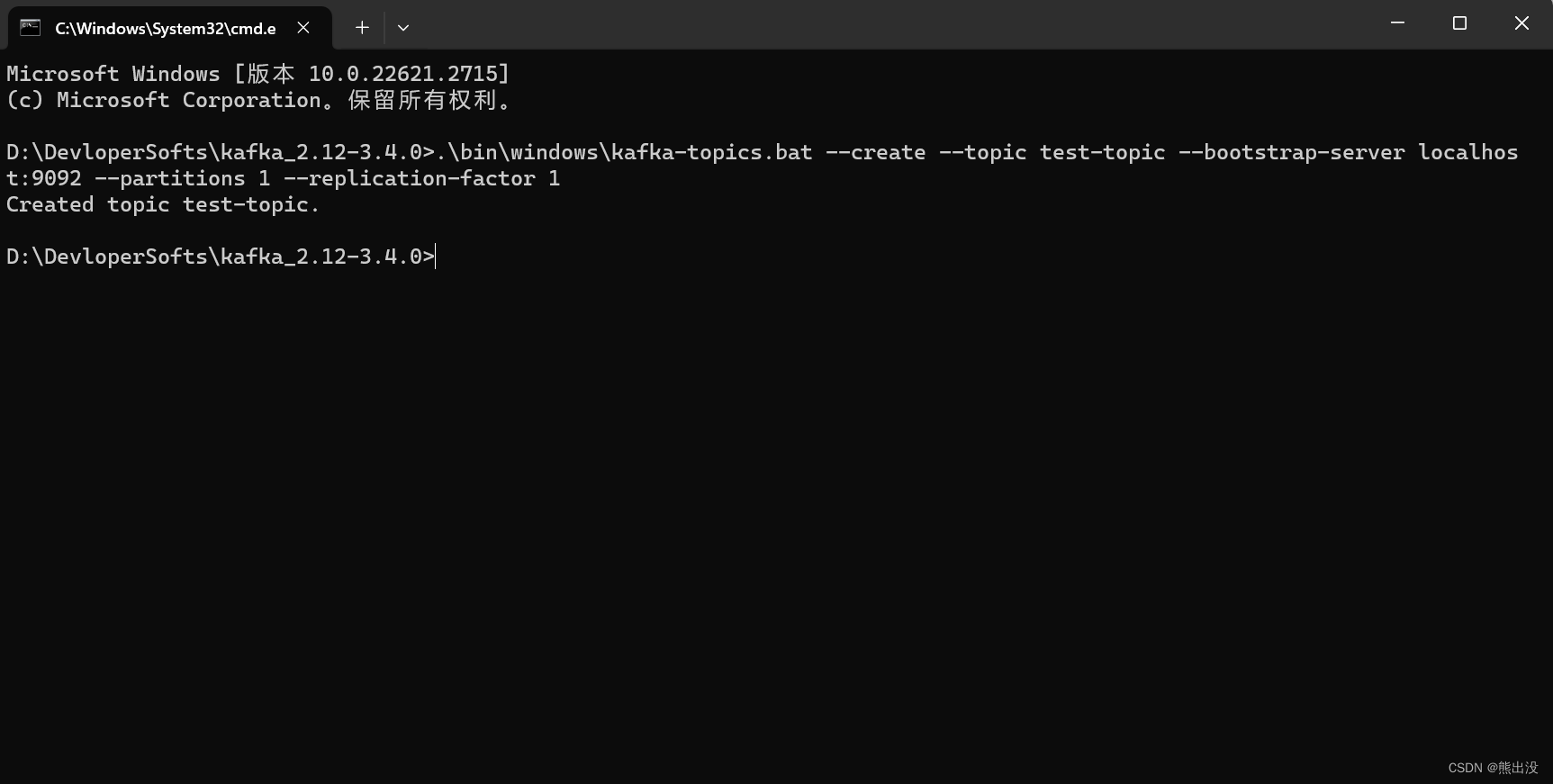
windows下安装配置kafka
一、安装zookeeper 在使用Kafka之前,通常需要先安装和配置ZooKeeper。ZooKeeper是Kafka的依赖项之一,它用于协调和管理Kafka集群的状态。 ZooKeeper是一个开源的分布式协调服务,它提供了可靠的数据存储和协调机制,用于协调分布式…...

TV遥控器模拟鼠标键
需求 : tv上部分app不支持光标选中,如亚马逊,插上鼠标不方便,即可以用遥控器模拟鼠标滚动和点击 1.拦截上下左右键 在WMS::PhoneWindowManager::interceptKeyBeforeQueueing中监听上下左右左右键,进行拦截。 Overrid…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
