【动态规划】LeetCode2111:使数组 K 递增的最少操作次数
作者推荐
[二分查找]LeetCode2040:两个有序数组的第 K 小乘积
本文涉及的基础知识点
二分查找算法合集
分组 动态规划
题目
给你一个下标从 0 开始包含 n 个正整数的数组 arr ,和一个正整数 k 。
如果对于每个满足 k <= i <= n-1 的下标 i ,都有 arr[i-k] <= arr[i] ,那么我们称 arr 是 K 递增 的。
比方说,arr = [4, 1, 5, 2, 6, 2] 对于 k = 2 是 K 递增的,因为:
arr[0] <= arr[2] (4 <= 5)
arr[1] <= arr[3] (1 <= 2)
arr[2] <= arr[4] (5 <= 6)
arr[3] <= arr[5] (2 <= 2)
但是,相同的数组 arr 对于 k = 1 不是 K 递增的(因为 arr[0] > arr[1]),对于 k = 3 也不是 K 递增的(因为 arr[0] > arr[3] )。
每一次 操作 中,你可以选择一个下标 i 并将 arr[i] 改成任意 正整数。
请你返回对于给定的 k ,使数组变成 K 递增的 最少操作次数 。
示例 1:
输入:arr = [5,4,3,2,1], k = 1
输出:4
解释:
对于 k = 1 ,数组最终必须变成非递减的。
可行的 K 递增结果数组为 [5,6,7,8,9],[1,1,1,1,1],[2,2,3,4,4] 。它们都需要 4 次操作。
次优解是将数组变成比方说 [6,7,8,9,10] ,因为需要 5 次操作。
显然我们无法使用少于 4 次操作将数组变成 K 递增的。
示例 2:
输入:arr = [4,1,5,2,6,2], k = 2
输出:0
解释:
这是题目描述中的例子。
对于每个满足 2 <= i <= 5 的下标 i ,有 arr[i-2] <= arr[i] 。
由于给定数组已经是 K 递增的,我们不需要进行任何操作。
示例 3:
输入:arr = [4,1,5,2,6,2], k = 3
输出:2
解释:
下标 3 和 5 是仅有的 3 <= i <= 5 且不满足 arr[i-3] <= arr[i] 的下标。
将数组变成 K 递增的方法之一是将 arr[3] 变为 4 ,且将 arr[5] 变成 5 。
数组变为 [4,1,5,4,6,5] 。
可能有其他方法将数组变为 K 递增的,但没有任何一种方法需要的操作次数小于 2 次。
提示:
1 <= arr.length <= 105
1 <= arr[i], k <= arr.length
分析
时间复杂度
O(nlogn),枚举每个元素,时间复杂度O(n),每个元素二分查找O(logn)。
代码
原理
一,有多少对不符合递增,则至少需要多少次操作。arr[i]和arr[i+1]不符合,需要修改arr[i]或arr[i+1]。能否一次修改,同时解决两个数对,假定arr[i-1] > arr[i] > arr[i+1],由于arr[i-1]>arr[i+1],所以arr[i]无论如何都不可能大于等于arr[i-1],同时小于等于arr[i+1]。
二,需要的操作数,可能大于非递增的对数。比如:4 1 3 ,4 1非递增,1 3递增。
三,操作次数等于=总元素数-最长递增序列的长度。假定最长子系列为:newNew[0]…newNew[n]。
四,第三只能说明是一个解,现在来证明是最优解: 假定arr2最优解,删掉修改过的元素,那么它一定是arr的子序列,且是递增的。此子系列越长,删除(操作)的元素越少。
| newNew[0]之前的元素 | 全部改成newNew[0] |
| newNew[n]之后的元素 | 全部改成newNew[n] |
| newNew[i]和newNew[i+1]的元素 | 全改成newNew[i] |
变量解释
| vLenMinEnd | vLenMinEnd[i]=x,在长度为i的子序列中,结尾的最小值为x |
核心代码
class Solution {
public:int kIncreasing(vector<int>& arr, int k) {int iMaxLen = 0;for (int i = 0; i < k; i++){vector<int> vLenMinEnd = { 0,arr[i] };for (int j = i + k; j < arr.size(); j += k){auto index = std::upper_bound(vLenMinEnd.begin(), vLenMinEnd.end(), arr[j])- vLenMinEnd.begin();if (index >= vLenMinEnd.size()){vLenMinEnd.emplace_back(arr[j]);continue;}vLenMinEnd[index] = min(vLenMinEnd[index], arr[j]); }iMaxLen += vLenMinEnd.size() - 1;}return arr.size()-iMaxLen;}
};
测试用例
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
assert(v1[i] == v2[i]);
}
}
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
int main()
{
vector arr;
int k, res;
{
Solution slu;
arr = { 12, 6, 12, 6, 14, 2, 13, 17, 3, 8, 11, 7, 4, 11, 18, 8, 8, 3 }, k = 1;
auto res = slu.kIncreasing(arr, k);
Assert(12, res);
}
{
Solution slu;
arr = { 5, 4, 3, 2, 1 }, k = 1;
auto res = slu.kIncreasing(arr,k);
Assert(4, res);
}
{
Solution slu;
arr = { 4,1,5,2,6,2 }, k = 2;
auto res = slu.kIncreasing(arr, k);
Assert(0, res);
}
{
Solution slu;
arr = { 4,1,5,2,6,2 }, k = 3;
auto res = slu.kIncreasing(arr, k);
Assert(2, res);
}
//CConsole::Out(res);
}
2023年9月旧代码
class Solution {
public:
int kIncreasing(vector& arr, int k) {
vector<vector> vSubArr(k);
for (int i = 0; i < arr.size(); i++)
{
vSubArr[i%k].push_back(arr[i]);
}
int iRet = 0;
for ( auto& v : vSubArr)
{
iRet += NeedChange(v, 0, v.size() );
}
return iRet;
}
int NeedChange(vector& arr,int iLeft,int iRight)
{
std::map<int, int> mValueNums;
for (const auto& a : arr)
{
auto it = mValueNums.upper_bound(a);
auto itTmp = it;
const int iValue = ((mValueNums.begin() == it) ? 0 : (–itTmp)->second) + 1;
if ((mValueNums.end() != it) && (it->second <= iValue))
{
mValueNums.erase(it);
}
mValueNums[a] = iValue;
}
return arr.size() - mValueNums.rbegin()->second;
}
int m_iK;
};
2023年9月第一版
class Solution {
public:
int kIncreasing(vector& arr, int k) {
int iRet = 0;
for (int turn = 0; turn < k; turn++)
{
std::map<int, int> mEndLen;
mEndLen[0] = 0;
int iMaxLen = 0;
for (int index = turn; index < arr.size(); index += k)
{
auto it = mEndLen.upper_bound(arr[index]);
const int iLen = std::prev(it)->second+1;
it = mEndLen.lower_bound(arr[index]);
auto ij = it;
for (; (ij != mEndLen.end()) && (ij->second <= iLen); ij++);
mEndLen.erase(it, ij);
mEndLen[arr[index]] = iLen;
iMaxLen = max(iMaxLen, iLen);
}
iRet += iMaxLen;
}
return arr.size()- iRet;
}
};
2023年9月第二版
class Solution {
public:
int kIncreasing(vector& arr, int k) {
int iRet = 0;
for (int turn = 0; turn < k; turn++)
{
vector vValue;
for (int index = turn; index < arr.size(); index += k)
{
auto it = std::upper_bound(vValue.begin(), vValue.end(),arr[index]);
if (vValue.end() == it)
{
vValue.emplace_back(arr[index]);
}
else
{
*it = arr[index];
}
}
iRet += vValue.size();
}
return arr.size()- iRet;
}
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业 |
。也就是我们常说的专业的人做专业的事。 |
|如果程序是一条龙,那算法就是他的是睛|
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境:
VS2022 C++17

相关文章:

【动态规划】LeetCode2111:使数组 K 递增的最少操作次数
作者推荐 [二分查找]LeetCode2040:两个有序数组的第 K 小乘积 本文涉及的基础知识点 二分查找算法合集 分组 动态规划 题目 给你一个下标从 0 开始包含 n 个正整数的数组 arr ,和一个正整数 k 。 如果对于每个满足 k < i < n-1 的下标 i ,都有…...

SpringCloud面试题——Nacos
一:什么是Nacos? 二:服务心跳与服务注册原理? 在spring容器启动的时候,nacos客户端会进行两步操作。 向nacos服务端发送心跳向nacos服务端注册当前服务 服务心跳 客户端在启动的时候,会开启一个心跳线程…...

leetcode:统计感冒序列的数目【数学题:组合数含逆元模版】
1. 题目截图 2.题目分析 需要把其分为多个段进行填充 长为k的段,从两端往中间填充的方案数有2 ** (k - 1)种 组合数就是选哪几个数填哪几个段即可 3.组合数含逆元模版 MOD 1_000_000_007 MX 100_000# 组合数模板 fac [0] * MX fac[0] 1 for i in range(1, MX…...

外贸建站平台工具推荐?做海洋建站的平台?
外贸建站平台用哪个比较好?独立站建站系统如何选择? 随着全球市场的竞争日益激烈,如何通过互联网渠道展示企业形象、吸引客户成为外贸企业亟待解决的问题。海洋建站将为大家介绍几款优秀的外贸建站平台工具,助力企业在数字化时代…...
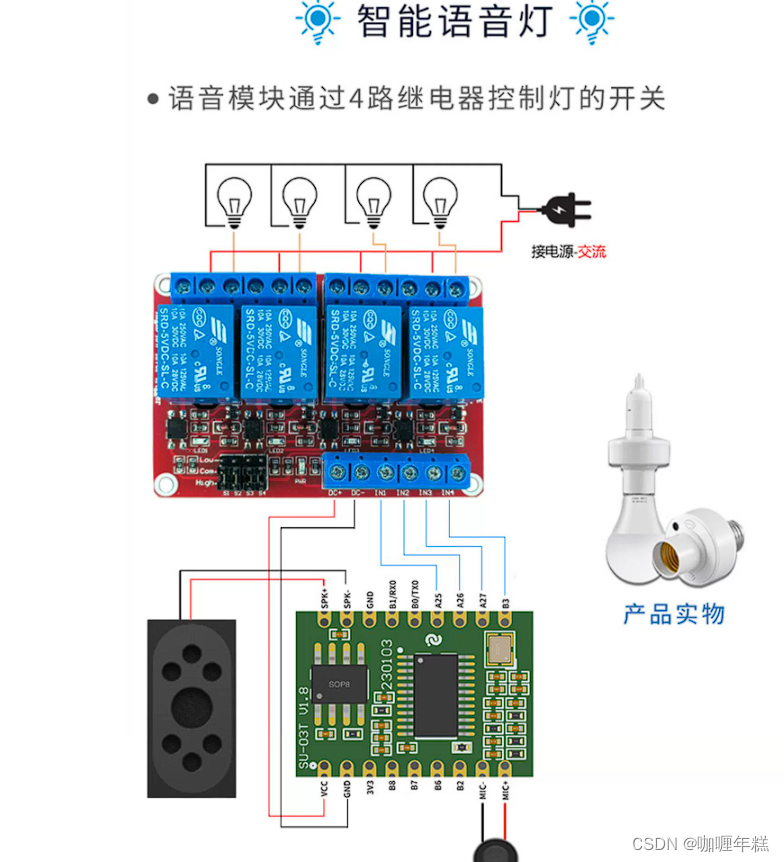
【智能家居】三、添加语音识别模块的串口读取功能点
语音识别模块SU-03T 串口通信线程控制代码 inputCommand.h(输入控制指令)voiceControl.c(语音控制模块指令)main.c(主函数)编译运行结果 语音识别模块SU-03T AI智能语音识别模块离线语音控制模块语音识别…...
物联网开发(一)新版Onenet 基础配置
onenet新创建的账号,没有了多协议接入,只有新的物联网开放平台 第一讲,先给大家讲一下:新版Onenet 基础配置 创建产品 产品开发-->创建产品 产品的品类选择个:大致符合你项目的即可,没有影响 选择智…...

qt/c/c++文件操作总结
1. 读取文件 1.1 Qt以二进制方式读取大文件返回char* 在Qt中以二进制模式读取一个大文件(以500MB为例)并将其内容存储到char*数组中,需要谨慎处理内存分配。以下是实现这一功能的步骤和示例代码: 1. 打开文件 使用QFile类以二进制模式打开文件。 2. 检查文件大小 使用…...

表示你的shell未被正确配置以使用conda activate--换成清华源anaconda
1 CommandNotFoundError: Your shell has not been properly configured to use conda activate. If using conda activate from a batch script, change your invocation to CALL conda.bat activate.To initialize your shell, run$ conda init <SHELL_NAME>这个错误提…...

VT-MRPA1-151-1X/V0/0控制2FRE16模块式模拟放大器
适用于控制带有电气位置反馈的直动式比例减压阀(DBETR- 1X 类型)或带有电气位置反馈的比例流量控制阀(2FRE... 类型);控制值输入 1 0 V(差动输入); 可分别调节“上/下”斜坡时间的斜…...
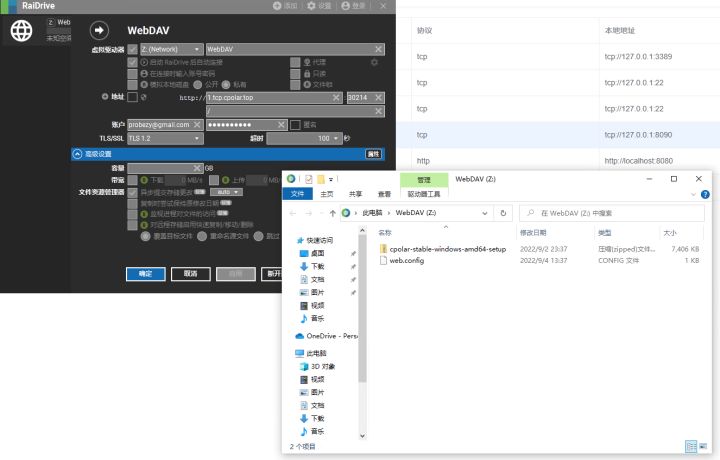
无需公网IP实现公网远程访问本地WebDAV服务
windows搭建WebDAV服务,并内网穿透公网访问【无公网IP】 文章目录 windows搭建WebDAV服务,并内网穿透公网访问【无公网IP】1. 安装IIS必要WebDav组件2. 客户端测试3. cpolar内网穿透3.1 打开Web-UI管理界面3.2 创建隧道3.3 查看在线隧道列表3.4 浏览器访…...
远程服务器QEMU+Ubuntu+GRUB+VNC最佳实践
远程服务器QEMUUbuntuGRUBVNC最佳实践 1. 准备2. QEMU启动安装Ubuntu2.1 服务器端2.2 本地端 3. 从服务器终端控制虚拟机GRUB与虚拟机终端 这段时间参与大量内核切换测试工作,实体机需要硬件自检太过笨重,因此主要通过QEMU验证正确性。有一个很大的问题是…...
macbook电脑运行缓慢和卡顿内存怎么清理了?
假如你还在为“你的系统内存不足”的提示所困扰,或者你的Mac电脑突然运行缓慢和卡顿,那么你一般需要认真了解一下macbook内存怎么清理了? MacBook是功能强大的电脑,这点毫无疑问,但是它仍旧会随着时间推移变得运行缓慢。值得庆幸…...

优化用户直播体验:第三方美颜SDK的前沿技术
当下,用户对于直播体验的要求日益提高,其中之一的重要方面就是实时美颜效果。第三方美颜SDK为直播平台和应用提供了强大的美颜功能,极大地改善了用户的直播观感。 一、背景与发展 过去,直播中的美颜往往依赖于主播或用户自行调整…...
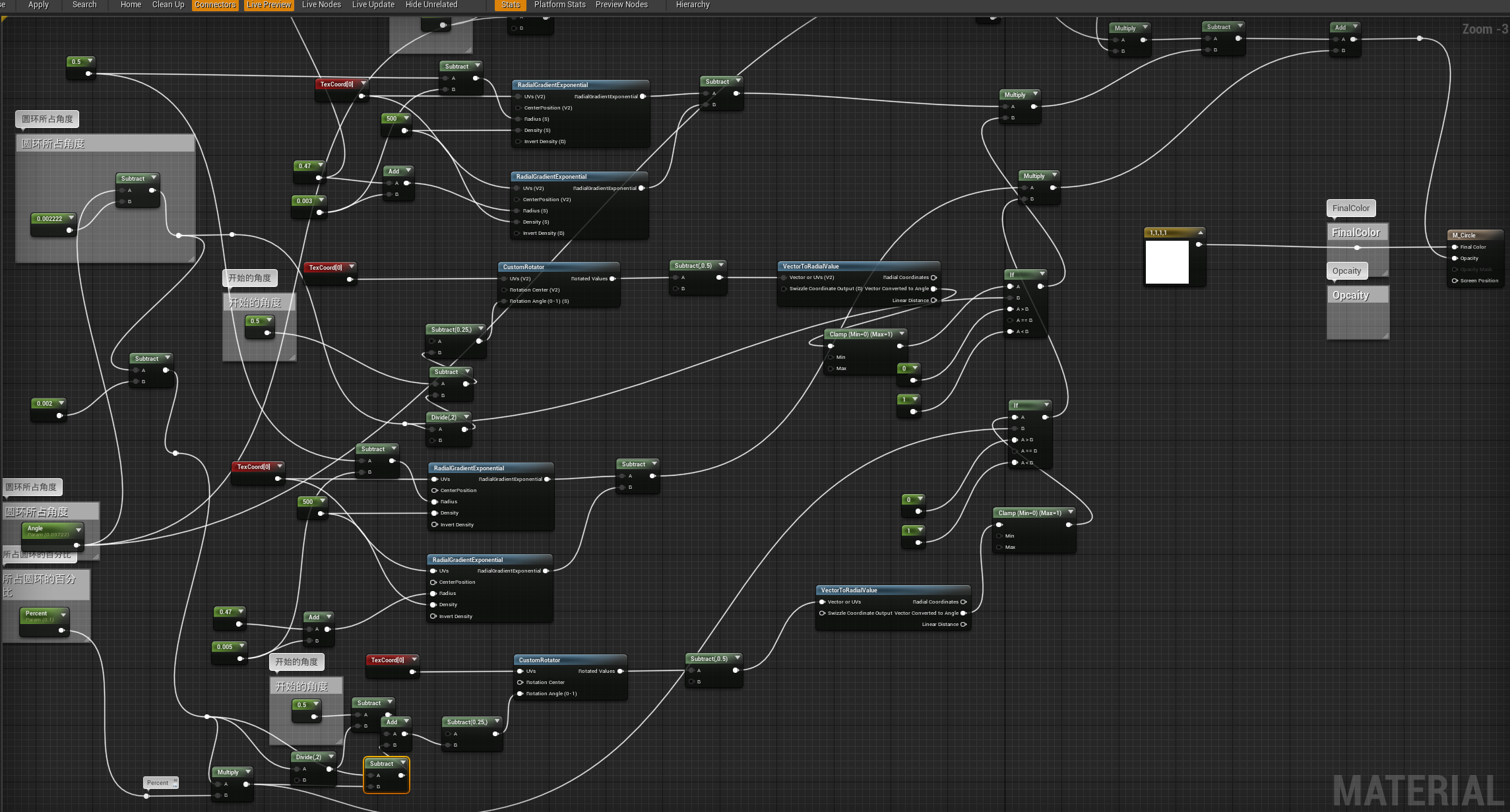
UE4/UE5 材质实现带框环形进度条
UE4/UE5 材质实现带框环形进度条 此处使用版本:UE4.27 原理:大圆减小圆可以得到圆环,大圆环减小圆环,可以得到圆环外围线框 实现效果: 实现(为了给大家放进一张面前能看的图,我费劲了心思&…...
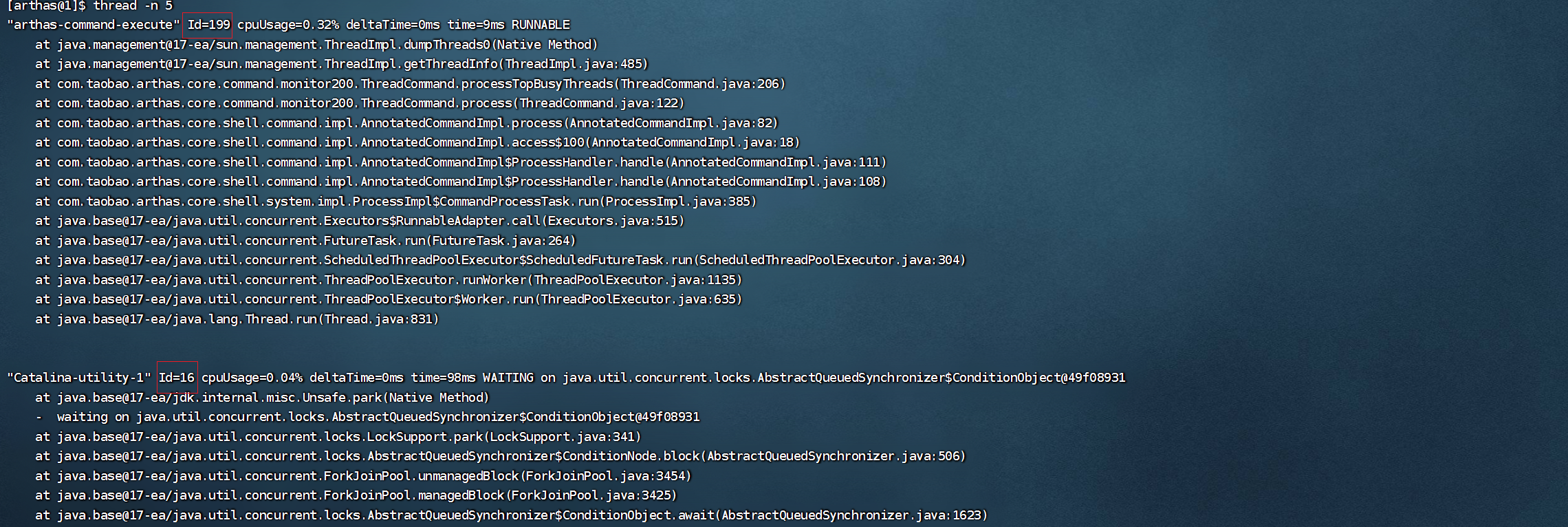
Docker 环境中 Spring Boot 应用的 Arthas 故障排查与性能优化实战
🚀 作者主页: 有来技术 🔥 开源项目: youlai-mall 🍃 vue3-element-admin 🍃 youlai-boot 🌺 仓库主页: Gitee 💫 Github 💫 GitCode 💖 欢迎点赞…...

Django 用户验证与权限管理
Django是一款强大且灵活的Python Web框架,不仅在构建功能复杂的网站应用中表现出色,还在诸如用户验证、权限管理等细微之处提供了优秀的解决方案。在多用户、权限复杂的Web应用中,认证和权限管理尤其重要。接下来,我们就来探究一下Django如何处理用户验证和权限管理的。 用…...
二手物品交易系统源码小程序H5闲置物品转让APP成品
这是一个二手物品交易系统的基本功能介绍,以下是对每个功能的详细解释: 商品发布:卖家可以通过系统发布二手商品信息,包括商品详情、价格、图片等。商品展示:系统会将所有发布的二手商品进行展示,买家可以…...
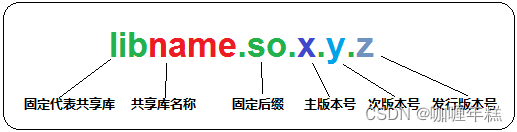
Linux库之动态库静态库
一、什么是库(Library) 二、库的分类 三、静态库、动态库优缺点 四、静态库的制作和使用 五、动态库的制作和使用 SO-NAME–解决主版本号之间的兼容问题 基于符号的版本机制 共享库系统路径 共享库的查找过程 有用的环境变量 gcc 编译器常用选项 Linux共…...

xilinx系列FPGA基于VIVADO的pin delay列表生成说明
目录 1 概述2 示例平台3 操作说明4 注意事项 xilinx系列FPGA基于VIVADO的pin delay列表生成说明 1 概述 本文用于讲诉xilinx系列FPGA基于VIVADO的pin delay列表生成说明,以及一些注意事项,为FPGA设计人员探明道路。 Pin delay 即FPGA内部die到pin的延时…...

1.vue学习笔记(vue简介+API风格+开发前的准备)
1.介绍 1.一款用于构建用户页面的JavaScript框架 2.基于HTML、CSS、JavaScript 3.官方文档:cn.vuejs.org2.渐进式框架 1.注重灵活性/可被逐步集成 根据需求场景:1.无需构建步骤,渐进式增强静态的HTML2.在任何页面中作为Web Components嵌入&…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

【Java多线程从青铜到王者】单例设计模式(八)
wait和sleep的区别 我们的wait也是提供了一个还有超时时间的版本,sleep也是可以指定时间的,也就是说时间一到就会解除阻塞,继续执行 wait和sleep都能被提前唤醒(虽然时间还没有到也可以提前唤醒),wait能被notify提前唤醒…...
