ZKP Understanding Nova (1): MinRoot Example
Understanding Nova
Kothapalli, Abhiram, Srinath Setty, and Ioanna Tzialla. “Nova: Recursive zero-knowledge arguments from folding schemes.” Annual International Cryptology Conference. Cham: Springer Nature Switzerland, 2022.
Nova: Paper Code
1. Understanding the MinRoot Example
type E1 = Bn256EngineKZG;
type E2 = GrumpkinEngine;
type EE1 = nova_snark::provider::mlkzg::EvaluationEngine<E1>;
type EE2 = nova_snark::provider::ipa_pc::EvaluationEngine<E2>;
type S1 = nova_snark::spartan::snark::RelaxedR1CSSNARK<E1, EE1>; // non-preprocessing SNARK
type S2 = nova_snark::spartan::snark::RelaxedR1CSSNARK<E2, EE2>; // non-preprocessing SNARK
- 定义了一些type
struct MinRootIteration<G: Group> {x_i: G::Scalar,y_i: G::Scalar,x_i_plus_1: G::Scalar,y_i_plus_1: G::Scalar,
}
这段代码定义了一个名为 MinRootIteration 的结构体,它是用于表示最小根迭代的数据结构。这个结构体需要一个泛型参数 G,这个参数必须实现了 Group trait。
在这个结构体中,我们定义了四个字段,它们都是 G::Scalar 类型。这个类型是由 Group trait 定义的关联类型,通常用于表示一个群的标量值。
具体来说,这四个字段分别是:
- x_i:表示当前迭代的 x 值。
- y_i:表示当前迭代的 y 值。
- x_i_plus_1:表示下一次迭代的 x 值。
- y_i_plus_1:表示下一次迭代的 y 值。
这个结构体可能被用于存储和管理在最小根迭代过程中的数据。
impl<G: Group> MinRootIteration<G> {// produces a sample non-deterministic advice, executing one invocation of MinRoot per stepfn new(num_iters: usize, x_0: &G::Scalar, y_0: &G::Scalar) -> (Vec<G::Scalar>, Vec<Self>) {// exp = (p - 3 / 5), where p is the order of the group// x^{exp} mod p provides the fifth root of xlet exp = {let p = G::group_params().2.to_biguint().unwrap();let two = BigUint::parse_bytes(b"2", 10).unwrap();let three = BigUint::parse_bytes(b"3", 10).unwrap();let five = BigUint::parse_bytes(b"5", 10).unwrap();let five_inv = five.modpow(&(&p - &two), &p);(&five_inv * (&p - &three)) % &p};
为什么这段代码得到 exp = (p - 3) / 5 mod p?
- let p = G::group_params().2.to_biguint().unwrap();
- 从一个类型为 G 的结构体中获取群组参数,并提取第三个元素作为整数 p。
- to_biguint().unwrap() 将其转换为大整数类型 (BigUint)。
- let two = BigUint::parse_bytes(b"2", 10).unwrap();
- 创建一个大整数 two,其值为 2。
- let three = BigUint::parse_bytes(b"3", 10).unwrap();
- 创建一个大整数 three,其值为 3。
- let five = BigUint::parse_bytes(b"5", 10).unwrap();
- 创建一个大整数 five,其值为 5。
- let five_inv = five.modpow(&(&p - &two), &p);
- 计算 5 的逆元(模 p 的情况下)。
- 逆元的计算使用了模幂运算,即 5 的 (p - 2) 次方模 p。
- (&five_inv * (&p - &three)) % &p
- 计算 (&p - &three) 乘以 five_inv 的结果,并对 p 取模。
- 最终的计算结果被赋值给变量 exp,它表示 (p - 3) / 5 的值,将用于后续的模运算,以获得给定数的五次方根。
关于第5步:
涉及到模运算中的欧拉定理(Euler’s theorem)和费马小定理(Fermat’s little theorem)。
费马小定理表明,如果 p 是一个质数,且 a 是不可被 p 整除的整数,那么 a^{p-1} mod p 等于 1。这是费马小定理的简化版本,而对于逆元的情况,我们可以将 a^{p-1} mod p 表示为 a^{p-2} mod p。
在这里,5^{p-2} mod p 表示的是 5 在模 p 的情况下的逆元。这是因为 p 是一个大于 5 的质数,所以根据费马小定理,5^{p-1} mod p 等于 1,从而 5^{p-2} mod p 就是 5 在模 p 的情况下的逆元。
逆元的概念是一个数在给定模下的乘法逆元,即与该数相乘的结果模该数的模等于 1。在这个场景中,计算 5^{p-2} mod p 就是为了得到 5 在模 p 的情况下的逆元,以便进行后续的乘法操作。
let mut res = Vec::new();let mut x_i = *x_0;let mut y_i = *y_0;for _i in 0..num_iters {let x_i_plus_1 = (x_i + y_i).pow_vartime(&exp.to_u64_digits()); // computes the fifth root of x_i + y_i// sanity checkif cfg!(debug_assertions) {let sq = x_i_plus_1 * x_i_plus_1;let quad = sq * sq;let fifth = quad * x_i_plus_1;assert_eq!(fifth, x_i + y_i);}let y_i_plus_1 = x_i;res.push(Self {x_i,y_i,x_i_plus_1,y_i_plus_1,});x_i = x_i_plus_1;y_i = y_i_plus_1;}let z0 = vec![*x_0, *y_0];(z0, res)}
let mut res = Vec::new();
- 创建一个可变的空向量 res,用于存储计算的结果。
let mut x_i = *x_0;
- 初始化一个可变变量 x_i,其初始值为 x_0 的值。
let mut y_i = *y_0;
- 初始化一个可变变量 y_i,其初始值为 y_0 的值。
for _i in 0..num_iters {
- 开始一个循环,迭代 num_iters 次。
let x_i_plus_1 = (x_i + y_i).pow_vartime(&exp.to_u64_digits());
- 计算 x_i + y_i 的五次方根,其中 exp 是之前计算得到的指数。
if cfg!(debug_assertions) { ... }
- 在调试模式下进行断言检查。这里执行了一个“sanity check”(合理性检查),确保计算的结果满足一定的条件。具体地,它验证了 x_i_plus_1 是否满足 (x_i_plus_1)^5 == x_i + y_i。
let y_i_plus_1 = x_i;
- 计算下一个 y_i 的值,赋值给 y_i_plus_1。
res.push(Self { ... });
- 将当前循环迭代的结果以结构体的形式存储在向量 res 中。
x_i = x_i_plus_1;
- 更新 x_i 的值为下一次迭代计算得到的 x_i_plus_1。
y_i = y_i_plus_1;
- 更新 y_i 的值为下一次迭代计算得到的 y_i_plus_1。
let z0 = vec![*x_0, *y_0];(z0, res);
- 循环结束后,创建一个包含初始输入值 x_0 和 y_0 的向量 z0。返回包含 z0 和 res 的元组。
整体而言,这段代码执行了一系列的计算和更新操作,产生了一组结果,这些结果以结构体的形式存储在向量 res 中。在每次迭代中,通过计算 (x_i + y_i)^{1/5},将 x_i 和 y_i 更新为下一轮迭代的值。在调试模式下,还进行了一个断言检查,确保计算的结果符合预期的数学性质。
#[derive(Clone, Debug)]
struct MinRootCircuit<G: Group> {seq: Vec<MinRootIteration<G>>,
}impl<G: Group> StepCircuit<G::Scalar> for MinRootCircuit<G> {fn arity(&self) -> usize {2}fn synthesize<CS: ConstraintSystem<G::Scalar>>(&self,cs: &mut CS,z: &[AllocatedNum<G::Scalar>],) -> Result<Vec<AllocatedNum<G::Scalar>>, SynthesisError> {let mut z_out: Result<Vec<AllocatedNum<G::Scalar>>, SynthesisError> =Err(SynthesisError::AssignmentMissing);// use the provided inputslet x_0 = z[0].clone();let y_0 = z[1].clone();// variables to hold running x_i and y_ilet mut x_i = x_0;let mut y_i = y_0;for i in 0..self.seq.len() {// non deterministic advicelet x_i_plus_1 =AllocatedNum::alloc(cs.namespace(|| format!("x_i_plus_1_iter_{i}")), || {Ok(self.seq[i].x_i_plus_1)})?;// check the following conditions hold:// (i) x_i_plus_1 = (x_i + y_i)^{1/5}, which can be more easily checked with x_i_plus_1^5 = x_i + y_i// (ii) y_i_plus_1 = x_i// (1) constraints for condition (i) are below// (2) constraints for condition (ii) is avoided because we just used x_i wherever y_i_plus_1 is usedlet x_i_plus_1_sq = x_i_plus_1.square(cs.namespace(|| format!("x_i_plus_1_sq_iter_{i}")))?;let x_i_plus_1_quad =x_i_plus_1_sq.square(cs.namespace(|| format!("x_i_plus_1_quad_{i}")))?;cs.enforce(|| format!("x_i_plus_1_quad * x_i_plus_1 = x_i + y_i_iter_{i}"),|lc| lc + x_i_plus_1_quad.get_variable(),|lc| lc + x_i_plus_1.get_variable(),|lc| lc + x_i.get_variable() + y_i.get_variable(),);if i == self.seq.len() - 1 {z_out = Ok(vec![x_i_plus_1.clone(), x_i.clone()]);}// update x_i and y_i for the next iterationy_i = x_i;x_i = x_i_plus_1;}z_out}
}- MinRootCircuit 结构体:
- 定义了一个包含 MinRootIteration 结构体的向量 seq 的结构体。
- 实现了 Clone 和 Debug trait,使得该结构体可以被克隆和打印调试信息。
- StepCircuit trait 实现:
- 该 trait 提供了电路执行的接口,用于计算电路的输出。
- arity 方法返回电路的输入数量,这里是2。
- synthesize 方法用于在给定的约束系统 CS 上执行电路的计算。
- synthesize 方法具体实现:
- 创建一个用于保存输出的 Result 对象 z_out,初始值为 Err(SynthesisError::AssignmentMissing)。
- 通过模式匹配和 let 语句从输入数组 z 中获取两个输入 x_0 和 y_0。
- 使用 for 循环遍历迭代序列 self.seq 中的元素。
- 在循环中:
- 使用 AllocatedNum::alloc 创建一个新的分配数字 x_i_plus_1,其值来自于 self.seq[i].x_i_plus_1。
- 根据给定的条件,执行一些约束操作,确保 (x_i + y_i)^{1/5} = x_i_plus_1。
- 如果当前迭代是最后一次迭代,将 z_out 更新为包含 x_i_plus_1 和 x_i 的 Ok 值。
- 更新 x_i 和 y_i 为下一次迭代做准备。
- 返回最终的 z_out。
fn main() {println!("Nova-based VDF with MinRoot delay function");println!("=========================================================");let num_steps = 10;for num_iters_per_step in [1024, 2048, 4096, 8192, 16384, 32768, 65536] {// number of iterations of MinRoot per Nova's recursive step...
}
- 测试代码的主循环,分别设置每Nova递归步长MinRoot的迭代次数num_iters_per_step为[1024, 2048, 4096, 8192, 16384, 32768, 65536]
let circuit_primary = MinRootCircuit {seq: vec![MinRootIteration {x_i: <E1 as Engine>::Scalar::zero(),y_i: <E1 as Engine>::Scalar::zero(),x_i_plus_1: <E1 as Engine>::Scalar::zero(),y_i_plus_1: <E1 as Engine>::Scalar::zero(),};num_iters_per_step],};let circuit_secondary = TrivialCircuit::default();println!("Proving {num_iters_per_step} iterations of MinRoot per step");- 参考资料:https://www.youtube.com/watch?v=gopJn_QAdqU
- circuit_primary 是业务电路,具体为MinRootCircuit。
- circuit_secondary是trivial电路,被初始化为TrivialCircuit的default值。
- 初始化x_i ,y_i ,x_i_plus_1 ,y_i_plus_1 都初始化为0
// produce public parameters
let start = Instant::now();
println!("Producing public parameters...");
let pp = PublicParams::<E1,E2,MinRootCircuit<<E1 as Engine>::GE>,TrivialCircuit<<E2 as Engine>::Scalar>,
>::setup(&circuit_primary,&circuit_secondary,&*S1::ck_floor(),&*S2::ck_floor(),
);
println!("PublicParams::setup, took {:?} ", start.elapsed());- 在创建 PublicParams 实例的过程中,我们调用了 PublicParams::setup 方法。这个方法接受四个参数:circuit_primary、circuit_secondary、S1::ck_floor() 和 S2::ck_floor()。这四个参数分别表示主从电路,以及两个不同引擎的公共参数。
- ck: CommitmentKey
- Some final compressing SNARKs, like variants of Spartan, use computation commitments that require larger sizes for these parameters. These SNARKs provide a hint for these values by implementing RelaxedR1CSSNARKTrait::ck_floor(), which can be passed to this function.
// produce non-deterministic advice
let (z0_primary, minroot_iterations) = MinRootIteration::<<E1 as Engine>::GE>::new(num_iters_per_step * num_steps,&<E1 as Engine>::Scalar::zero(),&<E1 as Engine>::Scalar::one(),
);
let minroot_circuits = (0..num_steps).map(|i| MinRootCircuit {seq: (0..num_iters_per_step).map(|j| MinRootIteration {x_i: minroot_iterations[i * num_iters_per_step + j].x_i,y_i: minroot_iterations[i * num_iters_per_step + j].y_i,x_i_plus_1: minroot_iterations[i * num_iters_per_step + j].x_i_plus_1,y_i_plus_1: minroot_iterations[i * num_iters_per_step + j].y_i_plus_1,}).collect::<Vec<_>>(),}).collect::<Vec<_>>();let z0_secondary = vec![<E2 as Engine>::Scalar::zero()];- 首先,我们调用了 MinRootIteration::new 方法来创建一个新的 MinRootIteration 实例,这个实例包含了 z0_primary 和 minroot_iterations 两个部分。MinRootIteration::new 方法接受三个参数:num_iters_per_step * num_steps,::Scalar::zero() 和 ::Scalar::one()。表示我们要进行 num_iters_per_step * num_steps 次的最小根迭代,初始的 x 值为 0,初始的 y 值为 1。
- 然后,我们创建了一个名为 minroot_circuits 的向量,这个向量包含了 num_steps 个 MinRootCircuit 实例。每个 MinRootCircuit 实例都包含了一个 seq 字段,这个字段是一个向量,包含了 num_iters_per_step 个 MinRootIteration 实例。每个 MinRootIteration 实例都是从 minroot_iterations 向量中取出的,取出的方式是通过计算 i * num_iters_per_step + j 来获取索引。
- 最后,我们创建了一个名为 z0_secondary 的向量,这个向量只包含了一个元素,这个元素是 ::Scalar::zero()。这可能表示在第二个引擎中,我们的初始 z 值为 0。
type C1 = MinRootCircuit<<E1 as Engine>::GE>;
type C2 = TrivialCircuit<<E2 as Engine>::Scalar>;
// produce a recursive SNARK
println!("Generating a RecursiveSNARK...");
let mut recursive_snark: RecursiveSNARK<E1, E2, C1, C2> =RecursiveSNARK::<E1, E2, C1, C2>::new(&pp,&minroot_circuits[0],&circuit_secondary,&z0_primary,&z0_secondary,).unwrap();for (i, circuit_primary) in minroot_circuits.iter().enumerate() {let start = Instant::now();let res = recursive_snark.prove_step(&pp, circuit_primary, &circuit_secondary);assert!(res.is_ok());println!("RecursiveSNARK::prove_step {}: {:?}, took {:?} ",i,res.is_ok(),start.elapsed());
}
- 首先定义了两种类型别名 C1 和 C2,分别对应 MinRootCircuit 和 TrivialCircuit 结构体。这两个结构体都需要一个泛型参数,分别是 E1 和 E2 引擎的关联类型。
- 然后,我们创建了一个名为 recursive_snark 的 RecursiveSNARK 实例。RecursiveSNARK 是一个泛型结构体,需要四个类型参数:E1、E2、C1 和 C2。在创建 RecursiveSNARK 实例的过程中,我们调用了 RecursiveSNARK::new 方法。这个方法接受五个参数:pp、minroot_circuits[0]、circuit_secondary、z0_primary 和 z0_secondary。这五个参数分别表示公共参数、主电路、次电路,以及两个初始的 z 值。
- 接下来,我们遍历 minroot_circuits 向量中的每一个元素。对于每一个元素,我们都调用了 recursive_snark.prove_step 方法。这个方法接受三个参数:pp、circuit_primary 和 circuit_secondary,并返回一个 Result 类型的值,表示证明步骤的结果。如果证明步骤成功,Result 的值将是 Ok;如果失败,Result 的值将是 Err。
- 最后,我们使用 assert! 宏来检查 Result 的值。如果 Result 的值是 Err,assert! 宏将会触发一个 panic,程序将会终止运行。我们还使用 println! 宏来打印出每一步证明的结果和所花费的时间。
// verify the recursive SNARK
println!("Verifying a RecursiveSNARK...");
let start = Instant::now();
let res = recursive_snark.verify(&pp, num_steps, &z0_primary, &z0_secondary);
println!("RecursiveSNARK::verify: {:?}, took {:?}",res.is_ok(),start.elapsed()
);
assert!(res.is_ok());
- 验证 RecursiveSNARK
// produce a compressed SNARKprintln!("Generating a CompressedSNARK using Spartan with multilinear KZG...");let (pk, vk) = CompressedSNARK::<_, _, _, _, S1, S2>::setup(&pp).unwrap();let start = Instant::now();let res = CompressedSNARK::<_, _, _, _, S1, S2>::prove(&pp, &pk, &recursive_snark);println!("CompressedSNARK::prove: {:?}, took {:?}",res.is_ok(),start.elapsed());assert!(res.is_ok());let compressed_snark = res.unwrap();let mut encoder = ZlibEncoder::new(Vec::new(), Compression::default());bincode::serialize_into(&mut encoder, &compressed_snark).unwrap();let compressed_snark_encoded = encoder.finish().unwrap();println!("CompressedSNARK::len {:?} bytes",compressed_snark_encoded.len());// verify the compressed SNARKprintln!("Verifying a CompressedSNARK...");let start = Instant::now();let res = compressed_snark.verify(&vk, num_steps, &z0_primary, &z0_secondary);println!("CompressedSNARK::verify: {:?}, took {:?}",res.is_ok(),start.elapsed());assert!(res.is_ok());
- 证明/验证CompressedSNARK。
遗留问题:
[ ] PrimaryCircuit 和 SecondaryCircuit
[ ] RecursiveSNARK 和 CompressedSNARK
相关文章:
: MinRoot Example)
ZKP Understanding Nova (1): MinRoot Example
Understanding Nova Kothapalli, Abhiram, Srinath Setty, and Ioanna Tzialla. “Nova: Recursive zero-knowledge arguments from folding schemes.” Annual International Cryptology Conference. Cham: Springer Nature Switzerland, 2022. Nova: Paper Code 1. Unders…...
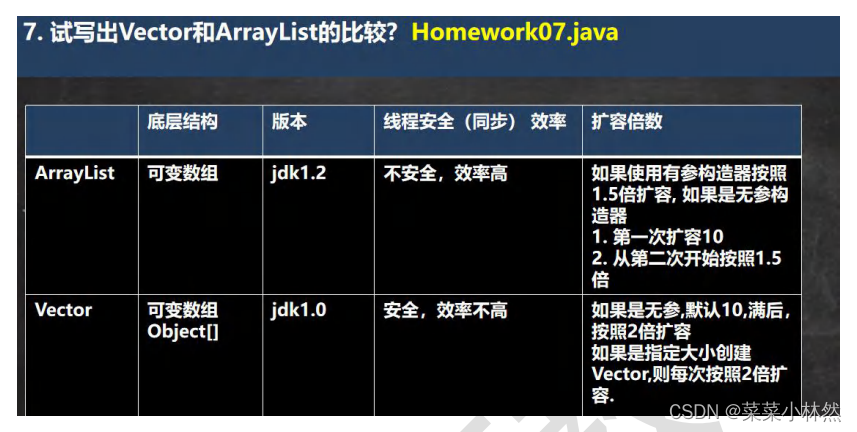
0基础学java-day14
一、集合 前面我们保存多个数据使用的是数组,那么数组有不足的地方,我们分析一下 1.数组 2 集合 数据类型也可以不一样 3.集合的框架体系 Java 的集合类很多,主要分为两大类,如图 :[背下来] package com.hspedu.c…...

创建conan包-工具链
创建conan包-工具链 1 Toolchains 本文是基于对conan官方文档Toolchains翻译而来, 更详细的信息可以去查阅conan官方文档。 1 Toolchains Toolchains are the new way to integrate with build systems in Conan. Recipes can define a generate() method that wi…...
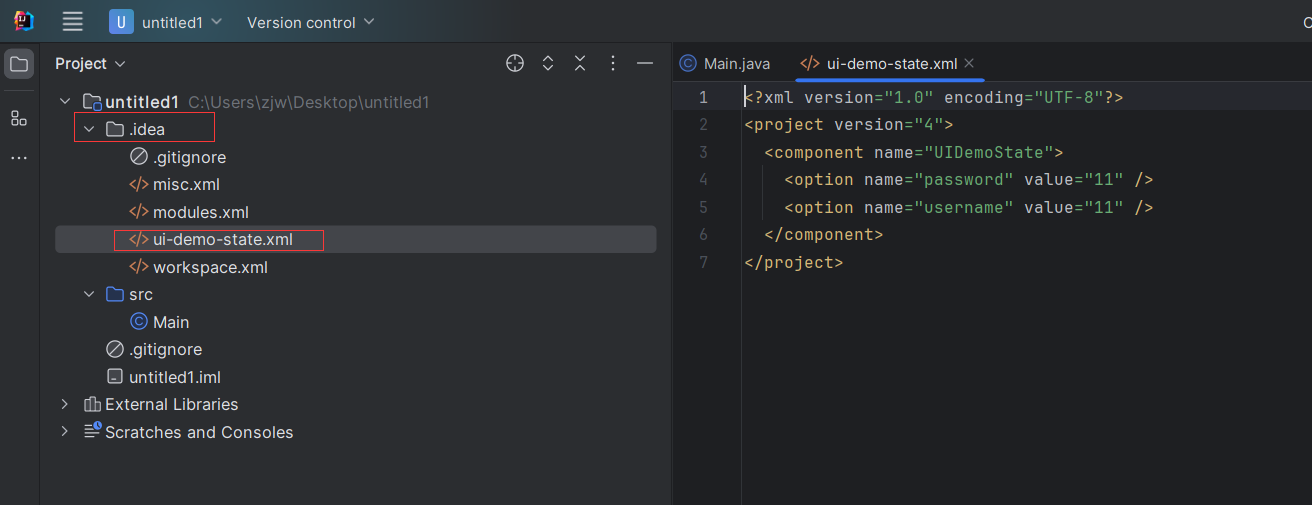
IntelliJ IDE 插件开发 | (二)UI 界面与数据持久化
系列文章 IntelliJ IDE 插件开发 |(一)快速入门 前言 在上一篇文章中介绍了在IDEA下开发、运行和安装插件的基本步骤,因此创建项目等基础步骤不再赘述,本文则开始介绍如何进行 UI 界面的开发以及相关数据的持久化存储ÿ…...

使用vue UI安装路由插件
1.使用vue创建项目 vue create vue-appvue ui 2.使用vue ui界面创建管理项目 终端页面输入:vue ui 创建项目 安装完成。可以直接在ui界面运行,也可以在编辑器中使用命令运行 安装路由,安装状态 选择插件 - 添加vue-router、添加vuex 安装…...
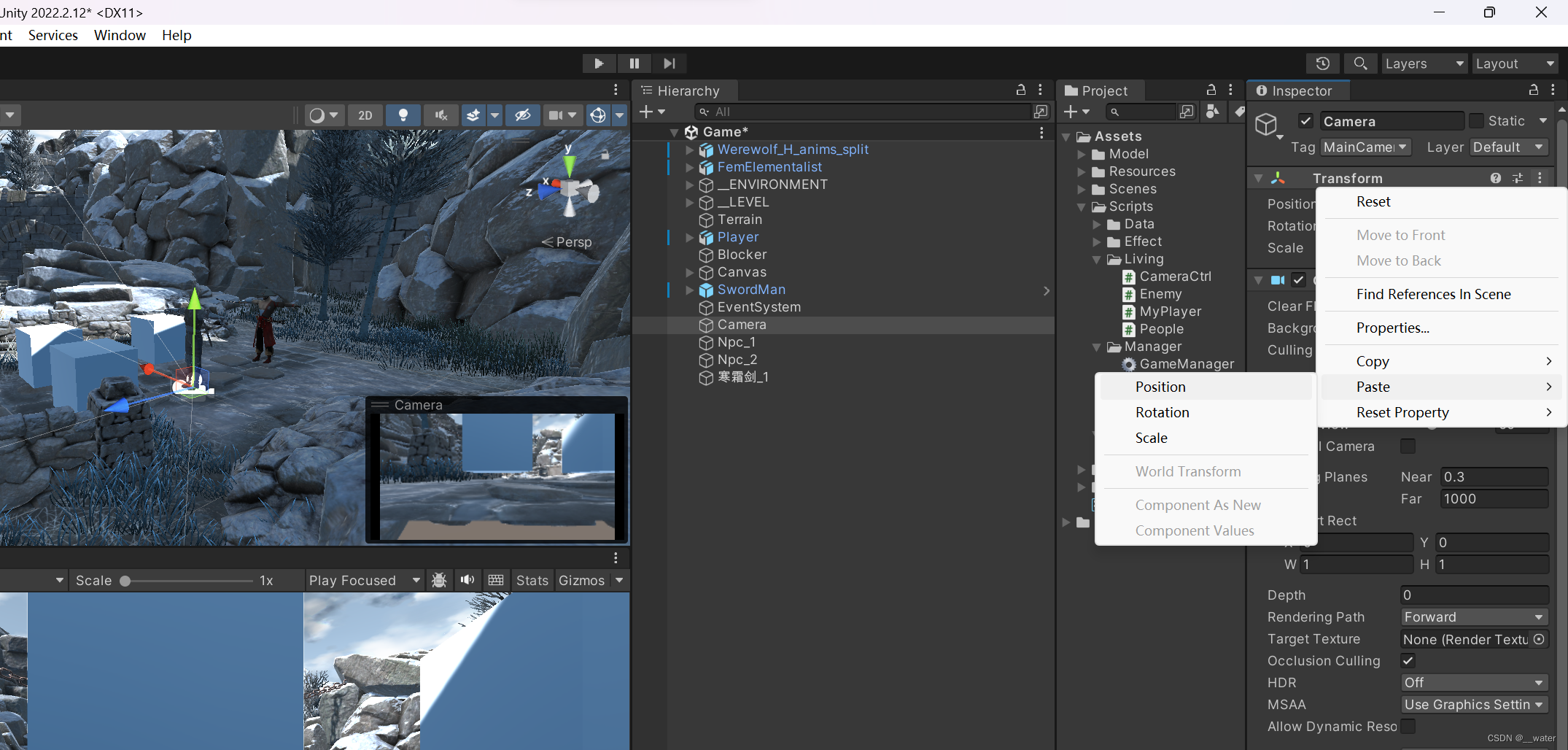
RPG项目01_脚本代码
基于“RPG项目01_场景及人物动画管理器”,我们创建一个XML文档 在资源文件夹下创建一个文件夹, 命名为Xml 将Xnl文档拖拽至文件夹中, 再在文件夹的Manager下新建脚本LoadManager 写代码: using System.Collections; using System…...

目标检测YOLO实战应用案例100讲-交通目标数据集构建及高性能检测算法研究与应用
目录 前言 国内外研究现状 目标检测研究现状 目标检测数据集研究现状...

浅谈Vue.js的计算属性computed
什么是computed属性 computed 属性用于声明计算属性,这些属性的值是基于其他响应式属性计算而来的,当依赖的响应式属性发生变化时,计算属性会自动重新计算。 与Vue.js 2相比,Vue.js 3的 computed 属性语法稍有变化,不…...

Linux常用指令详解
目录 前言: Linux的目录结构 Linux常用指令简介 whoami指令 ls指令 pwd指令 cd指令 tree指令 touch指令 mkdir指令 rmdir指令与rm指令 man指令 cp(copy)指令 mv(move)指令 cat指令 重定向及重定向的类型…...
)
Nginx(性能优化)
到这里文章的篇幅较长了,最后再来聊一下关于Nginx的性能优化,主要就简单说说收益最高的几个优化项,在这块就不再展开叙述了,毕竟影响性能都有多方面原因导致的,比如网络、服务器硬件、操作系统、后端服务、程序自身、数…...

机器学习笔记 - 如何在Python中对网格和点云进行体素化?
一、简述 本文主要是为了了解如何生成体素表示,体素之于3D就像像素之于2D。体素本质上是 3D 像素,但它们不是正方形,而是完美的立方体。 理论上,体素是复制现实的完美建模技术。 这里我们要了解四个广泛流行的 Python 库(Open3D、Trimesh、PyVista、pyntcloud )生成点云…...

冒个泡!OceanBase亮相 2023 新加坡金融科技节
近日,OceanBase 亮相 Singapore Fintech Festival 2023(2023 新加坡金融科技节)!本届新加坡金融科技节于 2023 年 11 月 15 日至 17 日在新加坡博览展览中心举行,展会期间,OceanBase 得到了众多金融科技机构…...
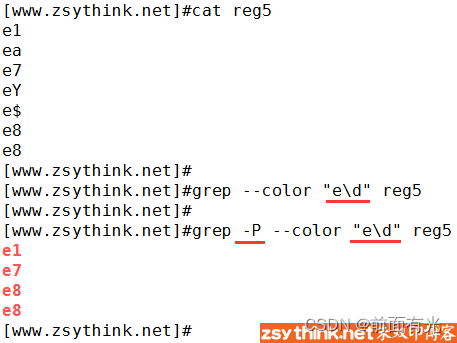
正则表达式(5):常用符号
正则表达式(5):常用符号 小结 本博文转载自 在本博客中,”正则表达式”为一系列文章,如果你想要从头学习怎样在Linux中使用正则,可以参考此系列文章,直达链接如下: 在Linux中使用正…...

Web安全漏洞分析-XSS(下)
随着互联网的迅猛发展,Web应用的普及程度也愈发广泛。然而,随之而来的是各种安全威胁的不断涌现,其中最为常见而危险的之一就是跨站脚本攻击(Cross-Site Scripting,简称XSS)。XSS攻击一直以来都是Web安全领…...
金南瓜SECS/GEM C# SDK 快速使用指南
本文对如何使用金南瓜SECS/GEM C# SDK 快速创建一个满足SECS/GEM通信要求的应用程序,只需简单3步完成。 第一步:创建C# .NET程序 示例使用Visual Studio 2010,使用者可以选择更高级版本 Visual Studio 第二步:添加DLL库引用&am…...

在一个没有超级用户的mongodb 生产库上如何添加超级用户
说来这个问题,都觉得不可思议,一个数据库怎么没有超级用户呢,我们知道,MYSQL,PG,ORACLE等,创建好后,都有一个默认的超级用户,MONGODB也有超级用户,但需要自己…...

排序算法之二:冒泡排序
冒泡排序的思路 冒泡排序是交换排序 基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动…...
一键搭建你的hnust请假条
hnust请假条 湖南科技大学请假条生成器 https://hnust.rick.icu/new (直接使用) Hnust Leave Note 去github https://github.com/rickhqh/hnust_leave_note 效果展示 界面展示效果图 v2.0 更新 vant和vue重构了整个源码同步学校新版请假条样式修复了…...
C练习题13
单项选择题(本大题共20小题,每小题2分,共40分。在每小题给出的四个备选项中,选出一个正确的答案,并将所选项前的字母填写在答题纸的相应位置上。) 1.结构化程序由三种基本结构组成、三种基本结构组成的算法是() A.可以完成任何复杂的任务 B. 只能完成部分复杂的任务 C. 只能完…...

交易历史记录20231206 记录
昨日回顾: select top 10000 * from dbo.CODEINFO A left join dbo.全部A股20231206010101 B ON A.CODE B.代码 left join dbo.全部A股20231206CONF D on A.CODED.代码left join dbo.全部A股20231206 G on A.CODEG.代码 left…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
