基于单片机的电子密码锁设计
1.设计任务
利用AT89C51单片机为核心控制元件,设计一个简易的电子密码锁,可设置四位密码,输入错误三次,报警灯亮起(红灯亮起),输入正确,绿灯闪烁三次。可通过LCD显示屏查看密码,并可通过特殊键位清除密码。
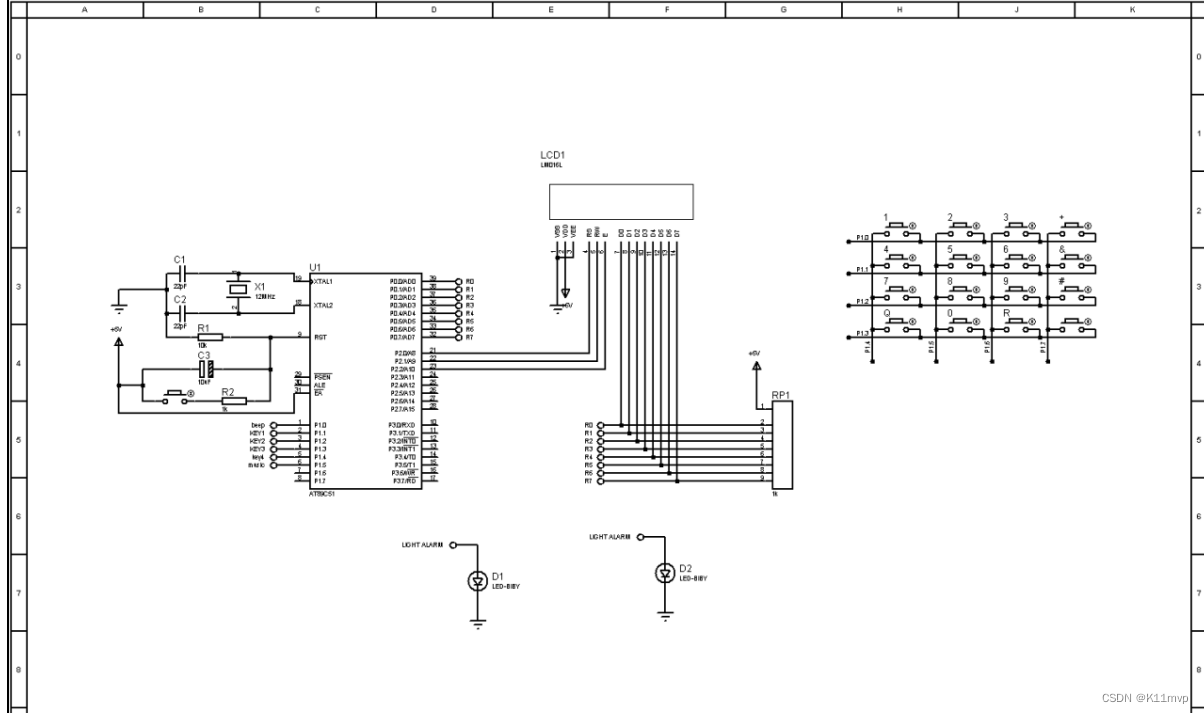
本系统由AT89C51单片机系统(主要是AT89C51单片机最小系统)、4X4矩阵键盘、LCD1602显示和报警系统等组成。
- 利用AT89C51单片机设计四位电子密码锁。
- 通过LCD显示查看已输入的密码。
- 可通过特殊按键清除密码。
- 密码输入正确后绿灯闪烁三次。
- 密码输错三次会有报警提示(报警红灯亮起)。
2. 设计要求
2.1系统方案论证
根据设计任务,分析设计系统的组成,给出实现设计任务的几种方案,分析比较几种设计方案的优略,本着尽量以软件代替硬件,同时力求电路简单,工作可靠的原则,确定总体设计方案。
2.2系统硬件电路设计
根据系统设计方案进行软、硬件的分配,软、硬件设计分别进行。硬件设计包括单片机最小系统和扩展接口及配置,硬件结构在设计时要选择合适的元器件,硬件电路要简洁、工作可靠,需用Proteus绘制整个系统的电路仿真原理图。
2.3软件设计
根据该系统要求的功能进行软件设计,简述软件的功能,并根据每个模块的功能绘制软件流程图,根据流程图编写程序并汇编调试通过;列出软件清单,软件清单要求加以注释。
#include <REGX52.H>
#include "Delay.h"
#include "LCD1602.h"
#include "MatrixKey.h"unsigned char N=0;
unsigned char KeyNum;
unsigned int Password,Count,Num_Val;sbit Led_G = P2^0;
sbit Led_R = P2^1;void main()
{Led_G = 1;Led_R = 1;LCD_Init();LCD_ShowString(1,1,"Password:");while(1){KeyNum=MatrixKey();if(KeyNum){if(KeyNum!=4&&KeyNum!=8&&KeyNum!=12&&KeyNum!=13&&KeyNum!=15&&KeyNum!=16) //如果S1~S10按键按下,输入密码{switch(KeyNum){case 1: Num_Val=1;break;case 2: Num_Val=2;break;case 3: Num_Val=3;break;case 5: Num_Val=4;break;case 6: Num_Val=5;break;case 7: Num_Val=6;break;case 9: Num_Val=7;break;case 10:Num_Val=8;break;case 11:Num_Val=9;break;case 14:Num_Val=0;break;}if(Count<4) //如果输入次数小于4{Password=Password*10; //密码左移一位Password=Password+Num_Val%10; //获取一位密码Count++; //计次加一}LCD_ShowNum(2,1,Password,4); //更新显示}if(KeyNum==15) //如果S11按键按下,确认{if(Password==2345) //如果密码等于正确密码{LCD_ShowString(1,14,"OK "); //显示OKLed_G = 0;Delay(300);Led_G = 1;Delay(300);Led_G = 0;Delay(300);Led_G = 1;Delay(300);Led_G = 0;Delay(300);Led_G = 1;Delay(300);Password=0; //密码清零Count=0; //计次清零LCD_ShowNum(2,1,Password,4); //更新显示LCD_ShowString(1,14," ");}else //否则{N++;if(N == 3){Led_R=0;Delay(2000);Led_R=1;N=0;}LCD_ShowString(1,14,"ERR"); //显示ERRPassword=0; //密码清零Count=0; //计次清零LCD_ShowNum(2,1,Password,4); //更新显示Delay(1000);LCD_ShowString(1,14," ");}}if(KeyNum==13) //如果S12按键按下,取消{Password=0; //密码清零Count=0; //计次清零LCD_ShowNum(2,1,Password,4); //更新显示}}}
}
完整代码点开链接私信获取。
【iBot机器人工作室的个人空间-哔哩哔哩】 https://b23.tv/ryUWVKa
相关文章:

基于单片机的电子密码锁设计
1.设计任务 利用AT89C51单片机为核心控制元件,设计一个简易的电子密码锁,可设置四位密码,输入错误三次,报警灯亮起(红灯亮起),输入正确,绿灯闪烁三次。可通过LCD显示屏查看密码&…...

ChatGPT学习笔记
1 ChatGPT架构图 (ChatGPT_Diagram.svg来自于【OpenA | Introducing ChatGPT】) 2 模型训练 ChatGPT在训练时使用了PPO方法;...
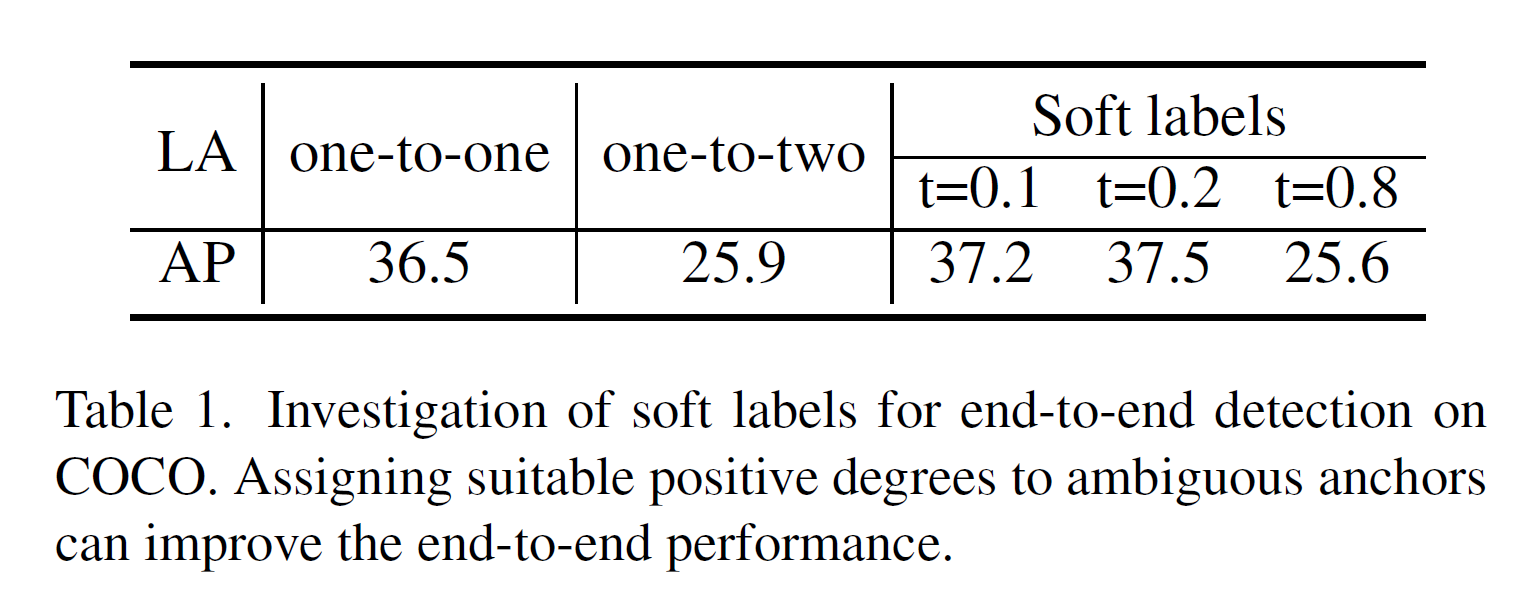
One-to-Few Label Assignment for End-to-End Dense Detection阅读笔记
One-to-Few Label Assignment for End-to-End Dense Detection阅读笔记 Abstract 一对一(o2o)标签分配对基于变换器的端到端检测起着关键作用,最近已经被引入到全卷积检测器中,用于端到端密集检测。然而,o2o可能因为…...

Ubuntu22.04 使用Docker部署Neo4j出错 Exited(70)
项目场景: 最近需要使用Neo4j图数据库,因此打算使用docker部署 环境使用WSL Ubuntu22.04 问题描述 拉下最新Neo4j镜像,执行命令部署 启动容器脚本 docker run -d -p 7474:7474 -p 7687:7687 \ --name neo4j \ --env "NEO4J_AUTHneo…...

【数据分析 | Numpy】Numpy模块系列指南(一),从设计架构说起
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...
多人聊天室
多人聊天包 由于要先创建服务面板,接收客户端连接的信息,此代码使用顺序为先启动服务端,在启动客户端,服务端不用关,不然会报错。多运行几次客户端,实现单人聊天 1.创建服务面板 package yiduiy;import j…...
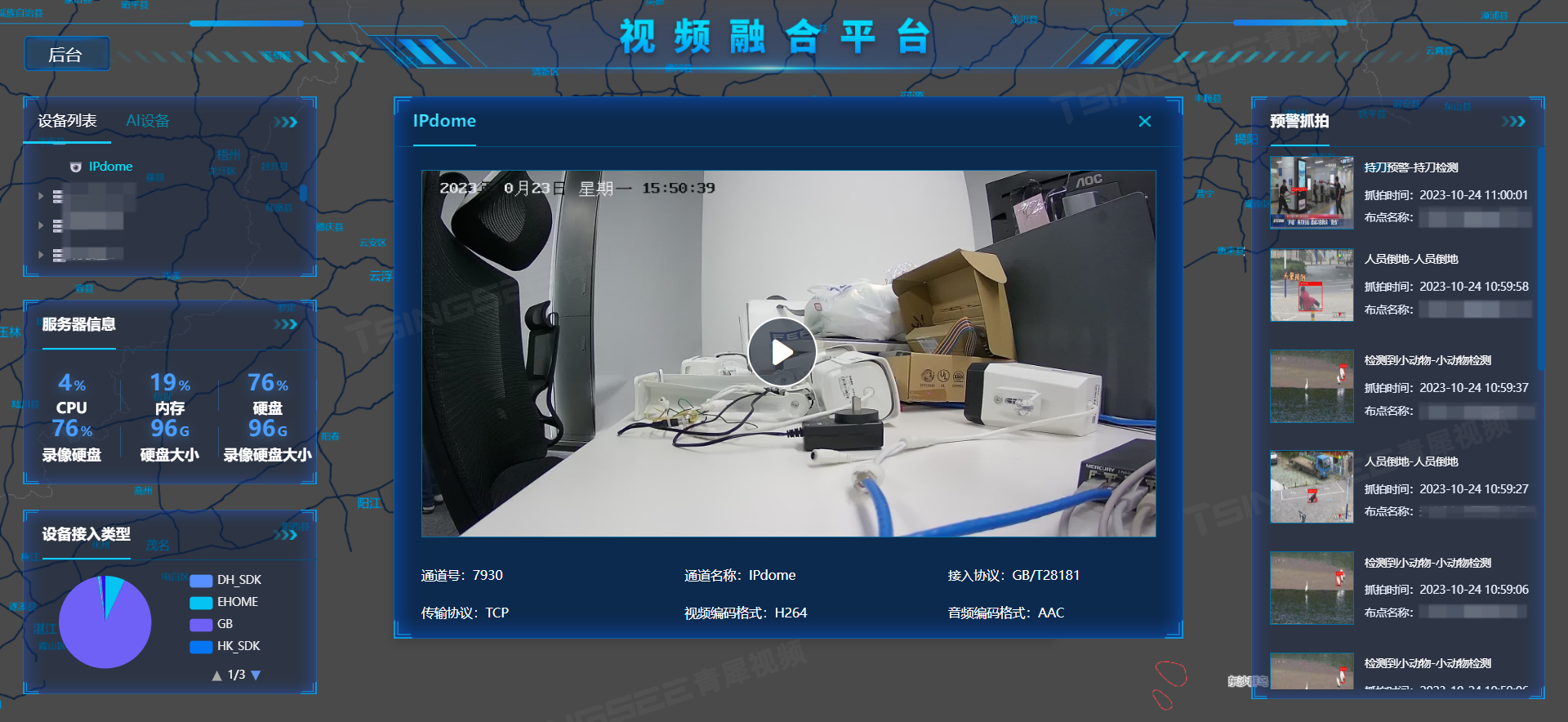
智慧园区可视化综合管理平台建设方案,智能化、数字化才是关键
园区作为城市的基本单元,是经济发展的重要载体。随着我国经济的快速发展,各类工业园区、办公园区等园区的规划建设也越来越多。伴随着互联网新兴技术的发展和应用,智慧园区已成为当今城市规划和社会发展的关注焦点,今天我们来介绍…...
kepler.gl部署在线说明文档
1 概述 1.1 介绍 1、Kepler.gl 是一个强大的开源地理空间分析工具,用于大规模数据集的可视化。它由 Uber 的数据可视化团队开发,并且是基于 Web 技术构建的。Kepler.gl 涉及到以下几个主要技术领域: WebGL: Kepler.gl 通过 WebGL 进行渲染…...

Java程序员,你掌握了多线程吗?
文章目录 01 多线程对于Java的意义02 为什么Java工程师必须掌握多线程03 Java多线程使用方式04 如何学好Java多线程写作末尾 摘要:互联网的每一个角落,无论是大型电商平台的秒杀活动,社交平台的实时消息推送,还是在线视频平台的流…...

Android 11.0 长按按键切换SIM卡默认移动数据
Android 11.0 长按按键切换SIM卡默认移动数据 近来收到客户需求想要通过长按按键实现切换SIM卡默认移动数据的功能,该功能主要通过长按按键发送广播来实现,具体修改参照如下: 首先创建广播,具体修改参照如下: /vend…...
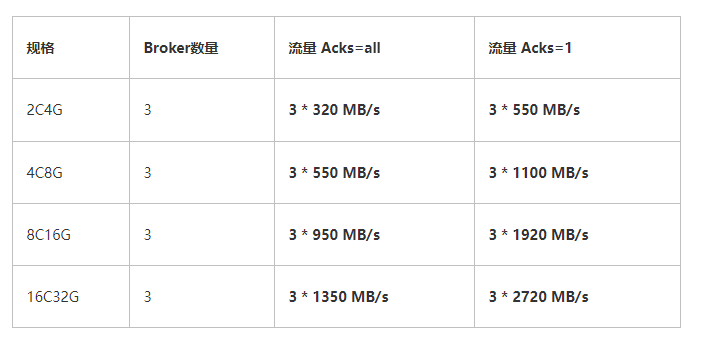
Kafka集群调优+能力探底
一、前言 我们需要对4个规格的kafka能力进行探底,即其可以承载的最大吞吐;4个规格对应的单节点的配置如下: 标准版: 2C4G 铂金版: 4C8G 专业版: 8C16G 企业版: 16C32G 另外,一般…...
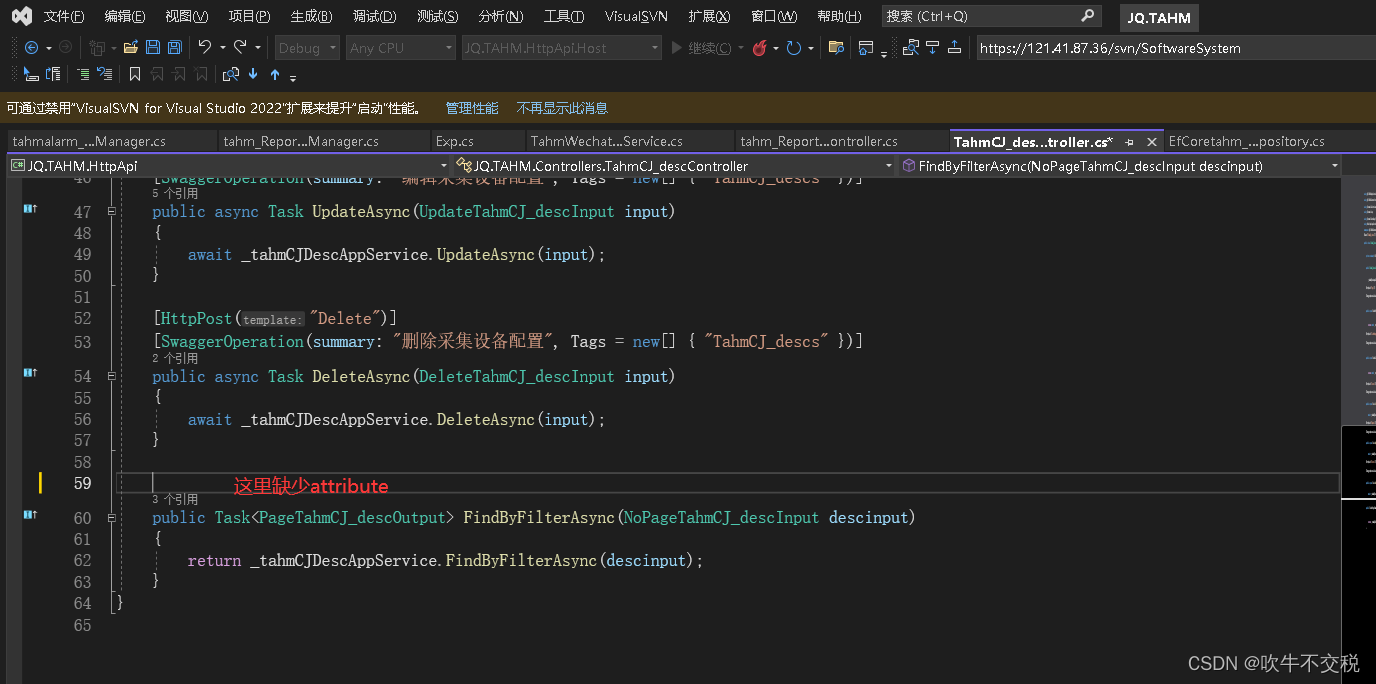
netcore swagger 错误 Failed to load API definition
后端接口报错如下: 前端nswag报错如下: 根据网上查询到的资料说明,说一般swagger这种错误都是控制器里有接口代码异常造成的,通常是接口没有加属性Attribute, 比如[HttpPost("Delete")]、[HttpGet("Del…...

UDP Socket API 的讲解,以及回显服务器客户端的实现
文章目录 UDPDatagramSocktet APIDatagramPacket API UDP 客户端服务器实现 UDP 先来认识一下 UDP 的 socket api,两个核心的类:DatagramSocket、DatagramPacket. DatagramSocktet API 是一个 socket 对象。 什么是 socket? 操作系统&…...
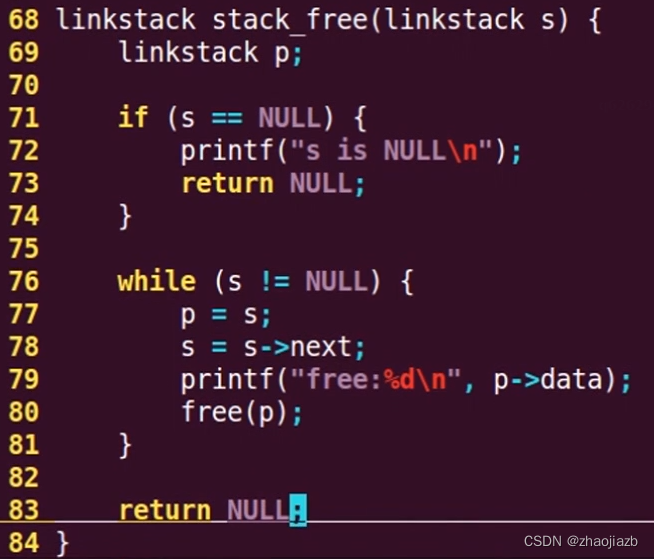
数据结构与算法-D7栈实现及应用
顺序栈 具有顺序表同样的存储结构,由数组定义,配合用数组下标表示的栈顶指针top完成操作 sqstack.h stack_creat stack_push stack_empty stack_full 1、判断栈是否为空 2、top--,取:data[top1] stack_top stack_clear stack_fre…...

蓝桥杯真题:分巧克力(二分法)-Java版
由题目可知,该题的最终结果具有单调性,边长越大,可分蛋糕越少 可以用二分模板的向右找: 整数二分 import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader;public class Main {static int n,k; //n个块蛋糕,k个学生static int N 10…...

c++面试题
1.static的使用 1)修饰局部变量:在函数内部使用static修饰局部变量,会使它成为静态局部变量。静态局部变量只会被初始化一次,且只有在第一次调用该函数时才会被初始化,之后每次调用该函数时都会保留上一次的值.从原来…...
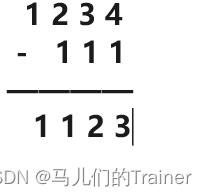
高精度加法,减法,乘法,除法(上)(C语言)
前言 加,减,乘,除这些运算我们自然信手捏来,就拿加法来说,我们要用c语言编程算ab的和,只需让sum ab即可,可是这是局限的,我们都知道int的表示的最大值为2147483647(32位…...

C++新经典模板与泛型编程:SFINAE特性的信息萃取
用成员函数重载实现is_default_constructible 首先介绍一个C标准库提供的可变参类模板std::is_default_constructible。这个类模板的主要功能是判断一个类的对象是否能被默认构造(所谓默认构造,就是构造一个类对象时,不需要给该类的构造函数…...
java单人聊天
服务端 package 单人聊天;import java.awt.BorderLayout; import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import java.io.BufferedReader; import java.io.InputStream; import java.io.InputStreamReader; import java.io.OutputStream; import…...

nodejs环境安装
node安装 wget https://mirrors.tuna.tsinghua.edu.cn/nodejs-release/v20.8.0/node-v20.8.0-linux-x64.tar.gz tar xf node-v20.8.0-linux-x64.tar.xz -C /usr/local/ ln -s node-v20.8.0-linux-x64 nodevim /etc/profile.d/node.sh export PATH$PATH:/usr/local/node/binnp…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
