12-07 周四 Pytorch 使用Visdom 进行可视化
简介
在完成了龙良曲的Pytroch视频课程之后,楼主对于pytroch有了进一步的理解,比如,比之前更加深刻的了解了BP神经网络的反向传播算法,梯度、损失、优化器这些名词更加熟悉。这个博客简要介绍一下在使用Pytorch进行数据可视化的一些内容。
安装
pip install visdom
启动服务
python -m visdom.server
使用
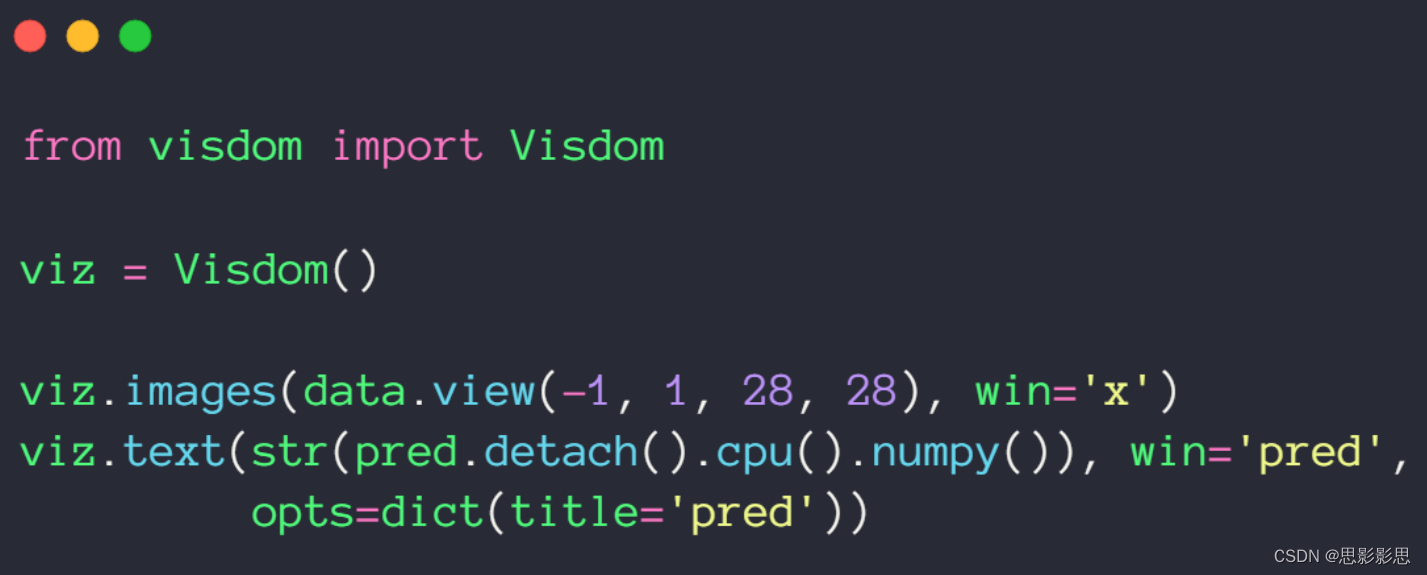
基本上是按照先生成对象,然后追加内容的方式。
import visdomvis = visdom.Visdom()
vis.line([0.], [0.], win='jax train-loss', name="train loss", opts=dict(title='jax train loss'))
vis.line([0.0], [0.], win='jax time-consumed', name="time", opts=dict(title='jax time'))
vis.text(f"jax 进行代理模型训练", win="jax log", opts={"title": "jax log"})# jit_train_step = train_step
start_time = time.time()
s1=start_time
for epoch in range(iterations):vis.text(f"{epoch+1}, Loss: {loss}, Time: {duration}", win="jax log", append=True)vis.line([loss.item()*1000], [epoch+1], win="jax train-loss", update='append', name="train loss", opts={"title": "jax train loss"})
vis.line([duration], [epoch+1], win='jax time-consumed', update='append', name="time", opts={"title": 'jax time'})

下图中,则是同一个图中同时绘制两个曲线
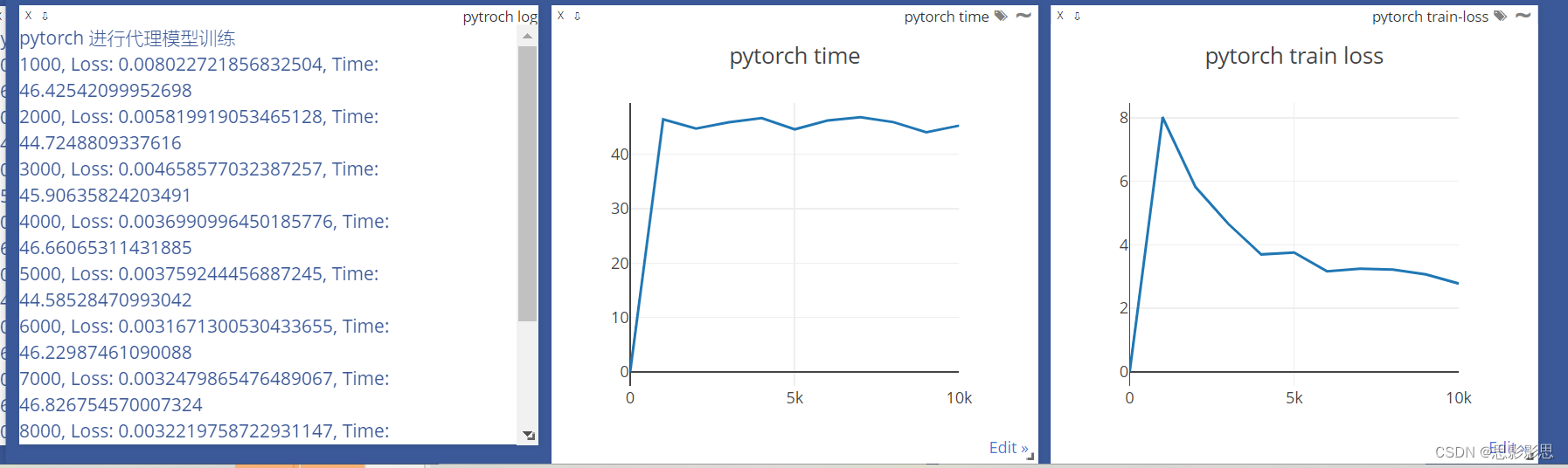
下图演示绘制曲线
呈现效果
相关文章:

12-07 周四 Pytorch 使用Visdom 进行可视化
简介 在完成了龙良曲的Pytroch视频课程之后,楼主对于pytroch有了进一步的理解,比如,比之前更加深刻的了解了BP神经网络的反向传播算法,梯度、损失、优化器这些名词更加熟悉。这个博客简要介绍一下在使用Pytorch进行数据可视化的一…...

基于微信小程序的智慧校园导航系统研究
点我下载完整版 基于微信小程序的智慧校园导航系统研究 Research on Smart Campus Navigation System based on WeChat mini program 目录 目录 2 摘要 3 关键词 4 第一章 研究背景与意义 4 1.1 校园导航系统研究的背景 4 1.2 微信小程序在校园导航系统中的应用 5 1.3 研究的目…...

VUE3给table的head添加popover筛选、时间去除时分秒、字符串替换某字符
1. VUE3给table的head添加popover筛选 <el-tableref"processTableRef"class"process-table"row-key"secuId":data"pagingData"style"width: 100%"highlight-current-row:height"stockListHeight":default-exp…...

19、XSS——HTTP协议安全
文章目录 一、Weak Session IDs(弱会话IDs)二、HTTP协议存在的安全问题三、HTTPS协议3.1 HTTP和HTTPS的区别3.2 SSL协议组成 一、Weak Session IDs(弱会话IDs) 当用户登录后,在服务器就会创建一个会话(Session),叫做会话控制&…...

深圳锐杰金融:用金融力量守护社区健康
深圳市锐杰金融投资有限公司,作为中国经济特区的中流砥柱,近年来以其杰出的金融成绩和坚定的社会责任立场引人注目。然而,这并非一个寻常的金融机构。锐杰金融正在用自己的方式诠释企业责任和慈善精神,通过一系列独特的慈善项目&a…...

python对py文件加密
参考文献: 【编程技巧】py文件批量编译,py批量转pyd,PyCharm设置py转pyd功能_py文件编译pyd-CSDN博客 【Python小技巧】加密又提速,把.py文件编译为.pyd文件(类似dll函数库),你值得拥有&#x…...
Thymeleaf生成pdf表格合并单元格描边不显示
生成pdf后左侧第一列的右描边不显示,但是html显示正常 显示异常时描边的写法 cellpadding“0” cellspacing“0” ,td,th描边 .self-table{border:1px solid #000;border-collapse: collapse;width:100%}.self-table th{font-size:12px;border:1px sol…...
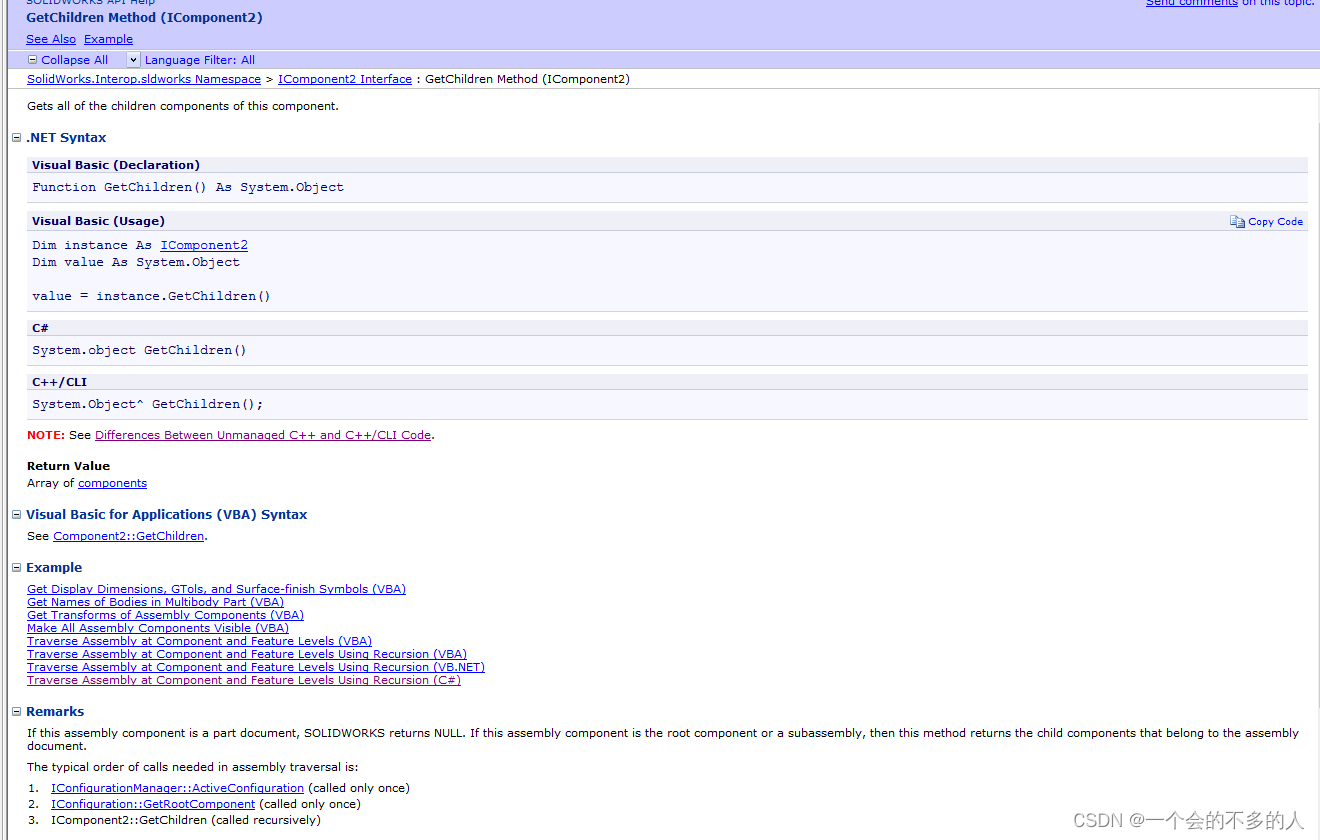
C# Solidworks二次开发:三种获取SW设计结构树的方法-第二讲
今天这篇文章是接上一篇文章的,主要讲述的是获取SW设计结构树节点的第二种方法。 这个方法获取节点的逻辑是先获取最顶层节点,然后再通过获取顶层节点的子节点一层一层的把所有节点都找出来,也就是需要递归。想要用这个方法就要了解下面几个…...
分布式搜索引擎03
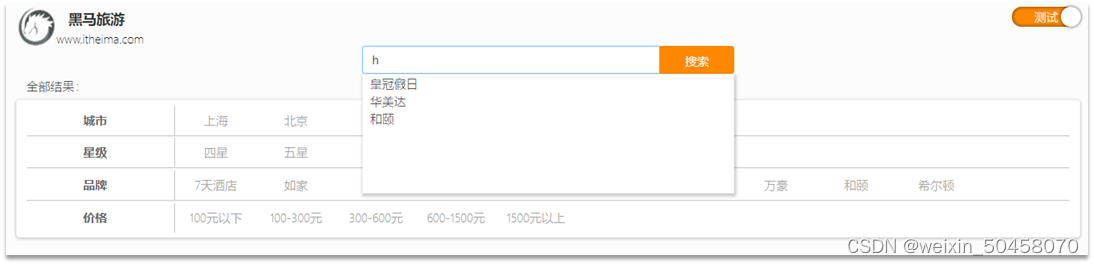
1.数据聚合 聚合(aggregations)可以让我们极其方便的实现对数据的统计、分析、运算。例如: 什么品牌的手机最受欢迎? 这些手机的平均价格、最高价格、最低价格? 这些手机每月的销售情况如何? 实现这些统计功能的比数据库的sql要方便的多,而且查询速度非常快,可以实现近…...
flex布局的flex为1到底是什么
参考博客:flex:1什么意思_公孙元二的博客-CSDN博客 flex:1即为flex-grow:1,经常用作自适应布局,将父容器的display:flex,侧边栏大小固定后,将内容区flex:1,内…...

class050 双指针技巧与相关题目【算法】
class050 双指针技巧与相关题目【算法】 算法讲解050【必备】双指针技巧与相关题目 code1 922. 按奇偶排序数组 II // 按奇偶排序数组II // 给定一个非负整数数组 nums。nums 中一半整数是奇数 ,一半整数是偶数 // 对数组进行排序,以便当 nums[i] 为…...

计算机操作系统4
1.什么是进程同步 2.什么是进程互斥 3.进程互斥的实现方法(软件) 4.进程互斥的实现方法(硬件) 5.遵循原则 6.总结: 线程是一个基本的cpu执行单元,也是程序执行流的最小单位。 调度算法:先来先服务FCFS、短作业优先、高响应比优先、时间片…...

【ASP.NET CORE】EntityFrameworkCore 数据迁移
如果数据库中已经有数据结构,可以使用Scaffold-DbContext来同步model,-connection是字符串,-outputdir 是输入文件夹名称,举例的脚本使用的是sqlserver数据库 通用 Scaffold-DbContext -Connection "DatabaseAddress;Data …...

说说React jsx转换成真实DOM的过程?
在React中,JSX(JavaScript XML)是一种语法糖,用于描述用户界面的结构和组件关系。当你编写React组件并包含JS JSX解析:React中的JSX代码首先会被解析成JavaScript对象。这个过程通常是通过Babel等工具进行的࿰…...
MongoDB知识总结
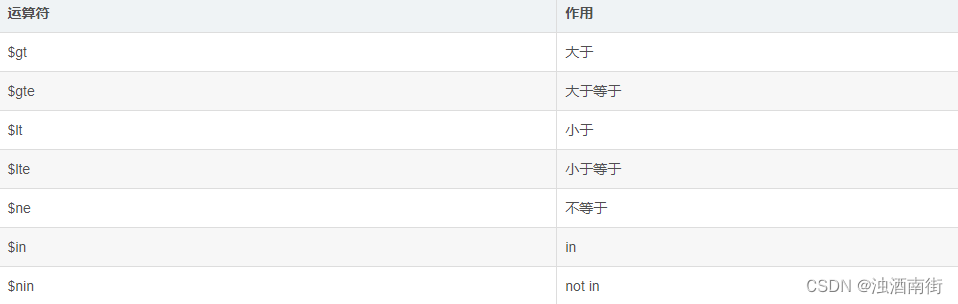
这里写自定义目录标题 MongoDB基本介绍MongoDB基本操作数据库相关集合相关增删改查 MongoDB基本介绍 简单介绍 MongoDB是一个基于分布式文件存储的数据库。由C语言编写。旨在为WEB应用提供可扩展的高性能数据存储解决方案。 MongoDB是一个介于关系数据库和非关系数据库之间的产…...

【LeeCode】1.两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按任意顺序返回…...

Python 作业答疑_6.15~6.18
一、Python 一班 1. 比较字符串 1.1 问题描述 比较两个字符串A和B,字符串A和B中的字符都是大写字母,确定A中是否包含B中所有的字符。 1.2 问题示例 例如,给出A"ABCD",B"ACD",返回True&#x…...

Diffusion 公式推导
Diffusion:通过扩散和逆扩散过程生成图像的生成式模型 中已经对 diffusion 的原理进行了直观地梳理,本文对其中的数学推导进行讲解,还是基于 DDPM。 目录 一. 预备知识1. 重参数技巧2. 高斯分布的可加性3. 扩散递推式的由来 二. 扩散过程1. 背…...

【C语言快速学习基础篇】之一基础类型、进制转换、数据位宽
文章目录 一、基础类型(根据系统不同占用字节数会有变化)1.1、有符号整形1.2、无符号整形1.3、字符型1.4、浮点型1.5、布尔型 二、进制转换2.1、二进制2.2、八进制2.3、十进制2.4、十六进制2.5、N进制2.6、进制转换关系对应表 三、数据位宽3.1、位3.2、字节3.3、字3.4、双字3.5…...
使用GPT-4V解决Pycharm设置问题
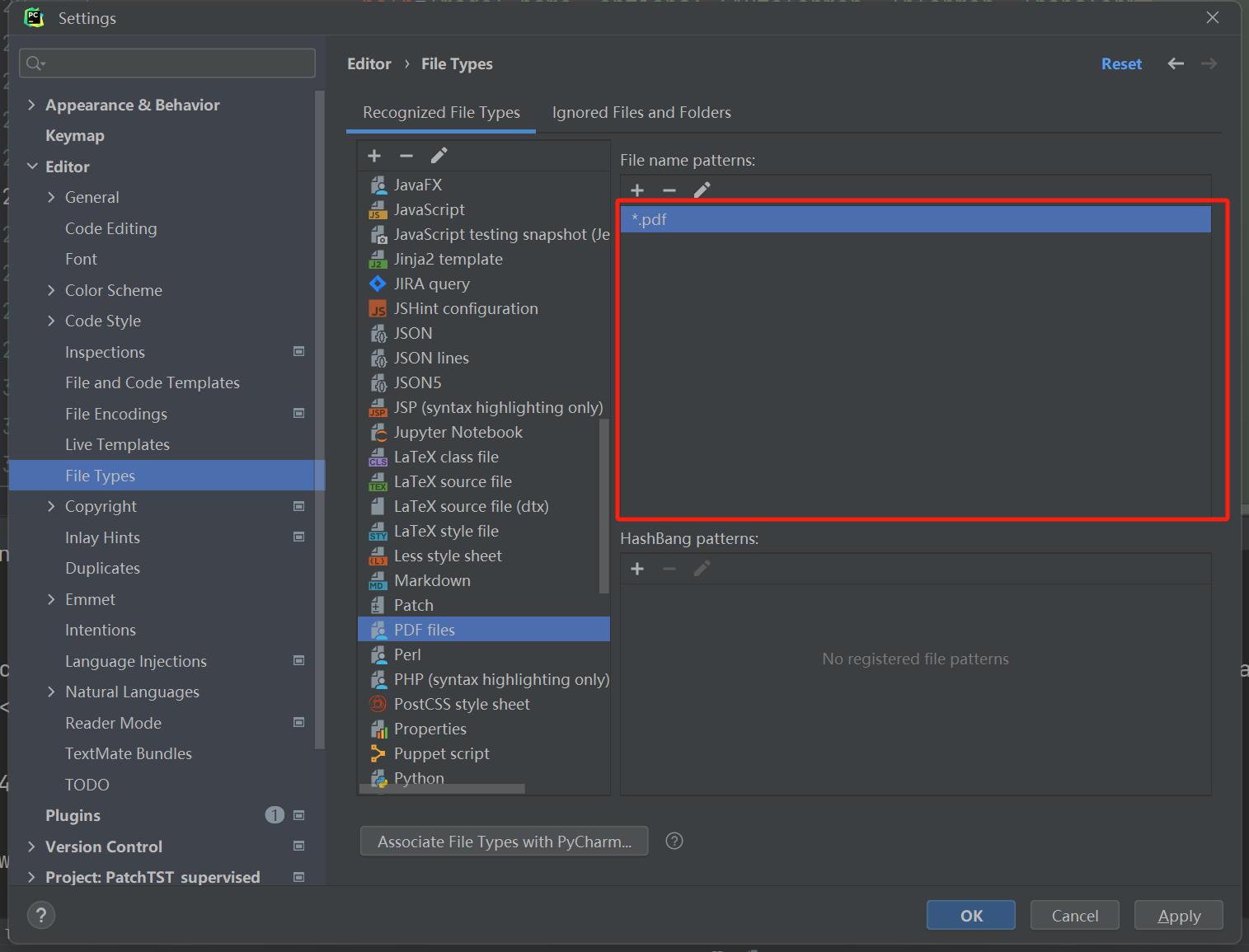
pycharm如何实现关联,用中文回答 在PyCharm中关联PDF文件类型,您可以按照以下步骤操作: 1. 打开PyCharm设置:点击菜单栏中的“File”(文件),然后选择“Settings”(设置)。…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...