Diffusion 公式推导
Diffusion:通过扩散和逆扩散过程生成图像的生成式模型 中已经对 diffusion 的原理进行了直观地梳理,本文对其中的数学推导进行讲解,还是基于 DDPM。
目录
- 一. 预备知识
- 1. 重参数技巧
- 2. 高斯分布的可加性
- 3. 扩散递推式的由来
- 二. 扩散过程
- 1. 背景声明
- 2. 公式推导
- 三. 逆扩散过程
- 1. 背景声明
- 2. 公式推导
- 四. 训练过程
一. 预备知识
1. 重参数技巧
重参数技巧 (Reparametrization Trick) 是一种在深度学习中用于训练概率模型的技术,通常用于变分推断和概率生成模型,如变分自动编码器 (Variational Autoencoders, VAE)。这些模型的部分参数是使用特定概率分布随机采样得到的而不是确定性的值,在梯度下降反向优化时难以计算。
因此引入了重参数技巧,通过重新引入可微变换来参数化随机变量,将采样操作转换为模型参数和一个固定的噪声项的函数,使得梯度计算变得可行。举个例子 1,如果要从高斯分布 z ∼ N ( z ; μ θ , σ θ 2 I ) z \sim \mathcal{N}\left(z ; \mu_\theta, \sigma_\theta^2 \mathbf{I}\right) z∼N(z;μθ,σθ2I) 中采样一个 z z z,可以写成:
z = μ θ + σ θ ⊙ ϵ , ϵ ∼ N ( 0 , I ) z=\mu_\theta+\sigma_\theta \odot \epsilon, \epsilon \sim \mathcal{N}(0, \mathbf{I}) z=μθ+σθ⊙ϵ,ϵ∼N(0,I)
其中, μ θ \mu_\theta μθ 表示分布的均值, σ θ \sigma_\theta σθ 表示分布的标准差, ⊙ \odot ⊙ 表示对矩阵的逐元素相乘, ϵ \epsilon ϵ 是从标准高斯分布中采样的噪声项。这样,我们可以对 μ θ \mu_\theta μθ 和 σ θ \sigma_\theta σθ 进行梯度计算,而不需要对采样操作进行梯度计算。
重参数技巧的使用可以使得概率模型的训练更加高效和稳定。
2. 高斯分布的可加性
两个互相独立的高斯分布之和仍为高斯分布,即:
X 1 ∼ N ( μ 1 , σ 1 2 ) X 2 ∼ N ( μ 2 , σ 2 2 ) X_1 \sim N(\mu_1, \sigma_1^2)\\X_2 \sim N(\mu_2, \sigma_2^2) X1∼N(μ1,σ12)X2∼N(μ2,σ22)
则:
X 1 + X 2 ∼ N ( μ 1 + μ 2 , σ 1 2 + σ 2 2 ) X 1 − X 2 ∼ N ( μ 1 − μ 2 , σ 1 2 + σ 2 2 ) X_1+X_2 \sim N(\mu_1+\mu_2, \sigma_1^2+\sigma_2^2)\\X_1-X_2 \sim N(\mu_1-\mu_2, \sigma_1^2+\sigma_2^2) X1+X2∼N(μ1+μ2,σ12+σ22)X1−X2∼N(μ1−μ2,σ12+σ22)
两个高斯分布的和本质上就是二维连续型随机变量函数的分布,可以通过计算其概率密度函数证明,见 证明两个互相独立的高斯分布之和仍为高斯分布。
3. 扩散递推式的由来
不知道有多少读者和我一样,阅读 DDPM 时对扩散的递推式 q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(x_t \mid x_{t-1})=\mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t \bold I) q(xt∣xt−1)=N(xt;1−βtxt−1,βtI) 感到疑惑,文中也没有解释这是怎么来的,网上的很多公式讲解也都是直接引用了该式进行推导。本节参考 一文解释 Diffusion Model (一) DDPM 理论推导,对扩散过程的递推式的由来进行梳理。2
基于 diffusion 的原理,扩散过程是一个不断加噪的过程,因此相邻图像应该满足线性关系,且图像信息应当被不断减弱,形如:
x t = a t x t − 1 + b t ε t , ε t ∼ N ( 0 , I ) \boldsymbol{x}_t=a_t \boldsymbol{x}_{t-1}+b_t \boldsymbol{\varepsilon}_t, \quad \boldsymbol{\varepsilon}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \\ xt=atxt−1+btεt,εt∼N(0,I)
因为 x t \boldsymbol{x}_t xt 中包含的图像信息相较 x t − 1 \boldsymbol{x}_{t-1} xt−1 更少,因此衰减系数 0 < a t < 1 0<a_t<1 0<at<1。同样,噪声系数 0 < b t < 1 0<b_t<1 0<bt<1。
将 x t − 1 \boldsymbol{x}_{t-1} xt−1 代入 x t \boldsymbol{x}_t xt 可以得到:
x t = a t x t − 1 + b t ε t = a t ( a t − 1 x t − 2 + b t − 1 ε t − 1 ) + b t ε t = a t a t − 1 x t − 2 + a t b t − 1 ε t − 1 + b t ε t = … = ( a t … a 1 ) x 0 + ( a t … a 2 ) b 1 ε 1 + ( a t … a 3 ) b 2 ε 2 + ⋯ + a t b t − 1 ε t − 1 + b t ε t \begin{aligned} \boldsymbol{x}_t & =a_t \boldsymbol{x}_{t-1}+b_t \boldsymbol{\varepsilon}_t \\ & =a_t\left(a_{t-1} \boldsymbol{x}_{t-2}+b_{t-1} \varepsilon_{t-1}\right)+b_t \varepsilon_t \\ & =a_t a_{t-1} \boldsymbol{x}_{t-2}+a_t b_{t-1} \boldsymbol{\varepsilon}_{t-1}+b_t \boldsymbol{\varepsilon}_t \\ & =\ldots \\ & =\left(a_t \ldots a_1\right) \boldsymbol{x}_0+\left(a_t \ldots a_2\right) b_1 \varepsilon_1+\left(a_t \ldots a_3\right) b_2 \varepsilon_2+\cdots+a_t b_{t-1} \varepsilon_{t-1}+b_t \varepsilon_t \\ \end{aligned} xt=atxt−1+btεt=at(at−1xt−2+bt−1εt−1)+btεt=atat−1xt−2+atbt−1εt−1+btεt=…=(at…a1)x0+(at…a2)b1ε1+(at…a3)b2ε2+⋯+atbt−1εt−1+btεt
x t \boldsymbol{x}_t xt 的第一项关于原始图像 x 0 \boldsymbol{x}_0 x0,其余余项可以利用高斯分布的可加性进行整合,满足高斯分布 N ( 0 , ( ( a t … a 2 ) 2 b 1 2 + ( a t … a 3 ) 2 b 2 2 + ⋯ + a t 2 b t − 1 2 + b t 2 ) I ) \mathcal{N}(\mathbf{0}, (\left(a_t \ldots a_2\right)^2 b_1^2+\left(a_t \ldots a_3\right)^2 b_2^2+\cdots+a_t^2 b_{t-1}^2+b_t^2)\mathbf{I}) N(0,((at…a2)2b12+(at…a3)2b22+⋯+at2bt−12+bt2)I)。于是可以将 x t \boldsymbol{x}_t xt 写成:
x t = ( a t … a 1 ) x 0 + ( a t … a 2 ) b 1 ε 1 + ( a t … a 3 ) b 2 ε 2 + ⋯ + a t b t − 1 ε t − 1 + b t ε t = ( a t … a 1 ) x 0 + ( a t … a 2 ) 2 b 1 2 + ( a t … a 3 ) 2 b 2 2 + ⋯ + a t 2 b t − 1 2 + b t 2 ε ‾ t , \begin{aligned} \boldsymbol{x}_t & =\left(a_t \ldots a_1\right) \boldsymbol{x}_0+\left(a_t \ldots a_2\right) b_1 \varepsilon_1+\left(a_t \ldots a_3\right) b_2 \varepsilon_2+\cdots+a_t b_{t-1} \varepsilon_{t-1}+b_t \varepsilon_t \\ & =\left(a_t \ldots a_1\right) \boldsymbol{x}_0+\sqrt{\left(a_t \ldots a_2\right)^2 b_1^2+\left(a_t \ldots a_3\right)^2 b_2^2+\cdots+a_t^2 b_{t-1}^2+b_t^2} \overline{\boldsymbol{\varepsilon}}_t, \\ \end{aligned} xt=(at…a1)x0+(at…a2)b1ε1+(at…a3)b2ε2+⋯+atbt−1εt−1+btεt=(at…a1)x0+(at…a2)2b12+(at…a3)2b22+⋯+at2bt−12+bt2εt,
其中 ε ‾ t ∼ N ( 0 , I ) \overline{\varepsilon}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) εt∼N(0,I),服从标准高斯分布。
接下来再看 ε ‾ t \overline{\varepsilon}_t εt 前面的系数,为了一般性表示,在前面添加 ( a t … a 1 ) 2 \left(a_t \ldots a_1\right)^2 (at…a1)2 项,最后再减去即可:
( a t … a 1 ) 2 + ( a t … a 2 ) 2 b 1 2 + ( a t … a 3 ) 2 b 2 2 + ⋯ + a t 2 b t − 1 2 + b t 2 − ( a t … a 1 ) 2 = ( a t … a 2 ) 2 a 1 2 + ( a t … a 2 ) 2 b 1 2 + ( a t … a 3 ) 2 b 2 2 + ⋯ + a t 2 b t − 1 2 + b t 2 − ( a t … a 1 ) 2 = ( a t … a 2 ) 2 ( a 1 2 + b 1 2 ) + ( a t … a 3 ) 2 b 2 2 + ⋯ + a t 2 b t − 1 2 + b t 2 − ( a t … a 1 ) 2 = ( a t … a 3 ) 2 ( a 2 2 ( a 1 2 + b 1 2 ) + b 2 2 ) + ⋯ + a t 2 b t − 1 2 + b t 2 − ( a t … a 1 ) 2 = a t 2 ( a t − 1 2 ( … ( a 2 2 ( a 1 2 + b 1 2 ) + b 2 2 ) + … ) + b t − 1 2 ) + b t 2 − ( a t … a 1 ) 2 \begin{aligned} & \left(a_t \ldots a_1\right)^2+\left(a_t \ldots a_2\right)^2 b_1^2+\left(a_t \ldots a_3\right)^2 b_2^2+\cdots+a_t^2 b_{t-1}^2+b_t^2 - \left(a_t \ldots a_1\right)^2\\ =& \left(a_t \ldots a_2\right)^2 a_1^2+\left(a_t \ldots a_2\right)^2 b_1^2+\left(a_t \ldots a_3\right)^2 b_2^2+\cdots+a_t^2 b_{t-1}^2+b_t^2 - \left(a_t \ldots a_1\right)^2\\ =& \left(a_t \ldots a_2\right)^2\left(a_1^2+b_1^2\right)+\left(a_t \ldots a_3\right)^2 b_2^2+\cdots+a_t^2 b_{t-1}^2+b_t^2 - \left(a_t \ldots a_1\right)^2\\ =& \left(a_t \ldots a_3\right)^2\left(a_2^2\left(a_1^2+b_1^2\right)+b_2^2\right)+\cdots+a_t^2 b_{t-1}^2+b_t^2 - \left(a_t \ldots a_1\right)^2\\ =& a_t^2\left(a_{t-1}^2\left(\ldots\left(a_2^2\left(a_1^2+b_1^2\right)+b_2^2\right)+\ldots\right)+b_{t-1}^2\right)+b_t^2 - \left(a_t \ldots a_1\right)^2\\ \end{aligned} ====(at…a1)2+(at…a2)2b12+(at…a3)2b22+⋯+at2bt−12+bt2−(at…a1)2(at…a2)2a12+(at…a2)2b12+(at…a3)2b22+⋯+at2bt−12+bt2−(at…a1)2(at…a2)2(a12+b12)+(at…a3)2b22+⋯+at2bt−12+bt2−(at…a1)2(at…a3)2(a22(a12+b12)+b22)+⋯+at2bt−12+bt2−(at…a1)2at2(at−12(…(a22(a12+b12)+b22)+…)+bt−12)+bt2−(at…a1)2
为了表示的简洁以及便于书写,加一个限制条件: a i 2 + b i 2 = 1 a_i^2+b_i^2=1 ai2+bi2=1,就可以将 x t \boldsymbol{x}_t xt 大大简化:
x t = ( a t … a 1 ) x 0 + ( a t … a 2 ) 2 b 1 2 + ( a t … a 3 ) 2 b 2 2 + ⋯ + a t 2 b t − 1 2 + b t 2 ε ‾ t , = ( a t … a 1 ) x 0 + 1 − ( a t … a 1 ) 2 ε ‾ t \begin{aligned} \boldsymbol{x}_t & =\left(a_t \ldots a_1\right) \boldsymbol{x}_0+\sqrt{\left(a_t \ldots a_2\right)^2 b_1^2+\left(a_t \ldots a_3\right)^2 b_2^2+\cdots+a_t^2 b_{t-1}^2+b_t^2} \overline{\boldsymbol{\varepsilon}}_t, \\ & = \left(a_t \ldots a_1\right) \boldsymbol{x}_0 + \sqrt{1-\left(a_t \ldots a_1\right)^2} \overline{\boldsymbol{\varepsilon}}_t \end{aligned} xt=(at…a1)x0+(at…a2)2b12+(at…a3)2b22+⋯+at2bt−12+bt2εt,=(at…a1)x0+1−(at…a1)2εt
记 α ‾ t = ( a t … a 1 ) 2 \overline{\alpha}_t = \left(a_t \ldots a_1\right)^2 αt=(at…a1)2,则有:
x t = α ‾ t x 0 + 1 − α ‾ t ε ‾ t , ε ‾ t ∼ N ( 0 , I ) \boldsymbol{x}_t=\sqrt{\overline{\alpha}_t} \boldsymbol{x}_0+\sqrt{1-\overline{\alpha}_t} \overline{\varepsilon}_t, \quad \overline{\varepsilon}_t \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) xt=αtx0+1−αtεt,εt∼N(0,I)
上式和(7)式相同。
二. 扩散过程
1. 背景声明
-
记原始图像为 x 0 x_0 x0,扩散过程累计 T T T 次对其添加高斯噪声,得到 x 1 , x 2 , … , x T x_1, x_2, \dots, x_T x1,x2,…,xT;
-
记 x t ∼ q ( x t ) x_t \sim q(x_t) xt∼q(xt),表示其服从的概率分布而不是一个具体的特定值;
-
根据 diffusion 模型的原理, x T ∼ N ( 0 , I ) x_T \sim \mathcal{N}(0, \bold I) xT∼N(0,I),其中 I \bold I I 为单位矩阵;
-
扩散过程添加的噪声都满足均值为 0 的高斯分布,方差是超参数,用来调整扩散效果。引入方差系数为 β 1 , β 2 , … , β T , β t ∈ ( 0 , 1 ) \beta_1, \beta_2, \dots, \beta_T, \beta_t \in (0,1) β1,β2,…,βT,βt∈(0,1),具体实现是从 0.0001 到 0.02 线性插值。文中定义扩散过程如下:
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) (1) q(x_t \mid x_{t-1})=\mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t \bold I) \tag{1} q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)(1) -
因为扩散过程是马尔科夫过程,因此有:
q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) (2) q(x_{1:T} \mid x_{0})=\prod_{t=1}^T q(x_t \mid x_{t-1}) \tag{2} q(x1:T∣x0)=t=1∏Tq(xt∣xt−1)(2)直观来讲, x t x_t xt 在 x t − 1 x_{t-1} xt−1 的基础上乘上系数 1 − β t \sqrt{1-\beta_t} 1−βt,相当于一个变淡的过程;再加上扰动 β t ϵ t − 1 \beta_t \epsilon_{t-1} βtϵt−1,就能够让图像向标准高斯分布靠近。
-
为了表示方便,记 α t = 1 − β t \alpha_t = 1- \beta_t αt=1−βt, α ‾ t = ∏ i = 1 t α i \overline{\alpha}_t = \prod_{i=1}^t \alpha_i αt=∏i=1tαi;
2. 公式推导
将(1)式使用重参化技巧表示:
x t = 1 − β t x t − 1 + β t ϵ t − 1 其中 ϵ t − 1 ∼ N ( 0 , I ) (3) x_t = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t} \epsilon_{t-1} \quad \text{ 其中 }\epsilon_{t-1} \sim \mathcal{N}(0, \bold I) \tag{3} xt=1−βtxt−1+βtϵt−1 其中 ϵt−1∼N(0,I)(3)
将 x t − 1 x_{t-1} xt−1 代入 x t x_{t} xt 得到:
∵ x t = 1 − β t x t − 1 + β t ϵ t − 1 x t − 1 = 1 − β t − 1 x t − 2 + β t − 1 ϵ t − 2 ∴ x t = 1 − β t ( 1 − β t − 1 x t − 2 + β t − 1 ϵ t − 2 ) + β t ϵ t − 1 = ( 1 − β t ) ( 1 − β t − 1 ) x t − 2 + ( 1 − β t ) β t − 1 ϵ t − 2 + β t ϵ t − 1 = α t α t − 1 x t − 2 + α t ( 1 − α t − 1 ) ϵ t − 2 + 1 − α t ϵ t − 1 (4) \because \quad x_t = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t} \epsilon_{t-1}\\ \quad\quad x_{t-1} = \sqrt{1-\beta_{t-1}}x_{t-2} + \sqrt{\beta_{t-1}} \epsilon_{t-2}\\ \begin{aligned} \therefore \quad x_t & = \sqrt{1-\beta_t}(\sqrt{1-\beta_{t-1}}x_{t-2} + \sqrt{\beta_{t-1}} \epsilon_{t-2}) + \sqrt{\beta_t} \epsilon_{t-1}\\ & = \sqrt{(1-\beta_t)(1-\beta_{t-1})} x_{t-2} + \sqrt{(1-\beta_t)\beta_{t-1}} \epsilon_{t-2} + \sqrt{\beta_t} \epsilon_{t-1}\\ & = \sqrt{\alpha_t\alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t(1-\alpha_{t-1})} \epsilon_{t-2} + \sqrt{1-\alpha_{t}} \epsilon_{t-1} \tag{4} \end{aligned} ∵xt=1−βtxt−1+βtϵt−1xt−1=1−βt−1xt−2+βt−1ϵt−2∴xt=1−βt(1−βt−1xt−2+βt−1ϵt−2)+βtϵt−1=(1−βt)(1−βt−1)xt−2+(1−βt)βt−1ϵt−2+βtϵt−1=αtαt−1xt−2+αt(1−αt−1)ϵt−2+1−αtϵt−1(4)
如果 ϵ t \epsilon_{t} ϵt 是特定值,后面的余项就不能继续处理。但 ϵ t \epsilon_{t} ϵt 是重参化过程中引入的标准高斯分布中采样,结合高斯分布的可加性,有:
∵ α t ( 1 − α t − 1 ) ϵ t − 2 ∼ N ( 0 , α t ( 1 − α t − 1 ) I ) 1 − α t ϵ t − 1 ∼ N ( 0 , ( 1 − α t ) I ) ∴ α t ( 1 − α t − 1 ) ϵ t − 2 + 1 − α t ϵ t − 1 ∼ N ( 0 , ( 1 − α t α t − 1 ) I ) \because \quad \sqrt{\alpha_t(1-\alpha_{t-1})} \epsilon_{t-2} \sim \mathcal{N}(0, \alpha_t(1-\alpha_{t-1})\bold I)\\ \sqrt{1-\alpha_{t}} \epsilon_{t-1} \sim \mathcal{N}(0, (1-\alpha_{t}) \bold I)\\ \therefore \quad \sqrt{\alpha_t(1-\alpha_{t-1})} \epsilon_{t-2} + \sqrt{1-\alpha_{t}} \epsilon_{t-1} \sim \mathcal{N}(0, (1-\alpha_t\alpha_{t-1})\bold I) ∵αt(1−αt−1)ϵt−2∼N(0,αt(1−αt−1)I)1−αtϵt−1∼N(0,(1−αt)I)∴αt(1−αt−1)ϵt−2+1−αtϵt−1∼N(0,(1−αtαt−1)I)
因此可以将余项合并,改写成:
α t ( 1 − α t − 1 ) ϵ t − 2 + 1 − α t ϵ t − 1 = 1 − α t α t − 1 ϵ ‾ t − 2 (5) \sqrt{\alpha_t(1-\alpha_{t-1})} \epsilon_{t-2} + \sqrt{1-\alpha_{t}} \epsilon_{t-1} = \sqrt{1-\alpha_t\alpha_{t-1}} \overline \epsilon_{t-2} \tag{5} αt(1−αt−1)ϵt−2+1−αtϵt−1=1−αtαt−1ϵt−2(5)
其中 ϵ ‾ t − 2 ∼ N ( 0 , I ) \overline \epsilon_{t-2} \sim \mathcal{N}(0, \bold I) ϵt−2∼N(0,I),作为余项的统一表示。代入(4)式,得到:
x t = α t α t − 1 x t − 2 + α t ( 1 − α t − 1 ) ϵ t − 2 + 1 − α t ϵ t − 1 = α t α t − 1 x t − 2 + 1 − α t α t − 1 ϵ ‾ t − 2 (6) \begin{aligned} x_t & = \sqrt{\alpha_t\alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t(1-\alpha_{t-1})} \epsilon_{t-2} + \sqrt{1-\alpha_{t}} \epsilon_{t-1}\\ & = \sqrt{\alpha_t\alpha_{t-1}} x_{t-2} + \sqrt{1-\alpha_t\alpha_{t-1}} \overline \epsilon_{t-2} \end{aligned} \tag{6} xt=αtαt−1xt−2+αt(1−αt−1)ϵt−2+1−αtϵt−1=αtαt−1xt−2+1−αtαt−1ϵt−2(6)
同理继续向下推导,可以得到 x t x_t xt 的通项:
x t = α t x t − 1 + 1 − α t ϵ ‾ t − 1 = α t α t − 1 x t − 2 + 1 − α t α t − 1 ϵ ‾ t − 2 = ⋯ = α t α t − 1 ⋯ α 1 x 0 + 1 − α t α t − 1 ⋯ α 1 ϵ ‾ 0 = α ‾ t x 0 + 1 − α ‾ t ϵ ‾ 0 (7) \begin{aligned} x_t & = \sqrt{\alpha_t} x_{t-1} + \sqrt{1-\alpha_t} \overline \epsilon_{t-1}\\ & = \sqrt{\alpha_t\alpha_{t-1}} x_{t-2} + \sqrt{1-\alpha_t\alpha_{t-1}} \overline \epsilon_{t-2}\\ & = \cdots \\ & = \sqrt{\alpha_t\alpha_{t-1}\cdots\alpha_1} x_{0} + \sqrt{1-\alpha_t\alpha_{t-1}\cdots\alpha_1} \overline \epsilon_{0}\\ & = \sqrt{\overline{\alpha}_t} x_{0} + \sqrt{1-\overline{\alpha}_t} \overline \epsilon_{0}\\ \end{aligned} \tag{7} xt=αtxt−1+1−αtϵt−1=αtαt−1xt−2+1−αtαt−1ϵt−2=⋯=αtαt−1⋯α1x0+1−αtαt−1⋯α1ϵ0=αtx0+1−αtϵ0(7)
由此可以看出,扩散过程通过马尔科夫性质可以一步到位,这也是 diffusion 正向扩散的核心。
三. 逆扩散过程
Diffusion:通过扩散和逆扩散过程生成图像的生成式模型 中已经说了:逆扩散 q ( x t − 1 ∣ x t ) q (x_{t-1} \mid x_t) q(xt−1∣xt) 是未知的,需要用 U-Net 学习 p θ ( x t − 1 ∣ x t ) p_\theta (x_{t-1} \mid x_t) pθ(xt−1∣xt) 来近似;学习过程中使用 q ( x t − 1 ∣ x 0 x t ) q (x_{t-1} \mid x_0x_t) q(xt−1∣x0xt) 来指导 p θ ( x t − 1 ∣ x t ) p_\theta (x_{t-1} \mid x_t) pθ(xt−1∣xt) 进行训练。
1. 背景声明
- q ( x t − 1 ∣ x t ) q (x_{t-1} \mid x_t) q(xt−1∣xt) 是不可知的,但 q ( x t − 1 ∣ x 0 , x t ) q (x_{t-1} \mid x_0, x_t) q(xt−1∣x0,xt) 是可知的,记:
q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ~ ( x t , x 0 ) , β ~ t I ) (8) q\left(x_{t-1} \mid x_t, x_0\right)=\mathcal{N}\left(x_{t-1} ; \tilde{\mu}\left(x_t, x_0\right), \tilde{\beta}_t \mathbf{I}\right) \tag{8} q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)(8) - 使用 q ( x t − 1 ∣ x 0 x t ) q (x_{t-1} \mid x_0x_t) q(xt−1∣x0xt) 来指导 p θ ( x t − 1 ∣ x t ) p_\theta (x_{t-1} \mid x_t) pθ(xt−1∣xt) 进行训练;
- 根据马尔科夫性质,有:
p θ ( x 0 : T ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) (9) p_\theta\left(x_{0: T}\right)=p\left(x_T\right) \prod_{t=1}^T p_\theta\left(x_{t-1} \mid x_t\right) \tag{9} pθ(x0:T)=p(xT)t=1∏Tpθ(xt−1∣xt)(9) - 使用 U-Net 表示 p θ ( x t − 1 ∣ x t ) p_\theta (x_{t-1} \mid x_t) pθ(xt−1∣xt):
p θ ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) (10) p_\theta\left(x_{t-1} \mid x_t\right)=\mathcal{N}\left(x_{t-1} ; \mu_\theta\left(x_t, t\right), \Sigma_\theta\left(x_t, t\right)\right) \tag{10} pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))(10)
2. 公式推导
都说 q ( x t − 1 ∣ x 0 , x t ) q (x_{t-1} \mid x_0, x_t) q(xt−1∣x0,xt) 是可知的,下面推导其表达式。根据贝叶斯公式,有:
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) (11) q\left(x_{t-1} \mid x_t, x_0\right)=q\left(x_t \mid x_{t-1}, x_0\right) \frac{q\left(x_{t-1} \mid x_0\right)}{q\left(x_t \mid x_0\right)} \tag{11} q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt∣x0)q(xt−1∣x0)(11)
其中 q ( x t − 1 ∣ x t , x 0 ) q\left(x_{t-1} \mid x_t, x_0\right) q(xt−1∣xt,x0) 为后验概率, q ( x t ∣ x t − 1 , x 0 ) q\left(x_t \mid x_{t-1}, x_0\right) q(xt∣xt−1,x0) 为似然估计, q ( x t − 1 ∣ x 0 ) q\left(x_{t-1} \mid x_0\right) q(xt−1∣x0) 为先验概率, q ( x t ∣ x 0 ) q\left(x_t \mid x_0\right) q(xt∣x0) 为证据(evidence)。这一步贝叶斯公式巧妙地将逆向过程全部变回了前向。 注意,这里的表示和普通的贝叶斯公式有所不同(多了 x 0 x_0 x0 项)是因为先验概率和证据无法直接求解,需要结合 x 0 x_0 x0 求解得到。
根据扩散过程推出的 x t x_t xt 的通项,即(7)式,有:
q ( x t − 1 ∣ x 0 ) = α ‾ t − 1 x 0 + 1 − α ‾ t − 1 ϵ ∼ N ( α ‾ t − 1 x 0 , 1 − α ‾ t − 1 ) q ( x t ∣ x 0 ) = α ‾ t x 0 + 1 − α ‾ t ϵ ∼ N ( α ‾ t x 0 , 1 − α ‾ t ) (12) \begin{aligned} q\left(x_{t-1} \mid x_0\right)&=\sqrt{\overline{\alpha}_{t-1}} x_0+\sqrt{1-\overline{\alpha}_{t-1}} \epsilon \sim \mathcal{N}\left(\sqrt{\overline{\alpha}_{t-1}} x_0, 1-\overline{\alpha}_{t-1}\right) \\ q\left(x_t \mid x_0\right)&=\sqrt{\overline{\alpha}_t} x_0+\sqrt{1-\overline{\alpha}_t} \epsilon \sim \mathcal{N}\left(\sqrt{\overline{\alpha}_t} x_0, 1-\overline{\alpha}_t\right) \\ \end{aligned} \tag{12} q(xt−1∣x0)q(xt∣x0)=αt−1x0+1−αt−1ϵ∼N(αt−1x0,1−αt−1)=αtx0+1−αtϵ∼N(αtx0,1−αt)(12)
根据(3)式,有:
q ( x t ∣ x t − 1 , x 0 ) = q ( x t ∣ x t − 1 ) = α t x t − 1 + 1 − α t ϵ ∼ N ( α t x t − 1 , 1 − α t ) (13) q\left(x_t \mid x_{t-1}, x_0\right)=q\left(x_t \mid x_{t-1}\right)=\sqrt{\alpha_t} x_{t-1}+\sqrt{1-\alpha_t} \epsilon \sim \mathcal{N}\left(\sqrt{\alpha_t} x_{t-1}, 1-\alpha_t\right) \tag{13} q(xt∣xt−1,x0)=q(xt∣xt−1)=αtxt−1+1−αtϵ∼N(αtxt−1,1−αt)(13)
根据高斯分布定义式,有:
N ( μ , σ 2 ) ∝ exp ( − ( x − μ ) 2 2 σ 2 ) (14) \mathcal{N}\left(\mu, \sigma^2\right) \propto \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right) \tag{14} N(μ,σ2)∝exp(−2σ2(x−μ)2)(14)
将(12)~(14)式代入(11),有:
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) ∝ exp ( − 1 2 ( ( x t − α t x t − 1 ) 2 β t + ( x t − 1 − α ‾ t − 1 x 0 ) 2 1 − a ‾ t − 1 − ( x t − α ‾ t x 0 ) 2 1 − a ‾ t ) ) (15) \begin{aligned} q\left(x_{t-1} \mid x_t, x_0\right)& =q\left(x_t \mid x_{t-1}, x_0\right) \frac{q\left(x_{t-1} \mid x_0\right)}{q\left(x_t \mid x_0\right)} \\ & \propto \exp \left(-\frac{1}{2}\left(\frac{\left(x_t-\sqrt{\alpha_t} x_{t-1}\right)^2}{\beta_t}+\frac{\left(x_{t-1}-\sqrt{\overline{\alpha}_{t-1}} x_0\right)^2}{1-\overline{a}_{t-1}}-\frac{\left(x_t-\sqrt{\overline{\alpha}_t} x_0\right)^2}{1-\overline{a}_t}\right)\right) \\ \end{aligned} \tag{15} q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt∣x0)q(xt−1∣x0)∝exp(−21(βt(xt−αtxt−1)2+1−at−1(xt−1−αt−1x0)2−1−at(xt−αtx0)2))(15)
因为 q ( x t − 1 ∣ x t , x 0 ) q\left(x_{t-1} \mid x_t, x_0\right) q(xt−1∣xt,x0) 是关于 x t − 1 x_{t-1} xt−1 的表达式,因此将(15)式中平方项展开,再按 x t − 1 x_{t-1} xt−1 合并同类项,可得:
exp ( − 1 2 ( ( x t − α t x t − 1 ) 2 β t + ( x t − 1 − α ‾ t − 1 x 0 ) 2 1 − a ‾ t − 1 − ( x t − α ‾ t x 0 ) 2 1 − a ‾ t ) ) = exp ( − 1 2 ( ( α t β t + 1 1 − α ‾ t − 1 ) x t − 1 2 ⏟ x t − 1 方差 − ( 2 α t β t x t + 2 a ‾ t − 1 1 − α ‾ t − 1 x 0 ) x t − 1 ⏟ x t − 1 均值 + C ( x t , x 0 ) ⏟ 与 x t − 1 无关 ) ) (16) \begin{aligned} & \exp \left(-\frac{1}{2}\left(\frac{\left(x_t-\sqrt{\alpha_t} x_{t-1}\right)^2}{\beta_t}+\frac{\left(x_{t-1}-\sqrt{\overline{\alpha}_{t-1}} x_0\right)^2}{1-\overline{a}_{t-1}}-\frac{\left(x_t-\sqrt{\overline{\alpha}_t} x_0\right)^2}{1-\overline{a}_t}\right)\right) \\ = & \exp \left(-\frac{1}{2}\left(\underbrace{\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\overline{\alpha}_{t-1}}\right) x_{t-1}^2}_{x_{t-1} \text { 方差 }} - \underbrace{\left(\frac{2 \sqrt{\alpha_t}}{\beta_t} x_t+\frac{2 \sqrt{\overline{a}_{t-1}}}{1-\overline{\alpha}_{t-1}} x_0 \right) x_{t-1}}_{x_{t-1} \text { 均值 }}+\underbrace{C\left(x_t, x_0\right)}_{\text {与 } x_{t-1} \text { 无关 }}\right)\right) \\ \end{aligned} \tag{16} =exp(−21(βt(xt−αtxt−1)2+1−at−1(xt−1−αt−1x0)2−1−at(xt−αtx0)2))exp −21 xt−1 方差 (βtαt+1−αt−11)xt−12−xt−1 均值 (βt2αtxt+1−αt−12at−1x0)xt−1+与 xt−1 无关 C(xt,x0) (16)
其中 C ( x t , x 0 ) C\left(x_t, x_0\right) C(xt,x0) 是与 x t − 1 x_{t-1} xt−1 无关的表达式,可以提到 exp \exp exp 外作为常数项,因此没有展开。
将(16)式与高斯分布定义式指数展开做对比:
exp ( − ( x − μ ) 2 2 σ 2 ) = exp ( − 1 2 ( 1 σ 2 x 2 − 2 μ σ 2 x + μ 2 σ 2 ) ) \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right)=\exp \left(-\frac{1}{2}\left(\frac{1}{\sigma^2} x^2-\frac{2 \mu}{\sigma^2} x+\frac{\mu^2}{\sigma^2}\right)\right) exp(−2σ2(x−μ)2)=exp(−21(σ21x2−σ22μx+σ2μ2))
提取 x t − 1 x_{t-1} xt−1 的平方项和一次项可得(8)式中方差 β ~ t \tilde{\beta}_t β~t:
∵ 1 β ~ t = 1 σ 2 = ( α t β t + 1 1 − α ‾ t − 1 ) ∴ β ~ t = 1 − α ‾ t − 1 1 − α ‾ t ⋅ β t (17) \because \frac{1}{\tilde{\beta}_t}=\frac{1}{\sigma^2}=\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\overline{\alpha}_{t-1}}\right)\\ \therefore \tilde{\beta}_t=\frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_t} \cdot \beta_t \tag{17} ∵β~t1=σ21=(βtαt+1−αt−11)∴β~t=1−αt1−αt−1⋅βt(17)
同理可得均值 μ ~ t ( x t , x 0 ) \tilde{\mu}_t\left(x_t, x_0\right) μ~t(xt,x0):
∵ 2 μ ~ t ( x t , x 0 ) β ~ t = 2 μ σ 2 = 2 α t β t x t + 2 a ‾ t − 1 1 − α ‾ t − 1 x 0 ∴ μ ~ t ( x t , x 0 ) = α t ( 1 − α ‾ t − 1 ) 1 − α ‾ t x t + α ‾ t − 1 β t 1 − α ‾ t x 0 (18) \because \frac{2 \tilde{\mu}_t\left(x_t, x_0\right)}{\tilde{\beta}_t}=\frac{2 \mu}{\sigma^2}=\frac{2 \sqrt{\alpha_t}}{\beta_t} x_t+\frac{2 \sqrt{\overline{a}_{t-1}}}{1-\overline{\alpha}_{t-1}} x_0 \\ \therefore \tilde{\mu}_t\left(x_t, x_0\right)=\frac{\sqrt{\alpha}_t\left(1-\overline{\alpha}_{t-1}\right)}{1-\overline{\alpha}_t} x_t+\frac{\sqrt{\overline{\alpha}_{t-1}} \beta_t}{1-\overline{\alpha}_t} x_0 \tag{18} ∵β~t2μ~t(xt,x0)=σ22μ=βt2αtxt+1−αt−12at−1x0∴μ~t(xt,x0)=1−αtαt(1−αt−1)xt+1−αtαt−1βtx0(18)
经过上面的分析, x t − 1 x_{t-1} xt−1 可以通过 x 0 x_0 x0 和 x t x_t xt 得到。然而,diffusion 逆向传播时并不知道 x 0 x_0 x0 的情况,因此需要对其进行替换。将(7)式代入,将 x 0 x_0 x0 替换成 x t x_t xt 表示,于是有:
μ ~ t ( x t , x 0 ) = α t ( 1 − α ‾ t − 1 ) 1 − α ‾ t x t + α ‾ t − 1 β t 1 − α ‾ t x 0 = α t ( 1 − α ‾ t − 1 ) 1 − α ‾ t x t + α ‾ t − 1 β t 1 − α ‾ t x t − 1 − α ‾ t ϵ ‾ 0 α ‾ t = 1 a t ( x t − β t 1 − a ‾ t ϵ ‾ 0 ) \begin{aligned} \tilde{\mu}_t\left(x_t, x_0\right)&=\frac{\sqrt{\alpha}_t\left(1-\overline{\alpha}_{t-1}\right)}{1-\overline{\alpha}_t} x_t+\frac{\sqrt{\overline{\alpha}_{t-1}} \beta_t}{1-\overline{\alpha}_t} x_0\\ &=\frac{\sqrt{\alpha}_t\left(1-\overline{\alpha}_{t-1}\right)}{1-\overline{\alpha}_t} x_t+\frac{\sqrt{\overline{\alpha}_{t-1}} \beta_t}{1-\overline{\alpha}_t} \frac{x_t-\sqrt{1-\overline{\alpha}_t} \overline \epsilon_{0}}{\sqrt{\overline{\alpha}_t}}\\ &=\frac{1}{\sqrt{a_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\overline{a}_t}} \overline \epsilon_{0}\right)\\ \end{aligned} μ~t(xt,x0)=1−αtαt(1−αt−1)xt+1−αtαt−1βtx0=1−αtαt(1−αt−1)xt+1−αtαt−1βtαtxt−1−αtϵ0=at1(xt−1−atβtϵ0)
上式中已经消去了 x 0 x_0 x0,只和 t t t 有关,记为 μ ~ t \tilde{\mu}_t μ~t,即:
μ ~ t = 1 a t ( x t − β t 1 − a ‾ t ϵ ‾ 0 ) (19) \tilde{\mu}_t=\frac{1}{\sqrt{a_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\overline{a}_t}} \overline \epsilon_{0}\right) \tag{19} μ~t=at1(xt−1−atβtϵ0)(19)
综上, q ( x t − 1 ∣ x 0 , x t ) q (x_{t-1} \mid x_0, x_t) q(xt−1∣x0,xt) 可以表示为高斯分布采样:
q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; 1 a t ( x t − β t 1 − a ‾ t ϵ ‾ 0 ) , ( 1 − α ‾ t − 1 1 − α ‾ t ⋅ β t ) I ) (20) q\left(x_{t-1} \mid x_t, x_0\right)=\mathcal{N}\left(x_{t-1} ; \frac{1}{\sqrt{a_t}}\left(x_t-\frac{\beta_t}{\sqrt{1-\overline{a}_t}} \overline \epsilon_{0}\right), \left(\frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha}_t} \cdot \beta_t\right) \mathbf{I}\right) \tag{20} q(xt−1∣xt,x0)=N(xt−1;at1(xt−1−atβtϵ0),(1−αt1−αt−1⋅βt)I)(20)
至此, q ( x t − 1 ∣ x 0 , x t ) q (x_{t-1} \mid x_0, x_t) q(xt−1∣x0,xt) 的高斯分布的均值和方差就都有了,只剩下(19)式中的 ϵ ‾ 0 \overline \epsilon_{0} ϵ0,交给 U-Net 使用深度学习方法进行预测。3
需要注意的是,逆扩散过程和扩散过程不同,扩散过程只需要代入(7)式就可以从 x 0 x_0 x0 直接到 x T x_T xT,但逆扩散需要使用(20)式逐步向前递推,从 x T x_T xT 到 x T − 1 x_{T-1} xT−1 一直到 x 0 x_0 x0。

四. 训练过程
前两节分别介绍了 diffusion 正向和逆向扩散过程中的数学公式推导,留下了 ϵ ‾ 0 \overline \epsilon_{0} ϵ0 需要 U-Net 进行预测。因为训练时正向扩散过程中添加的噪声在采样后是已知的,因此只需要训练 U-Net 的预测结果向所添加的噪声靠近即可。记训练过程中的噪声采样为 ϵ \epsilon ϵ,U-Net 的预测噪声为 ϵ θ ( α ‾ t x 0 + 1 − α ‾ t ϵ , t ) \epsilon_{\theta}(\sqrt{\overline{\alpha}_t} x_{0} + \sqrt{1-\overline{\alpha}_t} \epsilon, t) ϵθ(αtx0+1−αtϵ,t),于是有训练过程:

由浅入深了解Diffusion Model ↩︎
一文解释 Diffusion Model (一) DDPM 理论推导 ↩︎
Diffusion扩散模型大白话讲解,看完还不懂?不可能! ↩︎
相关文章:

Diffusion 公式推导
Diffusion:通过扩散和逆扩散过程生成图像的生成式模型 中已经对 diffusion 的原理进行了直观地梳理,本文对其中的数学推导进行讲解,还是基于 DDPM。 目录 一. 预备知识1. 重参数技巧2. 高斯分布的可加性3. 扩散递推式的由来 二. 扩散过程1. 背…...

【C语言快速学习基础篇】之一基础类型、进制转换、数据位宽
文章目录 一、基础类型(根据系统不同占用字节数会有变化)1.1、有符号整形1.2、无符号整形1.3、字符型1.4、浮点型1.5、布尔型 二、进制转换2.1、二进制2.2、八进制2.3、十进制2.4、十六进制2.5、N进制2.6、进制转换关系对应表 三、数据位宽3.1、位3.2、字节3.3、字3.4、双字3.5…...
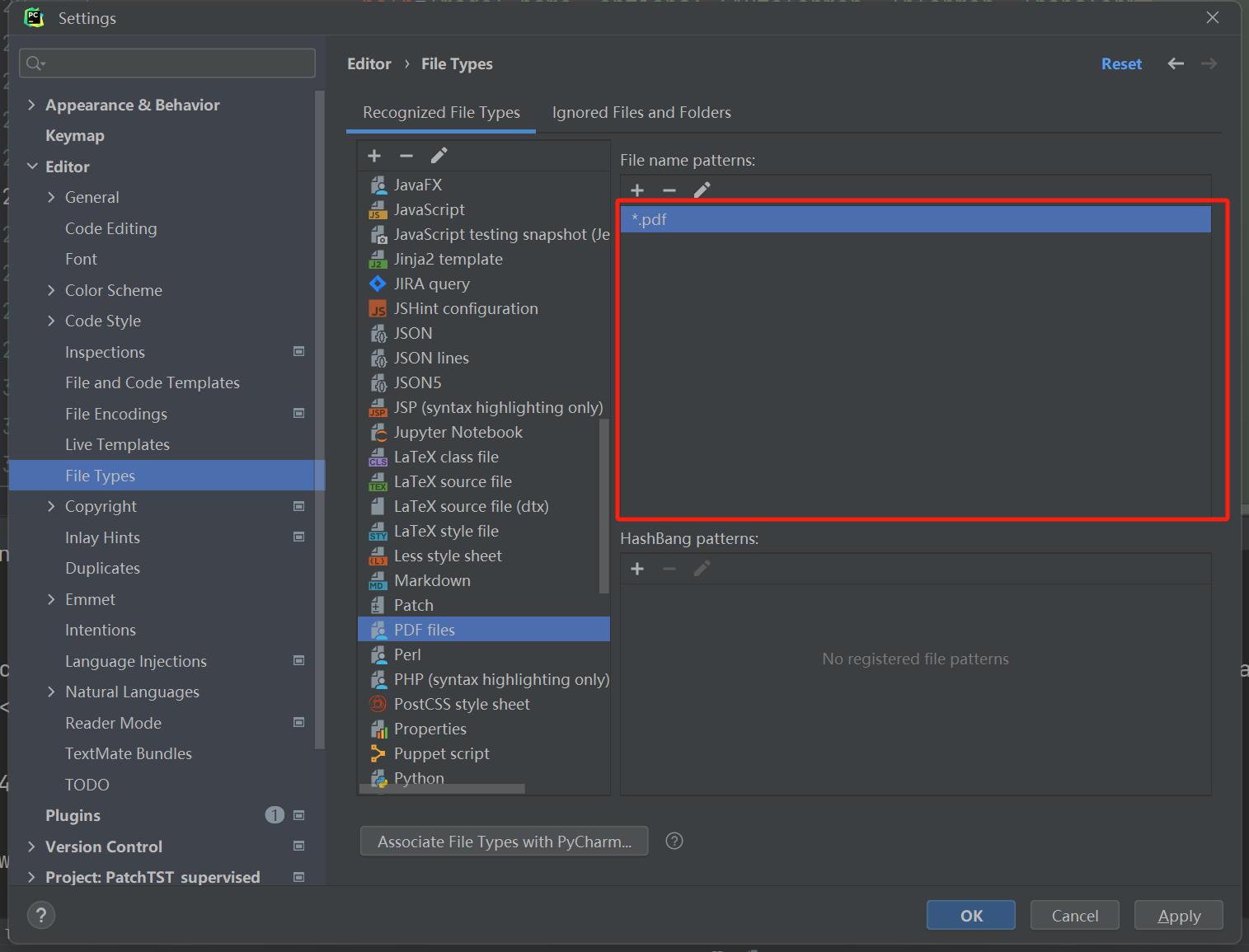
使用GPT-4V解决Pycharm设置问题
pycharm如何实现关联,用中文回答 在PyCharm中关联PDF文件类型,您可以按照以下步骤操作: 1. 打开PyCharm设置:点击菜单栏中的“File”(文件),然后选择“Settings”(设置)。…...

qt 安装
目录 前言 一、QT在线安装包下载 1.官方网站: 2.镜像(清华大学) 二、QT安装 1.更换安装源 2.安装界面 3.组件选择(重点) 参考 Qt2023新版保姆级 安装教程 前言 本文主要介绍2023新版QT安装过程,…...
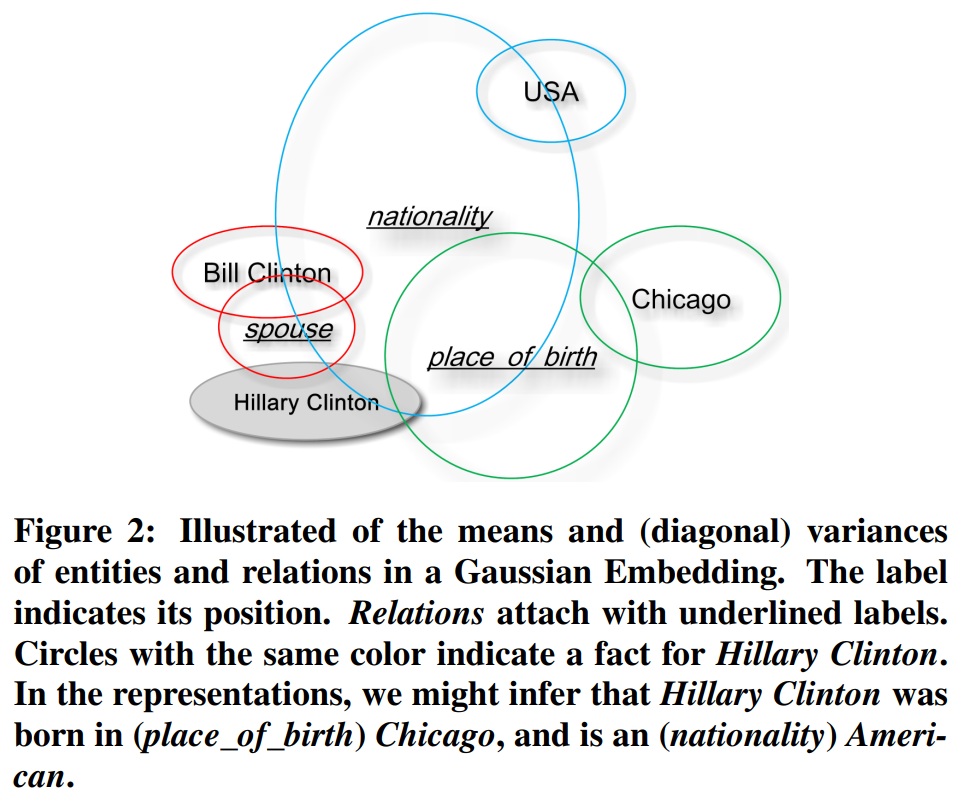
【论文合集】在非欧空间中的图嵌入方法(Graph Embedding in Non-Euclidean Space)
文章目录 1. Hyperbolic Models1.1 Hyperbolic Graph Attention Network1.2 Poincar Embeddings for Learning Hierarchical Representations.1.3 Learning Continuous Hierarchies in the Lorentz Model of Hyperbolic Geometry1.4 Hyperbolic Graph Convolutional Neural Net…...
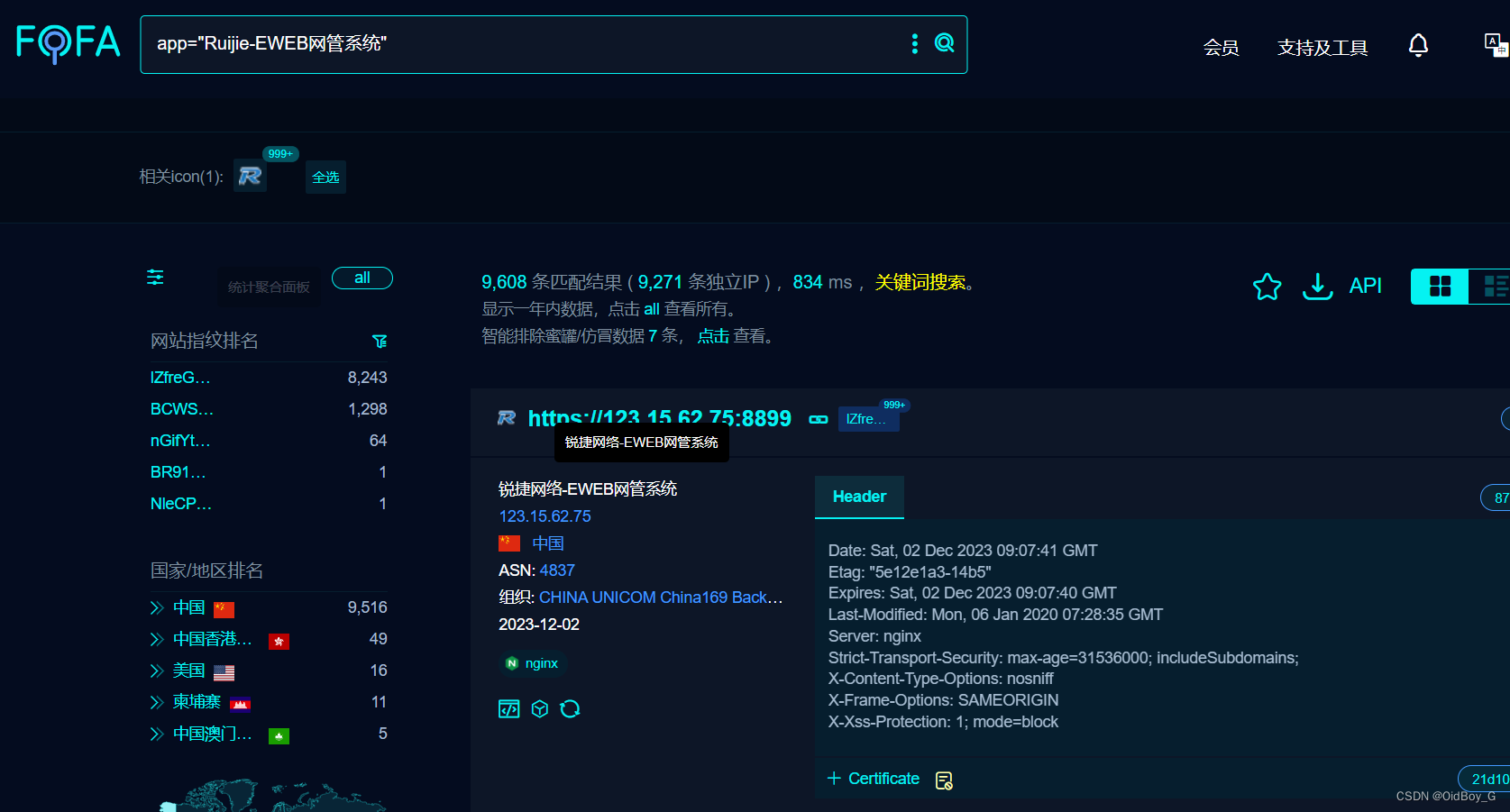
锐捷EWEB网管系统 RCE漏洞复现
0x01 产品简介 锐捷网管系统是由北京锐捷数据时代科技有限公司开发的新一代基于云的网络管理软件,以“数据时代创新网管与信息安全”为口号,定位于终端安全、IT运营及企业服务化管理统一解决方案。 0x02 漏洞概述 Ruijie-EWEB 网管系统 flwo.control.php 中的 type 参数存在…...

Clickhouse在货品标签场景的应用
背景 在电商场景中,我们经常需要对货品进行打标签的操作,简单来说就是对货品进行各种分类,按照价格段进行分组,此时运营人员就可以通过价格段捞取到满足条件的商品了,本文就来简单看下这个场景如何在clickhouse中实现…...

CentOS 7 lvm 更换坏盘操作步骤小记 —— 筑梦之路
背景介绍 硬盘容量不足、硬盘坏道太多等不可控的原因需要更换,要求不能丢失数据进行无损替换硬盘。 操作步骤 1. 将硬盘插入机器,上电连接到服务器 2. 在centos 7 系统中检测是否识别出来硬盘 lsblk 3. 给新插入的硬盘分区 parted /dev/sdc mklabel g…...

zabbix的自动发现和注册、proxy代理和SNMP监控
目录 一、zabbix自动发现与自动注册机制: 1、概念 2、zabbix 自动发现与自动注册的部署 二、zabbix的proxy代理功能: 1、工作流程 2、安装部署 三、zabbix-snmp 监控 1、概念 2、安装部署 四、总结: 一、zabbix自动发现与自动注册…...

以Hub为中心节点的网络技术探析
在计算机网络中,Hub是一个重要的组成部分,它作为中心节点,连接着各个站点,实现数据的传输和通信。本文将对以Hub为中心节点的网络进行深入的技术探析。 首先,我们需要了解什么是Hub。在网络术语中,Hub通常…...

百度推送收录工具-免费的各大搜索引擎推送工具
在互联网时代,网站收录是网站建设的重要一环。百度推送工具作为一种提高网站收录速度的方式备受关注。在这个信息爆炸的时代,对于网站管理员和站长们来说,了解并使用一些百度推送工具是非常重要的。本文将重点分享百度批量域名推送工具和百度…...
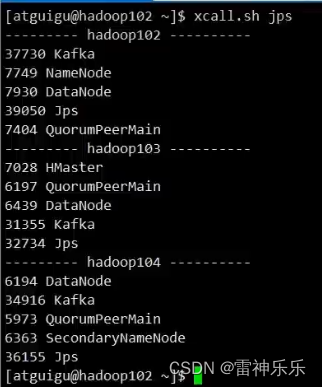
物流实时数仓ODS层——Mysql到Kafka
目录 1.采集流程 2.项目架构 3.resources目录下的log4j.properties文件 4.依赖 5.ODS层——OdsApp 6.环境入口类——CreateEnvUtil 7.kafka工具类——KafkaUtil 8.启动集群项目 这一层要从Mysql读取数据,分为事实数据和维度数据,将不同类型的数据…...

奇迹mu 架设过程中可能会出现的问题及解决办法
通常我们在架设奇迹的时候,可能会遇见这种问题那种问题,很多用户都不知道该如何解决,今天我们就来系统的说明一下一些常见的问题,帮助遇见这些问题的用户理清一个架设的思路,更清楚的判断问题出在哪里,该如…...
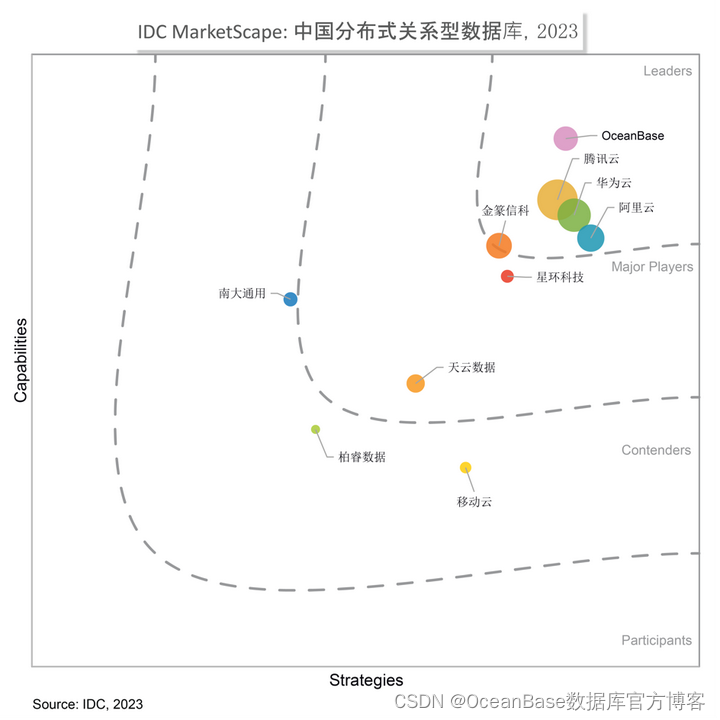
IDC MarketScape2023年分布式数据库报告:OceanBase位列“领导者”类别,产品能力突出
12 月 1 日,全球领先的IT市场研究和咨询公司 IDC 发布《IDC MarketScape:中国分布式关系型数据库2023年厂商评估》(Document number:# CHC50734323)。报告认为,头部厂商的优势正在扩大,OceanBase 位列“领导者”类别。…...

Docker创建mqtt容器mosquitto
#1.创建映射到主机的配置文件/bwss/agent/docker/mosquitto_public/config/mosquitto.conf 内容为: listener 51883 0.0.0.0 # 0.0.0.0 allow_anonymous false persistence false persistence_location /mosquitto/data password_file /mosquitto/config/passwd …...
运维知识点-SQLServer/mssql
SQLServer/mssql Microsoft structed query language常见注入提权 技术点:0x00 打点前提 0x01 上线CS0x02 提权0x03 转场msf0x04 抓取Hash0x05 清理痕迹 Microsoft structed query language 常见注入 基于联合查询注入 order by 判断列数(对应数据类型…...

Reactor实战,创建一个简单的单线程Reactor(理解了就相当于理解了多线程的Reactor)
单线程Reactor package org.example.utils.echo.single;import java.io.IOException; import java.net.InetSocketAddress; import java.nio.channels.*; import java.util.Iterator; import java.util.Set;public class EchoServerReactor implements Runnable{Selector sele…...
)
NoSQL大数据存储技术测试题(参考答案)
目录 1.绪论 2.NoSQL数据库的基本原理 4.HBase的基本原理与使用 5.HBase高级原理 7.MongoDB 8.其他NoSQL数据库 1.绪论 总分: 14.0 10分 单项选择题 4分 判断题 教师评语: 一 单项选择题(10分) 1、NoSQL一词表示的含义是()。…...

Python查看文件列表
os.listdir 是 Python 的一个内置函数,用于列出指定目录中的所有文件和子目录。它接受一个字符串参数,即要列出内容的目录的路径。 列出当前工作目录中的所有文件和子目录 files_and_dirs os.listdir() print(files_and_dirs) 列出指定目录中的所…...
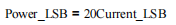
INA219电流感应芯片_程序代码
详细跳转借鉴链接INA219例程此处进行总结 简单介绍一下 INA219: 1、 输入脚电压可以从 0V~26V,INA219 采用 3.3V/5V 供电. 2、 能够检测电流,电压和功率,INA219 内置基准器和乘法器使之能够直接以 A 为单位 读出电流值。 3、 16 位可编程地…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
