【数据结构】关于二叉树你所应该知道的数学秘密
目录
1.什么是二叉树(可以跳过 目录跳转)
2.特殊的二叉树(满二叉树/完全二叉树)
2.1 基础知识
2.2 满二叉树
2.3 完全二叉树
3.二叉树的数学奥秘(主体)
3.1 高度与节点个数
3.2* 度
4.运用二叉树的数学奥秘做题
4.1 P1
4.2 P2
4.3 P3
4.4 P4
1.什么是二叉树(可以跳过 目录跳转)
数据结构当中,树是一种很重要的结构,在树当中,二叉树又是极为特殊、应用广泛的一种,那什么是二叉树呢?
我们首先回忆一下“度”的概念,树是由节点组织起来的,每一个节点都有自己的分叉,即自己的子树个数。如图中的 1节点,它的度就是3,因为 1节点是有三个分叉 / 子树 2 3 4。再如图中的 4节点,它的度就是1,因为 1节点是有三个分叉 / 子树 8。再比如图中的 9节点,它的度就是0,因为它压根就没有分叉 / 子树。

而二叉树,就是在树的基础上,规定:
1. 二叉树的所有节点的度都是小于等于2的,二叉树不存在度大于2的节点。通俗一点理解,二叉树的节点最多有两个叉 / 子树,也可能只有一个叉,甚至没有叉。
2. 二叉树有左右子树之分,一个节点最多有两个分叉,一个节点的左边的子树叫做左子树,右边的子树叫做右子树。举个下图中的例子,3节点的左子树就是2子树,3节点的右子树就是8子树;8的左子树是6子树,8节点的右子树是空NULL(空树);4节点的左右子树都是空树NULL。还有这个节点的子树的左右顺序是固定的,次序不能颠倒,也因此二叉树是有序树。
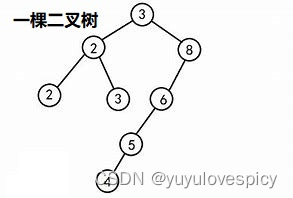
轻松一下,例如现实当中下面这棵树就是一棵二叉树(当然你需要把这棵树倒转一下看):(度都小于等于2)

2.特殊的二叉树(满二叉树/完全二叉树)
2.1 基础知识
首先对一个普通二叉树,我们要建立层与高度的概念,如图,根节点3是第一层,第一层有2个节点;节点2和节点8组成了第二层,第二层有2个节点;节点2 3 6处在二叉树的第三层,二叉树的第三层有3个节点。这棵二叉树的高度h==5。

2.2 满二叉树
在这个基础之上,我们引入满二叉树的概念,如果一个二叉树高h,那么满二叉树就是每一层的节点的个数都达到了MAX最大值,也就是对于第k层来说,它一定有2 ^(k-1)个节点。所以根据等比数列来说,这个满二叉树它的总结点个数一定是2^0 + 2^1 +2^2 + 2^3 +...... + 2^(h-1) == 2^h - 1个节点。反过来讲,如果一棵满二叉树的总节点个数为N,那它的高度就是log2(N+1)。
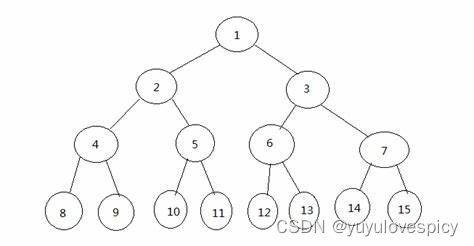
如上面的三个图,第一个图和第二个图,他们都是满二叉树,因为他们的每一层节点的个数都已经达到了最大值(第k层都是2^(k-1)个节点)。但是第三个图,这个二叉树的最后一层,也就是第4层,个数没有达到这一层所能达到的最大值,所以第三个图就不是满二叉树。
不过,第三个图,它虽然不是满二叉树,但是他是完全二叉树!
2.3 完全二叉树
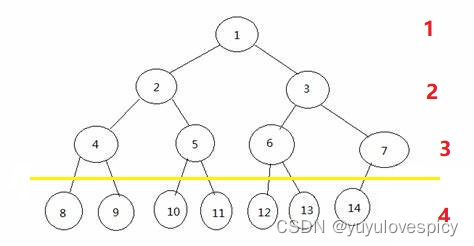
先不去看复杂的概念,我们假设一棵完全二叉树有h层,就拿图中这个完全二叉树,它有的高度h是4。
那么如果只看最后一层往上的h-1个层(本例中就是上3层),暂时不看最后一层(不看第4层),如果一棵整树是完全二叉树,那么上h-1层就是一棵满二叉树(你看第1 2 3层组成的二叉树就是一棵满二叉树),这是第一点完全二叉树所满足的。
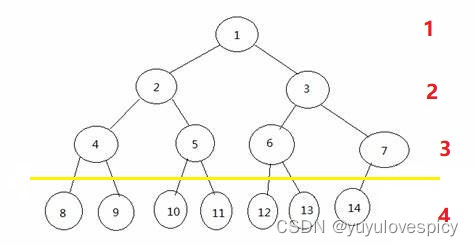
然后第二点,我们只看最后一层,如果一棵整树是完全二叉树,那么这最后一层(也就是图上的第4层)的所有节点,在顺序上,是连续的,没有跳跃间隔的!!!关于连续的没有跳跃间隔的,我们看一下例子就明白了:
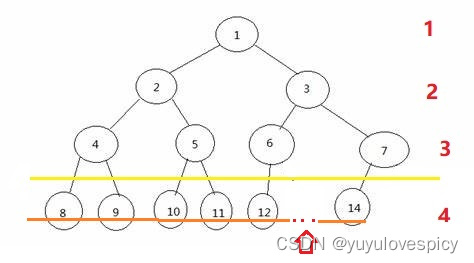
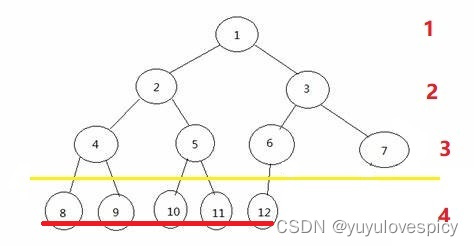
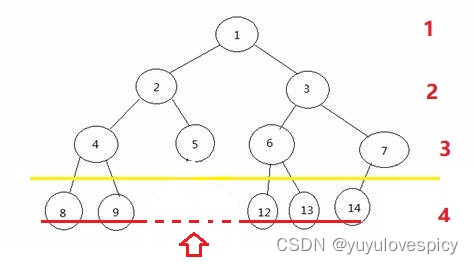
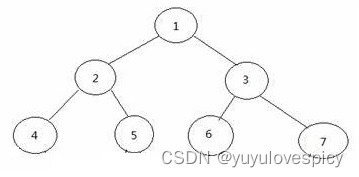
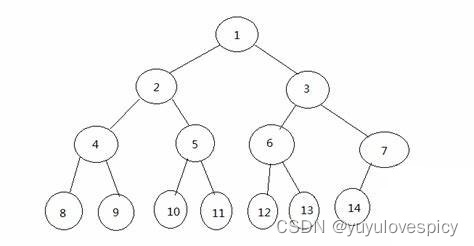
看第一个图,我们看最后一层的所有节点,它就不是完全连续的,是有间断的,所以这棵树不是完全二叉树;第二个图的的最后一层的所有节点,它是完全连续的,所以这棵树是完全二叉树;第三个图的最后一层的所有节点,它就不是完全连续的,是有间断的,所以这棵树不是完全二叉树。
所以只要满足以下两点,这就是一棵完全二叉树(设其高度为h):
1.上h-1层构成一棵满二叉树。
2.第h层所有节点,在顺序上,是连续的,没有跳跃间隔的。
所以其实,一棵满二叉树,一定是一棵完全二叉树,因为满二叉树上h-1层是满二叉树,且其最后一层也是连续的,没有跳跃间隔的。
3.二叉树的数学奥秘(主体)
3.1 高度与节点个数
在假设根节点是第1层,不讨论空树的情况下:
秘密1:如果树有h层。对于某一层来说,比如对于第k层,这一层所有节点的个数最多是2^(k-1)个。
秘密2:如果树有h层,那这棵树总结点的最大个数,就是2^h - 1个。

秘密3:如果一棵满二叉树的高度为h,那它的所有节点个数和是2^h - 1。
如果一棵满二叉树的总节点个数和为N,那它的高度就是log2(N+1)。
秘密4:如果一棵完全二叉树的高度为h,那它的所有节点个数和是在这样一个区间 :( 2^(h-1),2^h - 1 ],左开右闭。
如果一棵完全二叉树的节点个数和为N,那么它的高度就是log2(N+1),必须注意 log2(N+1)可能不是整数,如果不是整数那就默认往大取整。其实很好区分,如果N+1恰好是2的指数的结果,那么高度就是log2(N+1),而如果N+1不是2的指数的结果,那么高度就是把N+1往大补成2的指数的结果,高度是往大取整的log2(N+1)。

详情练习,请跳转至4.1。
3.2* 度
度,每一个节点都有自己的度,度就是一个节点的分叉数,即往下有多少棵子树。
对于任何一棵二叉树,度为0的节点的数量,也即叶子节点的数量为n0,度为2的分支节点的数量为n2。那么一定满足n0 = n2 + 1。也即度为0的节点的数量,永远比度为2的节点的数量多1个!!!
我们随便举几个例子,你可以发现度,都满足上述关系!

如果二叉树只有一个根节点,它的度是0,度为2的节点不存在,n0 = 1,n2 = 0,n0 = n2 + 1。
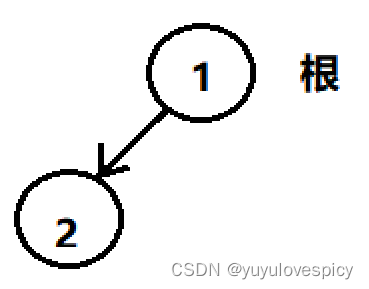
如上图二叉树,节点1的度为1,节点2的度为0,n0 = 1,n2 = 0,n0 = n2 + 1。
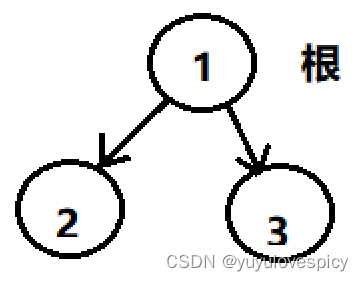
如上图二叉树,节点1的度为2,节点2的度为0,节点3的度为0,n0 = 2,n2 = 1,n0 = n2 + 1。
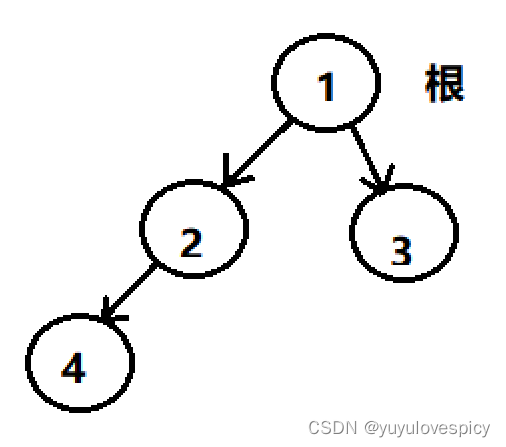
如上图二叉树,节点1的度为2,节点2的度为1,节点3的度为0,节点4的度是0,n0 = 2,n2 = 1,n0 = n2 + 1。
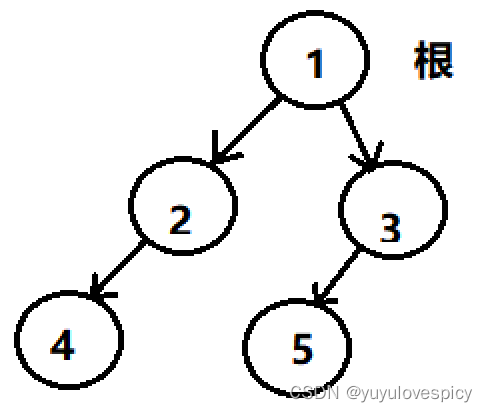
如上图二叉树,节点1的度为2,节点2的度为1,节点3的度为1,节点4的度是0,节点5的度为0,n0 = 2,n2 = 1,n0 = n2 + 1。
由此迭代判断,其实所有的二叉树都是满足n0 = n2 + 1这个数学奥秘的。度为0的节点永远比度为2的节点的数量多一个!
简单的从数学的角度证明一下这个结论:
一棵二叉树的总度数n=度数为0的节点的数量n0×0+度数为1的节点的数量n1×1+度数为2的节点的数量n2×2。
一棵二叉树的总度数n同时=所有节点个数n0+n1+n2-1。
由上述两个式子可得n1+2n2=n0+n1+n2-1。
所以有n0=n2+1。
4.运用二叉树的数学奥秘做题
4.1 P1
1.某二叉树共有399个结点。其中有199个度为2的结点。 则读二又树中的叶子结点数为()
A. 不存在这样的二叉树
B. 200
C. 198
D. 199
提取题目信息:n0 + n1 + n2=399;n2 = 199;而且结合我们知道的数学秘密,n0 = n2 + 1;所以n0 = 200。所以题干给的第一句话是废的!我们只要通过第二句话,结合n0 = n2 + 1,就可以知道,叶子节点的个数,即度为0的节点的个数为200。故选B。
4.2 P2
2.在具有2n个结点的完全二叉树中,叶子结点个数为()
A. n
B. n+1
C. n-1
D. n/2
提取题目信息:n0 + n1 + n2 = 2n,和是一个偶数。然后这是一棵完全二叉树,完全二叉树有一个十分重要的特点,注意观察下图,度为1的节点个数只能有1个或0个!然后再无其他个数(最后一层的节点的度都是0,上面是一个满二叉树,出现度为1的节点数目只能最多有1个),所以完全二叉树中,度为1的节点个数 n1 非0即1,非1即0。
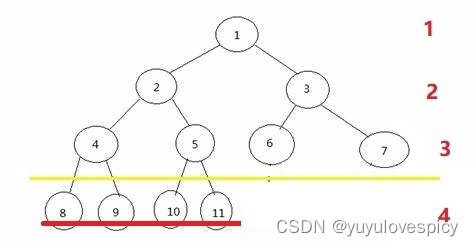
n0 = n2 + 1,这个奥秘,我们结合题设n0 + n1 + n2 = 2n,则2*n2 + 1 + n1 = 2n。等式左侧的2*n2 + 1,是一个奇数,然后这个奇数加上了n1;等式的右侧2n,是一个偶数。奇数只能通过加一个奇数,才能得到偶数!所以n1是奇数。
n1非0即1,n1是奇数,所以n1 == 1。
所以2*n2 +1 + 1 = 2n;所以度为2的节点的个数n2 = n-1。所以叶子节点的个数n0 = n2 + 1 = n - 1 + 1 = n;故选A。
4.3 P3
3.一棵完全二叉树的节点数为531个,那么这棵树的高度为()
A 11
B 10
C 8
D 12
我们直接根据3.1当中的规律,N=531,我们把N+1 == 532,log2(532),往大取整就是层数,2^9 == 512 < 532 < 2^10 == 1024,往上取整,则一共有10层。故选B。
4.4 P4
4.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
n0 + n1 + n2 = 767,完全二叉树n1不是1就是0,n0 + n2 = n0 + n0 - 1 = 2*n0 - 1,是一个奇数。2*n0 - 1 + n1 = 767,右侧是奇数,所以左侧的奇数2*n0 - 1,必须通过加一个偶数,才能保持其是奇数,所以n1是偶数,又n1 非1即0,所以n1 == 0。所以2*n0 - 1 = 767,所以叶子节点的个数n0 = 768/2 = 384。故选B。
相关文章:

【数据结构】关于二叉树你所应该知道的数学秘密
目录 1.什么是二叉树(可以跳过 目录跳转) 2.特殊的二叉树(满二叉树/完全二叉树) 2.1 基础知识 2.2 满二叉树 2.3 完全二叉树 3.二叉树的数学奥秘(主体) 3.1 高度与节点个数 3.2* 度 4.运用二叉树的…...

哈希表题目:猜数字游戏
文章目录题目标题和出处难度题目描述要求示例数据范围解法一思路和算法代码复杂度分析解法二思路和算法代码复杂度分析题目 标题和出处 标题:猜数字游戏 出处:299. 猜数字游戏 难度 4 级 题目描述 要求 你在和朋友一起玩猜数字(Bulls…...
项目请求地址自动加上了本地ip的解决方式
一般情况下来说都是一些粗心大意的问题导致的 场景一:少加了/ 场景二:前后多加了空格 场景三:拼接地址错误
Vue3 企业级项目实战:项目须知与课程约定
本节内容很重要,希望大家能够耐心看完。 Vue3 企业级项目实战 - 程序员十三 - 掘金小册Vue3 Element Plus Spring Boot 企业级项目开发,升职加薪,快人一步。。「Vue3 企业级项目实战」由程序员十三撰写,2744人购买https://s.ju…...

传导EMI抑制-Π型滤波器设计
1 传导电磁干扰简介 在开关电源中,开关管周期性的通断会产生周期性的电流突变(di/dt)和电压突变(dv/dt),周期性的电流变化和电压变化则会导致电磁干扰的产生。 图1所示为Buck电路的电流变化,在Buck电路中上管电流和下…...

如何在excel中创建斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:…...
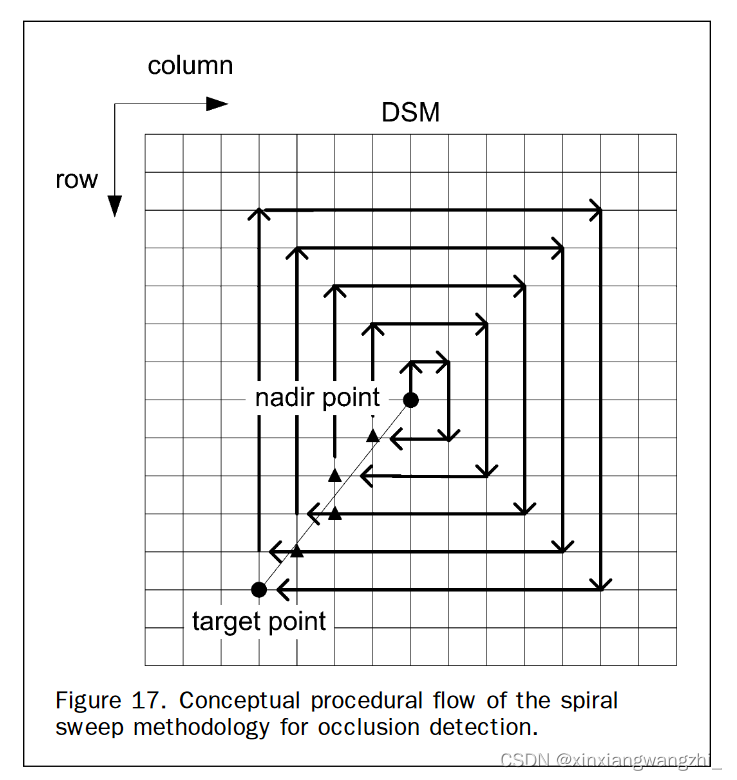
遮挡检测--基于角度的遮挡检测方法
文章目录1基于角度的遮挡检测方法2遮挡检测遍历方法2.1方法1--自适应径向扫描方法2.2方法2--螺旋扫描法参考1基于角度的遮挡检测方法 在基于角度的方法中,通过依次分析DSM中沿径向方向的投影光线的角度来识别遮挡。定义α\alphaα角:DSM三维点与相机中心…...
)
【luogu CF1098D】Eels(结论)
Eels 题目链接:luogu CF1098D 题目大意 有一个可重集,每次操作会放进去一个数或者取出一个数。 然后每次操作完之后,问你对这个集合进行操作,每次选出两个数 a,b 加起来合并回去,直到集合中只剩一个数,要…...
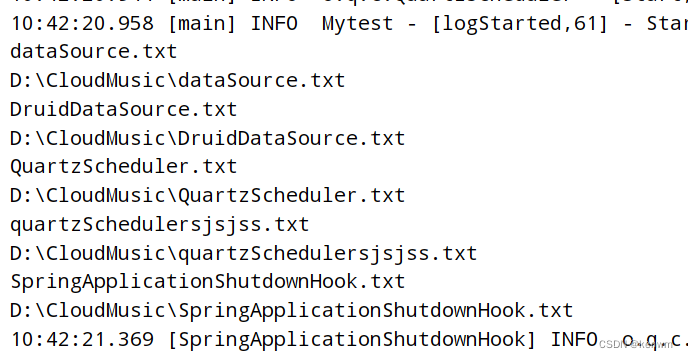
【java】遍历文件夹输出所有文件的文件名与绝对路径,在windows环境
【java】遍历文件夹输出所有文件的文件名与绝对路径,在windows环境 String filepath "D:\\CloudMusic\\";//D盘下的file文件夹的目录File file new File(filepath);//File类型可以是文件也可以是文件夹File[] fileList file.listFiles();//将该目录下的…...
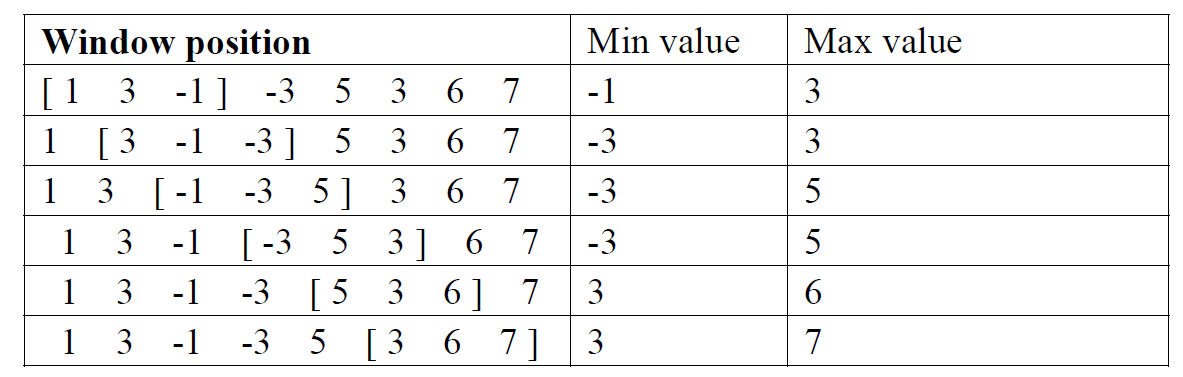
Window问题详解(下)
建议先看一下 Window问题详解(上) 思路② 既然会超时,那该怎么办呢? 显然需要一个更快速的方法来解决这个问题! 我们先来观察一下图片: 我们发现,每一次选中的数都会增加下一个。 !!!!! 因此,我们可以根据此特性优化时间!! 第一次先求出前 k − 1 k-1 k−...

Kafka部署与SpringBoot集成
Kafka与ZooKeeper Apache ZooKeeper是一个基于观察者模式的分布式服务管理框架,即服务注册中心。同时ZooKeeper还具有存储数据的能力。Kafka的每台服务器作为一个broker注册到ZooKeeper,多个broker借助ZooKeeper形成了Kafka集群。同时ZooKeeper会保存一…...
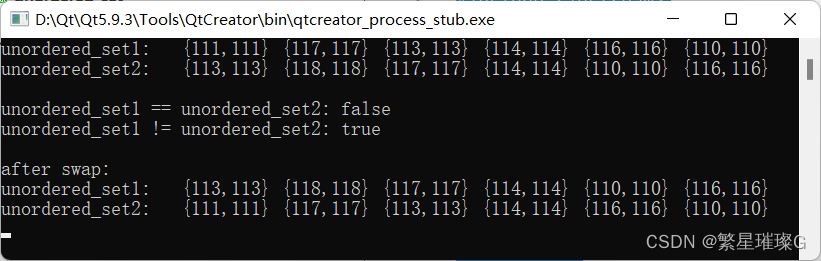
c++11 标准模板(STL)(std::unordered_set)(十三)
定义于头文件 <unordered_set> template< class Key, class Hash std::hash<Key>, class KeyEqual std::equal_to<Key>, class Allocator std::allocator<Key> > class unordered_set;(1)(C11 起)namespace pmr { templ…...

【2023】DevOps、SRE、运维开发面试宝典之ELKStack相关面试题
文章目录 1、elasticsearch的应用场景2、elasticsearch的特点3、Elasticsearch集群三种状态分别是什么?代表什么?4、Elasticsearch集群的优化方面5、Elasticsearch集群防止脑裂的配置参数?6、ELK日志采集平台架构组件介绍?7、Logstash组件的作用?8、收集Kubernetes集群程序…...

Hive中的高阶函数(二)
1、UDTF之explode函数 explode(array)将array列表里的每个元素生成一行; explode(map)将map里的每一对元素作为一行,其中key为一列,value为一列; 一般情况下,explode函数可以直接使用即可,也可以根据需要结…...

Java集合知识点总结
ArrayListLinkedListLinkedHashSetHashSetTreeSetHashTableHashMapTreeMap是否有序有序有序有序无序自然排序(Comparator)进行排序,默认升序使用的是重写comparTo方法无序无序自动排序元素是否为空可为null可为null不允许可为null不允许键允许…...
培训班出身的同学简历怎么做?面试要注意哪些?来自资深大厂HR的忠告
目录 1 不少培训班候选人的简历中,缺乏足够的商业项目年限 2 直接描述培训班学习经历会带来的负面影响 3 大龄转行Vs年轻的初级程序员,公司一般会如何选择? 4 经过培训班突击后,可以先面试小公司 5 面试官怎么面试有培训班经历…...
Hive3.1.3安装部署_最小化部署_元数据MySQL部署_Hiveserver2部署_metastore部署---大数据之Hive工作笔记0012
hbase 实时分析 hive 离线分析 这里是新版本的hive3.1.3的安装 关于hive的原理之前的博客已经详细说了 可以看到上面是hive运行的原理图 词法分析 语法分析...
 含义)
javascript:void(0) 含义
我们经常会使用到 javascript:void(0) 这样的代码,那么在 JavaScript 中 javascript:void(0) 代表的是什么意思呢?javascript:void(0) 中最关键的是 void 关键字, void 是 JavaScript 中非常重要的关键字,该操作符指定要计算一个表…...

不用机器学习不用大数据,给你讲通ChatGPT的深层原理
ChatGPT现在看来已经异常火爆了,很多人已经熟知,并且开始练习使用或者开始利用他开始实践了。但仍然有很多人在观望,在疑惑,今天狗哥不用那些高端大气的机器学习亦或是大数据还给你讲通ChatGPT深层到底是个啥逻辑。 目录 1. 聊家…...

JavaScript中的循环类型
JavaScript 中有三种主要的循环类型: for、while 和 do...while。 for: 循环指定次数。 例如: for (let i 0; i < 5; i) {console.log(i); } while: 当条件为真时循环。 例如: let i 0; while (i < 5) {console.log(i);i; } do...while: 先执…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...
