探究Logistic回归:用数学解释分类问题
文章目录
- 前言
- 回归和分类
- Logistic回归
- 线性回归
- Sigmoid函数
- 把回归变成分类
- Logistic回归算法的数学推导
- Sigmoid函数与其他激活函数的比较
- Logistic回归实例
- 1. 数据预处理
- 2. 模型定义
- 3. 训练模型
- 4. 结果可视化
- 结语
前言
当谈论当论及机器学习中的回归和分类问题时,很容易被“Logistic回归”中的“回归”一词所误导。尽管Logistic回归中有"回归"二字,但它实际上是一种用于分类问题的算法,而不是回归问题。在这篇博客中,我们将深入研究Logistic回归,讨论其背后的原理以及如何手动实现它。
回归和分类
在机器学习领域,回归(Regression) 和 分类(Classification) 是两种主要的预测问题类型。回归和分类都属于监督学习,但它们解决的问题不同。
- 回归问题: 旨在预测一个连续值,例如房屋价格、股票价格、销售额等。
- 分类问题: 关注对数据进行离散类别的预测,将数据分为不同的类别,比如预测一封电子邮件是否为垃圾邮件等。
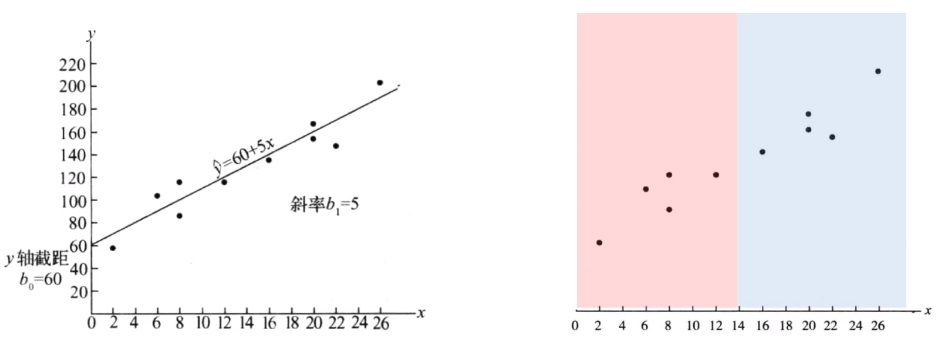
不要被Logistic回归的名字所欺骗,Logistic回归虽然带有 “回归” 二字,但实质上是一种用于二分类的算法。
Logistic回归
Logistic回归是一种基于概率的线性分类算法,尤其适用于解决二分类问题。
与线性回归不同,它通过将线性函数的输出映射到一个介于0和1之间的概率来实现分类。就这样把连续的预测值转换为概率输出的形式,这个概率可以表示为样本属于某个类别的概率。
在Logistic回归中,我们使用一个称为Sigmoid函数的特殊函数,他叫Logistic(逻辑)函数,也叫激活函数。
简单来说:Logistic回归 = 线性回归 + Sigmoid函数
线性回归
首先,让我们回顾一下线性回归。
线性回归是一种用于建模自变量(输入特征)与因变量(输出)之间线性关系的模型。
线性回归的目标是找到一条直线(或超平面),最大程度地拟合输入数据。其数学表达式为:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β n X n + ϵ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_nX_n + \epsilon Y=β0+β1X1+β2X2+…+βnXn+ϵ
其中, Y Y Y 是预测值, β 0 \beta_0 β0 是截距, β 1 , β 2 , … , β n \beta_1, \beta_2, \ldots, \beta_n β1,β2,…,βn 是权重, X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn 是特征, ϵ \epsilon ϵ 是误差。
线性模型可以表示为:
h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n h(x)=θ0+θ1x1+θ2x2+...+θnxn
其中, h ( x ) h(x) h(x) 是预测值, θ 0 , θ 1 , . . . , θ n \theta_0, \theta_1, ..., \theta_n θ0,θ1,...,θn 是模型的参数。
Sigmoid函数
为了将线性回归转变为分类问题,我们引入了Sigmoid函数。
Sigmoid函数是一种常用的激活函数,其图像呈S形状。它的特点是在输入接近正无穷或负无穷时,输出趋近于1或0,而在接近零时,输出约为0.5。
这种性质使得sigmoid函数在将线性输出映射到概率时非常有用。它的导数也相对简单,这对于梯度下降等优化算法至关重要。
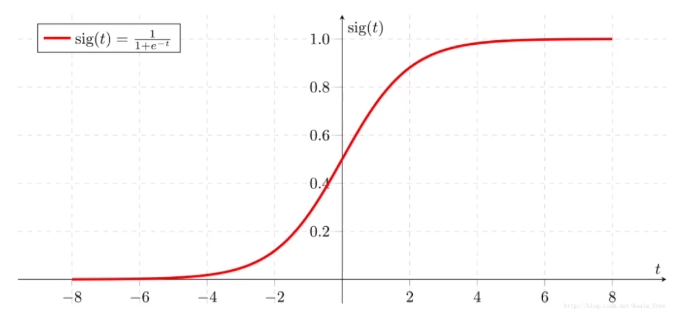
把回归变成分类
Sigmoid函数将任意实数值映射到一个范围在0和1之间的概率值。其表达式为:
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
这里, z z z 是线性模型的输出。将Sigmoid函数应用于线性模型的输出,我们得到了Logistic回归的基本公式:
h ( x ) = σ ( θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n ) h(x) = \sigma(\theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n) h(x)=σ(θ0+θ1x1+θ2x2+...+θnxn)
通过这个转换,我们可以将任意实数范围内的输出映射到 [ 0 , 1 ] [0, 1] [0,1]之间。
Logistic回归算法的数学推导
现在我们已经得知Logistic回归是一种分类算法,它使用一个Sigmoid函数将输入映射到0和1之间的概率值。
假设我们有一个样本 x x x,那么它属于类别1的概率可以表示为:
P ( y = 1 ∣ x ) = 1 1 + e − ( w T x + b ) P(y=1|x) = \frac{1}{1+e^{-(w^Tx + b)}} P(y=1∣x)=1+e−(wTx+b)1
其中, w w w 是特征的权重向量, x x x 是输入特征向量, b b b是偏置项(bias)。我们可以将所有样本的预测结果表示为一个向量:
y ^ = σ ( X w + b ) \hat{y} = \sigma(Xw+b) y^=σ(Xw+b)
其中, σ ( x ) \sigma(x) σ(x)是Sigmoid函数:
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+e^{-x}} σ(x)=1+e−x1
我们的目标是最小化交叉熵损失函数:
J ( w , b ) = − 1 m ∑ i = 1 m [ y ( i ) log ( y ^ ( i ) ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ] J(w,b) = -\frac{1}{m}\sum_{i=1}^{m}{[y^{(i)}\log(\hat{y}^{(i)})+(1-y^{(i)})\log(1-\hat{y}^{(i)})]} J(w,b)=−m1i=1∑m[y(i)log(y^(i))+(1−y(i))log(1−y^(i))]
其中, m m m是样本数量, y ( i ) y^{(i)} y(i)是第 i i i个样本的真实标签, y ^ ( i ) \hat{y}^{(i)} y^(i)是它的预测结果。我们可以使用梯度下降法来最小化损失函数。权重和偏置项的更新规则如下:
w = w − α ∂ J ( w , b ) ∂ w w = w - \alpha\frac{\partial J(w,b)}{\partial w} w=w−α∂w∂J(w,b)
b = b − α ∂ J ( w , b ) ∂ b b = b - \alpha\frac{\partial J(w,b)}{\partial b} b=b−α∂b∂J(w,b)
其中, α \alpha α是学习率。我们可以通过计算损失函数对权重和偏置项的偏导数来得到它们的梯度:
∂ J ( w , b ) ∂ w = 1 m X T ( y ^ − y ) \frac{\partial J(w,b)}{\partial w} = \frac{1}{m}X^T(\hat{y}-y) ∂w∂J(w,b)=m1XT(y^−y)
∂ J ( w , b ) ∂ b = 1 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) \frac{\partial J(w,b)}{\partial b} = \frac{1}{m}\sum_{i=1}^{m}{(\hat{y}^{(i)}-y^{(i)})} ∂b∂J(w,b)=m1i=1∑m(y^(i)−y(i))
Sigmoid函数与其他激活函数的比较
Sigmoid函数在Logistic回归中被广泛使用,因为它能将输出转化为概率值。
除了sigmoid函数,还有其他一些常用的激活函数,比如ReLU(Rectified Linear Unit)函数。这些函数在神经网络和深度学习中扮演着重要的角色。
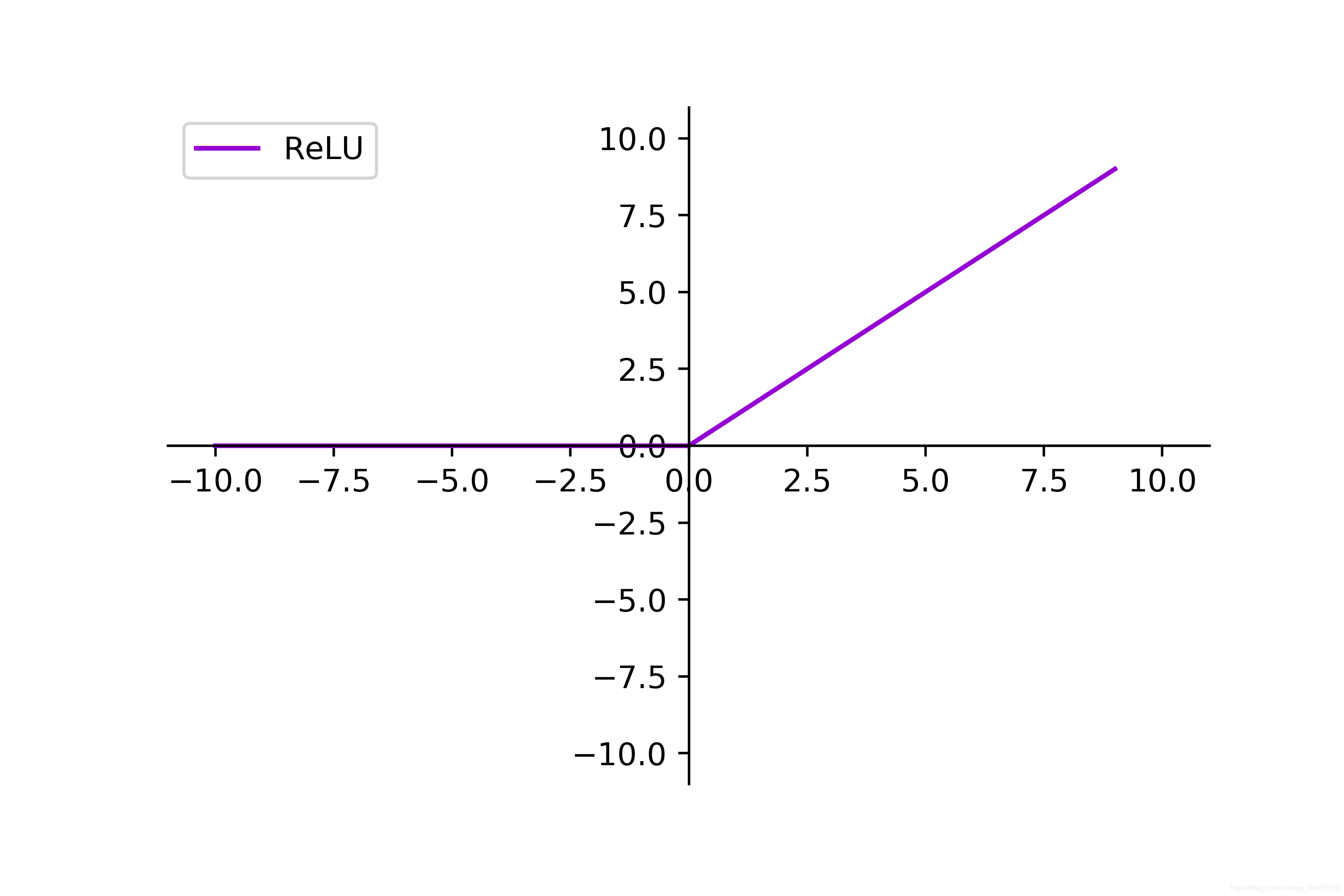
相比于Sigmoid函数,ReLU的主要优势在于它的计算速度更快且更容易收敛,并且在处理大规模数据和深层神经网络时表现更好。它解决了梯度消失问题,并且能够更好地适应非线性关系。
每种激活函数都有自己的特点和适用范围,在实际应用中,选择使用哪种激活函数取决于具体的问题和数据集特征。如果需要将输出转化为概率值,Logistic回归中的Sigmoid函数是一个不错的选择。如果需要处理更复杂的非线性关系,深度学习中的ReLU函数可能更适合。
Logistic回归实例
1. 数据预处理
首先,我们需要加载数据集,数据使用Scikit-learn里的鸢尾花数据集(Iris Dataset)。在Scikit-learn中,可以使用load_iris()函数来加载数据集。为了简化问题,我们只使用两个特征:萼片长度(sepal length)和花瓣长度(petal length)。同时,我们只考虑两个类别:山鸢尾(Iris-setosa)和变色鸢尾(Iris-versicolor),并将它们分别标记为0和1。
from sklearn.datasets import load_iris
import numpy as npiris = load_iris()
X = iris.data[:, [0, 2]]
y = (iris.target != 0) * 1print('Number of examples:', len(y))
print('Number of features:', X.shape[1])
print('Classes:', np.unique(y))
输出:
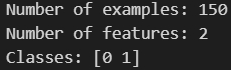
2. 模型定义
接下来,我们定义Logistic回归模型。
def sigmoid(x):return 1 / (1 + np.exp(-x))class LogisticRegression:def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):self.lr = lrself.num_iter = num_iterself.fit_intercept = fit_interceptself.verbose = verbosedef __add_intercept(self, X):intercept = np.ones((X.shape[0], 1))return np.concatenate((intercept, X), axis=1)def __loss(self, h, y):return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()def fit(self, X, y):if self.fit_intercept:X = self.__add_intercept(X)self.theta = np.zeros(X.shape[1])for i in range(self.num_iter):z = np.dot(X, self.theta)h = sigmoid(z)gradient = np.dot(X.T, (h - y)) / y.sizeself.theta -= self.lr * gradientif self.verbose and i % 10000 == 0:z = np.dot(X, self.theta)h = sigmoid(z)print('loss: ', self.__loss(h, y))def predict_prob(self, X):if self.fit_intercept:X = self.__add_intercept(X)return sigmoid(np.dot(X, self.theta))def predict(self, X, threshold=0.5):return self.predict_prob(X) >= threshold
3. 训练模型
现在,我们可以通过调用LogisticRegression类来训练模型。我们将样本分成训练集和测试集,使用训练集来训练模型,并使用测试集来评估模型性能。
from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)model = LogisticRegression(lr=0.1, num_iter=300000)
model.fit(X_train, y_train)print('Training accuracy:', (model.predict(X_train) == y_train).mean())
print('Test accuracy:', (model.predict(X_test) == y_test).mean())
输出:

4. 结果可视化
最后,我们可以将模型的决策边界可视化。由于我们只使用了两个特征,所以决策边界是一条直线。
import matplotlib.pyplot as pltplt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='viridis')x1_min, x1_max = X[:, 0].min(), X[:, 0].max(),
x2_min, x2_max = X[:, 1].min(), X[:, 1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red')
输出:
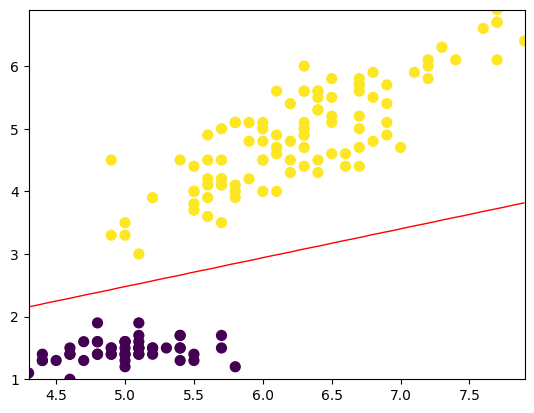
这个实例展示了如何使用Logistic回归算法来解决二分类问题。通过加载鸢尾花数据集,选择两个特征并标记两个类别,我们定义了LogisticRegression类来训练和预测模型。在这个简单的示例中,模型在训练集和测试集上都得到了100%的准确度,说明模型具有很好的适应能力和泛化能力。
需要注意的是,在实际应用中,需要考虑更多的因素,例如数据集的大小、特征的选择、模型的超参数等等。此外,在使用Logistic回归模型时,还需要进行特征缩放、正则化等处理,以提高模型的性能和泛化能力。
结语
Logistic回归是一种简单而有效的二元分类算法,它通过逻辑函数将线性回归的预测值转换为概率值。在实际应用中,Logistic回归通常与其他算法(如决策树和随机森林)结合使用,以提高分类的准确率。它也可以通过特征工程和正则化等方法进行改进,以适应不同的数据集和问题。同时,根据实际情况选择适当的激活函数,在解决其他分类问题时也是非常重要的。
希望这篇博客对你有所帮助!如果你有任何问题或疑惑,欢迎在下方留言讨论。
相关文章:

探究Logistic回归:用数学解释分类问题
文章目录 前言回归和分类Logistic回归线性回归Sigmoid函数把回归变成分类Logistic回归算法的数学推导Sigmoid函数与其他激活函数的比较 Logistic回归实例1. 数据预处理2. 模型定义3. 训练模型4. 结果可视化 结语 前言 当谈论当论及机器学习中的回归和分类问题时,很…...

杨辉三角
打印n行杨辉三角,n<10。 输入格式: 直接输入一个小于10的正整数n。 输出格式: 输出n行杨辉三角,每个数据输出占4列。 输入样例: 5输出样例: 11 11 2 11 3 3 11 4 6 4 1代码长度限制 16 KB 时间限制 400 ms 内存限制 6…...
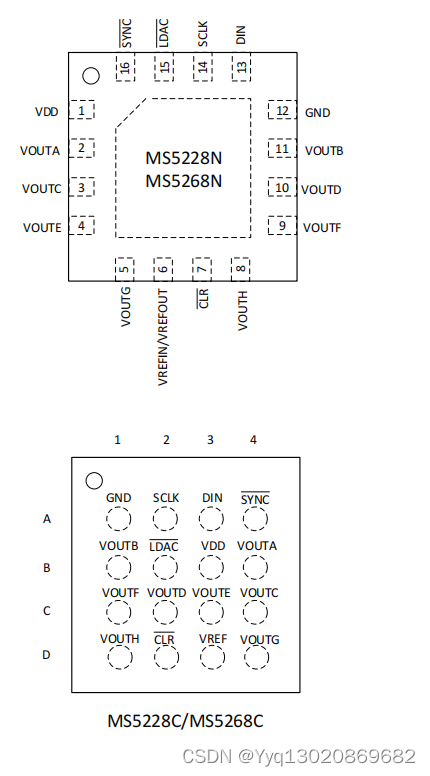
MS5228/5248/5268:2.7V 到 5.5V、 12/14/16Bit、内置基准、八通道数模转换器
MS5228/MS5248/MS5268 是一款 12/14/16bit 八通道输出的电压型 DAC ,内部集成上电复位电路、可选内部基准、接口采用四线串口模式, 最高工作频率可以到 40MHz ,可以兼容 SPI 、 QSPI 、 DSP 接口和 Microwire 串口。输出接到一个 …...

2024年江苏省职业院校技能大赛 信息安全管理与评估 第二阶段教师组 (样卷)
2024年江苏省职业院校技能大赛 信息安全管理与评估 第二阶段教师组 (样卷) 项目竞赛样题 本文件为信息安全管理与评估项目竞赛-第二阶段样题,内容包括:网络安全事件响应、数字取证调查、应用程序安全。 本次比赛时间为180分钟。 介绍 GeekSec专注技能竞…...
最新版IDEA专业版大学生申请免费许可证教学(无需学校教育邮箱+官方途径+非破解手段)
文章目录 前言1. 申请学籍在线验证报告2. 进入IDEA官网进行认证3. 申请 JB (IDEA) 账号4. 打开 IDEA 专业版总结 前言 当你进入本篇文章时, 你应该是已经遇到了 IDEA 社区版无法解决的问题, 或是想进一步体验 IDEA 专业版的强大. 本文是一篇学生申请IDEA免费许可证的教学, 在学…...

zookeeper常用接口
ZookeeperTemplate 是 Spring Cloud Zookeeper 中的一个重要类,它提供了一组方便的方法来操作 Zookeeper,例如创建节点、获取节点数据、删除节点等。下面列举了 ZookeeperTemplate 的一些常用方法及其作用: createExclusive(String path):创建独占节点。如果节点已经存在,…...
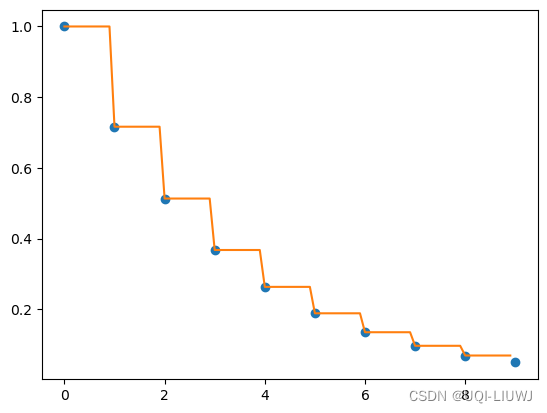
scipy笔记:scipy.interpolate.interp1d
1 主要使用方法 class scipy.interpolate.interp1d(x, y, kindlinear, axis-1, copyTrue, bounds_errorNone, fill_valuenan, assume_sortedFalse) 2 主要函数 x一维实数值数组,代表插值的自变量y N维实数值数组,其中沿着插值轴的 y 长度必须等于 x 的…...

外包干了一个月,技术明显进步。。。。。
先说一下自己的情况,本科生生,19年通过校招进入南京某软件公司,干了接近2年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了2年的功能测试…...

docker安装node及使用
文章目录 一、安装node二、创建node容器三、进入创建的容器如有启发,可点赞收藏哟~ 一、安装node 查看可用版本 docker search node安装最新版本 docker install node:latest二、创建node容器 docker run -itd --name node-test node–name node-test࿱…...

要求CHATGPT高质量回答的艺术:提示工程技术的完整指南—第 18 章:对抗性提示
要求CHATGPT高质量回答的艺术:提示工程技术的完整指南—第 18 章:对抗性提示 对抗性提示是一种允许模型生成能够抵御某些类型的攻击或偏差的文本的技术。这种技术可用于训练更健壮、更能抵御某些类型的攻击或偏差的模型。 要在 ChatGPT 中使用对抗性提…...

若依框架的搭建
若依框架 若依框架的搭建(前后端分离版本)环境要求IDEA拉取Gitee源码Mysql 配置Redis 配置后端启动前端配置问题解决 效果展示 若依框架的搭建(前后端分离版本) 简介 RuoYi-Vue 是一个 Java EE 企业级快速开发平台,基…...
SQL Server 数据库,多表查询
4.2使用T-SQL实现多表查询 前面讲述过的所有查询都是基于单个数据库表的查询,如果一个查询需要对多个表进行操作, 就称为联接查询,联接查询的结果集或结果称为表之间的联接。 联接查询实际上是通过各个表之间共同列的关联性来查询数据的&…...

程序解释与编译
▶1.程序的解释执行方式 程序语言强写的计策机指令序列称为“源程序”,计算机并不能直接执行用高级语言编写的源程序,源程序必须通过“翻译程序”翻译成机器指令的形式,计算机才能项别和执行。源程序的翻译有两种方式:解释执行和编译执行。不…...

聊聊 Jetpack Compose 的 “状态订阅自动刷新” -- mutableStateListOf
Jekpack Compose “状态订阅&自动刷新” 系列: 【 聊聊 Jetpack Compose 的 “状态订阅&自动刷新” - - MutableState/mutableStateOf 】 【 聊聊 Jetpack Compose 的 “状态订阅&自动刷新” - - remember 和重组作用域 】 【 聊聊 Jetpack Compose 的 …...

Dockerfile详解#如何编写自己的Dockerfile
文章目录 前言编写规则指令详解FROM:基础镜像LABEL:镜像描述信息MAINTAINER:添加作者信息COPY:从宿主机复制文件到镜像中ADD:从宿主机复制文件到镜像中WORKDIR:设置工作目录 前言 Dockerfile是编写docker镜…...

Elasticsearch桶聚合和管道聚合
1. 根据名称统计数量 GET order/_search {"_source": false,"aggs": {"aggs_name": { // 自定义查询结果名称"terms": { // 使用的函数"field": "name.keyword"}}} }查询结果例子: "aggregat…...

联想范建平:联想混合AI架构具备两大明显优势
12月7日,首届AI PC创新论坛在北京联想集团总部举办。联想集团副总裁、联想研究院人工智能实验室负责人范建平表示,为提供真正可信、个性化的AI专属服务,联想提出了混合智能(Hybrid AI)概念,并已经显现出更强…...

探索Spring事件监听机制的奇妙世界
文章目录 什么是Spring事件监听机制主要组件内置的事件监听类自定义事件监听类总结 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 什么是Spring事件监听机制 Spring事件监听机制是Spr…...

什么是散列函数
散列函数是一种公开的数学函数。散列函数运算的输入信息也可叫作报文。散列函数运算后所得到的结果叫作散列码或者叫作消息摘要。散列函数具有如下一些特点: (1)不同内容的报文具有不同的散列码,而一旦原始报文有任何改变…...

tomcat反序列化
漏洞介绍: 漏洞名称: Apache Tomcat反序列化漏洞影响范围: Apache Tomcat服务器中使用了自带session同步功能的配置,且没有使用Encrypt Interceptor加密拦截器的情况下。漏洞描述: Apache Tomcat是一个基于Java的Web应用软件容器,用于运行servlet和JSP Web应用。当Tomc…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
