面试遇到的一些问题(二)
1、v-if v-show 区别,他们的生命周期区别
v-show: (类似于display:none/black 的切换)不管初始值是true 或false 都会进行渲染,状态改变也不会销毁和重新生成。不会影响生命周期
v-if : 是根据条件,dom进行删除插入操作。
依附于普通元素时:会触发父组件的beforeUpdate和updated
依附于组件时:对父组件的影响也是触发beforUpdate,updated
对自身的影响:false-true: beforeCreate,created,beforMount,mounted,
true-false: beforeDestroy(销毁前), destroyed(销毁后)
2、map() 和forEach() 区别
返回值不同-map()会返回一个新的数组,forEach() 会改变原数组,并且它的返回值是undefined
适用场景:map()常常更适用于,给它的每一项元素应用一个函数时。forEach()更常用于不打算改变数据值的时候。
3、vuex 有什么办法可以永久存储
在页面mouted(挂载后)的钩子函数中监听页面的window的unload(重载)事件——然后再每次页面刷新时将数据保存到sessionStroge
4、vuex 与localStorage\sessionStorage区别
- vuex 刷新
相关文章:
)
面试遇到的一些问题(二)
1、v-if v-show 区别,他们的生命周期区别 v-show: (类似于display:none/black 的切换)不管初始值是true 或false 都会进行渲染,状态改变也不会销毁和重新生成。不会影响生命周期 v-if : 是根据条件,dom进行删除插入操作。 依附于普通元素时:会触发父组件的beforeUpdate和u…...
JDK8新特性:Lambda表达式规则及用法,方法引用
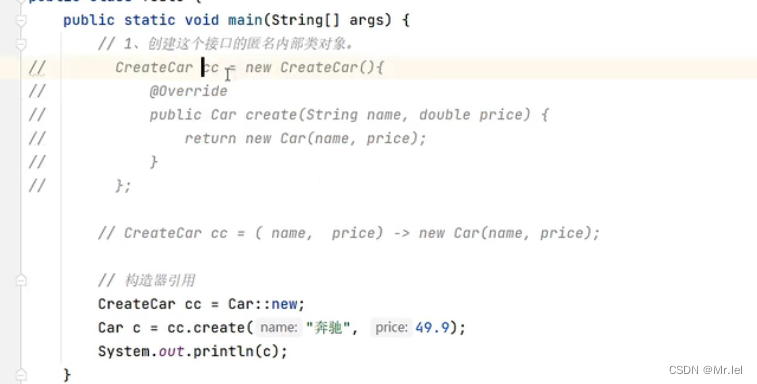
目录 Lambda表达式是JDK8新增的一种语法格式 1.作用 2.用法规则: 3.方法引用 Lambda表达式是JDK8新增的一种语法格式 1.作用 简化匿名内部类的代码写法 Lambad用法前提:只能简化函数式接口(一般加有Funcationallnterface)&a…...
【GIS】JDK版本升级到17后,GeoServer的图层无法通过openLayer预览
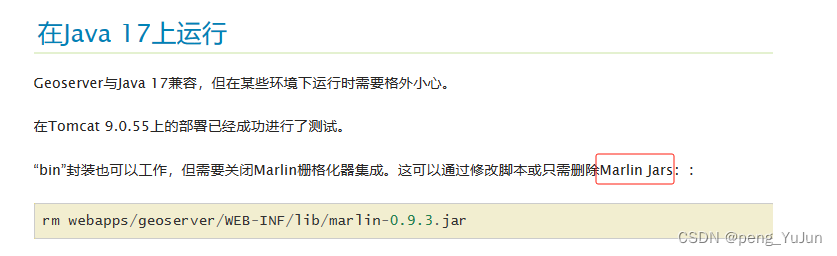
JDK版本升级到17后,图层无法通过openLayer预览 1. 错误图示 终端输出的错误 网页端无法显示图层,并且输出错误提示 2.原因猜测 估计可能是由于java17的模块化,Java被分成了多个独立部署和运行的模块,这使得Java应用能够更快…...

vue 批量下载文件,不走后端接口的方法
今天ld提了一个需求,说页面的列表里面有要下载的地址,然后点击批量下载。我思索片刻,给出了代码 1.这个是列表页面的代码 <!-- 这个是列表页面的代码 --> <el-table :data"userListShow" align"center"border highlight-…...

科技云报道:AI+PaaS,中国云计算市场迎来新“变量”?
科技云报道原创。 没有小的市场,只有还没有被发现的大生意。 随着企业数字化转型的逐级深入,市场需求进一步向PaaS和SaaS层进发,使之成为公有云服务市场增长的主要动力。 根据IDC最新发布的报告显示,2022-2027五年间中国公有云…...
Windows Service Name重复问题
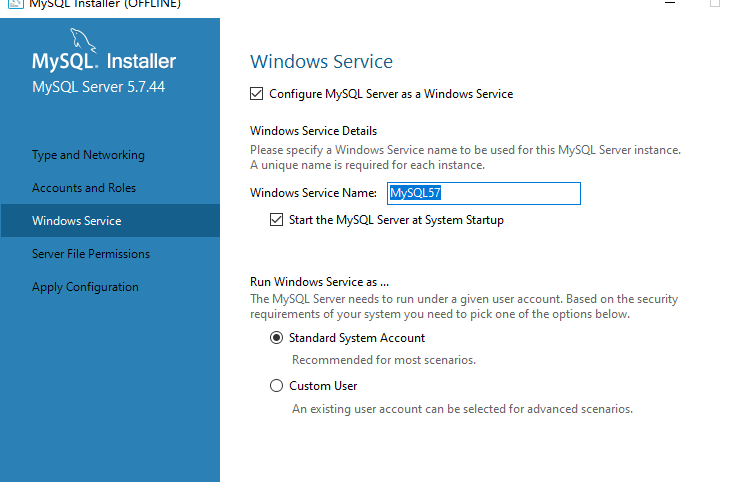
Windows Service Name重复问题 1,问题 2,打开命令提示符,管理员身份运行 3,输入命令:sc delete MYSQL57 4,验证一下,可以看见已经没有感叹号啦 ,可以看见已经没有感叹号啦...

BBS项目
一.BBS项目介绍 1.项目开发流程 项目立项 ------> 公司高层决定需求调研和分析 ------> 市场人员,技术人员参与 -需求文档说明开发部门开会 ------> 确定项目架构,技术选型,数据库设计UI,UD团队(产品经…...
)
Java基础——对象类型转换(向上、向下转型)
非继承关系的类之间对象类型不可以互相类型转换,只有继承关系才可以互相转换。 简单说,对象类型转换的前提要是继承关系。 对象类型转换分为:向上转型和向下转型。多态就是一种自动向上转型。 向上转型:子类对象用父类类型接收…...
期末速成数据库极简版【查询】(2)
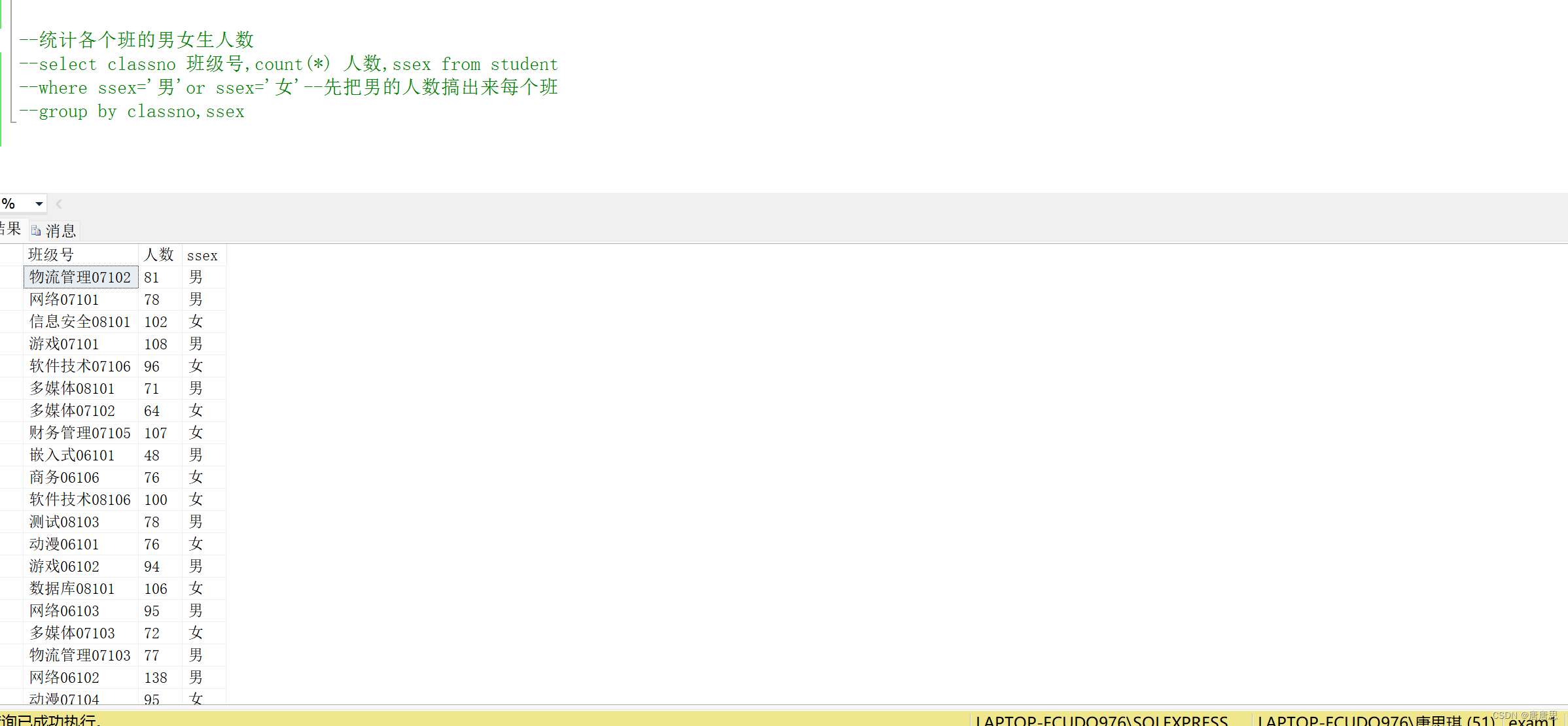
目录 select数据查询----表 【1】筛选列 【2】where简单查询 【3】top-n/distinct/排序的查询 【4】常用内置函数 常用日期函数 常用的字符串函数 【5】模糊查询 【6】表数据操作——增/删/改 插入 更新 删除 【7】数据汇总 聚合 分类 🙂&#…...

2023年终总结-轻舟已过万重山
自我介绍 高考大省的读书人 白,陇西布衣,流落楚、汉。-与韩荆州书 我来自孔孟故里山东济宁,也许是小学时的某一天,我第一次接触到了电脑,从此对它产生了强烈的兴趣,高中我有一个愿望:成为一名计…...

手机号,邮箱,密码,验证码正则表达式[Java]
Util类: public abstract class RegexPatterns {/*** 手机号正则*/public static final String PHONE_REGEX "^1([38][0-9]|4[579]|5[0-3,5-9]|6[6]|7[0135678]|9[89])\\d{8}$";/*** 邮箱正则*/public static final String EMAIL_REGEX "^[a-zA-Z…...
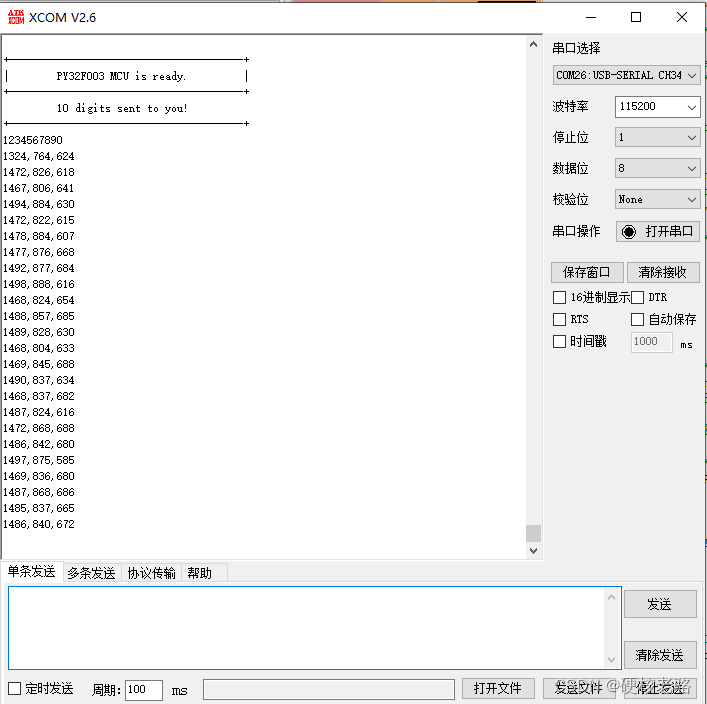
普冉(PUYA)单片机开发笔记(7): ADC-轮询式多路采样
概述 应用中经常会有使用单片机进行模数转换的需求。PY32F003 具有 1 个 12 位的模拟数字转换器(ADC),今天我们一起来使用一下这个 ADC。 数据手册中对 ADC 简介如下。 SAR ADC:逐次逼近式 ADC,原理参见“参考链接&a…...

uniapp切换页面时报错问题
我们来看如下错误: 该错误的意思是不能切换到 tabbar 页面。tabbar页面通常是公共页面或者底部导航栏,如果我们用 navigateTo 或者 redirectTo 都不能实现页面切换。 我们有两种方式: 第一种是用 switchTab 来进行切换,但注意切…...
Nginx 简单入门操作
前言:之前的文章有些过就不罗嗦了。 Nginx 基础内容 是什么? Nginx 是一个轻量级的 HTTP 服务器,采用事件驱动、异步非阻塞处理方式的服务器,它具有极好的 IO 性能,常用于 HTTP服务器(包含动静分离)、正向代理、反向代理、负载均衡 等等. Nginx 和 Node.js 在很多方…...

ChatGPT是科学还是艺术?
OpenAI最近谈到GPT4变懒的问题,说“它更像是多人共同参与的艺术创作”,那到底大模型是科学还是艺术?...
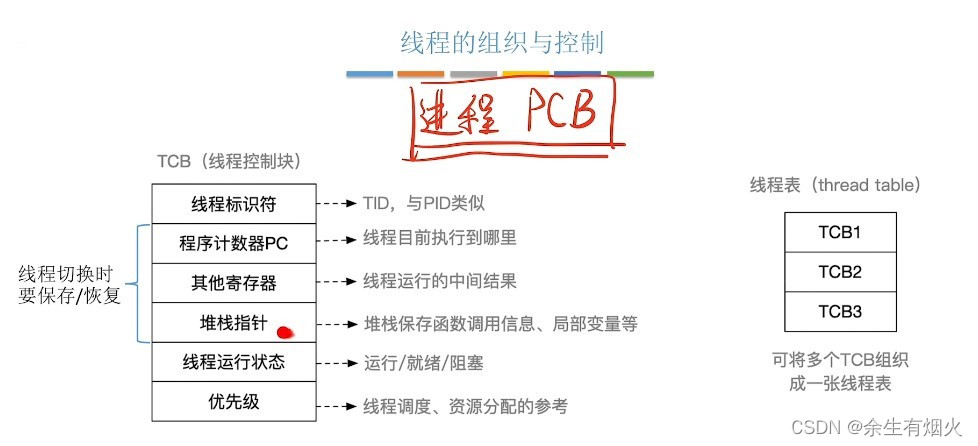
线程及实现方式
一、线程 线程是一个基本的CPU执行单元,也是程序执行流的最小单位。引入线程之后,不仅是进程之间可以并发,进程内的各线程之间也可以并发,从而进一步提升了系统的并发度,使得一个进程内也可以并发处理各种任务&#x…...

2023年11月10日 Go生态洞察:十四年Go的成长之路
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

OpenSSL 编程指南
目录 前言初始化SSL库创建SSL 上下文接口(SSL_CTX)安装证书和私钥加载证书(客户端/服务端证书)加载私钥/公钥加载CA证书设置对端证书验证例1 SSL服务端安装证书例2 客户端安装证书创建和安装SSL结构建立TCP/IP连接客户端创建socket服务端创建连接创建SSL结构中的BIOSSL握手服务…...

js优化技巧
一、使用箭头函数简化函数定义 function add(a,b){return a b; }//箭头函数 const add (a,b) > a b;二、使用解构赋值简化变量声明 const firstName person.firstName; const lastName person.lastName;//解构赋值 const {firstName,lastName} person三、使用模板字…...

深入探索 Java 反射机制
文章目录 什么是 Java 反射?反射的核心类和接口反射的基本用法获取 Class 对象的三种方式创建对象实例访问字段和方法调用构造方法 反射的使用场景注意事项结语 Java反射(Reflection)是指在运行时获取类的信息,特别是获取其属性、…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
