20231210 随机矩阵和M矩阵
1. 非负矩阵:矩阵元素均非负
定义 7.1.1 设 A = ( a i j ) ∈ R m × n \boldsymbol{A}=\left(a_{i j}\right) \in \mathbb{R}^{m \times n} A=(aij)∈Rm×n, 如果
a i j ⩾ 0 , i = 1 , ⋯ , m ; j = 1 , ⋯ , n , a_{i j} \geqslant 0, \quad i=1, \cdots, m ; j=1, \cdots, n, aij⩾0,i=1,⋯,m;j=1,⋯,n,
即 A \boldsymbol{A} A 的所有元素是非负的, 则称 A \boldsymbol{A} A 为非负矩阵, 记作 A ⩾ 0 \boldsymbol{A} \geqslant 0 A⩾0; 若式 (7.1.1) 中严格不等号成立, 即 a i j > 0 ( i = 1 , ⋯ , m ; j = 1 , ⋯ , n ) a_{i j}>0(i=1, \cdots, m ; j=1, \cdots, n) aij>0(i=1,⋯,m;j=1,⋯,n), 则称 A \boldsymbol{A} A 为正矩阵, 记为 A > 0 \boldsymbol{A}>0 A>0.
2. 随机矩阵:
定义 7.2.1 设 A = ( a i j ) ∈ R n × n \boldsymbol{A}=\left(a_{i j}\right) \in \mathbb{R}^{n \times n} A=(aij)∈Rn×n 是非负矩阵, 如果 A \boldsymbol{A} A 的每一行上的元素之和都等于 1 , 即
∑ j = 1 n a i j = 1 , i = 1 , 2 , ⋯ , n , \sum_{j=1}^n a_{i j}=1, \quad i=1,2, \cdots, n, j=1∑naij=1,i=1,2,⋯,n,
则称 A \boldsymbol{A} A 为随机矩阵; 如果 A \boldsymbol{A} A 还满足
∑ i = 1 n a i j = 1 , j = 1 , 2 , ⋯ , n , \sum_{i=1}^n a_{i j}=1, \quad j=1,2, \cdots, n, i=1∑naij=1,j=1,2,⋯,n,
则称 A \boldsymbol{A} A 为双随机矩阵.
定理 7.2.1 设 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n 是随机矩阵,则有
ρ ( A ) = 1. \rho(\boldsymbol{A})=1 . ρ(A)=1.
证明:谱半径 ρ \rho ρ 是矩阵最大特征值。因为 A \boldsymbol{A} A 是随机矩阵, 所以 A \boldsymbol{A} A 的每一行元素之和为 1 , 则 ∥ A ∥ ∥ ∞ = 1 \|\boldsymbol{A}\| \|_{\infty}=1 ∥A∥∥∞=1. 令 x = ( 1 , ⋯ , 1 ) T \boldsymbol{x}=(1, \cdots, 1)^{\mathrm{T}} x=(1,⋯,1)T, 显然 A x = x = ∥ A ∥ ∞ x \boldsymbol{A} \boldsymbol{x}=\boldsymbol{x}=\|\boldsymbol{A}\|_{\infty} \boldsymbol{x} Ax=x=∥A∥∞x, 即 x \boldsymbol{x} x 是 A \boldsymbol{A} A 对应于特征值 ∥ A ∥ ∞ \|\boldsymbol{A}\| \infty ∥A∥∞ 的特征向量, 而 ρ ( A ) ⩽ ∥ A ∥ ∞ \rho(\boldsymbol{A}) \leqslant\|\boldsymbol{A}\|_{\infty} ρ(A)⩽∥A∥∞, 同时又有 ∥ A ∥ ∞ ⩽ ρ ( A ) \|\boldsymbol{A}\|_{\infty} \leqslant \rho(\boldsymbol{A}) ∥A∥∞⩽ρ(A), 故得 ρ ( A ) = ∥ A ∥ ∞ = 1 \rho(\boldsymbol{A})=\|\boldsymbol{A}\|_{\infty}=1 ρ(A)=∥A∥∞=1.
证毕
定理 7.2.2 随机矩阵的乘积仍为随机矩阵。
闵可夫斯基(Minkovski)矩阵,简称M矩阵
定义 7.4.1 设 A ∈ R n × n A \in \mathbb{R}^{n \times n} A∈Rn×n, 且可表示为
A = s I − B , s > 0 , B ⩾ 0. \boldsymbol{A}=s \boldsymbol{I}-\boldsymbol{B}, \quad s>0, \quad \boldsymbol{B} \geqslant 0 . A=sI−B,s>0,B⩾0.
若 s ⩾ ρ ( B ) s \geqslant \rho(\boldsymbol{B}) s⩾ρ(B), 则称 A \boldsymbol{A} A 为 M \mathbf{M} M 矩阵; 若 s > ρ ( B ) s>\rho(\boldsymbol{B}) s>ρ(B), 则称 A \boldsymbol{A} A 为非奇异 M \mathbf{M} M 矩阵.
Q:为什么叫非奇异M矩阵?
A:因为M矩阵的每一个实特征值均为正。 ( s I − B ) x A = λ A x A (s\boldsymbol{I}-\boldsymbol{B})\boldsymbol{x}_A=\lambda_A\boldsymbol{x}_A (sI−B)xA=λAxA, λ A \lambda_A λA 和 x A \boldsymbol{x}_A xA 分别为矩阵 A \boldsymbol{A} A 的特征值和特征向量。那么 B x A = ( s − λ A ) x A \boldsymbol{B}\boldsymbol{x}_A=(s-\lambda_A)\boldsymbol{x}_A BxA=(s−λA)xA。反证法:加入 λ A \lambda_A λA为负数,那么 s − λ A > s > ρ ( B ) s-\lambda_A>s>\rho(\boldsymbol{B}) s−λA>s>ρ(B),上述等式不可能成立。因此 λ A \lambda_A λA为正数。
相关文章:

20231210 随机矩阵和M矩阵
1. 非负矩阵:矩阵元素均非负 定义 7.1.1 设 A ( a i j ) ∈ R m n \boldsymbol{A}\left(a_{i j}\right) \in \mathbb{R}^{m \times n} A(aij)∈Rmn, 如果 a i j ⩾ 0 , i 1 , ⋯ , m ; j 1 , ⋯ , n , a_{i j} \geqslant 0, \quad i1, \cdots, m ; j1, \cd…...
Linux(centos)学习笔记(初学)
[rootlocalhost~]#:[用户名主机名 当前所在目录]#超级管理员标识 $普通用户的标识 Ctrlshift放大终端字体 Ctrl缩小终端字体 Tab可以补全命令 Ctrlshiftc/V复制粘贴 / :根目录,Linux系统起点 ls: #list列出目录的内容,通常用户查看…...

ECharts标题字体大小自适应变化
我们在做自适应Echarts的时候,字体大小在配置项里是如下配置的, title 标题组件,包含主标题和副标题。 以下是常用的对标题的设置: title:{//设置图表的标题text:"主标题",link:"baidu.com", //设置标题超链接target:"self",...
解决使用pnpm安装时Sharp模块报错的方法
在使用pnpm进行项目依赖安装的过程中,有时候会遇到Sharp模块报错的情况。Sharp是一个用于处理图像的Node.js模块,但它的安装可能会因为各种原因而失败,导致项目无法正常启动。本文将介绍这个问题的方法。 问题描述 解决方法 在命令行分别输…...

Redis 数据的持久化 RDB、AOF、RDB + AOF、No persistence 各自优缺点
文章目录 一、RDB (Redis Database)1.1 RDB 优势1.2 RDB 缺点1.3 RDB 如何工作1.4 RDB配置1.5 开启/关闭,RDB快照策略,save指令1.6 持久化硬盘文件,dbfilename指令1.7 持久化硬盘文件的存储地址,dir指令 二、AOF (Append Only Fil…...
回味童年经典游戏的项目
目录 1.超级玛丽2.坦克大战3.吃豆人游戏4.贪吃蛇游戏 1.超级玛丽 项目地址:超级马里奥游戏源码 在线试玩网址在资源描述中 在线试玩:http://martindrapeau.github.io/backbone-game-engine/super-mario-bros/index.html 主要语言:JavaScript…...

Electron[5] 渲染进程和主进程
1 进程 Electron里头的进程分为渲染进程和主进程。简单理解: main.js就是主进程每个页面就是渲染进程一个Electron应用仅有一个主进程,可以有多个渲染进程 上面的这些概念很重要,不展开细讲。 2 进程职责 主进程是用来实现应用的基础功能…...
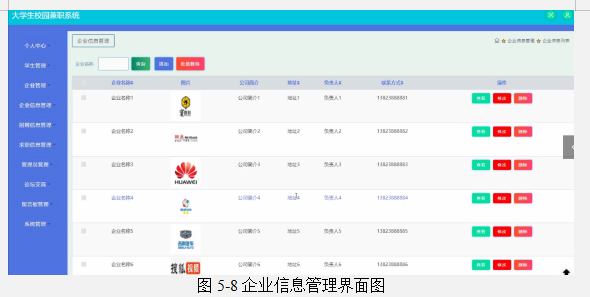
基于Java SSM框架实现大学生校园兼职系统项目【项目源码+论文说明】
基于java的SSM框架实现大学生兼职系统演示 摘要 随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,大学生校园兼职系统当然也不能排除在外。大学生校园兼职系统是以实际运用为开…...
Codeforces Round 913 (Div. 3) A~E
目录 A. Rook 问题分析: B. YetnotherrokenKeoard 问题分析: C. Removal of Unattractive Pairs 问题分析: D. Jumping Through Segments 问题分析: E. Good Triples 问题分析: A. Rook 问题分析: 给一个棋子将其同行同列的位置输出 #include<bits/s…...

反序列化 [网鼎杯 2020 朱雀组]phpweb 1
打开题目 我们发现这个页面一直在不断的刷新 我们bp抓包一下看看 我们发现index.php用post方式传了两个参数上去,func和p 我们需要猜测func和p两个参数之间的关系,可以用php函数MD5测一下看看 我们在响应处得到了一串密文,md5解密一下看看 发…...
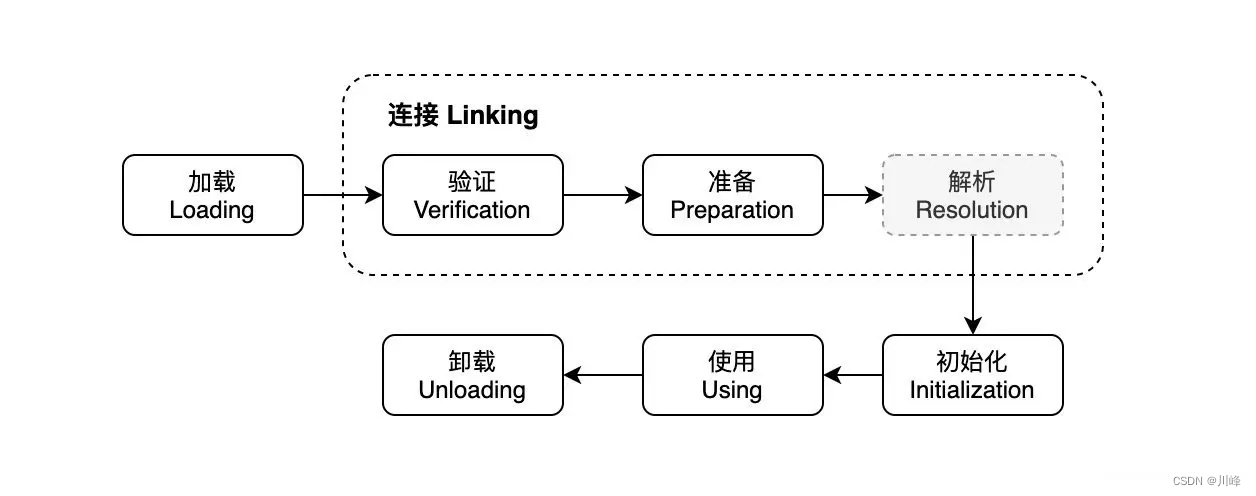
Java 何时会触发一个类的初始化
Java 何时会触发一个类的初始化? 使用new关键字创建对象访问类的静态成员变量 或 对类的静态成员变量进行赋值调用类的静态方法反射调用类时,如 Class.forName()初始化子类时,会先初始化其父类(如果父类还没有进行过初始化的话&a…...

我的记事本
url uniform resource locator. 统一资源定位符 请求状态码 1XX:信息响应 2XX:成功响应 3XX:重定向消息 4XX:客户端错误响应 5XX:服务器端错误响应 IP地址分类 本机回环IP地址:127.0.0.1 ~ 127.255.255.254 局域网IP(私网IP) 192.168.0.0 &am…...
)
GO设计模式——4、单例模式(创建型)
目录 单例模式(Singleton Pattern) 优缺点 使用场景 饿汉式和懒汉式单例模式 单例模式(Singleton Pattern) 单例模式(Singleton Pattern)是一个类只允许创建一个对象(或者实例ÿ…...

我对迁移学习的一点理解——领域适应(系列3)
文章目录 1. 领域适应(Domain Adaptation)的基本概念2.领域适应(Domain Adaptation)的目标3.领域适应(Domain Adaptation)的实现方法4.领域适应(Domain Adaptation)的可以解决的问题…...
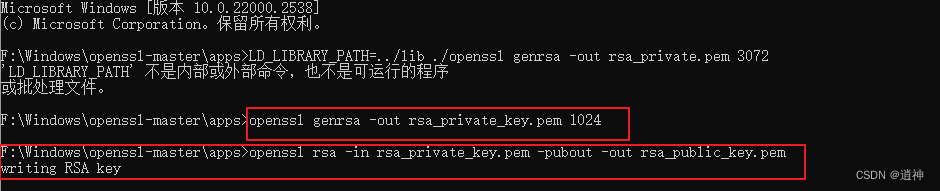
【openssl】RSA 生成公钥私钥 |通过私钥获取公钥
通过博客:Window系统如何编译openssl 编译出openssl.exe(位于apps文件夹下)。 现在需要使用它获得公钥私钥、通过私钥获取公钥 目录 说明!!! 一.定位openssl.exe目录 二、进入命令cmd 三、生成私钥 …...

MongoDB的删除文档、查询文档语句
本文主要介绍MongoDB的删除文档、查询文档命令语句。 目录 MongoDB删除文档MongoDB查询文档 MongoDB删除文档 MongoDB是一种基于文档的NoSQL数据库,它使用BSON格式存储文档。删除文档是MongoDB数据库中的常见操作之一。 下面是MongoDB删除文档的详细介绍和示例&am…...
-trait)
Rust编程语言入门教程(三)-trait
文章目录 Rust编程语言入门教程(三)-trait什么是 trait?trait使用举例 Rust编程语言入门教程(三)-trait 什么是 trait? trait 是 Rust 中的接口,它定义了类型使用这个接口的行为。你可以类比到…...

LeetCode-1566. 重复至少 K 次且长度为 M 的模式【数组 枚举】
LeetCode-1566. 重复至少 K 次且长度为 M 的模式【数组 枚举】 题目描述:解题思路一:题意就是找出长度为m且连续重复k次的子数组。解题思路就是暴力枚举加剪枝。解题思路二:思路差不多解题思路三:0 题目描述: 给你一个…...
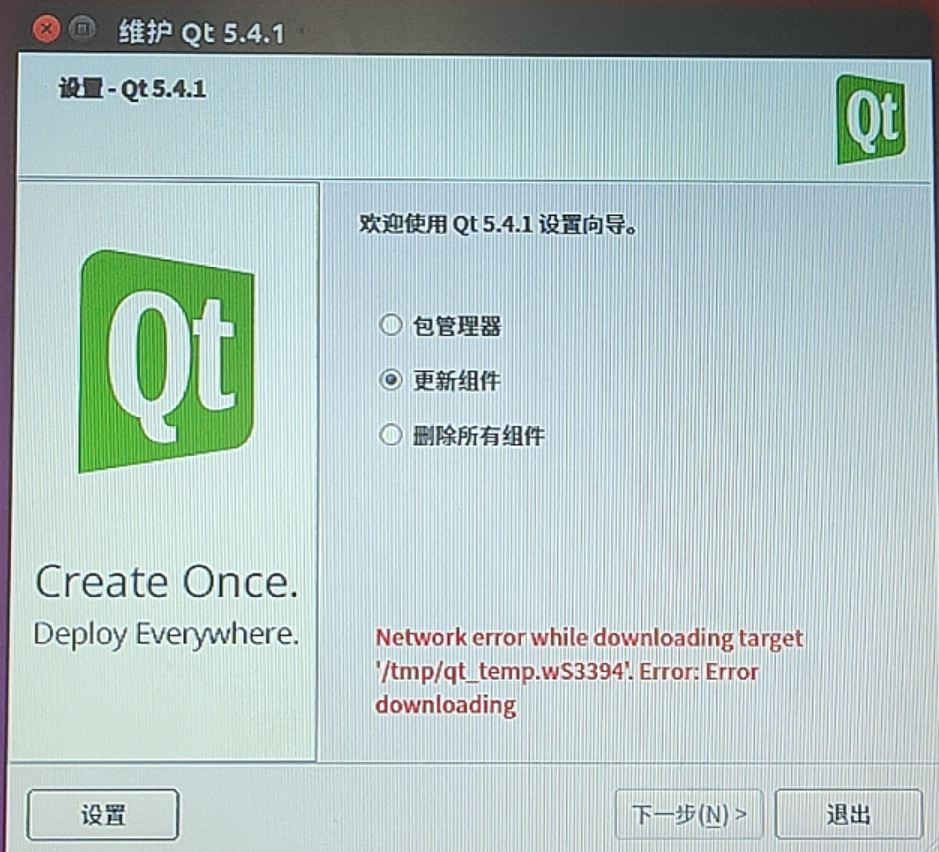
QT5.4.1无法打开文件
问题描述:起初是在QT代码中运行打开文件代码: QString gFilename QFileDialog::getOpenFileName(this,"open File",path,"*", nullptr,QFileDialog::DontUseNativeDialog);时,出现了堵塞情况,经过多次实验一…...

【1day】金和OA某接口存在未授权访问漏洞
注:该文章来自作者日常学习笔记,请勿利用文章内的相关技术从事非法测试,如因此产生的一切不良后果与作者无关。 目录 一、漏洞描述 二、影响版本 三、资产测绘 四、漏洞复现...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
