784. 字母大小写全排列
字母大小写全排列
描述 :
给定一个字符串 s ,通过将字符串 s 中的每个字母转变大小写,我们可以获得一个新的字符串。
返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。
题目 :
LeetCode 784.字母大小写全排列 :
784. 字母大小写全排列

分析 :
如果本题去掉数字,只告诉你两个字母ab,让你每个字母变化大小写,那就是ab、Ab、aB、AB四种情况,题目比2.6电话号码问题还简单,这里的数字就是干扰项,我们需要做的是过滤掉数字,只处理字母另外还要添加个大小写转换的问题。
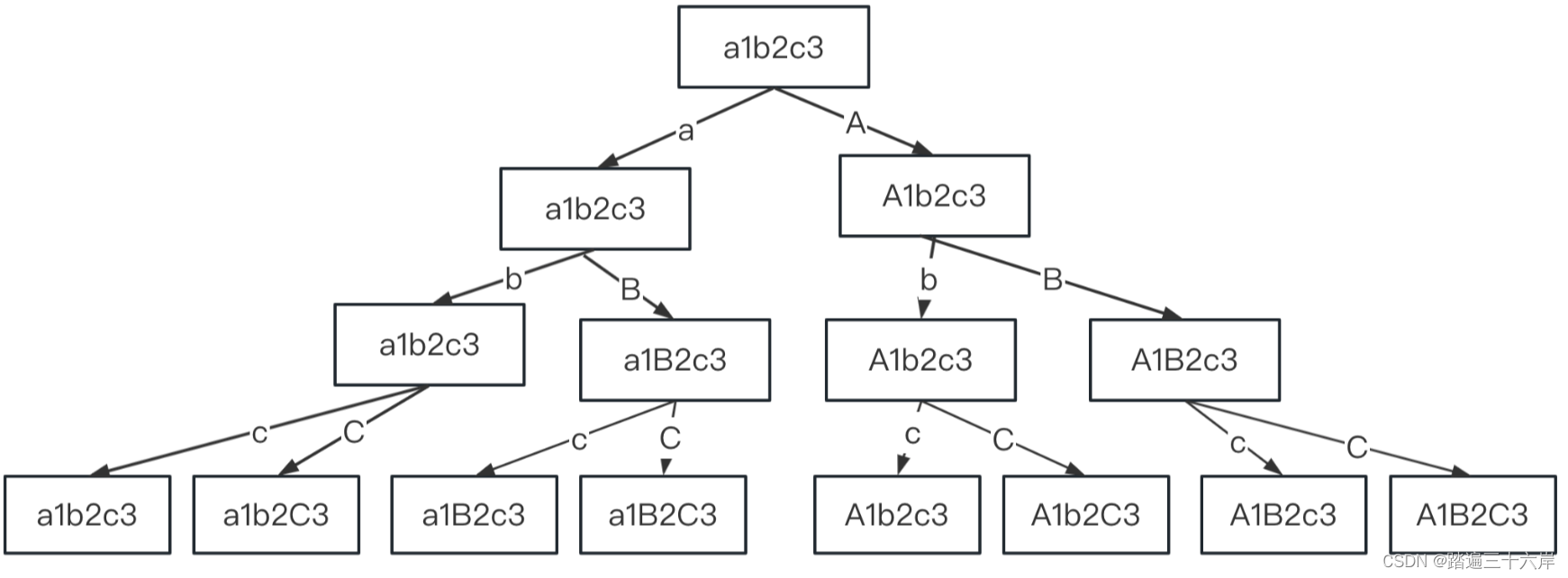
由于每个字符的大小写形式刚好差了32,因此在大小写装换时可以用c32 来进行转换和恢复。
解析 :
class Solution {List<String> list = new ArrayList<>();public List<String> letterCasePermutation(String s) {char[] arr = s.toCharArray();dfs(arr,0);return list;}public void dfs(char[] arr,int start){while(start < arr.length && Character.isDigit(arr[start])){start++;}if(start == arr.length){list.add(new String(arr));return;}arr[start] ^= 32;dfs(arr,start + 1);arr[start] ^= 32;dfs(arr,start + 1);}
}相关文章:

784. 字母大小写全排列
字母大小写全排列 描述 : 给定一个字符串 s ,通过将字符串 s 中的每个字母转变大小写,我们可以获得一个新的字符串。 返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。 题目 : LeetCode 784.字母大小写全排列 : 784. 字母大小写全排列 分析…...
HarmonyOS鸿蒙应用开发——HTTP网络访问与封装
文章目录 基本使用封装参考 基本使用 鸿蒙应用发起HTTP请求的基本使用,如下: 导入http模块创建httpRequest对象发起http请求,并处理响应结果 第一、导入http模块: import http from ohos.net.http第二、创建httpRequest对象&a…...

vscode 编写爬虫爬取王者荣耀壁纸
网上关于爬虫大部分教程和编辑器用的都不是vscode ,此教程用到了vscode、Python、bs4、requests。 vscode配置Python安装环境可以看看这个大佬的教程 03-vscode安装和配置_哔哩哔哩_bilibili vscode配置爬虫环境可以参考这个大佬的教程【用Vscode实现简单的python…...

spring boot + uniapp 微信公众号 jsapi 支付
后端支付类 package com.ruoyi.coupon.payment;import com.google.gson.Gson; import com.ruoyi.coupon.payment.dto.PayParamJsapiDto; import com.ruoyi.coupon.payment.dto.RefundParam; import com.ruoyi.coupon.service.ICouponConfigService; import com.wechat.pay.jav…...

【数学建模】《实战数学建模:例题与讲解》第九讲-时间序列分析(含Matlab代码)
【数学建模】《实战数学建模:例题与讲解》第九讲-时间序列分析(含Matlab代码) 基本概念确定性时间序列分析方法平稳时间序列模型ARIMA模型季节性序列 习题8.11. 题目要求2.解题过程3.程序4.结果 习题8.21. 题目要求2.解题过程3.程序4.结果 习…...
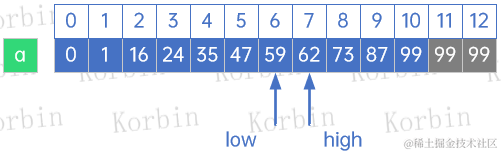
大话数据结构-查找-有序表查找
注:本文同步发布于稀土掘金。 3 有序表查找 3.1 折半查找 折半查找(Binary Search)技术,又称为二分查找,它的前提是线性表中的记录必须是关键码有序(通常从小到大有序),线性表必须…...

Qt实现二维码生成和识别
一、简介 QZxing开源库: 生成和识别条码和二维码 下载地址:https://gitcode.com/mirrors/ftylitak/qzxing/tree/master 二、编译与使用 1.下载并解压,解压之后如图所示 2.编译 打开src目录下的QZXing.pro,选择合适的编译器进行编译 最后生…...
MyBatisX插件
MyBatisX插件 MyBatis-Plus为我们提供了强大的mapper和service模板,能够大大的提高开发效率。 但是在真正开发过程中,MyBatis-Plus并不能为我们解决所有问题,例如一些复杂的SQL,多表联查,我们就需要自己去编写代码和SQ…...

《C++20设计模式》学习笔记---原型模式
C20设计模式 第 4 章 原型模式4.1 对象构建4.2 普通拷贝4.3 通过拷贝构造函数进行拷贝4.4 “虚”构造函数4.5 序列化4.6 原型工厂4.7 总结4.8 代码 第 4 章 原型模式 考虑一下我们日常使用的东西,比如汽车或手机。它们并不是从零开始设计的,相反&#x…...

SpringBootAdmin设置邮件通知
如果你想要在Spring Boot Admin中配置邮件通知,可以按照以下步骤进行操作: 添加邮件通知的依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId> </dep…...

深度解析IP应用场景API:提升风险控制与反欺诈能力
前言 在当今数字化时代,网络安全和用户数据保护成为企业日益关注的焦点。IP应用场景API作为一种强大的工具,不仅能够在线调用接口获取IP场景属性,而且具备识别IP真人度的能力,为企业提供了卓越的风险控制和反欺诈业务能力。本文将…...
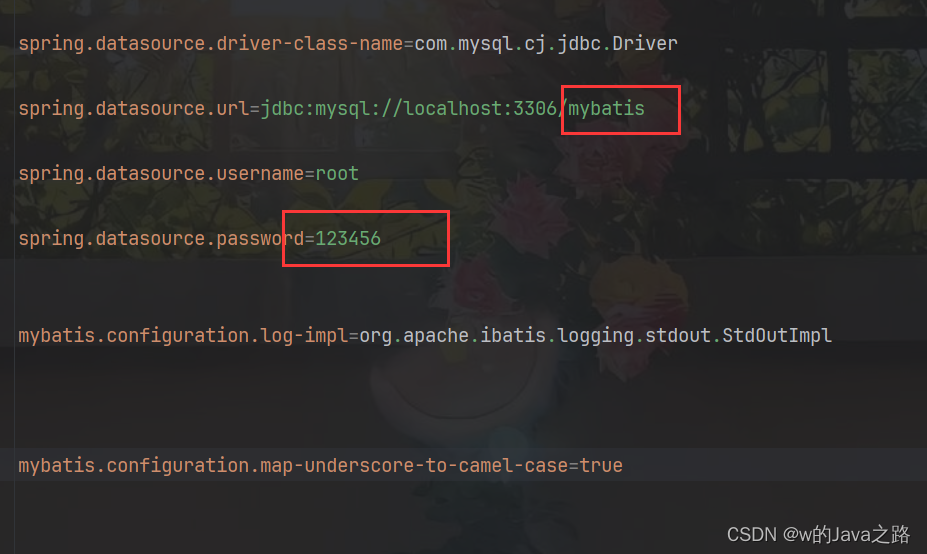
Java连接数据库增删改查-MyBatis
准备工作: 1.创建一个springboot项目,并添加四个依赖 分别是,MyBatis的启动依赖和安装依赖,SQL的依赖,测试依赖,如下: 2.然后创建一张至少两条数据的表 (表可以用各种图形化工具创…...
在国内,现在月薪1万是什么水平?
看到网友发帖问:现在月薪1W是什么水平? 在现如今的情况下,似乎月薪过万这个标准已经成为衡量个人能力的一个标准了,尤其是现在互联网横行的时代,好像年入百万,年入千万就应该是属于大众的平均水平。 我不是…...

【Python网络爬虫入门教程1】成为“Spider Man”的第一课:HTML、Request库、Beautiful Soup库
Python 网络爬虫入门:Spider man的第一课 写在最前面背景知识介绍蛛丝发射器——Request库智能眼镜——Beautiful Soup库 第一课总结 写在最前面 有位粉丝希望学习网络爬虫的实战技巧,想尝试搭建自己的爬虫环境,从网上抓取数据。 前面有写一…...
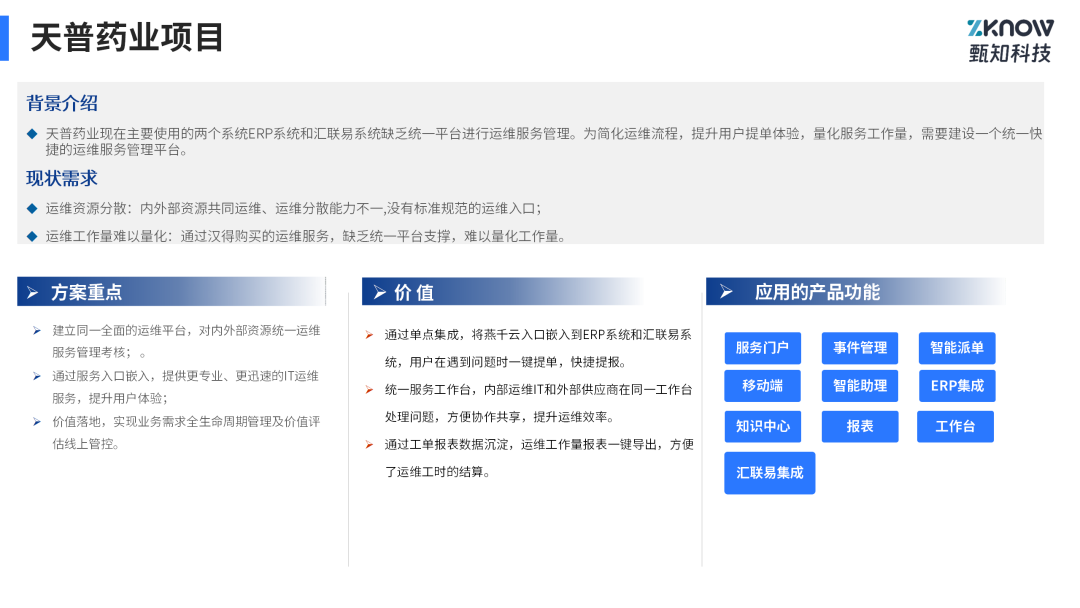
燕千云汇联易联袂出击:护航医企合规,丝滑内外协作
👉 如想详细了解燕千云医药行业快速实施包(ITFA),可继续阅读详细内容: 文/玉娇龙 一. 医药行业数字化挑战 医药研发从基础研究到最终注册上市的整个生命周期长则需要10多年,短则需要6-7年,在漫长…...

【线性代数与矩阵论】Jordan型矩阵
Jordan型矩阵 2023年11月3日 #algebra 文章目录 Jordan型矩阵1. 代数重数与几何重数2. Jordan块与Jordan标准型2.1 最小多项式与Jordan标准型2.2 两类重要矩阵 3. 矩阵的Jordan分解3.1 Jordan分解的应用 下链 1. 代数重数与几何重数 在对向量做线性变换时,向量空间…...

laravel的ORM 对象关系映射
Laravel 中的 ORM(Eloquent ORM)是 Laravel 框架内置的一种对象关系映射系统,用于在 PHP 应用中与数据库进行交互。Eloquent 提供了一种优雅而直观的语法,使得开发者可以使用面向对象的方式进行数据库查询和操作。 定义模型&…...

049:VUE 引入jquery的方法和配置
第049个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下,本专栏提供行之有效的源代码示例和信息点介绍,做到灵活运用。 (1)提供vue2的一些基本操作:安装、引用,模板使…...
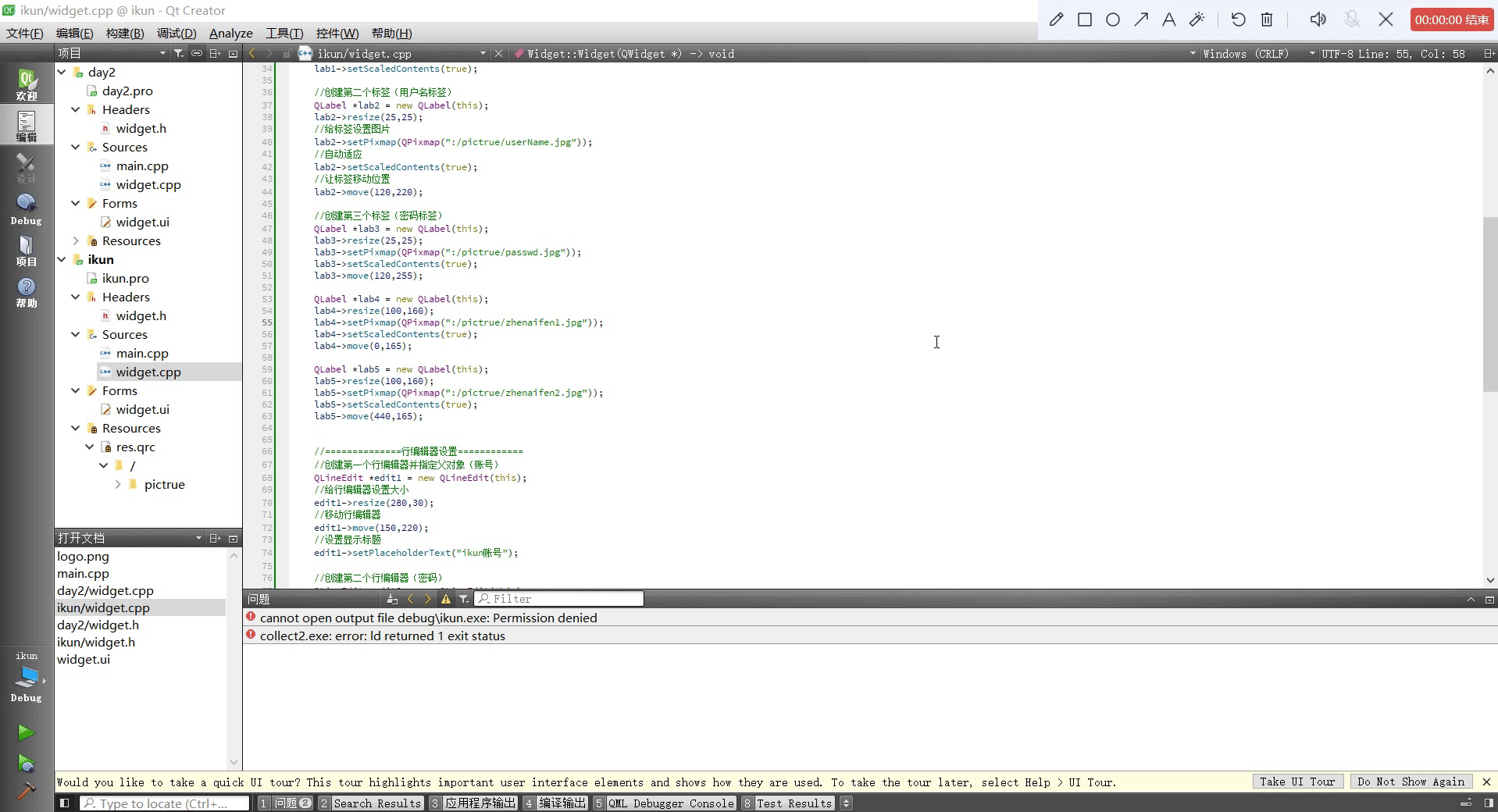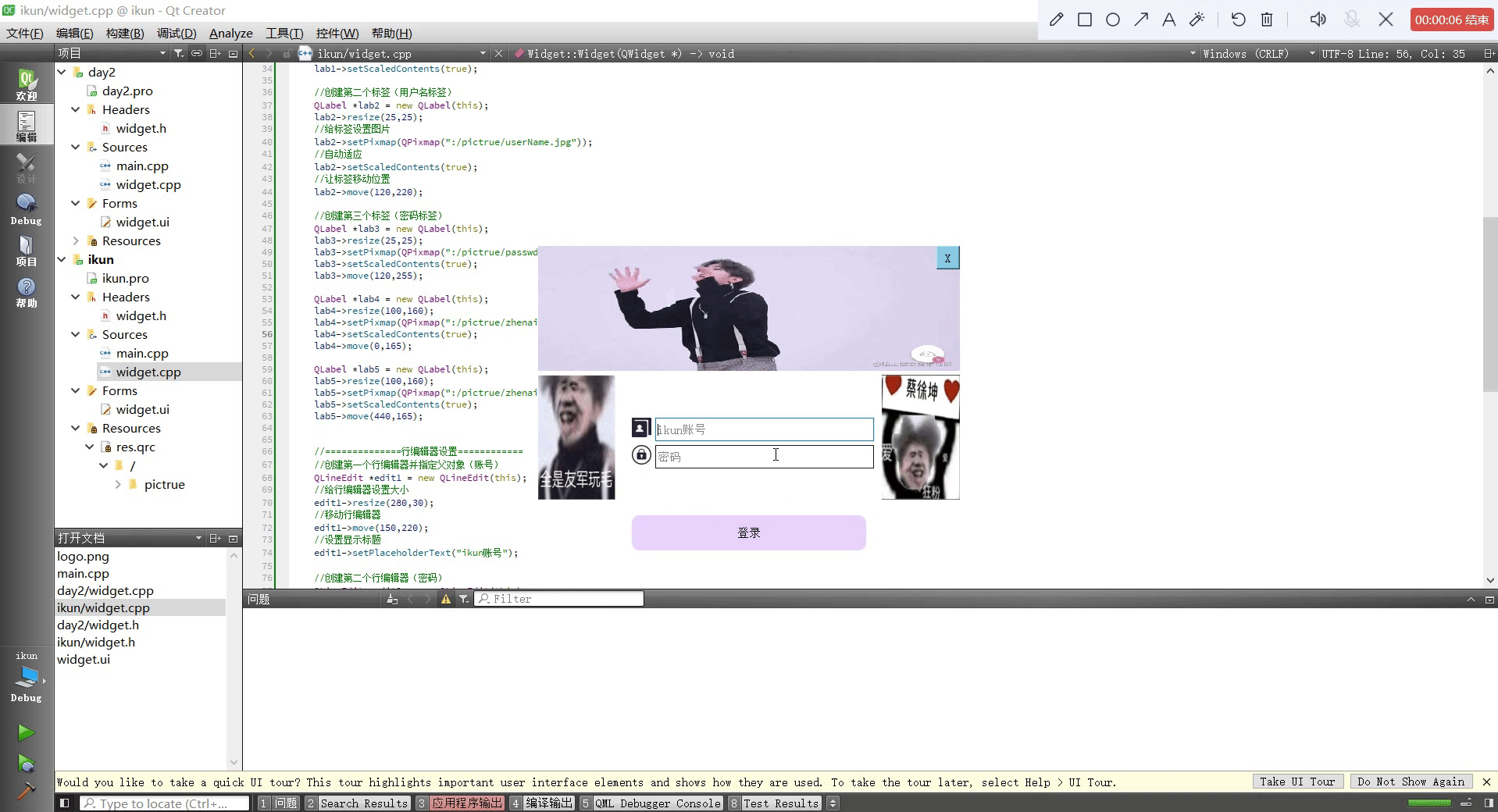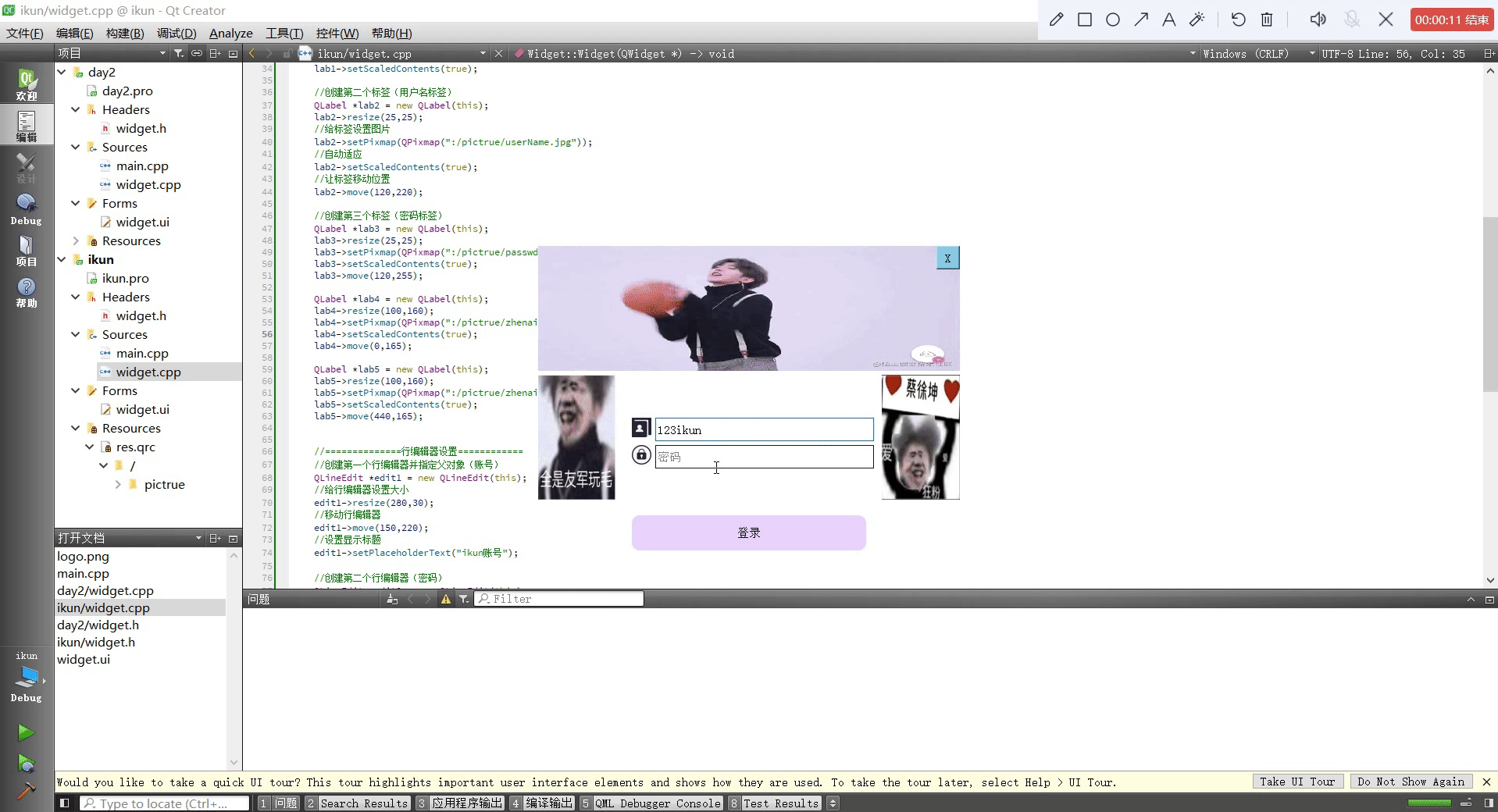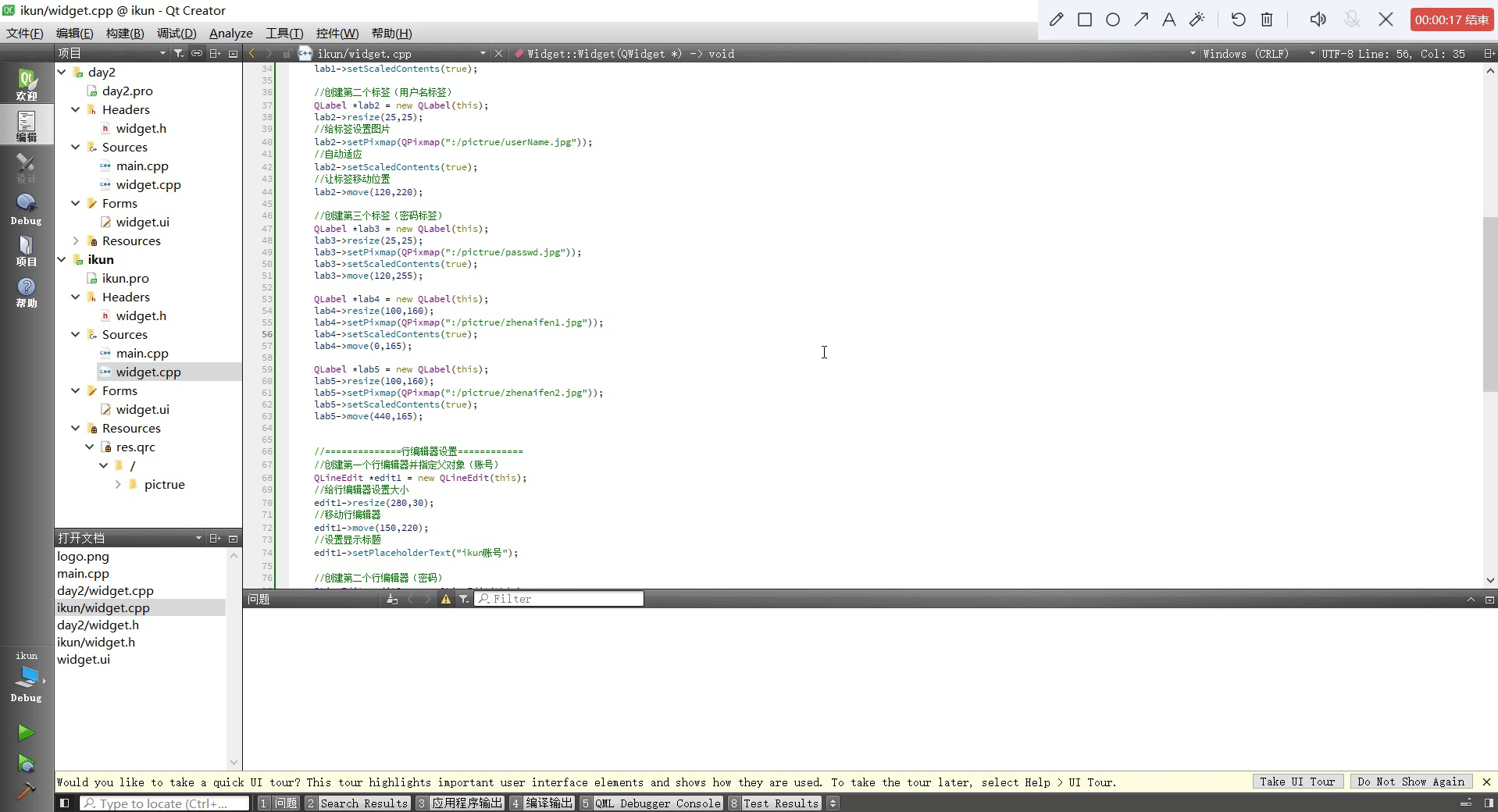
Qt设置类似于qq登录页面
头文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QWindow> #include <QIcon> #include <QLabel> #include <QMovie> #include <QLineEdit> #include <QPushButton>QT_BEGIN_NAMESPACE namespace Ui { class…...
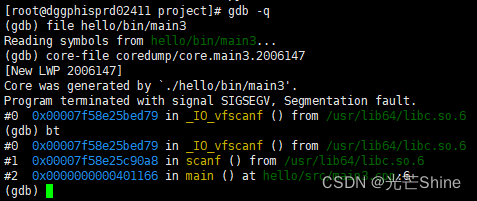
【GDB】
GDB 1. GDB调试器1.1 前言1.2 GDB编译程序1.3 启动GDB1.4 载入被调试程序1.5 查看源码1.6 运行程序1.7 断点设置1.7.1 通过行号设置断点1.7.2 通过函数名设置断点1.7.3 通过条件设置断点1.7.4 查看断点信息1.7.5 删除断点 1.8 单步调试1.9 2. GDB调试core文件2.1 设定core文件的…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
