【数学建模】《实战数学建模:例题与讲解》第九讲-时间序列分析(含Matlab代码)
【数学建模】《实战数学建模:例题与讲解》第九讲-时间序列分析(含Matlab代码)
- 基本概念
- 确定性时间序列分析方法
- 平稳时间序列模型
- ARIMA模型
- 季节性序列
- 习题8.1
- 1. 题目要求
- 2.解题过程
- 3.程序
- 4.结果
- 习题8.2
- 1. 题目要求
- 2.解题过程
- 3.程序
- 4.结果
- 习题8.3
- 1. 题目要求
- 2.解题过程
- 3.程序
- 4.结果
本系列侧重于例题实战与讲解,希望能够在例题中理解相应技巧。文章开头相关基础知识只是进行简单回顾,读者可以搭配课本或其他博客了解相应章节,然后进入本文例题实战,效果更佳。
如果这篇文章对你有帮助,欢迎点赞与收藏~

基本概念
时间序列预测是一种预测方法,它通过将观察对象按照时间顺序排列,构成一个所谓的“时间序列”。通过分析这些时间序列过去的变化规律,可以推断未来的可能变化、趋势和规律。这种方法实际上是一种回归模型,其基本原理有两个方面:一是承认事物发展的延续性,即通过分析过去时间序列的数据来预测事物的发展趋势;二是考虑到偶然因素的影响所带来的随机性。为了减少随机波动的影响,需要利用历史数据进行统计分析,并对数据进行适当处理以进行趋势预测。
时间序列预测法的优点在于其简单易行,易于掌握,能够充分利用原时间序列的数据,计算速度快,并且对模型参数具有动态确定的能力。此外,精度较高,特别是当采用组合时间序列或将时间序列与其他模型组合时,其效果更佳。然而,这种方法也有其局限性,主要是不能反映事物的内在联系,无法分析两个因素之间的相关关系,更适用于短期而非长期预测。
时间序列预测法在各个领域都有广泛的应用,如在金融市场分析、气象预测、工业生产和库存管理等领域。在实际应用中,时间序列预测通常涉及到多种技术和方法,如移动平均、指数平滑法、季节性调整、自回归移动平均模型(ARMA)、自回归积分滑动平均模型(ARIMA)等。这些技术各有特点,适用于不同类型的数据和不同的预测需求。
确定性时间序列分析方法
确定性时间序列分析主要关注那些展现出一定规律或模式的时间序列数据,这些规律通常可以用一组固定的数学函数来描述。这种分析方法试图从时间序列数据中识别出趋势、周期性或季节性等成分。确定性时间序列的主要特点是,一旦识别出其规律,就可以准确预测未来的值。典型的确定性时间序列分析方法包括趋势线分析、季节性分解等。
平稳时间序列模型
平稳时间序列模型是指那些其统计特性(如均值、方差等)随时间推移保持不变的时间序列。在平稳序列中,时间序列的行为不会因时间的改变而发生变化,这使得模型预测变得更加简单和准确。平稳性是很多时间序列模型,如自回归(AR)模型、移动平均(MA)模型、和自回归移动平均(ARMA)模型的重要前提。
ARIMA模型
ARIMA(自回归积分滑动平均)模型是时间序列预测中最常用的方法之一。它结合了自回归(AR)和移动平均(MA)模型,并加入了差分的概念,用以将非平稳时间序列转换为平稳时间序列。ARIMA模型由三个主要参数构成:自回归项(AR)、差分阶数(I,积分)、和移动平均项(MA)。这种模型特别适合处理呈现长期趋势或季节性的非平稳时间序列。
季节性序列
季节性序列指的是那些展现出明显季节性模式的时间序列,即数据在固定时间间隔内呈现出重复模式。这种序列通常与特定季节或周期性事件相关,如月销售量、每日温度变化等。季节性时间序列分析的目的是识别并建模这种周期性模式,以准确预测未来周期内的数值。处理季节性时间序列的常用方法包括季节性分解和季节性ARIMA(SARIMA)模型,后者专门用来处理同时包含季节性和非季节性成分的时间序列。
习题8.1
1. 题目要求


2.解题过程
解:
(1)
由N=3,我们可以取预测公式:
M t + 1 = y t + y t − 1 + y t − 2 3 , t = 3 , 4 , . . . , 11 M_{t+1}=\frac{y_t+y_{t-1}+y_{t-2}}{3},\ t=3,4,...,11 Mt+1=3yt+yt−1+yt−2, t=3,4,...,11
其中 M 9 = 133.0 , M 10 = 136.8 , M 11 = 137.5 M_9=133.0,M_{10}=136.8,M_{11}=137.5 M9=133.0,M10=136.8,M11=137.5 为预测值。
预测的标准误差为:
S = ∑ t = 4 8 ( M t − y t ) 2 5 = 19.3542 S=\sqrt{\frac{\sum_{t=4}^{8}(M_t-y_t)^2}{5}}=19.3542 S=5∑t=48(Mt−yt)2=19.3542
(2)
二次指数平滑法的公式:
{ S t ( 1 ) = α y t + ( 1 − α ) S t − 1 ( 1 ) S t ( 1 ) = α S t ( 1 ) + ( 1 − α ) S t − 1 ( 2 ) \begin{align*} \begin{cases} S_t^{(1)}=\alpha y_t+(1-\alpha)S_{t-1}^{(1)}\\ S_t^{(1)}=\alpha S_t^{(1)}+(1-\alpha)S_{t-1}^{(2)} \end{cases} \end{align*} {St(1)=αyt+(1−α)St−1(1)St(1)=αSt(1)+(1−α)St−1(2)
其中 S t ( 1 ) S_t^{(1)} St(1)为一次指数平滑值, S t ( 2 ) S_t^{(2)} St(2)为二次指数平滑值。
当时间序列开始具有直线趋势时,建立直线指数平滑预测模型:
y ^ t + m = a t + b t m { a t = 2 S t ( 1 ) − S t ( 2 ) b t = α 1 − α ( S t ( 1 ) − S t ( 2 ) ) \begin{align*} &\hat{y}_{t+m}=a_t+b_tm\\ &\begin{cases} a_t=2S_t^{(1)}-S_t^{(2)}\\ b_t=\frac{\alpha}{1-\alpha}(S_t^{(1)}-S_t^{(2)}) \end{cases} \end{align*} y^t+m=at+btm{at=2St(1)−St(2)bt=1−αα(St(1)−St(2))
在 α = 0.3 \alpha=0.3 α=0.3 时,预测的标准误差是:
S = ∑ t = 1 8 ( y ^ t − y t ) 2 7 = 11.7966 S=\sqrt{\frac{\sum_{t=1}^{8}(\hat{y}_t-y_t)^2}{7}} = 11.7966 S=7∑t=18(y^t−yt)2=11.7966
在 α = 0.6 \alpha=0.6 α=0.6 时,预测的标准误差是:
S = ∑ t = 1 8 ( y ^ t − y t ) 2 7 = 7.0136 S=\sqrt{\frac{\sum_{t=1}^{8}(\hat{y}_t-y_t)^2}{7}} = 7.0136 S=7∑t=18(y^t−yt)2=7.0136
(3)
从上面两小问的计算过程来看,选取标准误差最小的,也即 α = 0.6 \alpha=0.6 α=0.6 时的二次指数平滑模型
(4)
按照第三问的结果,取二次指数平滑模型的预测结果即可(计算过程见后文)。
α = 0.6 \alpha=0.6 α=0.6时,1982年的产量预测值为152.9457亿米;1985年的产量预测为182.8640亿米
3.程序
(1)
求解的MATLAB程序如下:
clc, clearyt = [80.8, 94.0, 88.4, 101.5, 110.3, 121.5, 134.7, 142.7];
m = length(yt);
n = 3; % 定义了移动平均窗口的大小
for i = n + 1:m + 1% 在循环内部,用移动平均法计算 ythat 向量的当前元素值,即取窗口内最近的 n 个元素的平均值ythat(i) = sum(yt(i-n:i-1)) / n;
endythatfor i = m + 1:m + nyt(i) = ythat(i);ythat(i+1) = sum(yt(i-n+1:i)) / n;
end% 将 yhat 设置为 ythat 的最后四个元素
yhat = ythat(end-3:end)
% 计算原始数据 yt 和平滑后的数据 ythat 的标准差 s1
% 这里只计算从第 n+1 个元素到最后一个元素的标准差,因为前 n 个元素无法进行平滑处理
% sqrt 和 mean 分别计算标准差的平方和的平均值和标准差本身
s1 = sqrt(mean((yt(n+1:m) - ythat(n+1:m)).^2))
(2)
求解的MATLAB程序如下:(0.3和0.6都尝试一次,仅修改该数据即可)
clc, clearyt = [80.8, 94.0, 88.4, 101.5, 110.3, 121.5, 134.7, 142.7];
n = length(yt);
% 两个平滑值
% 这里使用了简单平均法来计算 st1(1),即前三个数据点的平均值,并将其赋给 st1(1) 和 st2(1)
st1(1) = mean(yt(1:3));
st2(1) = st1(1);
% 平滑系数
alpha = 0.3;% 循环从 i=2 开始,因为 st1(1) 和 st2(1) 已经在前面初始化了
for i = 2:n% 使用指数平滑法更新 st1(i) 和 st2(i)% st1(i) 的更新使用的是单次指数平滑法,而 st2(i) 的更新使用的是二次指数平滑法st1(i) = alpha * yt(i) + (1 - alpha) * st1(i-1);st2(i) = alpha * st1(i) + (1 - alpha) * st2(i-1);
end% 计算趋势系数 at 和 bt
at = 2 * st1 - st2;
bt = alpha / (1 - alpha) * (st1 - st2);
% 计算预测值 yhat
yhat = at + bt;
sigma = sqrt(mean((yt(2:end) - yhat(1:end-1)).^2));
% 根据模型预测最后一个数据点后的趋势,进一步预测接下来四个数据点的值
m = 1:4;
yhat2 = at(end) + bt(end) * m;sigma
yhat2
4.结果
(1)

(2)
在 α = 0.3 \alpha=0.3 α=0.3 时

在 α = 0.6 \alpha=0.6 α=0.6 时

(3)
选取标准误差最小的,也即 α = 0.6 \alpha=0.6 α=0.6 时的二次指数平滑模型
(4)
最终结果:1982年的产量预测值为152.9457亿米;1985年的产量预测为182.8640亿米
习题8.2
1. 题目要求
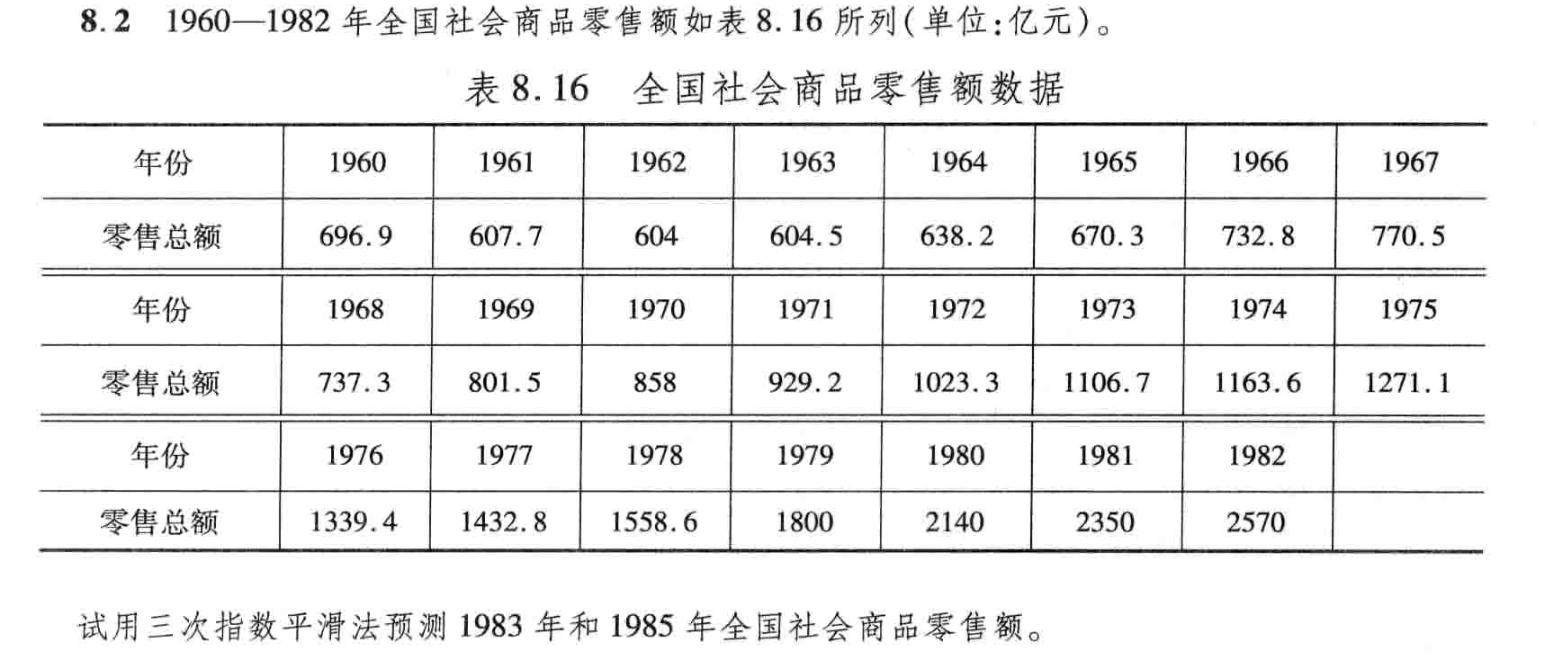
2.解题过程
解:
计算公式为:
{ S t ( 1 ) = α y t + ( 1 − α ) S t − 1 ( 1 ) S t ( 2 ) = α S t ( 1 ) + ( 1 − α ) S t − 1 ( 2 ) S t ( 3 ) = α S t ( 2 ) + ( 1 − α ) S t − 1 ( 3 ) \begin{align*} \begin{cases} S_t^{(1)}=\alpha y_t+(1-\alpha)S_{t-1}^{(1)}\\ S_t^{(2)}=\alpha S_t^{(1)}+(1-\alpha)S_{t-1}^{(2)}\\ S_t^{(3)}=\alpha S_t^{(2)}+(1-\alpha)S_{t-1}^{(3)} \end{cases} \end{align*} ⎩ ⎨ ⎧St(1)=αyt+(1−α)St−1(1)St(2)=αSt(1)+(1−α)St−1(2)St(3)=αSt(2)+(1−α)St−1(3)
其中 S t ( 1 ) , S t ( 2 ) , S t ( 3 ) S_t^{(1)},S_t^{(2)},S_t^{(3)} St(1),St(2),St(3) 分别是一、二、三次指数平滑值。
初始值计算如下:
S 0 ( 1 ) = S 0 ( 2 ) = S 0 ( 3 ) = y 1 + y 2 + y 3 3 = 636.2 S_0^{(1)}=S_0^{(2)}=S_0^{(3)}=\frac{y_1+y_2+y_3}{3}=636.2 S0(1)=S0(2)=S0(3)=3y1+y2+y3=636.2
预测模型为:
y ^ t + m = a t + b t m + c t m 2 , m = 1 , 2 , . . . \hat{y}_{t+m}=a_t+b_tm+c_tm^2,m=1,2,... y^t+m=at+btm+ctm2,m=1,2,...
{ a t = 3 S t ( 1 ) − 3 S t ( 2 ) + S t ( 3 ) b t = α 2 ( 1 − α ) 2 [ ( 6 − 5 α ) S t ( 1 ) − 2 ( 5 − 4 α ) S t ( 2 ) + ( 4 − 3 α ) S t ( 3 ) ] c t = α 2 2 ( 1 − α ) 2 [ S t ( 1 ) − 2 S t ( 2 ) + S t ( 3 ) ] \begin{align*} \begin{cases} a_t=3S_t{(1)}-3S_t{(2)}+S_t{(3)}\\ b_t=\frac{\alpha}{2(1-\alpha)^2}[(6-5\alpha)S_t^{(1)}-2(5-4\alpha)S_t{(2)}+(4-3\alpha)S_t{(3)}]\\ c_t=\frac{\alpha^2}{2(1-\alpha)^2}[S_t^{(1)}-2S_t^{(2)}+S_t^{(3)}] \end{cases} \end{align*} ⎩ ⎨ ⎧at=3St(1)−3St(2)+St(3)bt=2(1−α)2α[(6−5α)St(1)−2(5−4α)St(2)+(4−3α)St(3)]ct=2(1−α)2α2[St(1)−2St(2)+St(3)]
t=23时,计算结果如下:
a 23 = 2572.2613 , b 23 = 259.3374 , c 23 = 8.9819 a_{23}=2572.2613,b_{23}=259.3374,c_{23}=8.9819 a23=2572.2613,b23=259.3374,c23=8.9819
y ^ 23 + m = 8.9819 m 2 + 259.3373 m + 2572.2612 \hat{y}_{23+m}=8.9819m^2+259.3373m+2572.2612 y^23+m=8.9819m2+259.3373m+2572.2612
最终求得:1983、1985年的预测值分别为 2840.58058505076 亿元,3431.11062220508 亿元
3.程序
求解的MATLAB程序如下:
clc, clear% yt记录零售总额数据
yt = [696.9, 607.7, 604, 604.5, 638.2, 670.3, 732.8, 770.5, ...737.3, 801.5, 858, 929.2, 1023.3, 1106.7, 1163.6, 1271.1, ...1339.4, 1432.8, 1558.6, 1800, 2140, 2350, 2570]'; n = length(yt);
alpha = 0.3; % 意味着对于当前时刻的预测,历史数据的权重为 0.7,预测数据的权重为 0.3
st0 = mean(yt(1:3)); % 计算数据向量中前三个数据的平均值,并将其设置为初始平滑值st0% 计算三次指数平滑法中的一阶平滑值st1、二阶平滑值st2和三阶平滑值st3的初始值
st1(1) = alpha * yt(1) + (1 - alpha) * st0;
st2(1) = alpha * st1(1) + (1 - alpha) * st0;
st3(1) = alpha * st2(1) + (1 - alpha) * st0;% 使用循环计算每个时刻的一阶平滑值st1、二阶平滑值st2和三阶平滑值st3
for i = 2:nst1(i) = alpha * yt(i) + (1 - alpha) * st1(i-1);st2(i) = alpha * st1(i) + (1 - alpha) * st2(i-1);st3(i) = alpha * st2(i) + (1 - alpha) * st3(i-1);
end% 根据三次指数平滑法的公式,计算出平滑后的数据yhat、趋势项系数bt和季节项系数ct
at = 3 * st1 - 3 * st2 + st3;
bt = 0.5 * alpha / (1 - alpha)^2 * ...((6 - 5 * alpha) * st1 - 2 * (5 - 4 * alpha) * st2 + (4 - 3 * alpha) * st3);
ct = 0.5 * alpha^2 / (1 - alpha)^2 * ...(st1 - 2 * st2 + st3);
yhat = at + bt + ct;xishu = [ct(end), bt(end), at(end)]
yuce = polyval(xishu, [1:3]) % 计算未来三年的预测值
4.结果
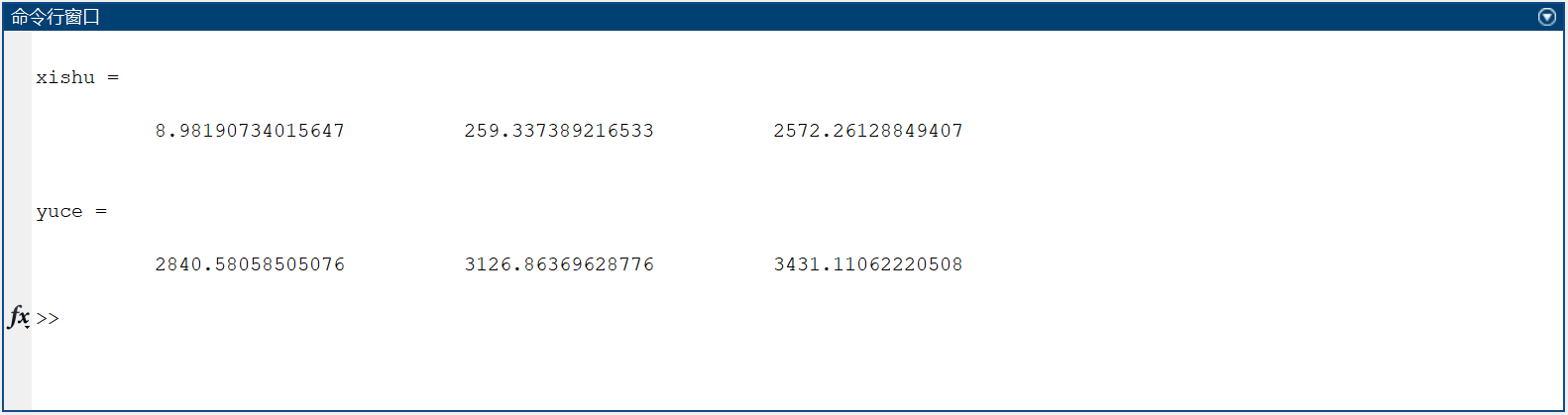
1983、1985年的预测值分别为 2840.58058505076 亿元,3431.11062220508 亿元
习题8.3
1. 题目要求

2.解题过程
解:
本题我选取了两个曲线。
(1)Compertz曲线
一般形式为:
y ^ t = K a b t , K > 0 , 0 < a ≠ 1 , 0 < b ≠ 1 \hat{y}_t=Ka^{b^t},K>0,0<a\neq1,0<b\neq1 y^t=Kabt,K>0,0<a=1,0<b=1
两边取对数
ln y ^ t = ln K + b t ln a \ln\hat{y}_t=\ln K+b^t\ln a lny^t=lnK+btlna
记
y ^ t ′ = ln y ^ , K ′ = ln K , a ′ = ln a \hat{y}'_t = \ln\hat{y},K'=\ln K,a'=\ln a y^t′=lny^,K′=lnK,a′=lna
则
y ^ t ′ = K ′ + a ′ b t \hat{y}'_t=K'+a'b^t y^t′=K′+a′bt
三和法估计参数:
S 1 = ∑ t = 1 m y t ′ , S 1 = ∑ t = m + 1 2 m y t ′ , S 1 = ∑ t = 2 m + 1 3 m y t ′ S_1=\sum_{t=1}^{m}y'_t,S_1=\sum_{t=m+1}^{2m}y'_t,S_1=\sum_{t=2m+1}^{3m}y'_t S1=t=1∑myt′,S1=t=m+1∑2myt′,S1=t=2m+1∑3myt′
则
{ b = ( S 3 − S 2 S 2 − S 1 ) 1 m a ′ = ( S 2 − S 1 ) b − 1 b ( b m − 1 ) 2 K ′ = 1 m [ S 1 − a ′ b ( b m − 1 ) b − 1 ] \begin{align*} \begin{cases} b&=(\frac{S_3-S_2}{S_2-S_1})^{\frac{1}{m}}\\ a'&=(S_2-S_1)\frac{b-1}{b(b^m-1)^2}\\ K'&=\frac{1}{m}[S_1-\frac{a'b(b^m-1)}{b-1}] \end{cases} \end{align*} ⎩ ⎨ ⎧ba′K′=(S2−S1S3−S2)m1=(S2−S1)b(bm−1)2b−1=m1[S1−b−1a′b(bm−1)]
解得
b = 0.8244 , a ′ = − 1.7075 , a = 0.1813 , K ′ = 2.5804 , K = 13.2021 b=0.8244,a'=-1.7075,a=0.1813,K'=2.5804,K=13.2021 b=0.8244,a′=−1.7075,a=0.1813,K′=2.5804,K=13.2021
所以Comperz曲线方程为:
y ^ t = 13.2021 × 0.181 3 0.824 4 t \hat{y}_t=13.2021\times 0.1813^{0.8244^t} y^t=13.2021×0.18130.8244t
1985年,1990年的粮食产量分别为12.3830,12.8840
(2)Logistic曲线
一般形式为:
d y d x = r y ( 1 − y L ) \frac{d y}{d x}=ry(1-\frac{y}{L}) dxdy=ry(1−Ly)
解此微分方程:
y = L 1 + c e − r t y=\frac{L}{1+ce^{-rt}} y=1+ce−rtL
记Logistic曲线一般形式为:
y t = 1 K + a b t , K > 0 , a > 0 , 0 < b ≠ 1 y_t=\frac{1}{K+ab^t},K>0,a>0,0<b\neq1 yt=K+abt1,K>0,a>0,0<b=1
令 y t ′ = 1 y t y'_t=\frac{1}{y_t} yt′=yt1 得:
y t ′ = K + a b t y'_t=K+ab^t yt′=K+abt
三和法估计参数:
S 1 = ∑ t = 1 m y t ′ , S 1 = ∑ t = m + 1 2 m y t ′ , S 1 = ∑ t = 2 m + 1 3 m y t ′ S_1=\sum_{t=1}^{m}y'_t,S_1=\sum_{t=m+1}^{2m}y'_t,S_1=\sum_{t=2m+1}^{3m}y'_t S1=t=1∑myt′,S1=t=m+1∑2myt′,S1=t=2m+1∑3myt′
则
{ b = ( S 3 − S 2 S 2 − S 1 ) 1 m a = ( S 2 − S 1 ) b − 1 b ( b m − 1 ) 2 K = 1 m [ S 1 − a ′ b ( b m − 1 ) b − 1 ] \begin{align*} \begin{cases} b=(\frac{S_3-S_2}{S_2-S_1})^{\frac{1}{m}}\\ a=(S_2-S_1)\frac{b-1}{b(b^m-1)^2}\\ K=\frac{1}{m}[S_1-\frac{a'b(b^m-1)}{b-1}] \end{cases} \end{align*} ⎩ ⎨ ⎧b=(S2−S1S3−S2)m1a=(S2−S1)b(bm−1)2b−1K=m1[S1−b−1a′b(bm−1)]
解得
b = 0.7501 , a = 0.2796 , K = 0.0805 b=0.7501,a=0.2796,K=0.0805 b=0.7501,a=0.2796,K=0.0805
所以Logistic曲线方程为:
y ^ t = 1 0.0805 + 0.2796 × 0.750 1 t \hat{y}_t=\frac{1}{0.0805+0.2796\times0.7501^t} y^t=0.0805+0.2796×0.7501t1
1985年,1990年的粮食产量分别为12.1068,12.3467
3.程序
(1)
求解的MATLAB程序如下:
clc, cleary = [3.78, 4.19, 4.83, 5.46, 6.71, 7.99, 8.60, 9.24, ...9.67, 9.87, 10.49, 10.92, 10.93, 12.39, 12.59];yt = log(y); % 将y取自然对数,以便进行Compertz曲线拟合
n = length(yt);
m = n / 3;
% 计算yt的长度n和m,m是将时间分成三段后的长度
% Compertz曲线需要将时间分成三个等长的部分% 计算yt的前1/3、中间1/3和后1/3的和
s1 = sum(yt(1:m));
s2 = sum(yt(m+1:2*m));
s3 = sum(yt(2*m+1:3*m));b = ((s3 - s2) / (s2 - s1))^(1 / m); % b控制曲线的形状
a = (s2 - s1) * (b - 1) / (b * (b^m - 1)^2); % a控制曲线的位置
k = (s1 - a * b * (b^m - 1) / (b - 1)) / m; % k是拟合曲线的最小值
a = exp(a);
k = exp(k); % 对a和k值进行指数运算,以将其还原为实际值yuce = @(t) k * a.^(b.^t); % 创建一个匿名函数
ypre = yuce([n + 2, n + 7])
(2)
求解的MATLAB程序如下:
clc, cleary = [3.78, 4.19, 4.83, 5.46, 6.71, 7.99, 8.60, 9.24, ...9.67, 9.87, 10.49, 10.92, 10.93, 12.39, 12.59];yt = 1 ./ y;% yt向量的长度n和分成三组时每组的长度m
n = length(yt);
m = n / 3;% 每组的元素之和
s1 = sum(yt(1:m));
s2 = sum(yt(m+1:2*m));
s3 = sum(yt(2*m+1:3*m));% 使用Logistic曲线拟合yt向量。变量b是增长率,变量a是曲线的形状,变量k是曲线的位置
b = ((s3 - s2) / (s2 - s1))^(1 / m);
a = (s2 - s1) * (b - 1) / (b * (b^m - 1)^2);
k = (s1 - a * b * (b^m - 1) / (b - 1)) / m;yuce = @(t) 1 ./ (k + a * b.^t);
ypre = yuce([n + 2, n + 7])
4.结果

如果这篇文章对你有帮助,欢迎点赞与收藏~
相关文章:

【数学建模】《实战数学建模:例题与讲解》第九讲-时间序列分析(含Matlab代码)
【数学建模】《实战数学建模:例题与讲解》第九讲-时间序列分析(含Matlab代码) 基本概念确定性时间序列分析方法平稳时间序列模型ARIMA模型季节性序列 习题8.11. 题目要求2.解题过程3.程序4.结果 习题8.21. 题目要求2.解题过程3.程序4.结果 习…...
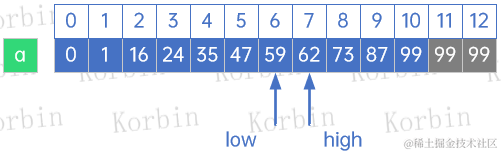
大话数据结构-查找-有序表查找
注:本文同步发布于稀土掘金。 3 有序表查找 3.1 折半查找 折半查找(Binary Search)技术,又称为二分查找,它的前提是线性表中的记录必须是关键码有序(通常从小到大有序),线性表必须…...

Qt实现二维码生成和识别
一、简介 QZxing开源库: 生成和识别条码和二维码 下载地址:https://gitcode.com/mirrors/ftylitak/qzxing/tree/master 二、编译与使用 1.下载并解压,解压之后如图所示 2.编译 打开src目录下的QZXing.pro,选择合适的编译器进行编译 最后生…...
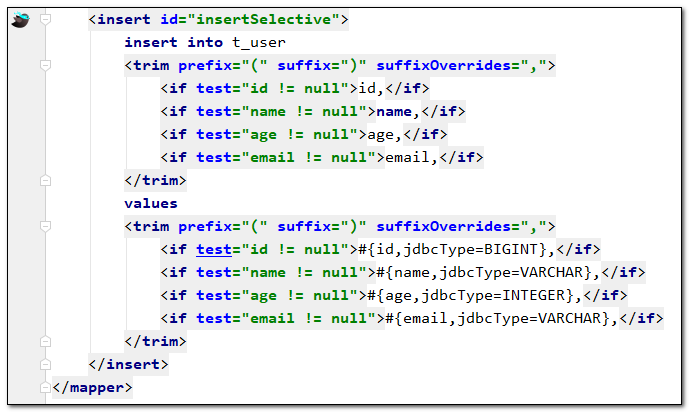
MyBatisX插件
MyBatisX插件 MyBatis-Plus为我们提供了强大的mapper和service模板,能够大大的提高开发效率。 但是在真正开发过程中,MyBatis-Plus并不能为我们解决所有问题,例如一些复杂的SQL,多表联查,我们就需要自己去编写代码和SQ…...

《C++20设计模式》学习笔记---原型模式
C20设计模式 第 4 章 原型模式4.1 对象构建4.2 普通拷贝4.3 通过拷贝构造函数进行拷贝4.4 “虚”构造函数4.5 序列化4.6 原型工厂4.7 总结4.8 代码 第 4 章 原型模式 考虑一下我们日常使用的东西,比如汽车或手机。它们并不是从零开始设计的,相反&#x…...

SpringBootAdmin设置邮件通知
如果你想要在Spring Boot Admin中配置邮件通知,可以按照以下步骤进行操作: 添加邮件通知的依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-mail</artifactId> </dep…...

深度解析IP应用场景API:提升风险控制与反欺诈能力
前言 在当今数字化时代,网络安全和用户数据保护成为企业日益关注的焦点。IP应用场景API作为一种强大的工具,不仅能够在线调用接口获取IP场景属性,而且具备识别IP真人度的能力,为企业提供了卓越的风险控制和反欺诈业务能力。本文将…...
Java连接数据库增删改查-MyBatis
准备工作: 1.创建一个springboot项目,并添加四个依赖 分别是,MyBatis的启动依赖和安装依赖,SQL的依赖,测试依赖,如下: 2.然后创建一张至少两条数据的表 (表可以用各种图形化工具创…...
在国内,现在月薪1万是什么水平?
看到网友发帖问:现在月薪1W是什么水平? 在现如今的情况下,似乎月薪过万这个标准已经成为衡量个人能力的一个标准了,尤其是现在互联网横行的时代,好像年入百万,年入千万就应该是属于大众的平均水平。 我不是…...

【Python网络爬虫入门教程1】成为“Spider Man”的第一课:HTML、Request库、Beautiful Soup库
Python 网络爬虫入门:Spider man的第一课 写在最前面背景知识介绍蛛丝发射器——Request库智能眼镜——Beautiful Soup库 第一课总结 写在最前面 有位粉丝希望学习网络爬虫的实战技巧,想尝试搭建自己的爬虫环境,从网上抓取数据。 前面有写一…...
燕千云汇联易联袂出击:护航医企合规,丝滑内外协作
👉 如想详细了解燕千云医药行业快速实施包(ITFA),可继续阅读详细内容: 文/玉娇龙 一. 医药行业数字化挑战 医药研发从基础研究到最终注册上市的整个生命周期长则需要10多年,短则需要6-7年,在漫长…...

【线性代数与矩阵论】Jordan型矩阵
Jordan型矩阵 2023年11月3日 #algebra 文章目录 Jordan型矩阵1. 代数重数与几何重数2. Jordan块与Jordan标准型2.1 最小多项式与Jordan标准型2.2 两类重要矩阵 3. 矩阵的Jordan分解3.1 Jordan分解的应用 下链 1. 代数重数与几何重数 在对向量做线性变换时,向量空间…...

laravel的ORM 对象关系映射
Laravel 中的 ORM(Eloquent ORM)是 Laravel 框架内置的一种对象关系映射系统,用于在 PHP 应用中与数据库进行交互。Eloquent 提供了一种优雅而直观的语法,使得开发者可以使用面向对象的方式进行数据库查询和操作。 定义模型&…...

049:VUE 引入jquery的方法和配置
第049个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下,本专栏提供行之有效的源代码示例和信息点介绍,做到灵活运用。 (1)提供vue2的一些基本操作:安装、引用,模板使…...
Qt设置类似于qq登录页面
头文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QWindow> #include <QIcon> #include <QLabel> #include <QMovie> #include <QLineEdit> #include <QPushButton>QT_BEGIN_NAMESPACE namespace Ui { class…...
【GDB】
GDB 1. GDB调试器1.1 前言1.2 GDB编译程序1.3 启动GDB1.4 载入被调试程序1.5 查看源码1.6 运行程序1.7 断点设置1.7.1 通过行号设置断点1.7.2 通过函数名设置断点1.7.3 通过条件设置断点1.7.4 查看断点信息1.7.5 删除断点 1.8 单步调试1.9 2. GDB调试core文件2.1 设定core文件的…...

深入了解Java Duration类,对时间的精细操作
阅读建议 嗨,伙计!刷到这篇文章咱们就是有缘人,在阅读这篇文章前我有一些建议: 本篇文章大概6000多字,预计阅读时间长需要5分钟。本篇文章的实战性、理论性较强,是一篇质量分数较高的技术干货文章&#x…...

Python:核心知识点整理大全5-笔记
目录 2. 使用方法pop()删除元素 3. 弹出列表中任何位置处的元素 4. 根据值删除元素 3 章 列表简介 3.3 组织列表 3.3.1 使用方法 sort()对列表进行永久性排序 3.3.2 使用函数 sorted()对列表进行临时排序 3.3.3 倒着打印列表 3.3.4 确定列表的长度 3.5 小结 2. 使用方…...
、微调(fine-tuning)、迁移学习(transfer learning))
预训练(pre-learning)、微调(fine-tuning)、迁移学习(transfer learning)
预训练(pre-learning) 搭建一个网络模型来完成一个特定的图像分类的任务。首先,你需要随机初始化参数,然后开始训练网络,不断调整参数,直到网络的损失越来越小。在训练的过程中,一开始初始化的…...

王道数据结构课后代码题 p149 第8—— 12(c语言代码实现)
目录 8.假设二叉树采用二叉链表存储结构存储,试设计一个算法,计算一棵给定二叉树的所有双分支结点个数。 9.设树B是一棵采用链式结构存储的二叉树,编写一个把树 B中所有结点的左、右子树进行交换的函数。 10.假设二叉树采用二叉链存储结构存储…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
