数组 注意事项
1.一维数组的初始化
int a[5]={1,2,3,4,5}; 合法
int a[5]={1,2,3}; 合法
int a[]={1,2,3,4,5}; 合法,后面决定前面的大小
int a[5]={1,2,3,4,5,6}; 不合法!
2.一维数组的定义
int a[5] 合法
int a[1+1] 合法
int a[1/2+4] 合法
int x=5,a[x] 不合法,x是变量
define P 5 int a[P] 合法
3、二维数组的初始化
int a[2][3]={1,2,3,4,5,6}; 合法,很标准的二维的赋值。
int a[2][3]={1,2,3,4,5}; 合法,后面一个默认为0。
int a[2][3]={{1,2,3},{4,5,6}}; 合法,每行三个。
int a[2][3]={{1,2}{3,4,5}}; 合法,第一行最后一个默认为0。
int a[2][3]={1,2,3,4,5,6,7}; 不合法,赋值的个数多余数组的个数了
int a[][3]={1,2,3,4,5,6}; 合法,可以缺省行的个数。
int a[2][]={1,2,3,4,5,6}; 不合法,不可以缺省列的个数。
定义二维数组时可缺行不缺列;有定义后可缺列不缺行
补充
一维数组的重要概念:
对a[10]这个数组的讨论。
1、a表示数组名,是第一个元素的地址,也就是元素a[0]的地址。(等价于&a)
2、a是地址常量,所以只要出现a++,或者是a=a+2赋值的都是错误的。
3、a是一维数组名,所以它是列指针,也就是说a+1是跳一列。
对a[3][3]的讨论。
1、a表示数组名,是第一个元素的地址,也就是元素a[0][0]的地址。
2、a是地址常量,所以只要出现a++,或者是a=a+2赋值的都是错误的。
3、a是二维数组名,所以它是行指针,也就是说a+1是跳一行。
4、a[0]、a[1]、a[2]也都是地址常量,不可以对它进行赋值操作,同时它们都是列指针,a[0]+1(第0行第二个元素),a[1]+1(第1行第二个元素),a[2]+1(第2行第二个元素)都是跳一列。
5、注意a和a[0](表示二维数组的第0行,即一维数组)、a[1]、a[2]是不同的,它们的基类型是不同的。前者是一行元素,后三者是一列元素。
二维数组做题目的技巧:
如果有a[3][3]={1,2,3, 4,5,6, 7,8,9}这样的题目。
步骤一:把他们写成:第一列 第二列 第三列
a[0] 1 2 3 →第一行
a[1] 4 5 6 →第二行
a[2] 7 8 9 →第三行
步骤二:这样做题目很简单:
*(a[0]+1)我们就知道是第一行的第一个元素往后面跳一列,那么这里就是a[0][1]元素,所以是2。
*(a[1]+2)我们就知道是第二行的第一个元素往后面跳二列。那么这里就是a[1][2]元素,所以是6。
一定记住:只要是二维数组的题目,一定是写成如上的格式,再去做题目,这样会比较简单。
记住以下表达形式:
a[2]变成*(a+2)
a[2][3]变成*(a+2)[3]再可以变成*(*(a+2)+3)
相关文章:

数组 注意事项
1.一维数组的初始化 int a[5]{1,2,3,4,5}; 合法 int a[5]{1,2,3}; 合法 int a[]{1,2,3,4,5}; 合法,后面决定前面的大小 int a[5]{1,2,3,4,5,6}; 不合法! 2.一维数组的定义 int a[5] 合法 int a[11] 合法 int a[1/24] 合法 int x5,a[x…...

day11 滑动窗口中的最大值
class MyQueue { //单调队列(从大到小)public:deque<int> que; // 使用deque来实现单调队列// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。// 同时pop之前判断队列当前是否为空。void…...
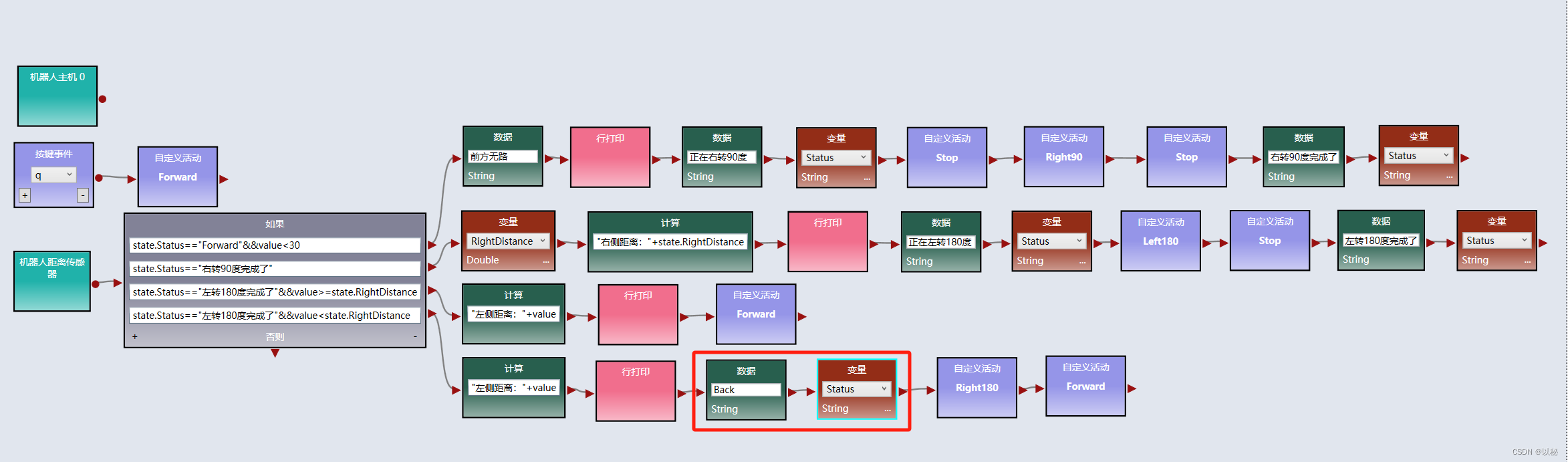
viple模拟器使用(五):Web 2D模拟器中实现两距离局部最优迷宫算法
关于两距离局部最优迷宫算法的原理本文不再赘述,详情请参考:viple模拟器使用(四),归纳总结为: 前方有路,则直行; 前方无路,则右转90度,标记右转完成ÿ…...
)
每日一道算法题 3(2023-12-11)
题目描述: VLAN是一种对局域网设备进行逻辑划分的技术,为了标识不同的VLAN,引入VLAN ID(1-4094之间的整数)的概念。 定义一个VLAN ID的资源池(下称VLAN资源池),资源池中连续的VLAN用开始VLAN-结束VLAN表示,不连续的用单…...
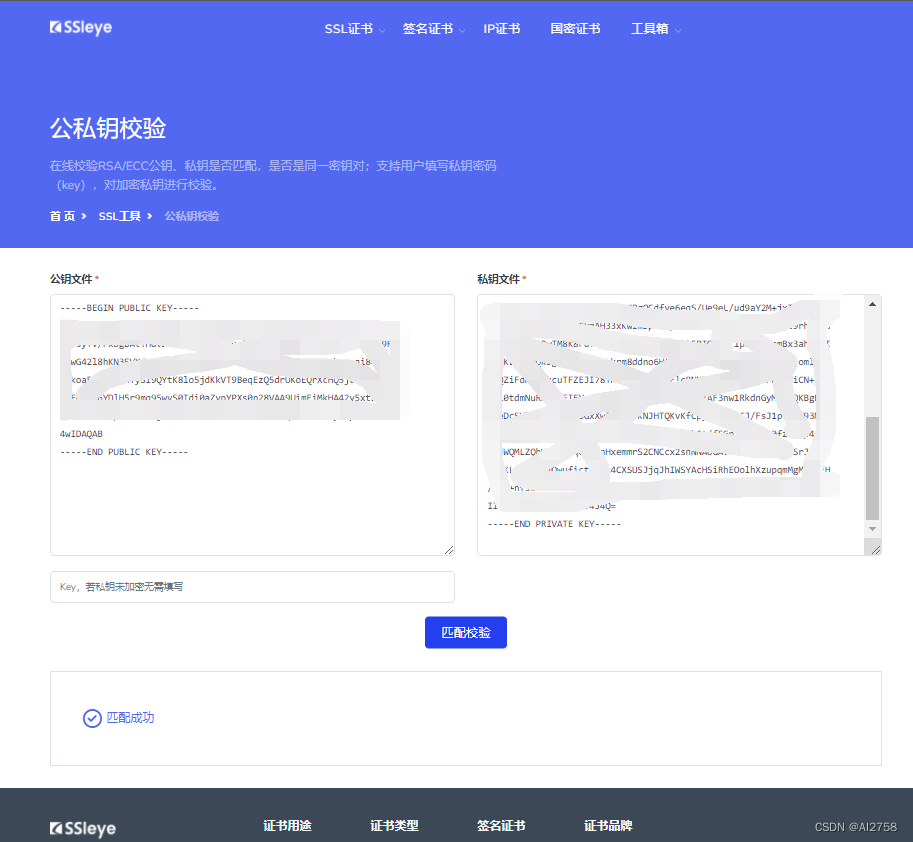
【Android】查看keystore的公钥和私钥
前言: 查看前准备好.keystore文件,安装并配置openssl、keytool。文件路径中不要有中文。 一、查看keystore的公钥: 1.从keystore中获取MD5证书 keytool -list -v -keystore gamekeyold.keystore 2.导出公钥文件 keytool -export -alias …...

ChatGPT的常识
什么是ChatGPT? ChatGPT是一个基于GPT模型的聊天机器人,GPT即“Generative Pre-training Transformer”,是一种预训练的语言模型。ChatGPT使用GPT-2和GPT-3两种模型来生成自然语言响应,从而与人类进行真实的对话。 ChatGPT的设计…...

Spring Boot中的事务是如何实现的?懂吗?
SpringBoot中的事务管理,用得好,能确保数据的一致性和完整性;用得不好,可能会给性能带来不小的影响哦。 基本使用 在SpringBoot中,事务的使用非常简洁。首先,得感谢Spring框架提供的Transactional注解&am…...

应用安全:JAVA反序列化漏洞之殇
应用安全:JAVA反序列化漏洞之殇 概述 序列化是让Java对象脱离Java运行环境的一种手段,可以有效的实现多平台之间的通信、对象持久化存储。Java 序列化是指把 Java 对象转换为字节序列的过程便于保存在内存、文件、数据库中,ObjectOutputStream类的 wri…...
)
基于以太坊的智能合约开发Solidity(函数继承篇)
参考教程:【实战篇】1、函数重载_哔哩哔哩_bilibili 1、函数重载: pragma solidity ^0.5.17;contract overLoadTest {//不带参数function test() public{}//带一个参数function test(address account) public{}//参数类型不同,虽然uint160可…...

【论文极速读】LVM,视觉大模型的GPT时刻?
【论文极速读】LVM,视觉大模型的GPT时刻? FesianXu 20231210 at Baidu Search Team 前言 这一周,LVM在arxiv上刚挂出不久,就被众多自媒体宣传为『视觉大模型的GPT时刻』,笔者抱着强烈的好奇心,在繁忙工作之…...

TS基础语法
前言: 因为在写前端的时候,发现很多UI组件的语法都已经开始使用TS语法,不学习TS根本看不到懂,所以简单的学一下TS语法。为了看UI组件的简单代码,不至于一脸懵。 一、安装node 对于windows来讲,node版本高…...

【基于NLP的微博情感分析:从数据爬取到情感洞察】
基于NLP的微博情感分析:从数据爬取到情感洞察 背景数据集技术选型功能实现创新点 今天我将分享一个基于NLP的微博情感分析项目,通过Python技术、NLP模型和Flask框架,对微博数据进行清洗、分词、可视化,并利用NLP和贝叶斯进行情感分…...

Ubuntu 18.04使用Qemu和GDB搭建运行内核的环境
安装busybox 参考博客: 使用GDBQEMU调试Linux内核环境搭建 一文教你如何使用GDBQemu调试Linux内核 ubuntu22.04搭建qemu环境测试内核 交叉编译busybox 编译busybox出现Library m is needed, can’t exclude it (yet)的解释 S3C2440 制作最新busybox文件系统 https:…...

GEE——利用Landsat系列数据集进行1984-2023EVI指数趋势分析
简介: 利用Landsat系列数据集进行1984-2023EVI指数趋势分析其主要目的是进行长时序的分析,这里我们选用EVI指数,然后进行了4个月的分析,查看其最后的线性趋势以及分布状况。 EVI指数: EVI指数(Enhanced Vegetation Index,增强型植被指数)是一种反映植被生长状态的遥…...
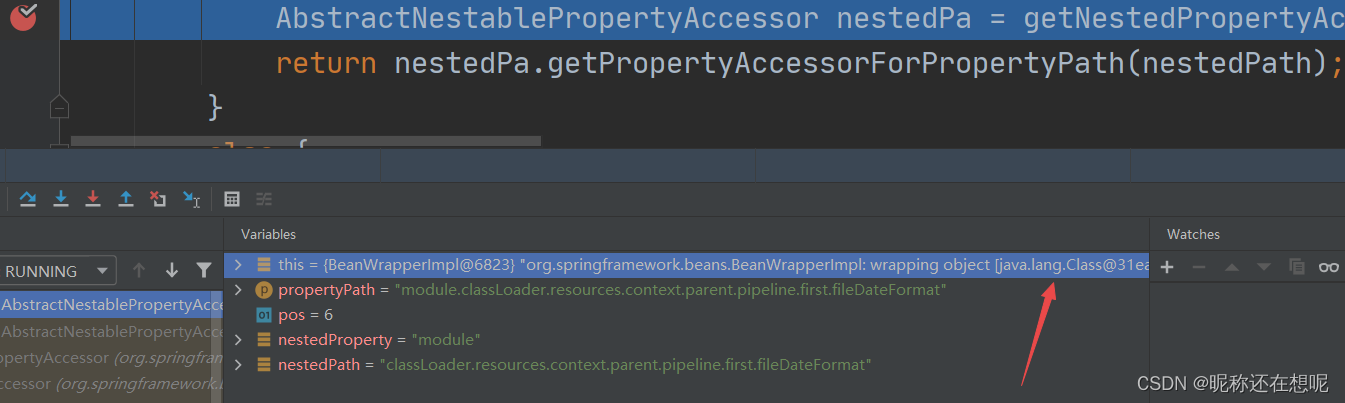
JAVA安全之Spring参数绑定漏洞CVE-2022-22965
前言 在介绍这个漏洞前,介绍下在spring下的参数绑定 在Spring框架中,参数绑定是一种常见的操作,用于将HTTP请求的参数值绑定到Controller方法的参数上。下面是一些示例,展示了如何在Spring中进行参数绑定: 示例1&am…...

辨析旅行商问题(TSP)与车辆路径问题(VRP)
目录 前言旅行商问题 (TSP)问题介绍数学模型符号定义问题输入约束条件目标函数问题输出 解的空间解空间大小计算解释 车辆路径问题 (VRP)问题介绍TSP到VRP的过渡数学模型符号定义问题输入约束条件优化目标问题输出 解空间特殊情况一般情况 TSP 与 VRP 对比 前言 计划是通过本文…...

2024年JAVA招聘行情如何?
大家都在说Java求职不好找,是真的吗?我们来看看数据。 数据支持:根据TIOBE 5月份的编程语言排行榜,Java仍然是前三名之一。这意味着,Java在开发领域仍然占据重要地位。 而在中国的IT市场中,Java仍然是主要…...
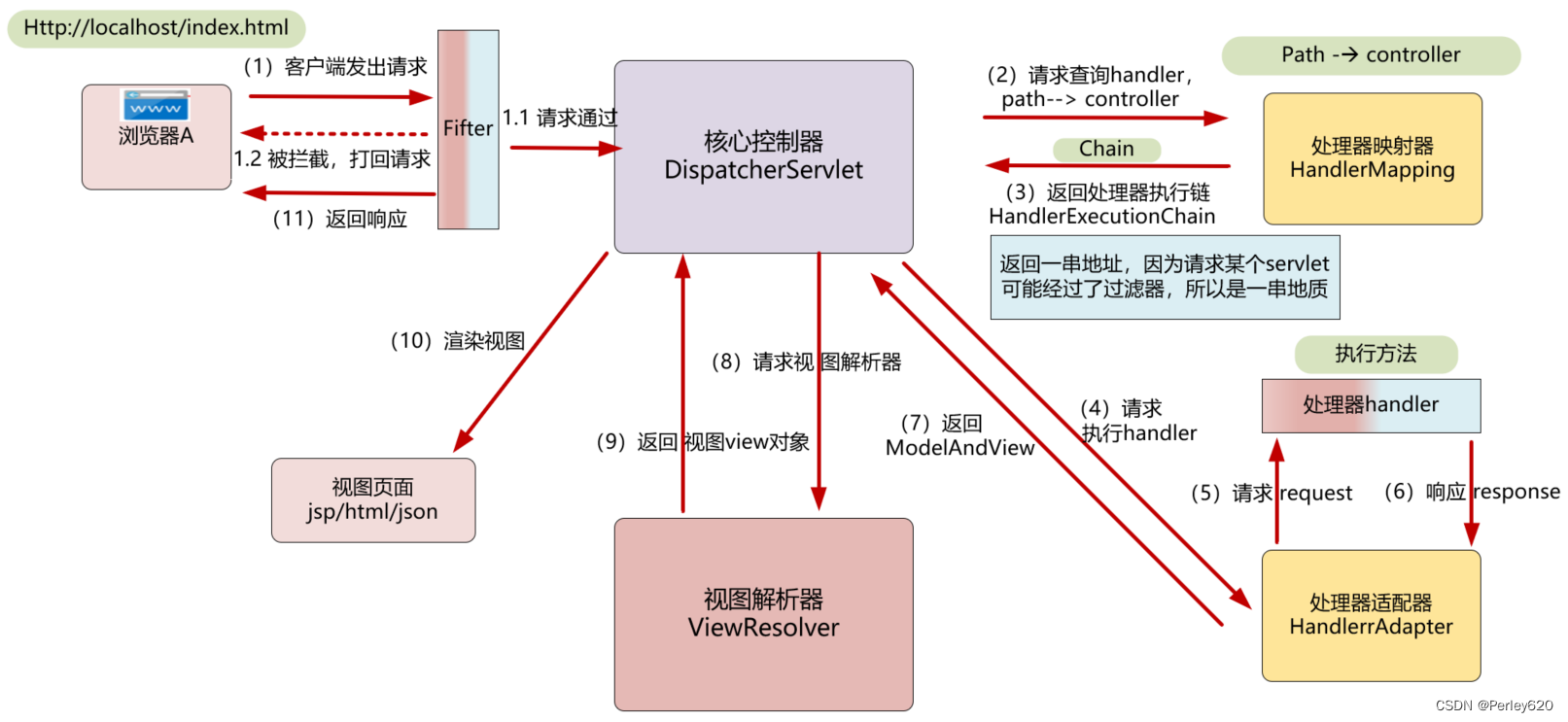
【合集】SpringBoot——Spring,SpringBoot,SpringCloud相关的博客文章合集
前言 本篇博客是spring相关的博客文章合集,内容涵盖Spring,SpringBoot,SpringCloud相关的知识,包括了基础的内容,比如核心容器,springMVC,Data Access;也包括Spring进阶的相关知识&…...

yolov5 获取漏检图片脚本
yolov5 获取漏检图片脚本 获取样本分数在0.05到0.38直接的样本。 # YOLOv5 by Ultralytics, GPL-3.0 licenseimport argparse import json import os import sys import time from pathlib import Pathimport cv2 import numpy as np import torch import torch.backends.cud…...
Unity之OpenXR+XR Interaction Toolkit接入微软VR设备Windows Mixed Reality
前言 Windows Mixed Reality 是 Microsoft 用于增强和虚拟现实体验的VR设备,如下图所示: 在国内,它的使用率很低,一把都是国外使用,所以适配起来是相当费劲。 这台VR设备只能用于串流Windows,启动后,会自动连接Window的Mixed Reality程序,然后打开微软的增强现实门户…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
