【微电网_储能】基于启发式状态机策略和线性程序策略优化方法的微电网中的储能研究【给定系统约束和定价的情况下】(Matlab代码实现)
👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
能源管理系统(EMS)有助于优化微电网中分布式能源(DER)的使用,特别是在涉及可变定价和发电时。本文使用预测定价和负荷条件来优化存储/销售来自电网规模电池系统的能量。演示了两种方法:启发式状态机策略和基于线性程序的优化方法。
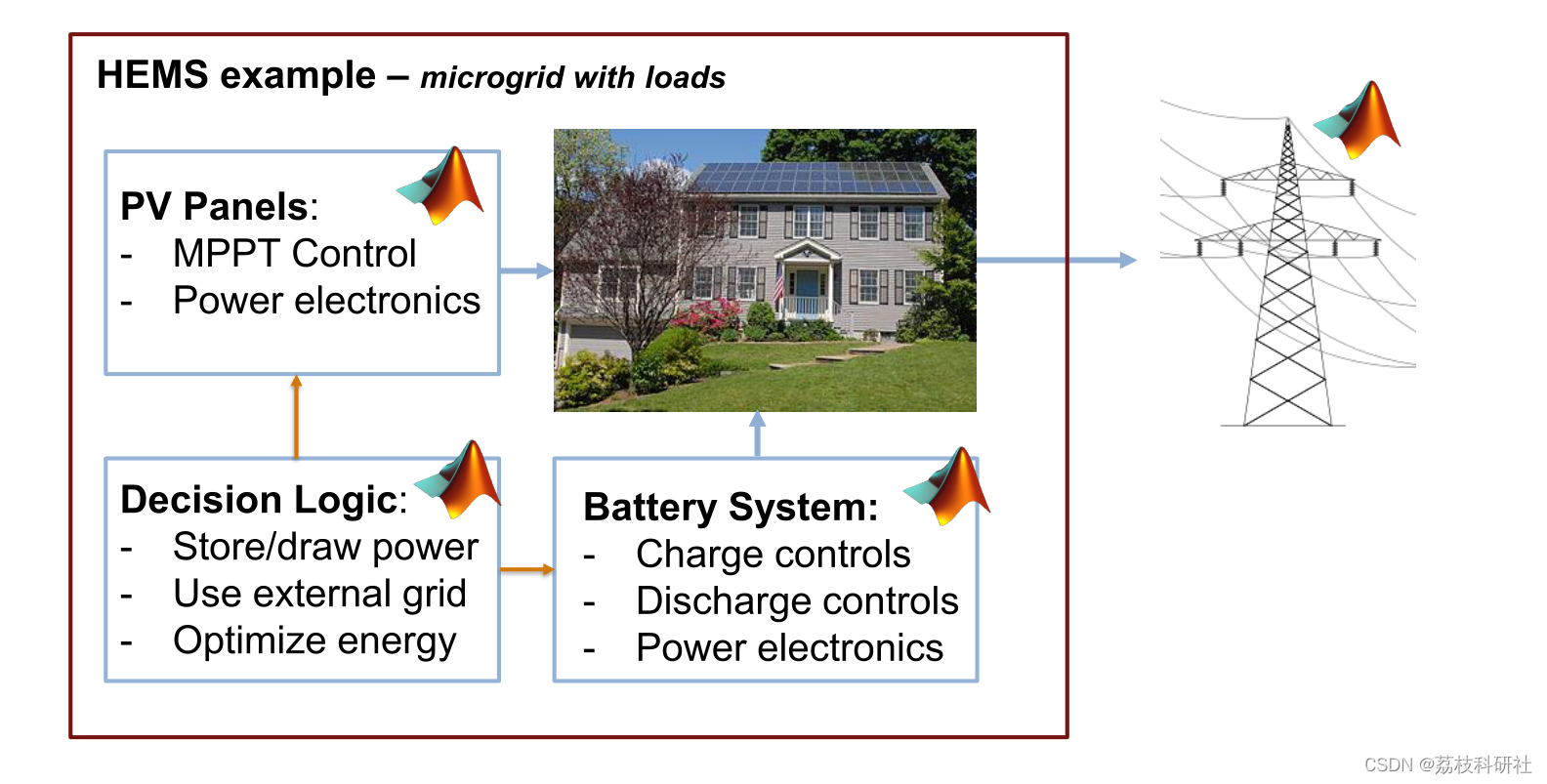







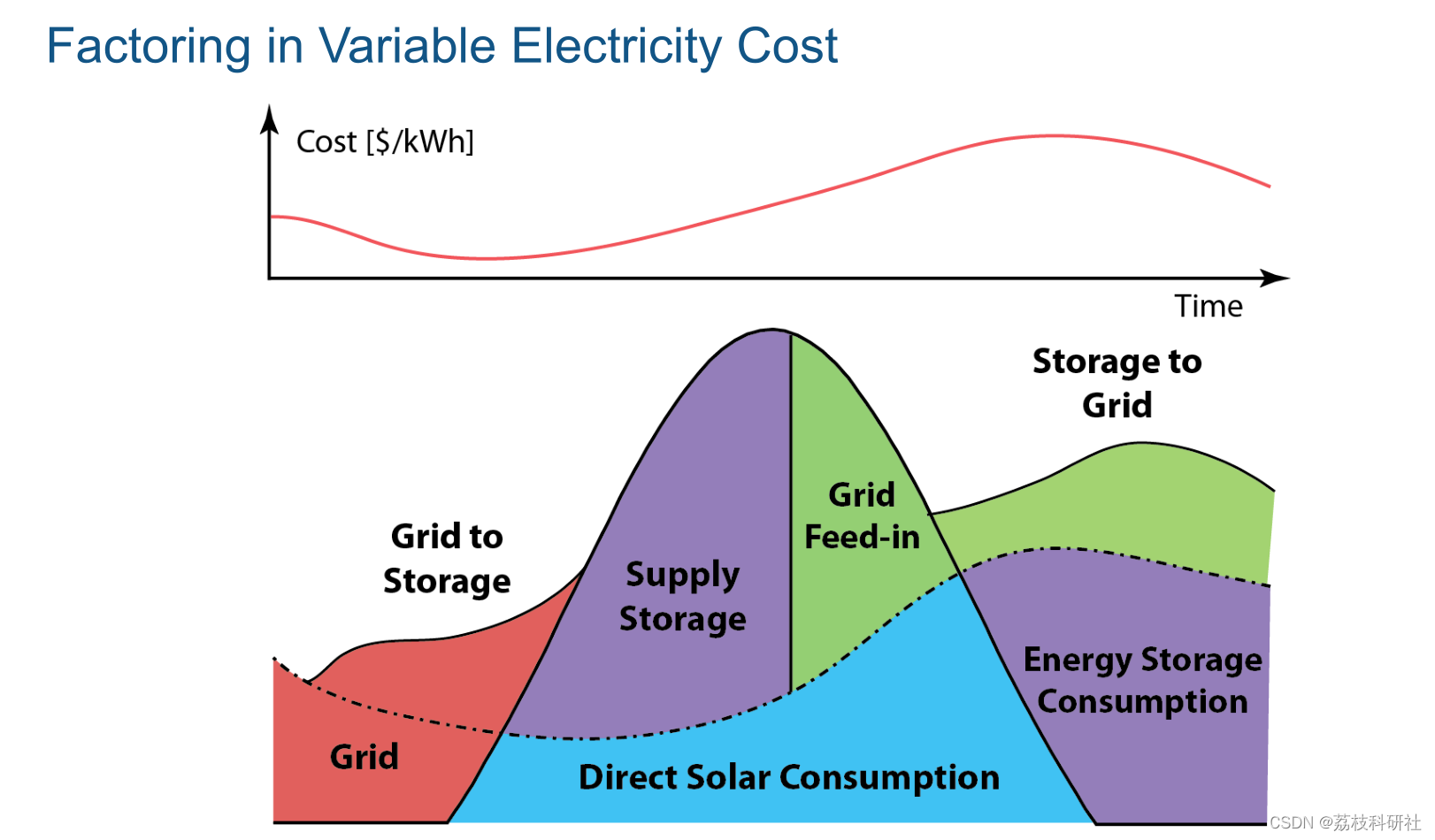







📚2 运行结果
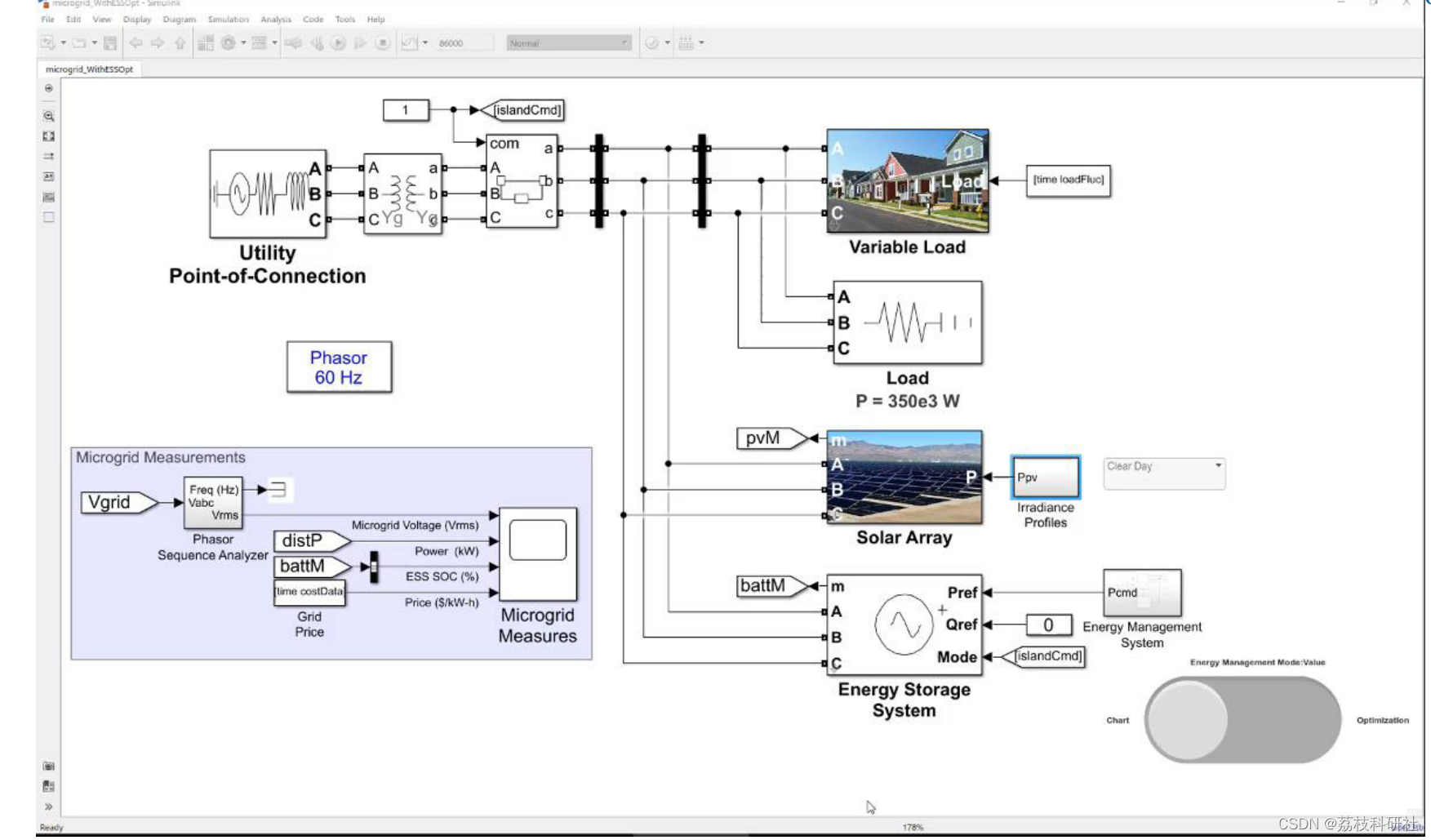





for i = 1:numSimif i <= numOffset*numel(pvDataSet)heuristicCost(end+1) = out(i).logsout{1}.Values.Data(end);elseoptCost(end+1)= out(i).logsout{1}.Values.Data(end);end
end
histogram(heuristicCost); hold on;
histogram(optCost);
legend('Heuristic','Optimization');
xlabel('Cost per Day ($)'); hold off;


部分代码:
function [Pgrid,Pbatt,Ebatt] = battSolarOptimize(N,dt,Ppv,Pload,Einit,Cost,FinalWeight,batteryMinMax)
% Minimize the cost of power from the grid while meeting load with power
% from PV, battery and grid
prob = optimproblem;
% Decision variables
PgridV = optimvar('PgridV',N);
PbattV = optimvar('PbattV',N,'LowerBound',batteryMinMax.Pmin,'UpperBound',batteryMinMax.Pmax);
EbattV = optimvar('EbattV',N,'LowerBound',batteryMinMax.Emin,'UpperBound',batteryMinMax.Emax);
% Minimize cost of electricity from the grid
prob.ObjectiveSense = 'minimize';
prob.Objective = dt*Cost'*PgridV - FinalWeight*EbattV(N);
% Power input/output to battery
prob.Constraints.energyBalance = optimconstr(N);
prob.Constraints.energyBalance(1) = EbattV(1) == Einit;
prob.Constraints.energyBalance(2:N) = EbattV(2:N) == EbattV(1:N-1) - PbattV(1:N-1)*dt;
% Satisfy power load with power from PV, grid and battery
prob.Constraints.loadBalance = Ppv + PgridV + PbattV == Pload;
% Solve the linear program
options = optimoptions(prob.optimoptions,'Display','none');
[values,~,exitflag] = solve(prob,'Options',options);
% Parse optmization results
if exitflag <= 0
Pgrid = zeros(N,1);
Pbatt = zeros(N,1);
Ebatt = zeros(N,1);
else
Pgrid = values.PgridV;
Pbatt = values.PbattV;
Ebatt = values.EbattV;
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Jonathan LeSage (2023). Microgrid Energy Management System (EMS) using Optimization.
🌈4 Matlab代码实现
相关文章:

【微电网_储能】基于启发式状态机策略和线性程序策略优化方法的微电网中的储能研究【给定系统约束和定价的情况下】(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

rk3288-android8-IR-mouse
IR问题: mouse按键使用不了 然后排查: 1.排查上报 ir_key6{ rockchip,usercode <0xbf00>;rockchip,key_table <0xff KEY_POWER>,<0xfe KEY_MUTE>, <0xfd KEY_1>, <0xfc KEY_2>, <0xfb KEY_3>, <0xfa KEY_4>, <0xf9 KEY_5>…...

2023-03-01干活小计
昨天组会,元气大伤,拖更直接。今天继续,三月加油! python魔术方法: __repr__:print()时候调用,注意函数返回值就是打印值。 __len__:len()时候调用 __call__:实例()时候调用 __getitem__:self[i]时候调…...
客户服务软件推荐榜:28款!
在这个竞争激烈的时代,做到服务对企业的存亡有着深刻的意义。改善客户服务,做好客户服务工作,是关键,因为客户服务团队代表着企业的形象,面孔,客户有可能 不大会记得企业的某个东西,但是他们将会…...

Spring注入和注解实现IOC
标题注入依赖注入的方式通过Set方法注入通过构造方法注入自动注入依赖注入的数据类型注入Bean对象注入基本数据类型和字符串注入List注入Set注入Map注入Properties注解实现IOCComponentRepository、Service、Controller注入 依赖注入的方式 在使用依赖注入时,如果…...
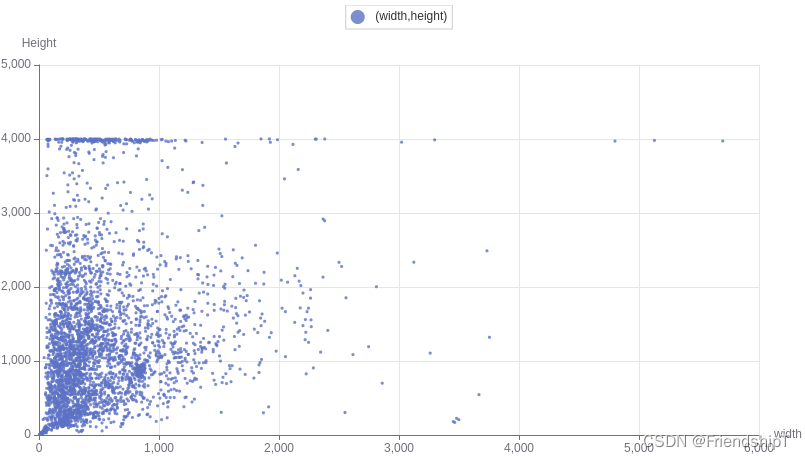
Python统计Labelme标注文件信息并绘制散点图
Python统计Labelme标注文件信息并绘制散点图前言前提条件相关介绍实验环境Python统计Labelme标注文件信息并绘制散点图前言 本文是个人使用Python处理文件的电子笔记,由于水平有限,难免出现错漏,敬请批评改正。更多精彩内容,可点击…...
 客户案例——ET Innovations)
远程接入方案 OpenText Exceed TurboX(ETX) 客户案例——ET Innovations
远程接入方案 OpenText Exceed TurboX(ETX) 客户案例——ET Innovations ET Innovations GmbH 助力奥地利各地的医疗保健专业人员提升患者体验 医疗保健信息系统开发商利用 OpenText™ Exceed™ TurboX 将远程访问其软件的稳定性提高了 95% 公司:ET I…...

Django4.1.7通过djongo1.3.6链接mongoDB6.0.4
网上中文版的djongo链接mongoDB基本都是抄袭州的先生大哥的文章。 文章成文比较久,至少是2019年成文的了,有一些情况发生了变化,今天就自己测试的情况做一些记录。 本文成文日期为:2023年3月2日,请注意参考 废话不多说…...

如何使用FindFunc在IDA Pro中寻找包含指定代码模式的函数代码
关于FindFunc FindFunc是一款功能强大的IDA Pro插件,可以帮助广大研究人员轻松查找包含了特定程序集、代码字节模式、特定命名、字符串或符合其他各种约束条件的代码函数。简而言之,FindFunc的主要目的就是在二进制文件中寻找已知函数。 使用规则过滤 …...
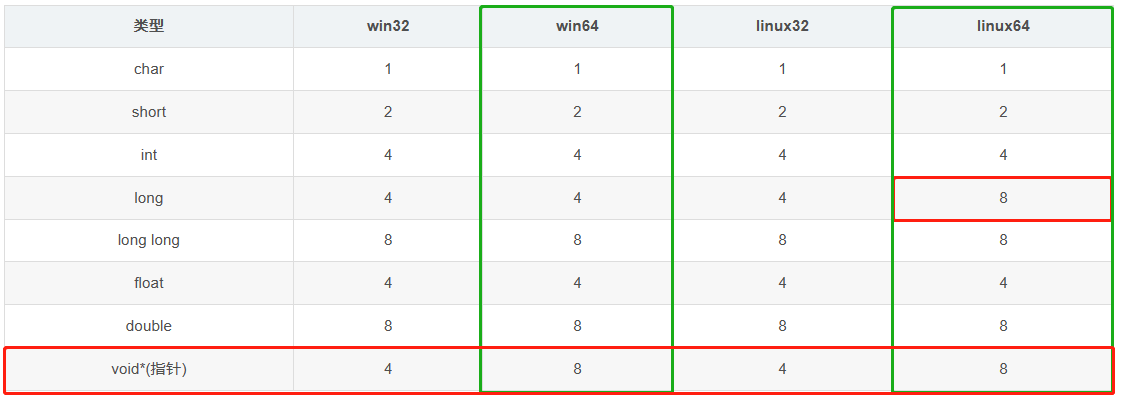
【C++】讲的最通透最易懂的关于结构体内存对齐的问题
目录1. 内存对齐规则2. 简单易懂的内存对齐示例2.1 简单结构体2.2 含位域的结构体2.3 空类的大小2.4 嵌套结构体3. 为什么需要内存对齐?4. 类型在不同系统下所占字节数1. 内存对齐规则 第一个成员在与结构体变量偏移量为0的位置处。其他成员变量要对齐到某个数字&a…...
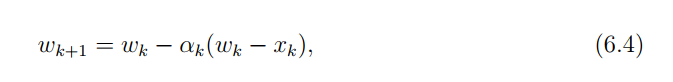
Stochastic Approximation 随机近似方法的详解之(一)
随机近似的定义:它指的是一大类随机迭代算法,用于求根或者优化问题。 Stochastic approximation refers to a broad class of stochastic iterative algorithms solving root finding or optimization problems. temporal-difference algorithms是随机近…...

软件自动化测试工程师面试题集锦
以下是部分面试题目和我的个人回答,回答比较简略,仅供参考。不对之处请指出 1.自我介绍 答:姓名,学历专业,技能,近期工作经历等,可以引导到最擅长的点,比如说代码或者项目 参考&a…...

智合同丨教你做一个懂AI的法律人
作为一名法律人,合同审核工作是日常工作中最基本也是必不可少的一项事务。我们知道,一般在企业,合同审批会涉及到众多部门和职务角色,最关键的一环其实在法务或者律师建议,其他部门给出的审批意见基本上都是基于自己部…...

如何判断自己使用的IP是独享还是共享?
在互联网上,我们常常听到独享IP和共享IP这两个概念。独享IP指的是一个IP地址只被一个用户或一个网站所使用,而共享IP则是多个用户或多个网站共用一个IP地址。那么,如何分辨IP是不是独享呢?接下来,我们将从几个方面来看。在这之前…...

跳石头
题目描述 一年一度的"跳石头"比赛又要开始了! 这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 N 块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳…...
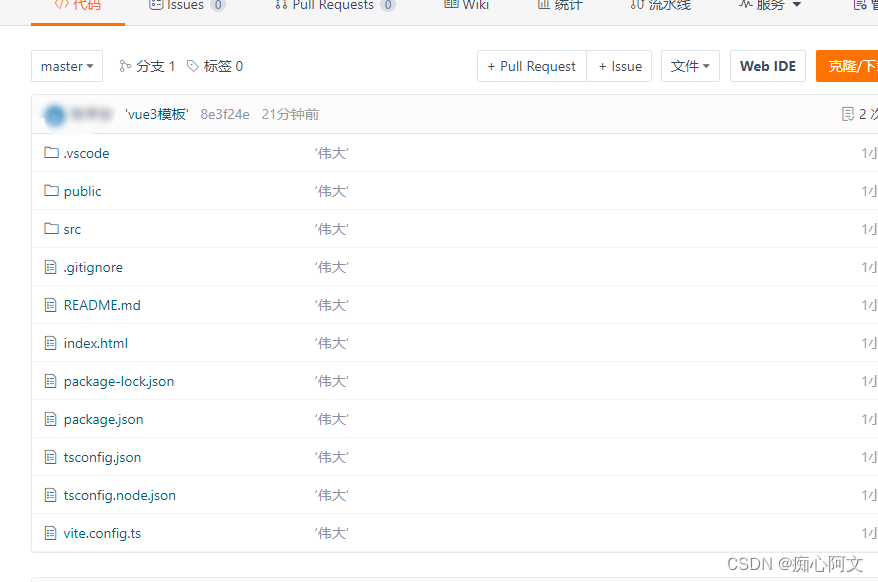
上传gitee教程,Gitee怎么上传代码到仓库
目录 第一步:配置git的用户名和邮箱 第二步:上传到远程仓库 第三步:将仓库的master分支拉取过来和本地的当前分支进行合并 第四步:将修改的所有代码添加到暂存区 第五步:将缓存区内容添加到本地仓库(…...

netstat命令详解
1、下载netstat命令对应的软件包 yum install net-tools -y2、netsta命令介绍 [rootvm01 ~]# man netstatNETSTAT(8) Linux System Administrators Manual NETSTAT(8)NAMEnetstat - Print network connections, routing t…...

数据库三范式
文章目录数据库三范式1. 第一范式(1NF)2. 第二范式(2NF)3. 第三范式(3NF)数据库三范式 第一范式:有主键,具有原子性,字段不可分割第二范式:完全依赖…...

K8S 1.20 弃用 Docker 评估之 Docker 和 OCI 镜像格式的差别
背景 2020 年 12 月初,Kubernetes 在其最新的 Changelog 中宣布,自 Kubernetes 1.20 之后将弃用 Docker 作为容器运行时。 弃用 Docker 带来的,可能是一系列的改变,包括不限于: 容器镜像构建工具容器 CLI容器镜像仓…...

Vue2和Vue3响应式的区别
数据响应式是什么? 所谓 数据响应式 就是建立 响应式数据 与 依赖(调用了响应式数据的操作)之间的关系,当响应式数据发生变化时,可以通知那些使用了这些响应式数据的依赖操作进行相关更新操作,可以是DOM…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
