perf与火焰图-性能分析工具
参考链接
perf性能分析工具使用分享
如何读懂火焰图?-阮一峰
perf基本用法-record,report-知乎
火焰图抓取
准备:
- centos安装perf工具
dnf install perf
- 下载火焰图解析代码
git clone https://github.com/brendangregg/FlameGraph.git
抓取指定进程的火焰图
perf record -F 99 -p xxpid -g -- sleep 60
perf script -i perf.data > perf.unfold
./FlameGraph/stackcollapse-perf.pl perf.unfold > perf.folded
./FlameGraph/flamegraph.pl perf.folded > perf.svg
参数解析
-F 99 :1秒钟进行采集99次
-p xxxid: 采集进程id信息
-a:采集所有cpus信息
-g:收集调用栈
– sleep 30:采集时间为30秒
火焰图说明
y 轴表示调用栈,每一层都是一个函数。调用栈越深,火焰就越高,顶部就是正在执行的函数,下方都是它的父函数。
x 轴表示抽样数,如果一个函数在 x 轴占据的宽度越宽,就表示它被抽到的次数多,即执行的时间长。注意,x 轴不代表时间,而是所有的调用栈合并后,按字母顺序排列的。
火焰图就是看顶层的哪个函数占据的宽度最大。只要有"平顶"(plateaus),就表示该函数可能存在性能问题。
注意:
./FlameGraph/stackcollapse-perf.pl和./FlameGraph/flamegraph.pl 为FlameGraph.git中的工具,负责火焰图数据的解析,需要注意可执行权限。
相关文章:

perf与火焰图-性能分析工具
参考链接 perf性能分析工具使用分享 如何读懂火焰图?-阮一峰 perf基本用法-record,report-知乎 火焰图抓取 准备: centos安装perf工具 dnf install perf下载火焰图解析代码 git clone https://github.com/brendangregg/FlameGraph.git抓取指定进程…...
UniGui使用CSSUniTreeMenu滚动条
有些人反应UniTreeMenu当菜单项目比较多的时候会超出但是没有出滚动条,只需要添加如下CSS 老规矩,unitreemeu的layout的componentcls里添加bbtreemenu,然后在css里添加 .bbtreemenu .x-box-item{ overflow-y: auto; } 然后当内容超出后就会…...

Spring框架中的五种常用设计模式
1、单例模式 Spring 的 Bean 默认是单例模式,通过 Spring 容器管理 Bean 的⽣命周期,保证每个 Bean 只被 创建⼀次,并在整个应⽤程序中重用。 2.工厂模式 Spring 使⽤⼯⼚模式通过 BeanFactory 和 ApplicationContext 创建并管理 Bean 对象…...

华纳云:docker启动报错的原因和解决方法
Docker 启动报错可能由多种原因引起。以下是一些建议,可用于解决 Docker 启动问题: 查看 Docker 日志: 查看 Docker 的日志可以提供更多的详细信息,有助于定位问题。 sudo journalctl -xe | grep docker 或者查看 Docker 服务的详…...

代码规范及开发工具
代码规范及开发工具: 前端(vscode、idea): JavaScript规范: 1. 谷歌开源项目风格指南:JavaScript 、TypeScript篇 https://zh-google-styleguide.readthedocs.io/en/latest/google-typescript-…...
证件照制作小程序源代码
17638103951(同v)...

自治调优!人大金仓解放DBA双手
数据库系统的性能是确保整个应用系统高效运转的关键因素,因此数据库性能调优工作至关重要。KingbaseES通过将人工调优过程内化为数据库内核,成功实现了自治调优。这种创新的调优方案为DBA提供了更高效且准确的性能调优途径,同时也显著降低了数…...
深度学习环境配置------windows系统(GPU)------Pytorch
深度学习环境配置------windows系统(GPU)------Pytorch 准备工作明确操作系统明确显卡系列 CUDA和Cudnn下载与安装1.下载2.安装 环境配置过程1.安装Anacoda2.配置环境1)创建一个新的虚拟环境2)pytorch相关库的安装 2.安装VScode1&…...
el-menu标题过长显示不全问题处理
项目基于vue-element-admin 问题 期望 处理方式 \src\layout\components\Sidebar\index.vue 文件后添加CSS <style scped> /* 侧栏导航菜单经典 文字超长溢出问题 CSS折行 */ .el-submenu__title {display: flex;align-items: center; } .el-submenu__title span {white-…...

微信游戏开发:连接社交与娱乐的创新之路
在移动互联网时代,微信已经成为了人们日常生活中不可或缺的社交工具。而微信游戏,作为在这一平台上崛起的新兴产业,不仅给用户提供了更多娱乐选择,也为开发者们创造了独特的机遇。本文将探讨微信游戏开发的关键步骤、技术要点以及…...

1688一件采购实现指南:含代码实现采购流程
一、引言 1688是中国最大的B2B电子商务平台之一,提供了丰富的商品信息和采购服务。一键采购是1688平台的一项便捷功能,可以帮助用户快速完成采购流程,提高采购效率。本文将详细介绍如何使用1688一键采购功能,并通过代码示例演示如…...
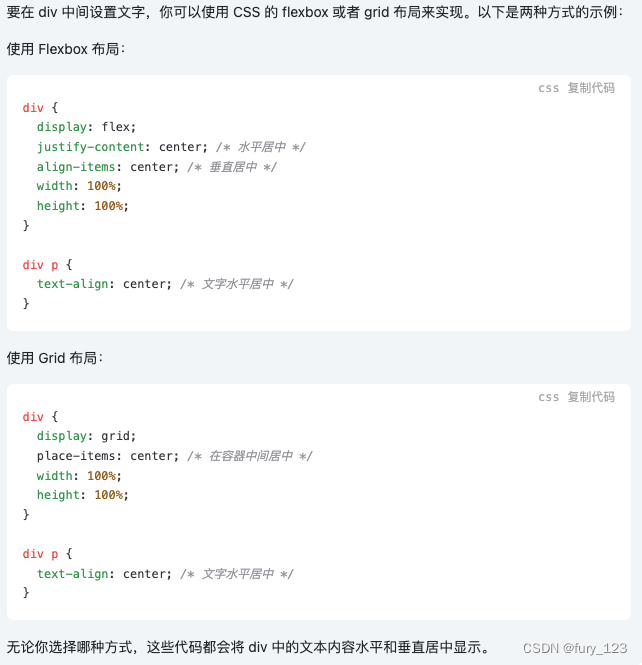
div中一个图片怎么铺满整个div而且不超出div按比例铺满div
重要信息: background-size:cover或者background-size:contain;属性 设置图片不重复: background-repeat:no-repeat; 设置字体在div中间:...
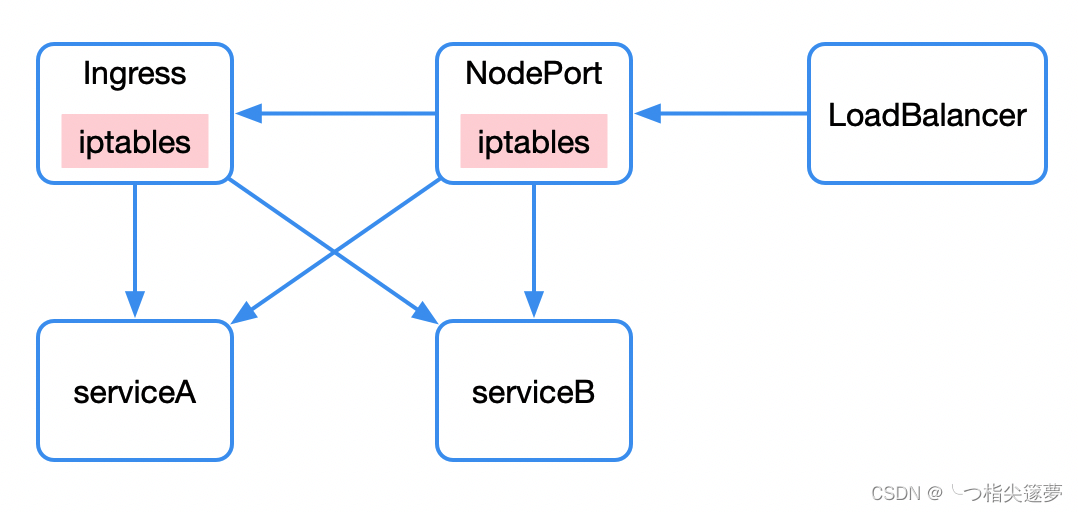
云原生之深入解析Kubernetes的架构及特性
一、kubernetes 架构 从宏观上来看 kubernetes 的整体架构,包括 Master、Node 以及 Etcd。Master 即主节点,负责控制整个 kubernetes 集群,它包括 Api Server、Scheduler、Controller 等组成部分。它们都需要和 Etcd 进行交互以存储数据&…...

分布工具类的定义与实现及测试。
package d5.util;public class PageUtil {private int pageSize;//一页有多少条private int currIndex;//当前是第几页private int totalCount;//共有多少条记录 谁给我? 逻辑层的 getTotalCountprivate int totalPage;//共有多少页 private int start;//显时时开始…...

如何在忘记密码的情况下恢复解锁 iPhone
您忘记了 iPhone 密码吗?Apple 官方通常建议将 iPhone 恢复至出厂设置以将其删除。这种修复很不方便,甚至可能比问题本身更麻烦。 如果您也经历过同样的情况,并且想知道忘记了 iPhone 密码并且不想恢复它该怎么办,我们的终极指南…...

通过compileall库将python文件编译为pyc文件
文章目录 什么是 .pyc 文件将 .py 文件编译为 .pyc 文件编译单个文件编译多个文件 在实际开发中,有时候需要将产品(以.py文件为例)发布到外部环境,但我们并不想显式地让别人看到我们的源码,此时就需要对源码进行加密保…...
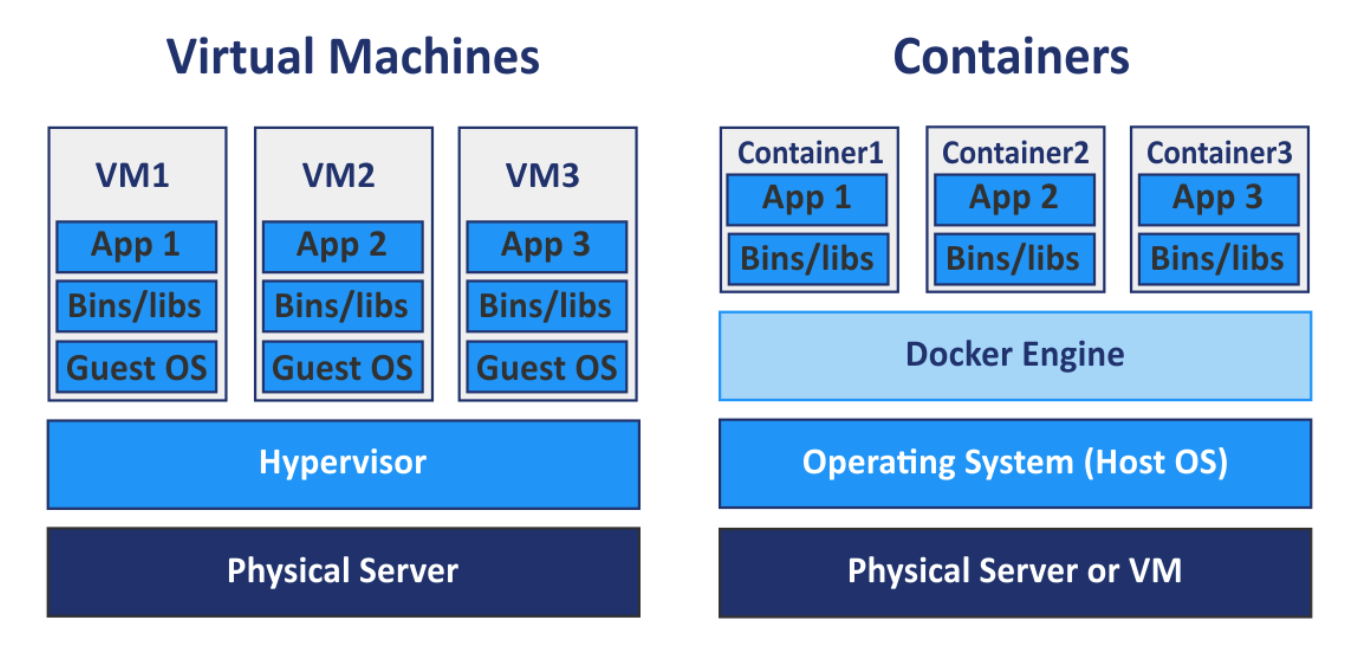
【Docker】深入理解Docker:一种革新性的容器技术
前言 Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的容器中,然后发布到任何流行的Linux或Windows操作系统的机器上,也可以实现虚拟化,容器是完全使用沙箱机制,相互之间不会有任何接口。 📕作者简介:热…...

数据库——安全性
智能2112杨阳 一、目的与要求: 1、设计用户子模式 2、根据实际需要创建用户角色及用户,并授权 3、针对不同级别的用户定义不同的视图,以保证系统的安全性 二、内容: 先创建四类用户角色: 管理员角色Cusm、客户角…...

Vue路由跳转重定向动态路由VueCli
Vue路由跳转&重定向&动态路由&VueCli 一、声明式导航-导航链接 1.需求 实现导航高亮效果 如果使用a标签进行跳转的话,需要给当前跳转的导航加样式,同时要移除上一个a标签的样式,太麻烦!!! …...

mysql 当前时间加3个工作日
1. 问题描述: 在日常工作中可能会遇到计算工作日的情况 2. 解决过程 (1) 首先制作一个假日表 holiday_config CREATE TABLE holiday_config (id int(10) NOT NULL AUTO_INCREMENT,holiday varchar(8) DEFAULT NULL,PRIMARY KEY (id) USING BTREE ) ENGINEInnoDB…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
