2023-12-14 二叉树的最大深度和二叉树的最小深度以及完全二叉树的节点个数
二叉树的最大深度和二叉树的最小深度以及完全二叉树的节点个数
104. 二叉树的最大深度
思想:可以使用迭代法或者递归!使用递归更好,帮助理解递归思路!明确递归三部曲–①确定参数以及返回参数 ②递归结束条件 ③单层逻辑是怎么样的!
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:# 确定递归的参数以及返回# 什么时候结束递归# 递归的单层逻辑是怎么样的def dp(node):if not node:return 0left_length = dp(node.left)right_length = dp(node.right)return 1 + max(left_length, right_length)return dp(root)111. 二叉树的最小深度
思想:看似和最大深度相似,实则不同的!还需要考虑一个节点为None但是另一个不为None的情况!这个是关键!如果是参加面试最好使用迭代法来做,也就是广度优先遍历这样会更快更好理解【判断节点是否有左右节点即可】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def minDepth(self, root: Optional[TreeNode]) -> int:# 使用递归的方法--参数为TreeNode 返回int;结束条件左右节点皆为None;单层逻辑;def deth_dp(node):if not node:return 0left_length = deth_dp(node.left)right_length = deth_dp(node.right)# 还需要判断目前是否已经是叶子节点了if not node.left and node.right:return 1 + right_lengthelif node.left and not node.right:return 1 + left_length# 最后都为None 直接比较返回就好了return 1 + min(left_length, right_length)return deth_dp(root)
222. 完全二叉树的节点个数
思想:和最大深度很像,返回值等于左右节点相加即可!
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def countNodes(self, root: Optional[TreeNode]) -> int:def add_deth(node):if not node:return 0left_length = add_deth(node.left)right_length = add_deth(node.right)return 1 + left_length + right_lengthreturn add_deth(root)
相关文章:

2023-12-14 二叉树的最大深度和二叉树的最小深度以及完全二叉树的节点个数
二叉树的最大深度和二叉树的最小深度以及完全二叉树的节点个数 104. 二叉树的最大深度 思想:可以使用迭代法或者递归!使用递归更好,帮助理解递归思路!明确递归三部曲–①确定参数以及返回参数 ②递归结束条件 ③单层逻辑是怎么样…...
利用闭包与高阶函数实现缓存函数的创建
缓存函数是一种用于存储和重复利用计算结果的机制。其基本思想是,当一个函数被调用并计算出结果时,将该结果存储在某种数据结构中 (通常是一个缓存对象)以备将来使用。当相同的输入参数再次传递给函数时,不再执行实际的计算,而是直…...

P1042 [NOIP2003 普及组] 乒乓球 JAVA 题解
题目背景 国际乒联现在主席沙拉拉自从上任以来就立志于推行一系列改革,以推动乒乓球运动在全球的普及。其中11分制改革引起了很大的争议,有一部分球员因为无法适应新规则只能选择退役。华华就是其中一位,他退役之后走上了乒乓球研究工作&…...

最大公因数,最小公倍数详解
前言 对于初学编程的小伙伴们肯定经常遇见此类问题,而且为之头疼,今天我来给大家分享一下,最大公因数和最小公倍数的求法。让我们开始吧! 文章目录 1,最大公因数法1法2法3 2,最小公倍数3,尾声 …...
无脑利用API实现文心一言AI对话功能?(附代码)
前言:在当今数字化的时代,人工智能(AI)技术正在不断演进,为开发者提供了丰富的工具和资源。其中,API(应用程序接口)成为构建强大AI应用的关键组成部分之一。本文将介绍如何利用API来…...

加速数据采集:用OkHttp和Kotlin构建Amazon图片爬虫
引言 曾想过轻松获取亚马逊上的商品图片用于项目或研究吗?是否曾面对网络速度慢或被网站反爬虫机制拦截而无法完成数据采集任务?如果是,那么本文将为您介绍如何用OkHttp和Kotlin构建一个高效的Amazon图片爬虫解决方案。 背景介绍 亚马逊&a…...
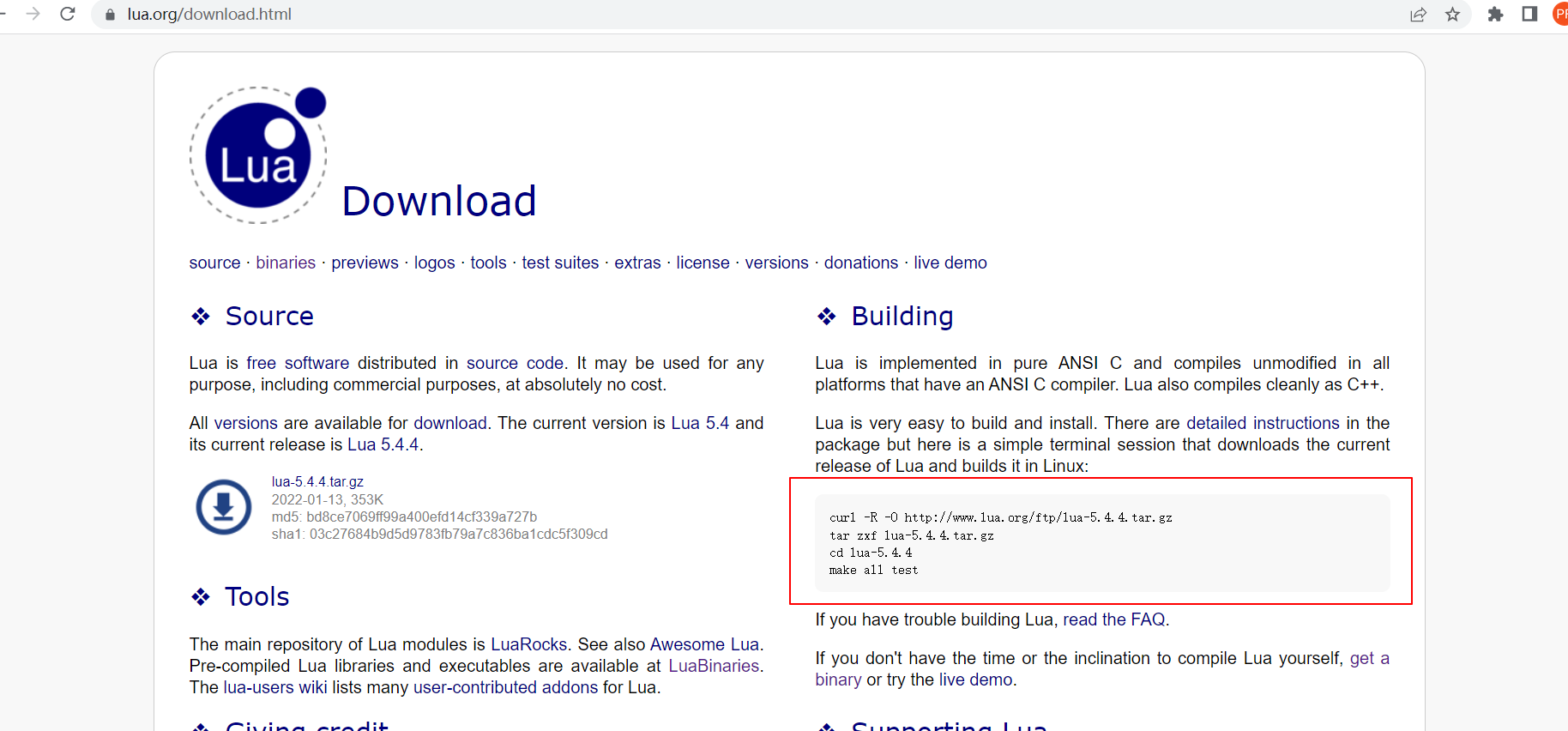
lua安装
lua安装 1.Lua介绍 特点:轻量、小巧。C语言开发。开源。 设计的目的:嵌入到应用程序当中,提供灵活的扩展和定制化的功能。 luanginx,luaredis。 2.windows安装lua windows上安装lua: 检查机器上是否有lua C:\U…...
博士毕业需要发表几篇cssci论文
大家好,今天来聊聊博士毕业需要发表几篇cssci论文,希望能给大家提供一点参考。 以下是针对论文重复率高的情况,提供一些修改建议和技巧: 博士毕业需要发表几篇CSSCI论文 背景介绍 CSSCI即“中文社会科学引文索引”,被…...

UDP报文格式详解
✏️✏️✏️各位看官好,今天给大家分享的是 传输层的另外一个重点协议——UDP。 清风的CSDN博客 🛩️🛩️🛩️希望我的文章能对你有所帮助,有不足的地方还请各位看官多多指教,大家一起学习交流࿰…...
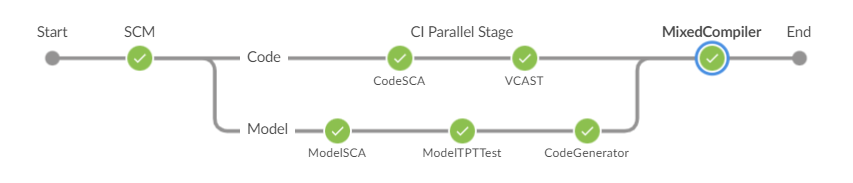
Python自动化测试如何自动生成测试用例?
汽车软件开发自动化测试攻略 随着软件开发在造车行业中占有越来越重要的地位,敏捷开发的思想在造车领域中也逐渐地被重视起来,随之而来的是整车厂对自动化测试需求越来越强烈。本文结合北汇在自动化测试方面的丰富经验,简单介绍一下实施自动…...
)
椋鸟C语言笔记#27:字符串数字提取(atoi、atol、atoll、atof)
萌新的学习笔记,写错了恳请斧正。 目录 atoi 模拟实现 atol与atoll(C99起) atof 合法的浮点值 返回值 使用示例 在stdlib.h中还有几个有意思的字符串函数 它们的功能是将字符串开头的数字提取出来 下面我们具体看一看这几个函数吧 …...

Git 命令使用总结
git init: 在当前目录创建一个新的空Git仓库。git clone [url]: 从远程仓库克隆一个项目到本地。git add [file]: 将文件添加到暂存区。git commit -m “message”: 提交暂存区的文件到本地仓库,并添加一条提交信息。git status: 查看当前工作区的状态(已…...
)
Linux常见面试题30题详细答案解析(二)
1. 如何使用Linux中的包管理器进行软件包依赖管理? Linux中的包管理器如apt、yum等可以自动处理软件包的依赖关系。当安装或升级软件包时,包管理器会自动解决软件包的依赖关系,确保所需的库和工具都已经安装。掌握如何使用包管理器进行依赖管…...
Linux查询指定时间点段日志Linux查询指定文件
Linux服务器高效查询日志查询文件 Ⅰ、常用几种日志查询语法Ⅱ、常用几种查询语法 Ⅰ、常用几种日志查询语法 #查询某日志前xx行日志 head -n 行数 日志文件名 #查询某日志后xx行日志 tail -n 行数 日志文件名 #查询固定时间点日志(前提是这个时间点确实有日志输出…...

2023年华为HCIA认证H12-811题库讲解
在VRP平台上,可以通过下面哪种方式返回到上一条历史命令?( ) A、Ctr1U B、Ctr1P C、左光标 D、上光标 试题答案:BD 试题解析:在VRP系统中,ctrlU为自定义快捷键,ct…...

MacOS上配置Jenkins开机自启动
之前文章有写过,如何在Windows环境下,通过vbsbat脚本的组合拳实现Jenkins的开机自启动,最近换了电脑,又要搭建Jenkins了,顺带整理分享下MacOS上配置Jenkins开机自启动的方法。 具体配置步骤: 打开终端应用…...
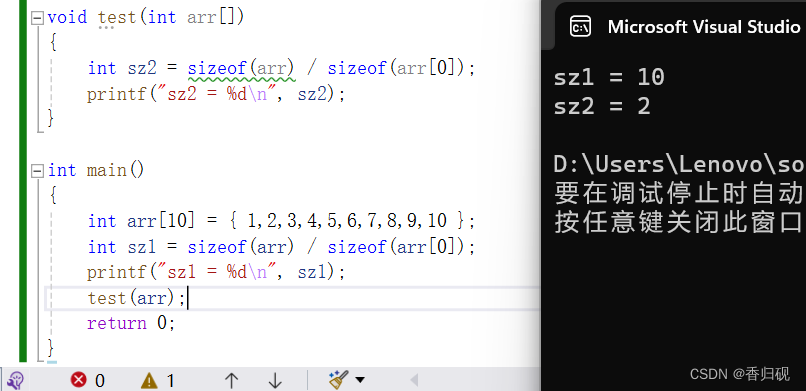
指针相关知识(入门)
通过前面的学习,我们已经对c语言有了一个初步的认识 接下来,我们继续学习。进入下一个阶段,指针。这个部分的知识较多,可能学习起来有些吃力,但是,从简到难,我们慢慢学习。 一.指针的概念 导入…...
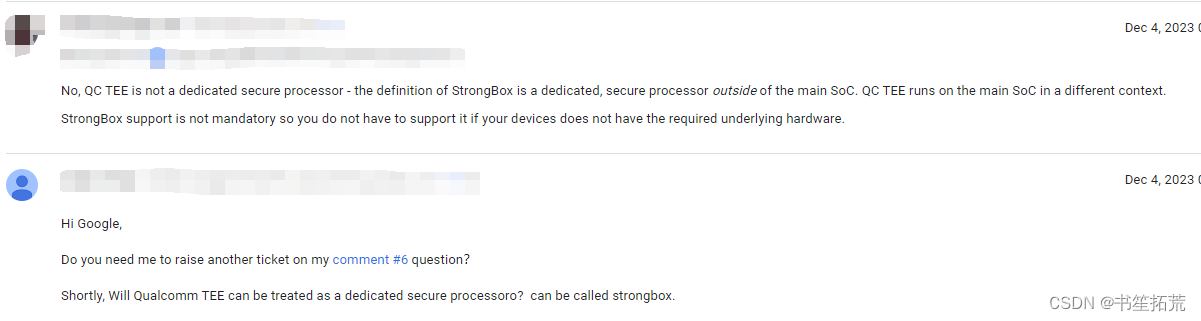
我的NPI项目之Android 安全系列 -- Android Strongbox 初识
从Android9(Pie)开始,Google强烈建议支持Strongbox. 具体描述如下: 一直到目前的Android14. 对应的内容也一并贴出来: 说人话就是Android开始通过独立于主SoC的单元进行密钥存储了。 通常,这样的单元就是我们通常称作的Secure Element(SE)&am…...
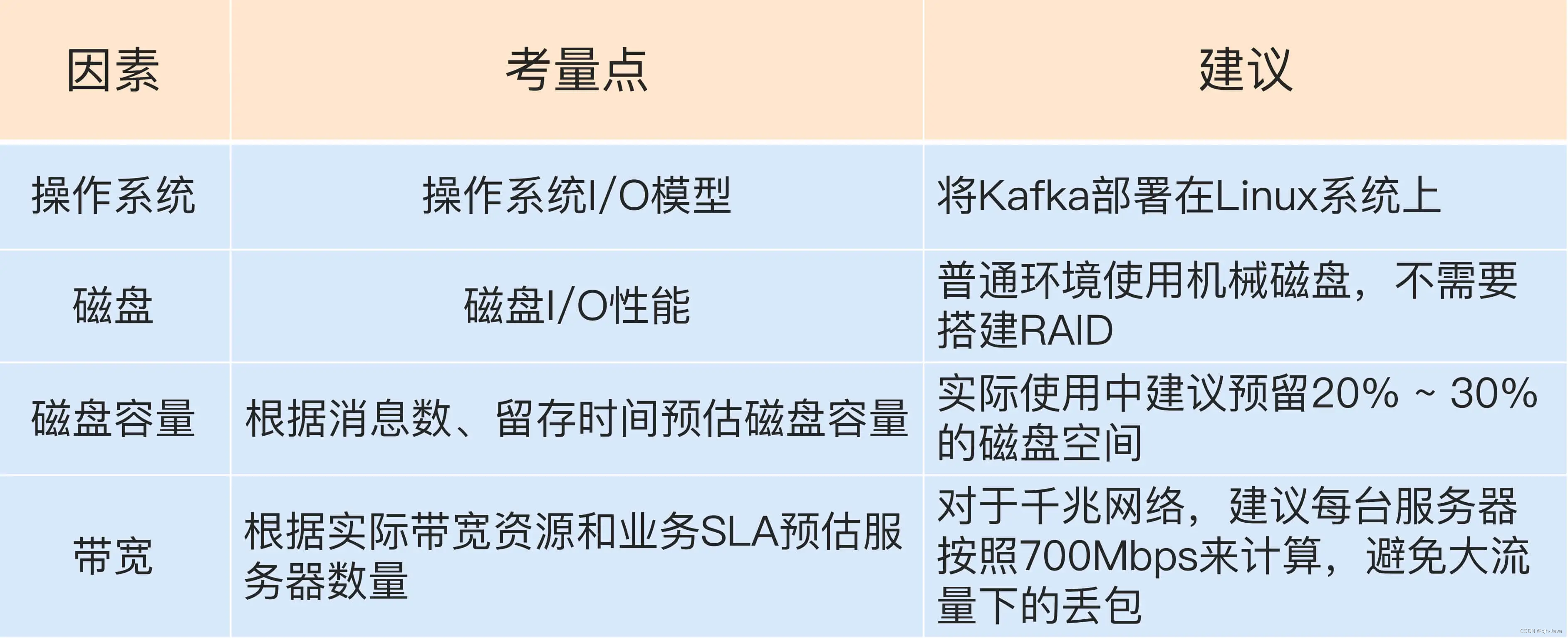
3、Kafka 线上集群部署方案怎么做?
文章目录 1、操作系统的选择1.1、I/O 模型的使用1.2、数据网络传输效率1.3、社区支持度 2、磁盘的选择3、磁盘容量的规划3.1、举例思考本问题:3.2、计算一下:3.3、规划磁盘容量时你需要考虑下面这几个元素: 4、带宽规划4.1、计算 总结 1、操作…...

【Oracle】常用数据库sql记录
文章目录 1、获取指定日期所在年份2、获取指定日期所在月份3、获取指定日期去年同期日期4、获取指定日期所在年份的总天数5、获取年初到指定日期的天数6、除法运算7、递归查询8、REPLACE函数9、DECODE 函数10、聚合函数11、窗口函数11.1 ROW_NUMBER函数11.2 RANK函数11.3 LEAD …...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
