力扣5. 最长回文子串
动态规划
- 思路:
- 假设 dp[i][j] 为字符串 (i, j) 子串是否为回文的结果;
- 那么 dp[i][j] = dp[i + 1][j - 1] 且 (s[i] == s[j]);
- 长度为1的字符串都是回文;
- 原字符串长度为1,是回文;
- 原字符串子串长度为1,即 i = j,dp[i][i] = true;
- 使用 begin 变量记录最长时的子串左边界,maxLen 缓存最长回文串的长度;
- 遍历迭代计算出所有 dp[i][j] 的值:
- 迭代子串长度 len,同时从左边界遍历;
class Solution {
public:string longestPalindrome(string s) {int size = s.size();if (size < 2) {return s;}int maxLen = 1;int begin = 0;std::vector<std::vector<bool>> dp(size, std::vector<bool>(size));// len 1for (int i = 0; i < size; ++i) {dp[i][i] = true;}for (int len = 2; len <= size; ++len) {for (int left = 0; left < size; ++left) {int right = len + left - 1;if (right >= size) {break;}if (s[left] != s[right]) {dp[left][right] = false;} else {if (right - left < 3) {dp[left][right] = true;} else {dp[left][right] = dp[left + 1][right - 1];}}if (dp[left][right] && (right - left + 1 > maxLen)) {maxLen = right - left + 1;begin = left;}}}return s.substr(begin, maxLen);}
};相关文章:

力扣5. 最长回文子串
动态规划 思路: 假设 dp[i][j] 为字符串 (i, j) 子串是否为回文的结果;那么 dp[i][j] dp[i 1][j - 1] 且 (s[i] s[j]);长度为1的字符串都是回文; 原字符串长度为1,是回文;原字符串子串长度为1ÿ…...

肆[4],函数VectorToHomMat2d/AffineTransPoint2d
函数VectorToHomMat2d C形式 LIntExport void VectorToHomMat2d( const HTuple& Px, const HTuple& Py, const HTuple& Qx, const HTuple& Qy, HTuple* HomMat2D);//参数1:图像坐标X数组 //参数2:图像坐标Y数组 //参数3:世界坐标X数组 //参数4:世界坐标Y…...

下载文件 后端返回给前端 response header 响应头
当浏览器在请求资源时,会通过http返回头中的content-type决定如何显示/处理将要加载的数据,如果这个类型浏览器能够支持阅览,浏览器就会直接展示该资源,比如png、jpeg、video等格式。在某些下载文件的场景中,服务端可能…...
lvs负载均集群
目录 NAT模式 LVS负载均衡群集部署 1.部署共享存储 2.配置节点服务器 192.168.17.130 编辑 192.168.17.133 3.配置负载调度器 4.测试效果 NAT模式 LVS负载均衡群集部署 负载调度器:内网关 ens33:192.168.17.70,外网关 ens36&#x…...
luttuce(RedisTempate)实现hash expire lua脚本
话不多说先放脚本: local argv ARGV local length #argv if length > 0 then local unpackArgs {} for i 1, length - 1 dotable.insert(unpackArgs, argv[i]) end if redis.call(exists, KEYS[1]) 1 thenredis.call(del, KEYS[1])redis.call(hset, KEYS[…...

【Xamarin】WebView连接局域网自动跳转外部浏览器问题的解决
xamarin在中国用的很少,但也有一些独到之处。例如用惯了Visual Studio的就很合适。而且类Java开发,几乎没什么障碍。 protected override void OnCreate(Bundle savedInstanceState) {base.OnCreate(savedInstanceState);Xamarin.Essentials.Platform.I…...
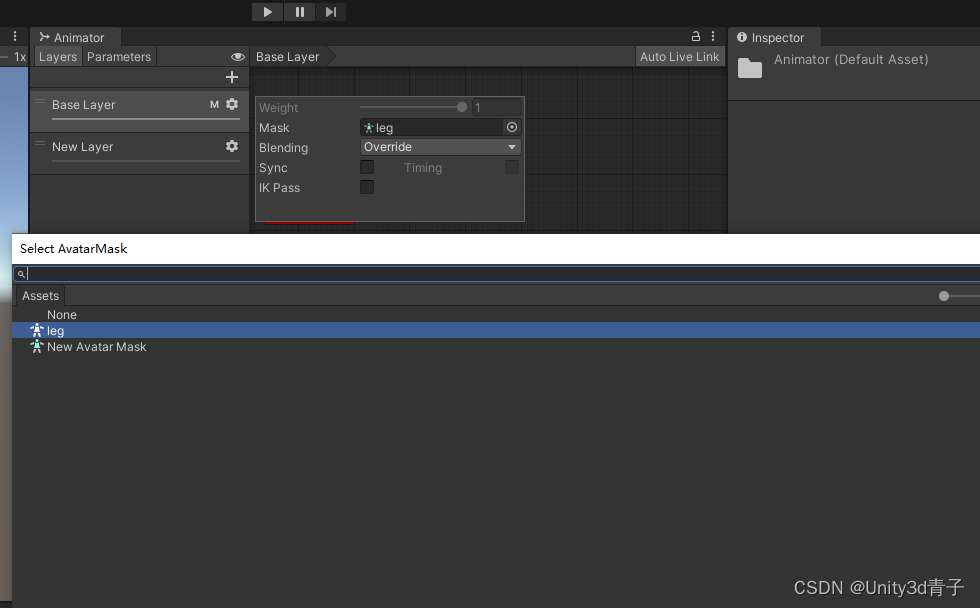
【Unity动画】实现不同的肢体动作自由搭配播放Layer+Avatar Mask
这个教程教你学会使用Unity 动画层配合布偶遮罩(AvaterMask) 实现从2个动画身上只保留部分肢体动作,然后搭配播放 例如:一个正常跑的动画片段,我只保留腿部动作,形成一个层叫Run_leg 然后在从一个攻击动作…...
转换为二进制)
将0x06(16进制)转换为二进制
将0x06(16进制)转换为二进制,可以按照如下步骤进行: 1. 将0x06中的字母"0x"去除。 2. 将数字"06"中的数字"0"去除。 3. 将数字"06"转换为二进制。 根据步骤1和步骤2,去除&q…...

考PRINCE2有用么?有PMP证书了还需要考PRINCE2吗?
有用的,PMP相当于是理论,PRINCE2是实践,对小白来说pmp考后再考一个prince2是很好的选择,对项目管理的小白来说更好入门。 先来说下 prince 2 和 pmp 的区别 一、prince 2 是什么?跟PMP有什么区别? prince…...

06进程间关系-学习笔记
Orphan Process孤儿进程 父进程先于子进程退出,子进程失去托管,这种子进程统称为孤儿进程 失效进程(孤儿进程):导致内存泄漏,影响新进程的创建孤儿进程的危害不可预测,如果一个孤儿进程持续的申…...

Vue的动画方式有几种
Vue的动画方式有几种? Vue的动画方式主要分成两大类,一类是CSS动画,一类是JS动画 CSS动画中包含transition以及animation,但在Vue中只需要通过transition封装组件实现。 CSS动画的类名主要包括:v-enter、v-enter-acti…...

PyTorch: 基于【VGG16】处理MNIST数据集的图像分类任务【准确率98.9%+】
目录 引言在Conda虚拟环境下安装pytorch步骤一:利用代码自动下载mnist数据集步骤二:搭建基于VGG16的图像分类模型步骤三:训练模型步骤四:测试模型运行结果后续模型的优化和改进建议完整代码结束语 引言 在本博客中,小…...
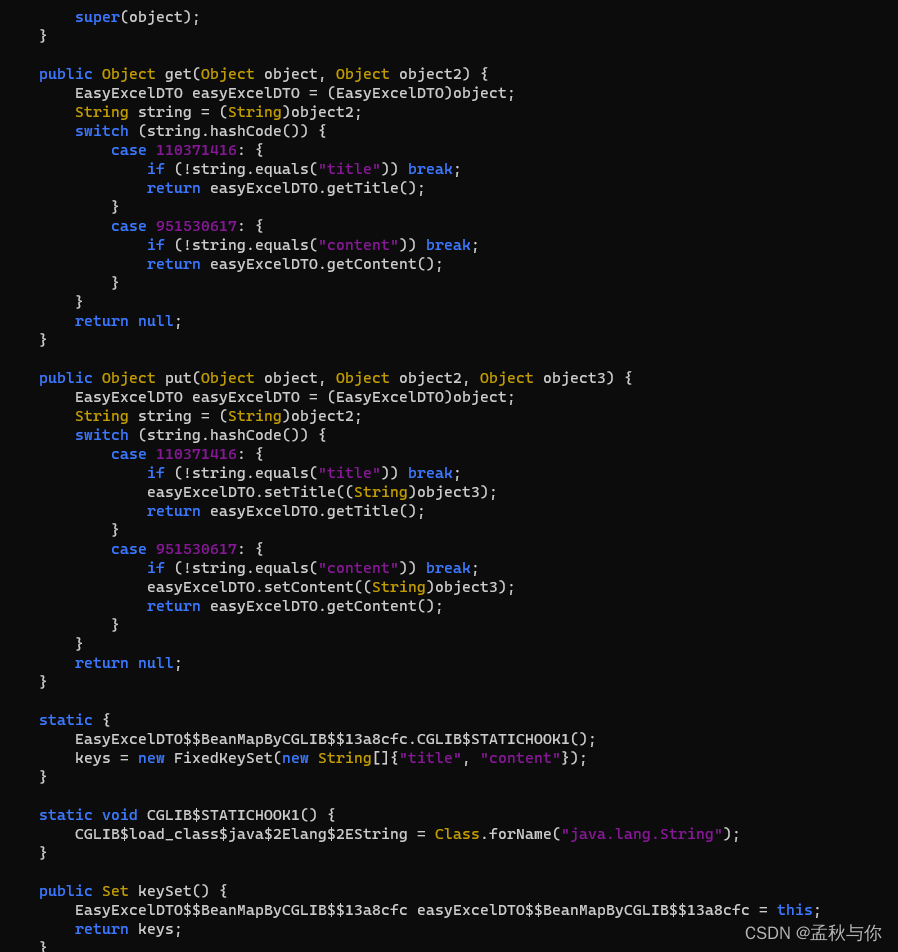
【lombok】从easyExcel read不到值到cglib @Accessors(chain = true)隐藏的大坑
背景: 在一次使用easyExcel.read 读取excel时,发现实体类字段没有值,在反复测试后,发现去掉Accessors(chain true)就正常了,为了验证原因,进行了一次代码跟踪 由于调用链路特别长,只列举出部分代码&#x…...

1-SaaS通识
云计算 讲SaaS必须先讲云计算。云计算通过互联网提供计算服务,包括服务器、存储、数据库、网络、应用等,采用按需付费的定价模式。 云计算的4种部署模式 公有云:由云服务商拥有和管理,就好比水电,居民共享ÿ…...

Spring Boot实现接口幂等
Spring Boot实现接口幂等 1、pom依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http:…...
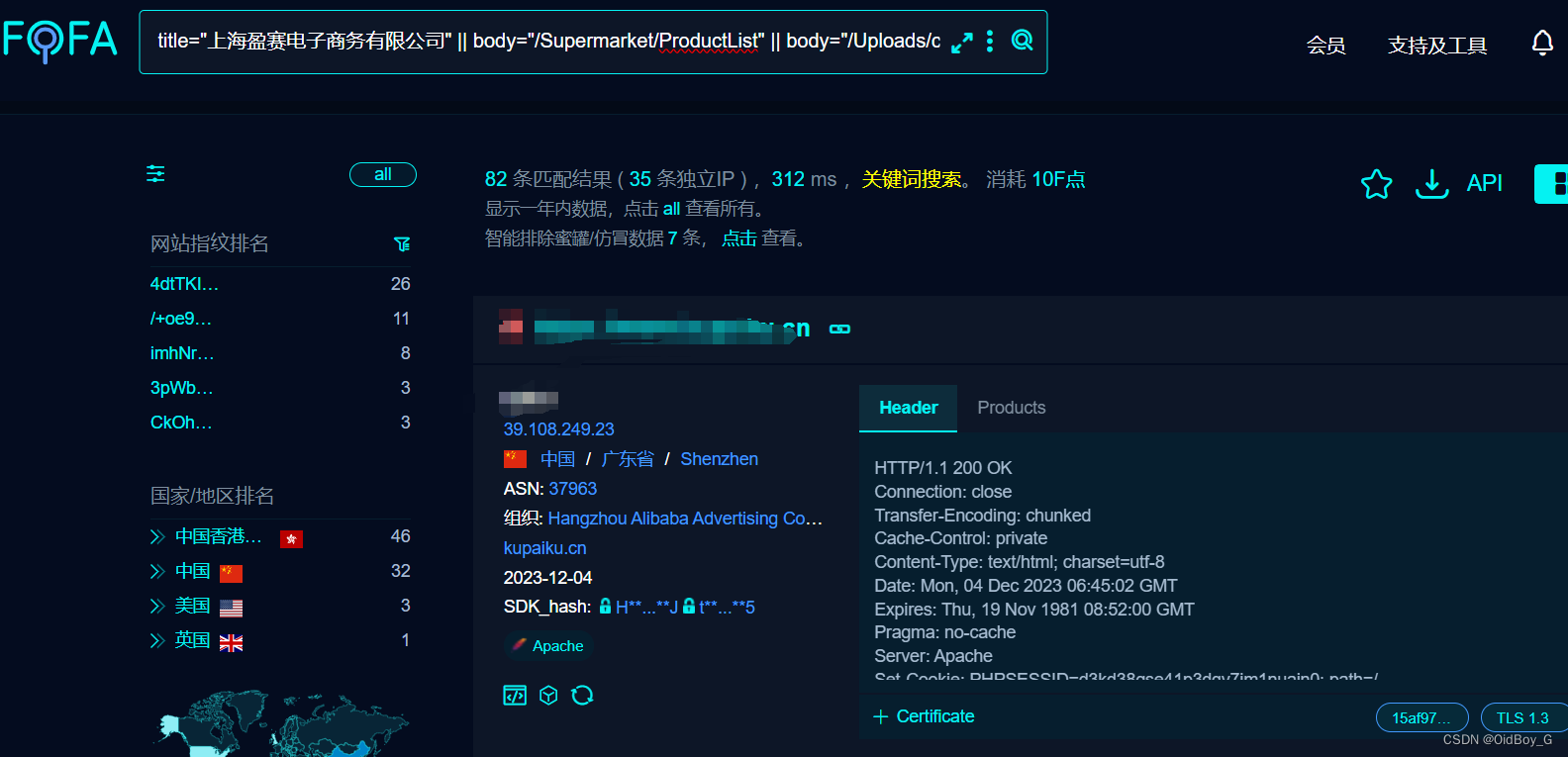
ShopsN commentUpload 文件上传漏洞复现
0x01 产品简介 ShopsN 是一款符合企业级商用标准全功能的真正允许免费商业用途的开源网店全网系统。 0x02 漏洞概述 ShopsN commentUpload 接口处存在任意文件上传漏洞,攻击者可以利用文件上传漏洞执行恶意代码、写入后门、读取敏感文件,从而可能导致服务器受到攻击并被控…...

【Qt5】ui文件最后会变成头文件
2023年12月14日,周四下午 我也是今天下午偶然间发现这个的 在使用Qt的uic(User Interface Compiler)工具编译ui文件时,会生成对应的头文件。 在Qt中,ui文件是用于描述用户界面的XML文件,而头文件是用于在…...
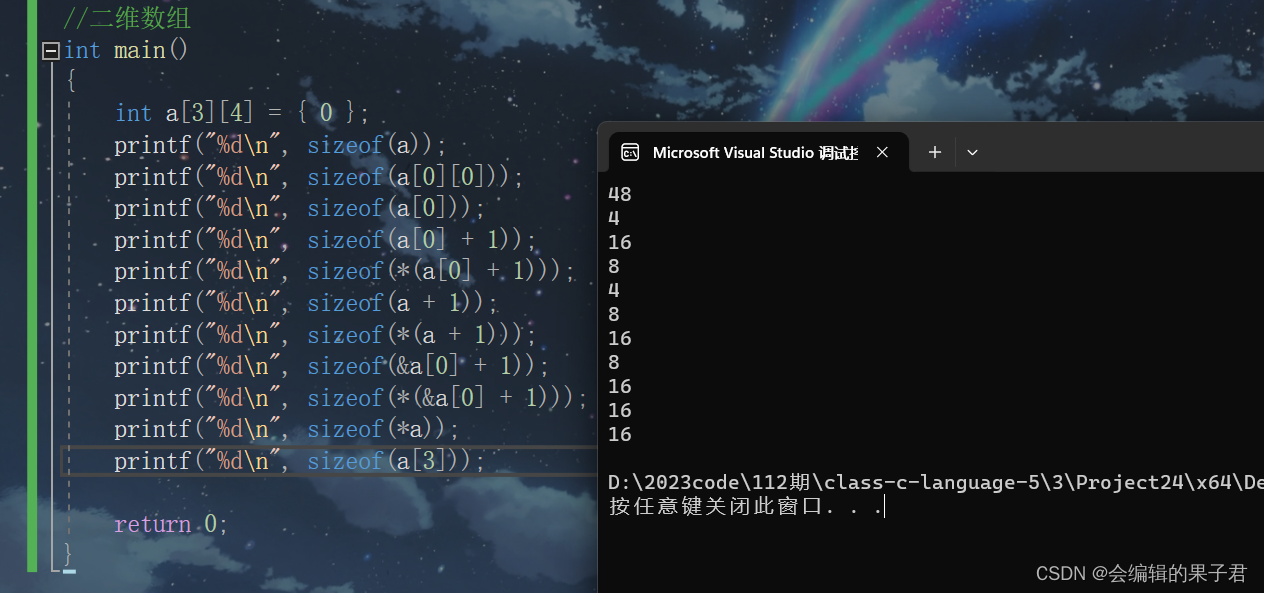
数组笔试题解析(下)
数组面试题解析 字符数组 (一) 我们上一篇文章学习了一维数组的面试题解析内容和字符数组的部分内容,我们这篇文章讲解一下字符数组和指针剩余面试题的解析内容,那现在,我们开始吧。 我们继续看一组字符数组的面试…...
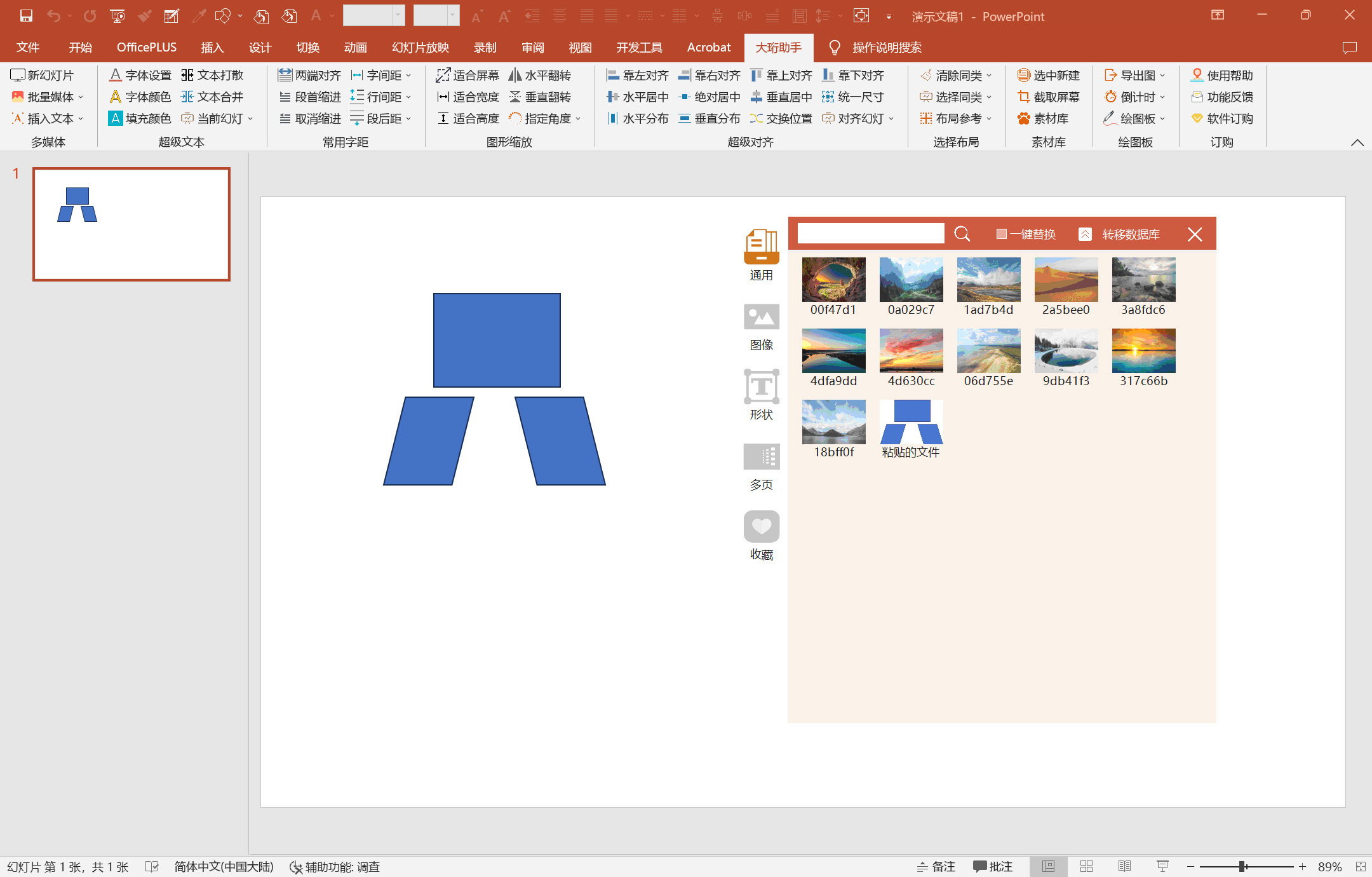
PPT插件-好用的插件-图形缩放-大珩助手
图形缩放 包括适合屏幕、适合宽度、适合高度、水平翻转、垂直翻转、指定角度,可同时对多个形状进行操作 适合屏幕 一键设置图像、文本、形状的长宽尺寸与当前幻灯片一致 适合宽度 一键设置图像、文本、形状的宽度尺寸与当前幻灯片一致 适合高度 一键设置图像…...

五:爬虫-数据解析之xpath解析
五:数据解析之xpath解析 1.xpath介绍: xpath是XML路径语言,它可以用来确定xml文档中的元素位置,通过元素路径来完成对元素的查找,HTML就是XML的一种实现方式,所以xpath是一种非常强大的定位方式 XPa…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
