设计模式——组合模式(结构型)
引言
组合模式是一种结构型设计模式, 你可以使用它将对象组合成树状结构, 并且能像使用独立对象一样使用它们。

问题
如果应用的核心模型能用树状结构表示, 在应用中使用组合模式才有价值。
例如, 你有两类对象: 产品和 盒子 。 一个盒子中可以包含多个 产品或者几个较小的 盒子 。 这些小 盒子中同样可以包含一些 产品或更小的 盒子 , 以此类推。
假设你希望在这些类的基础上开发一个定购系统。 订单中可以包含无包装的简单产品, 也可以包含装满产品的盒子…… 以及其他盒子。 此时你会如何计算每张订单的总价格呢?
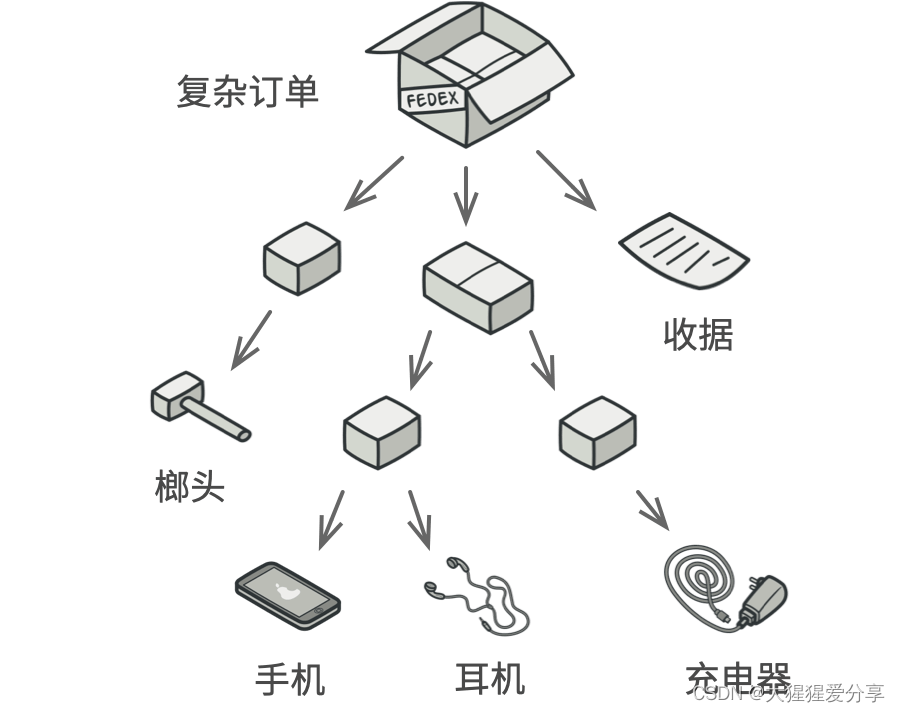
订单中可能包括各种产品,这些产品放置在盒子中,然后又被放入一层又一层更大的盒子中。整个结构看上去像是一棵倒过来的树。
你可以尝试直接计算: 打开所有盒子, 找到每件产品, 然后计算总价。 这在真实世界中或许可行, 但在程序中, 你并不能简单地使用循环语句来完成该工作。 你必须事先知道所有 产品和 盒子的类别, 所有盒子的嵌套层数以及其他繁杂的细节信息。 因此, 直接计算极不方便, 甚至完全不可行。
解决方案
组合模式建议使用一个通用接口来与 产品和 盒子进行交互, 并且在该接口中声明一个计算总价的方法。
那么方法该如何设计呢? 对于一个产品, 该方法直接返回其价格; 对于一个盒子, 该方法遍历盒子中的所有项目, 询问每个项目的价格, 然后返回该盒子的总价格。 如果其中某个项目是小一号的盒子, 那么当前盒子也会遍历其中的所有项目, 以此类推, 直到计算出所有内部组成部分的价格。 你甚至可以在盒子的最终价格中增加额外费用, 作为该盒子的包装费用。

该方式的最大优点在于你无需了解构成树状结构的对象的具体类。 你也无需了解对象是简单的产品还是复杂的盒子。 你只需调用通用接口以相同的方式对其进行处理即可。 当你调用该方法后, 对象会将请求沿着树结构传递下去。
真实世界类比
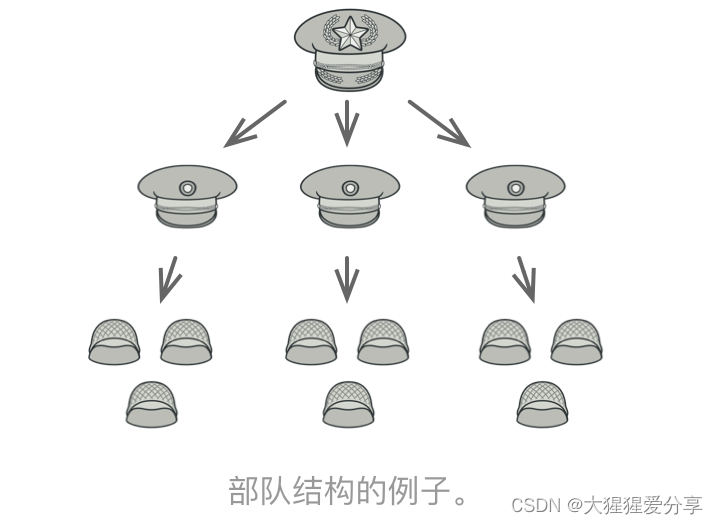
大部分国家的军队都采用层次结构管理。 每支部队包括几个师, 师由旅构成, 旅由团构成, 团可以继续划分为排。 最后, 每个排由一小队实实在在的士兵组成。 军事命令由最高层下达, 通过每个层级传递, 直到每位士兵都知道自己应该服从的命令。
组合模式结构
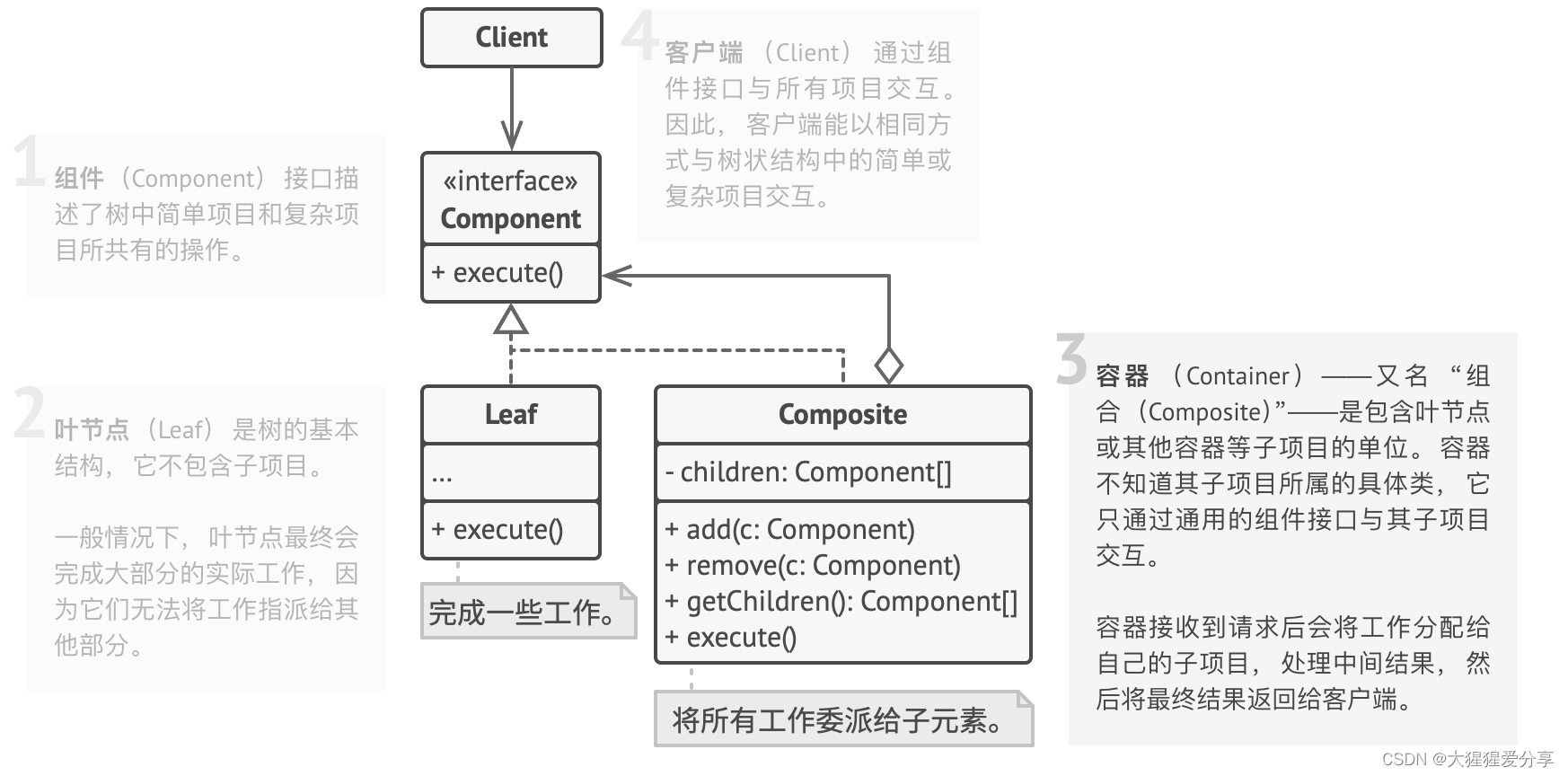
伪代码
在本例中, 我们将借助组合模式帮助你在图形编辑器中实现一系列的几何图形。
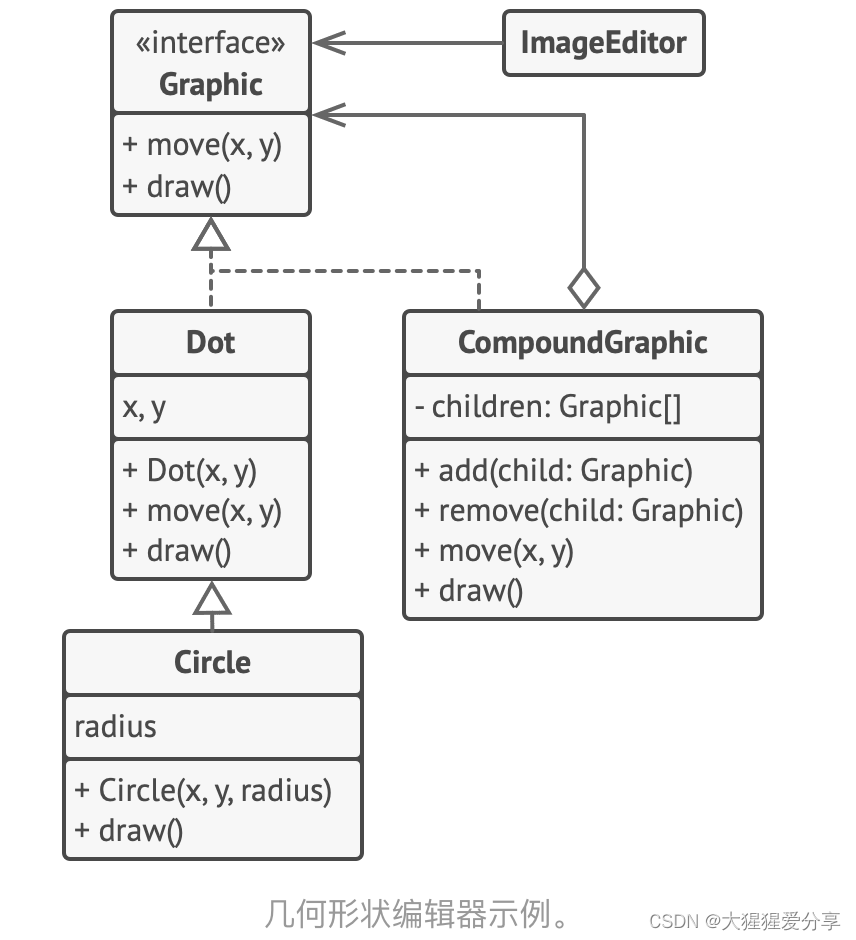
组合图形CompoundGraphic是一个容器, 它可以由多个包括容器在内的子图形构成。 组合图形与简单图形拥有相同的方法。 但是, 组合图形自身并不完成具体工作, 而是将请求递归地传递给自己的子项目, 然后 “汇总” 结果。
通过所有图形类所共有的接口, 客户端代码可以与所有图形互动。 因此, 客户端不知道与其交互的是简单图形还是组合图形。 客户端可以与非常复杂的对象结构进行交互, 而无需与组成该结构的实体类紧密耦合。
// 组件接口会声明组合中简单和复杂对象的通用操作。
interface Graphic ismethod move(x, y)method draw()// 叶节点类代表组合的终端对象。叶节点对象中不能包含任何子对象。叶节点对象
// 通常会完成实际的工作,组合对象则仅会将工作委派给自己的子部件。
class Dot implements Graphic isfield x, yconstructor Dot(x, y) { …… }method move(x, y) isthis.x += x, this.y += ymethod draw() is// 在坐标位置(X,Y)处绘制一个点。// 所有组件类都可以扩展其他组件。
class Circle extends Dot isfield radiusconstructor Circle(x, y, radius) { …… }method draw() is// 在坐标位置(X,Y)处绘制一个半径为 R 的圆。// 组合类表示可能包含子项目的复杂组件。组合对象通常会将实际工作委派给子项
// 目,然后“汇总”结果。
class CompoundGraphic implements Graphic isfield children: array of Graphic// 组合对象可在其项目列表中添加或移除其他组件(简单的或复杂的皆可)。method add(child: Graphic) is// 在子项目数组中添加一个子项目。method remove(child: Graphic) is// 从子项目数组中移除一个子项目。method move(x, y) isforeach (child in children) dochild.move(x, y)// 组合会以特定的方式执行其主要逻辑。它会递归遍历所有子项目,并收集和// 汇总其结果。由于组合的子项目也会将调用传递给自己的子项目,以此类推,// 最后组合将会完成整个对象树的遍历工作。method draw() is// 1. 对于每个子部件:// - 绘制该部件。// - 更新边框坐标。// 2. 根据边框坐标绘制一个虚线长方形。// 客户端代码会通过基础接口与所有组件进行交互。这样一来,客户端代码便可同
// 时支持简单叶节点组件和复杂组件。
class ImageEditor isfield all: CompoundGraphicmethod load() isall = new CompoundGraphic()all.add(new Dot(1, 2))all.add(new Circle(5, 3, 10))// ……// 将所需组件组合为复杂的组合组件。method groupSelected(components: array of Graphic) isgroup = new CompoundGraphic()foreach (component in components) dogroup.add(component)all.remove(component)all.add(group)// 所有组件都将被绘制。all.draw()
组合模式适合应用场景
如果你需要实现树状对象结构, 可以使用组合模式。
组合模式为你提供了两种共享公共接口的基本元素类型: 简单叶节点和复杂容器。 容器中可以包含叶节点和其他容器。 这使得你可以构建树状嵌套递归对象结构。
如果你希望客户端代码以相同方式处理简单和复杂元素, 可以使用该模式。
组合模式中定义的所有元素共用同一个接口。 在这一接口的帮助下, 客户端不必在意其所使用的对象的具体类。
实现方式
-
确保应用的核心模型能够以树状结构表示。 尝试将其分解为简单元素和容器。 记住, 容器必须能够同时包含简单元素和其他容器。
-
声明组件接口及其一系列方法, 这些方法对简单和复杂元素都有意义。
-
创建一个叶节点类表示简单元素。 程序中可以有多个不同的叶节点类。
-
创建一个容器类表示复杂元素。 在该类中, 创建一个数组成员变量来存储对于其子元素的引用。 该数组必须能够同时保存叶节点和容器, 因此请确保将其声明为组合接口类型。
实现组件接口方法时, 记住容器应该将大部分工作交给其子元素来完成。
-
最后, 在容器中定义添加和删除子元素的方法。
记住, 这些操作可在组件接口中声明。 这将会违反接口隔离原则, 因为叶节点类中的这些方法为空。 但是, 这可以让客户端无差别地访问所有元素, 即使是组成树状结构的元素。
组合模式优缺点
- 你可以利用多态和递归机制更方便地使用复杂树结构。
- 开闭原则。 无需更改现有代码, 你就可以在应用中添加新元素, 使其成为对象树的一部分。
与其他模式的关系
-
桥接模式、 状态模式和策略模式 (在某种程度上包括适配器模式) 模式的接口非常相似。 实际上, 它们都基于组合模式——即将工作委派给其他对象, 不过也各自解决了不同的问题。 模式并不只是以特定方式组织代码的配方, 你还可以使用它们来和其他开发者讨论模式所解决的问题。
-
你可以在创建复杂组合树时使用生成器模式, 因为这可使其构造步骤以递归的方式运行。
-
责任链模式通常和组合模式结合使用。 在这种情况下, 叶组件接收到请求后, 可以将请求沿包含全体父组件的链一直传递至对象树的底部。
-
你可以使用迭代器模式来遍历组合树。
-
你可以使用访问者模式对整个组合树执行操作。
-
你可以使用享元模式实现组合树的共享叶节点以节省内存。
-
组合和装饰模式的结构图很相似, 因为两者都依赖递归组合来组织无限数量的对象。
装饰类似于组合, 但其只有一个子组件。 此外还有一个明显不同: 装饰为被封装对象添加了额外的职责, 组合仅对其子节点的结果进行了 “求和”。
但是, 模式也可以相互合作: 你可以使用装饰来扩展组合树中特定对象的行为。
-
大量使用组合和装饰的设计通常可从对于原型模式的使用中获益。 你可以通过该模式来复制复杂结构, 而非从零开始重新构造。
相关文章:

设计模式——组合模式(结构型)
引言 组合模式是一种结构型设计模式, 你可以使用它将对象组合成树状结构, 并且能像使用独立对象一样使用它们。 问题 如果应用的核心模型能用树状结构表示, 在应用中使用组合模式才有价值。 例如, 你有两类对象: …...

鸿蒙小车之多任务调度实验
说到鸿蒙我们都会想到华为mate60:遥遥领先!我们一直领先! 我们这个小车也是采用的是鸿蒙操作系统,学习鸿蒙小车,让你遥遥领先于你的同学。 文章目录 前言一、什么是任务?为什么要有任务二、任务的状态三、任…...
【报错栏】(vue)Module not found: Error: Can‘t resolve ‘element-ui‘ in xxx
Module not found: Error: Cant resolve element-ui in xxx 报错原因是: 未安装 element-ui 依赖 解决: npm install element-ui 运行...
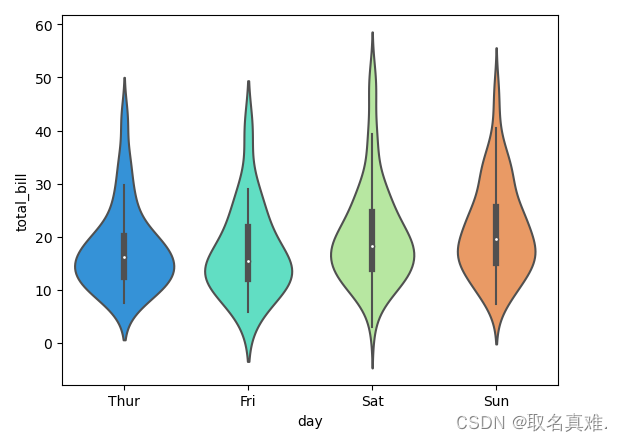
seaborn库图形进行数据分析(基于tips数据集)
Seaborn 是一个基于 matplotlib 的数据可视化库,可以用来绘制各种统计图表,包括散点图、条形图、折线图、箱线图等。Seaborn 提供了一些用于美化图表的默认样式和颜色主题,使得生成的图表更具有吸引力。下面是一些 Seaborn 库的常用功能和用法…...
AC843. n皇后问题--60
我们只需要把蓝色的往上移动就行了 if(!col[i][j]&&!dg[ui]&&!udg[])//1y(i)向下,x(u)向右为正。yxb的by-x一定>0,y-xb的bxy可能>0,这个不考虑,只看-bxy....

Js WebSocket类,收发Json,带心跳,断线重连
如题 心跳:4秒发一次 断线:2秒后自动重连 收发:发送和返回json,处理粘包断包等情况,json字符串最大长度9999 缓存:未连接时,自动缓存100个包,当连接时会自动发出 JS代码 var MyWeb…...

VBA技术资料MF96:单字段多条件高级筛选
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...
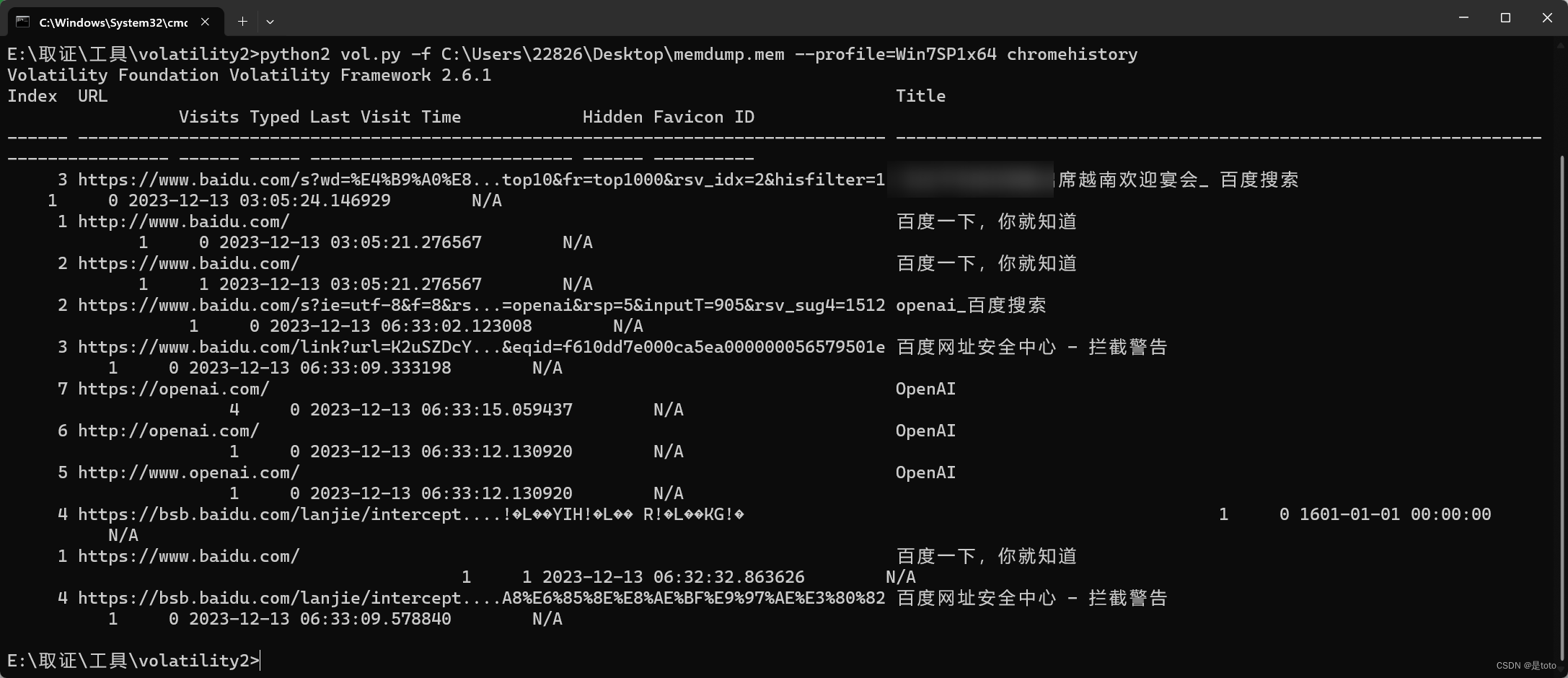
电子取证中Chrome各版本解密Cookies、LoginData账号密码、历史记录
文章目录 1.前置知识点2.对于80.X以前版本的解密拿masterkey的几种方法方法一 直接在目标机器运行Mimikatz提取方法二 转储lsass.exe 进程从内存提取masterkey方法三 导出SAM注册表 提取user hash 解密masterkey文件(有点麻烦不太推荐)方法四 已知用户密…...

Axure元件基本介绍进阶
Axure元件基本介绍进阶 1.Axure元件基本介绍1.在 Axure 中,元件是构建原型的基本构成单元,能够帮助设计师快速创建、重复使用和管理设计元素。以下是 Axure 中元件的基本介绍:1.基本元件: 2.基本元件的使用一.【举例说明】积木&am…...

安卓11添加切换以太网动态静态方法
客户要在app中自由切换动态,静态方法,直接把系统jar-api给他搞了半天搞不定,只有在系统里给他实现一个接口,方法如下: Index: packages/apps/Settings/AndroidManifest.xml--- packages/apps/Settings/AndroidManifes…...
初级数据结构(五)——树和二叉树的概念
文中代码源文件已上传:数据结构源码 <-上一篇 初级数据结构(四)——队列 | NULL 下一篇-> 1、树结构(Tree) 1.1、树结构的特点 自然界中的树由根部开始向上生长,随机长出分支&…...
问题)
pdf读取内容缺失(漏字/文字丢失)问题
项目中遇到pdf文件漏字,由于文件涉密,不能展示,简单描述一下: 比如原pff中 姓名:张三 读取结果中:空白:张三 即:原文件说是银行出具的打款证明,银行内部设置了文件权限&a…...

c#面试基础语法——现有⼀个整数number,请写⼀个⽅法判断这个整数是否是2的N次⽅
1.number%20 取余(取模)只能判断number是不是2的倍数但不一定是2的N次方,如:6%20但是他并不是2的N次方 2.(number&(number-1))0 原理:如果number是2的N次方则表示2进制位只有一位是1。如:2 (…...
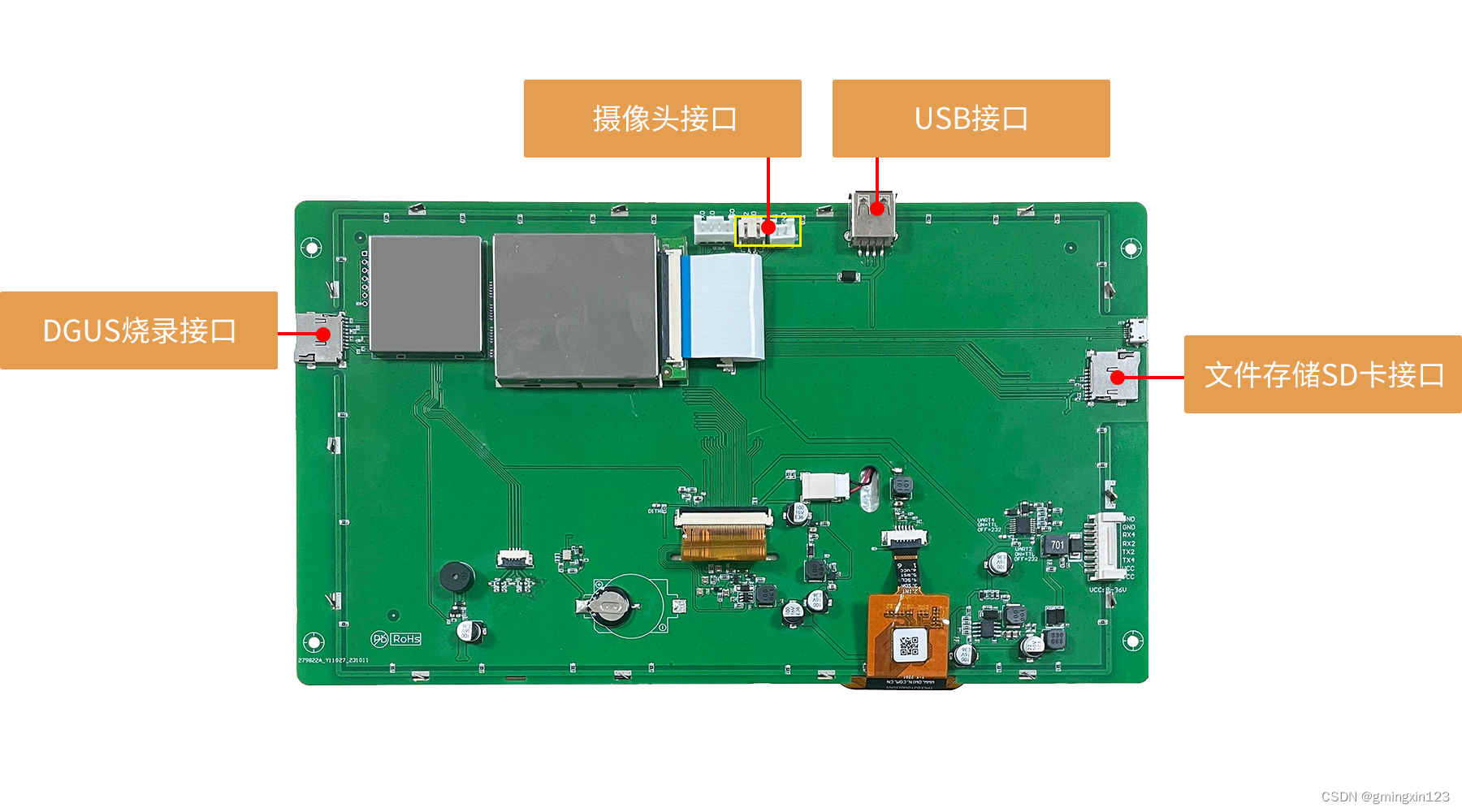
27系列DGUS智能屏发布:可实时播放高清模拟信号摄像头视频
针对高清晰度的模拟信号摄像头视频画面的显示需求,迪文特推出27系列DGUS智能屏。该系列智能屏可适配常见的AHD摄像头、CVBS摄像头,支持单路1080P高清显示、两路720P同屏显示(同一类型摄像头)。用户通过DGUS简单开发即可实现摄像头…...

YOLOv8改进 | 2023主干篇 | 替换LSKNet遥感目标检测主干 (附代码+修改教程+结构讲解)
一、本文介绍 本文给大家带来的改进内容是LSKNet(Large Kernel Selection, LK Selection),其是一种专为遥感目标检测设计的网络架构,其核心思想是动态调整其大的空间感受野,以更好地捕捉遥感场景中不同对象的范围上下…...

【工具】VUE 前端列表拖拽功能代码
【工具】VUE 前端列表拖拽功能代码 使用组件 yarn add sortablejs --save Sortable.js中文网 (sortablejs.com) 以下代码只是举个例子, 大家可以举一反三去实现各自的业务功能 <template><div><el-button type"primary" click"切换…...
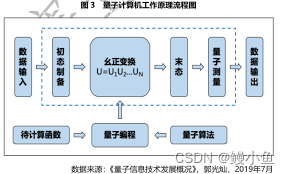
人工智能与量子计算:开启未知领域的智慧之旅
导言 人工智能与量子计算的结合是科技领域的一场创新盛宴,引领我们进入了探索未知领域的新时代。本文将深入研究人工智能与量子计算的交汇点,探讨其原理、应用以及对计算领域的深远影响。 量子计算的崛起为人工智能领域注入了新的活力,开启了…...

2023了,前端实现AI电子秤思路分析
前景小知识: 这几年ai这个话题非常火爆,笔者从事零售行业软件开发也接到了新需求,希望实现ai电子秤,老规矩,先看需求 举个栗子: 或许,你已经留意到,当你在某些大型超市超市或生鲜类…...

CSS学习
CSS学习 1. 什么是css?2.css引入方式2.1 内嵌式2.2 外联式2.3 行内式2.4 引入方式特点 3. 基础选择器3.1 标签选择器3.2 类选择器3.3 id选择器3.4 通配符选择器 4. 文字基本样式4.1 字体样式4.1.1 字体大小4.1.2 字体粗细4.1.3 倾斜4.1.4 字体4.1.5 字体font相关属性连写 4.2 …...

Flask基本用法:一个HelloWorld,搭建服务、发起请求
目录 1、简介 2、安装 3、Flask使用示例 参考 1、简介 官网文档 Flask是一个轻量的web服务框架,我们可以利用它快速搭建一个服务,对外提供接口,其他人可以轻松调用我们的服务。这对算法工程师来说比较关键,我们通常不擅长搞开发…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
