使用 Python 使用贝叶斯神经网络从理论到实践
一、说明
在本文中,我们了解了如何构建一个机器学习模型,该模型结合了神经网络的强大功能,并且仍然保持概率方法进行预测。为了做到这一点,我们可以构建所谓的贝叶斯神经网络。
这个想法不是优化神经网络的损失,而是优化无限神经网络的损失。换句话说,我们正在优化给定数据集的模型参数的概率分布。
我们使用损失函数来做到这一点,该函数包含称为 Kullback-Leibler 背离的指标。这用于计算两个分布之间的距离。
在优化了损失函数之后,我们能够使用概率模型。 这意味着,如果我们重复这个模型两次,我们会得到两个不同的结果,如果我们重复 10k 次,我们就能提取出结果的稳健统计分布。
我们使用 torch 和一个名为 torchbnn 的库来实现了这一点。我们构建了简单的回归任务,并使用两层前馈神经网络对其进行了求解。
二、物理学家和工程学家
物理学和工程学是两门截然不同的科学,它们都渴望了解自然和模拟自然的能力。
物理学家的方法更具理论性。物理学家观察世界,并试图以最准确的方式对其进行建模。物理学家建模的现实是不完美的,并且有近似值,但一旦我们考虑这些不完美,现实就会变得整洁、完美和优雅。
工程师的方法更实用。工程师意识到物理学家模型的所有局限性,并试图使实验室中的体验尽可能流畅。工程师可能会做更残酷的近似(例如 pi = 3),但它的近似实际上在现实生活中的实验中更有效。
戈登·林赛·格莱格(Gordon Lindsay Glegg)的这句话总结了工程师的实践方法与物理学家优雅的理论方法之间的这种差异:
科学家可以发现一颗新星,但他不能制造一颗新星。他必须请工程师为他做这件事。
在研究人员的日常生活中,它有点像这样工作。物理学家是对特定现象有理论的人。工程师是科学家,可以设置实验并查看理论是否有效。
实际上,当我开始从物理学家到工程师的转变时,我经常被问到的一个问题是:
“好的,你的模型似乎有效......但它有多强大呢?
这是一个典型的工程师问题。
当你有一个物理模型时,在一定条件下,这个模型在理论上是完美的。

皮耶罗·帕亚伦加
尽管如此,当你进行实验时,存在一定程度的误差,你必须能够正确地估计它。
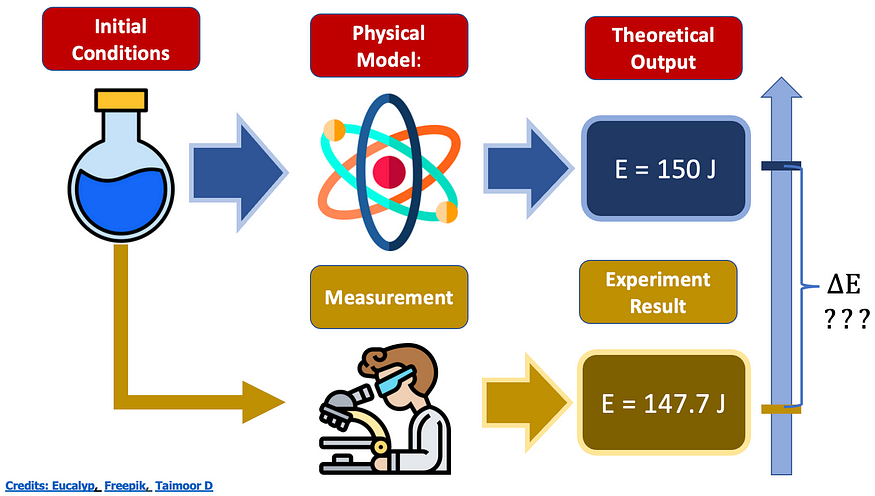
图片由作者提供
在我们正在做的这个具体例子中,我们如何估计理论输出和实验结果之间的能量差异?
两个选项:
一个。如果模型是确定性的,则可以按某个增量更改初始条件(例如,将该确定性规则应用于输入的嘈杂版本)
B.如果模型是概率的,对于某些给定的输入,您可以从输出中提取一些统计信息(例如平均值、标准差、不确定性边界......
现在让我们进入机器学习的语言。 在此特定情况下:
一个。如果机器学习模型是确定性的,我们可以通过打乱训练集和验证集来测试其鲁棒性。
B.如果机器学习模型是概率的,对于某些给定的输入,你可以从输出中提取一些统计信息(例如平均值、标准差、不确定性边界......
现在,假设我们要使用的模型是神经网络。
第一个问题:你需要神经网络吗?如果答案是肯定的,那么你必须使用它(你不说)。问题:
“你的机器学习模型健壮吗?”
神经网络的原始定义是“纯确定性”。
我们可以对训练集、验证集和测试集进行洗牌,但我们需要考虑到神经网络可能需要很长时间来训练,如果我们想进行多个测试(假设 CV = 10,000),那么,您可能需要等待一段时间。
我们需要考虑的另一件事是,神经网络使用一种称为梯度下降的算法进行优化。这个想法是,我们从参数空间中的一个点开始,顾名思义,沿着损失的负梯度指示的方向下降。理想情况下,这将把我们带到一个全局最小值(剧透:它实际上从来都不是全局的)。
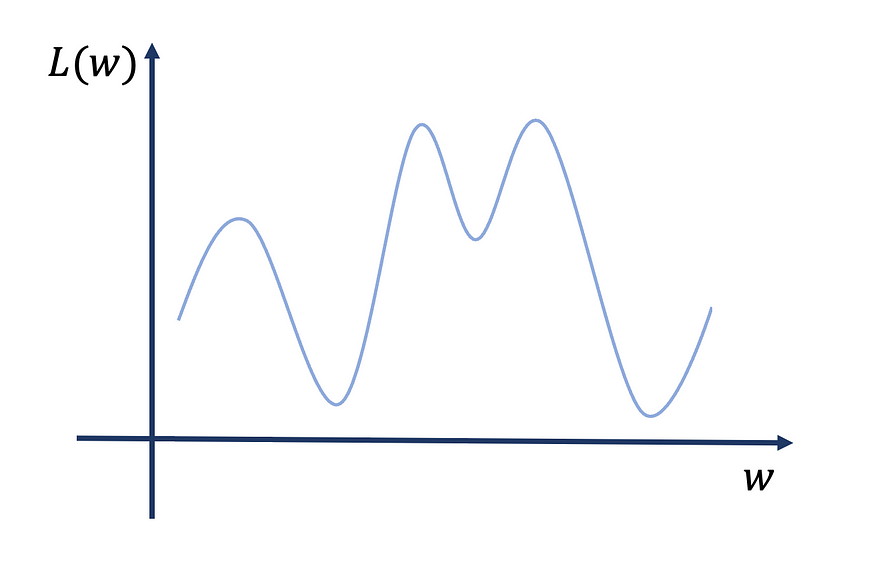
对于不切实际的简单一维损失函数,理想的情况如下:

现在,在这种情况下,如果我们改变起点,我们仍然收敛到唯一的全局最小值。
更现实的情况是这样的:
因此,如果我们从不同的起点随机重启训练算法,我们会收敛到不同的局部最小值。
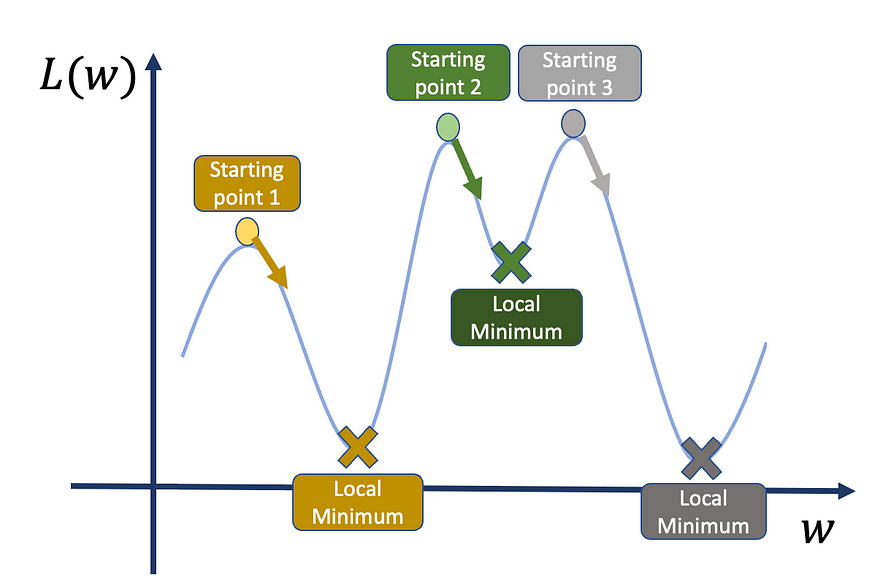
因此,如果我们从点 1 或点 3 开始,我们得到的点比起点 2 低。
损失函数可能充满局部最小值,因此找到真正的全局最小值可能是一项艰巨的任务。我们可以做的另一件事是从不同的起点重新开始训练,并比较损失函数值。这种方法和以前一样,我们遇到了同样的问题:我们只能做这么多次。
有一种更强大、更严格、更优雅的方法可以以概率的方式使用神经网络的相同计算能力;它称为贝叶斯神经网络。
在本文中,我们将学习:
- 贝叶斯神经网络背后的理念
- 贝叶斯神经网络背后的数学公式
- 使用 Python 实现贝叶斯神经网络(更具体地说是 Pytorch)
- 如何使用贝叶斯神经网络解决回归问题
让我们开始吧!
三、什么是贝叶斯神经网络?
正如我们之前所说,贝叶斯神经网络的思想是向典型的神经网络添加概率“感觉”。我们是怎么做到的?
在理解贝叶斯神经网络之前,我们可能应该回顾一下贝叶斯定理。
查看贝叶斯定理的一个非常有效的方法如下:
“贝叶斯定理是一个数学定理,它解释了为什么如果世界上所有的汽车都是蓝色的,那么我的车一定是蓝色的,但仅仅因为我的车是蓝色的,并不意味着世界上所有的汽车都是蓝色的。
在数学术语中,给定事件“A”和“B”,给定事件“B”发生,事件“A”发生的概率如下:
![]()
鉴于事件“A”已发生,事件“B”发生的概率如下:
![]()
链接第一个表达式和最后一个表达式的公式如下:
![]()
明白了?伟大。现在,假设你有你的神经网络模型。这个神经网络只不过是一组参数,用于将给定的输入转换为所需的输出。
前馈神经网络(最简单的深度学习结构)通过将输入乘以参数矩阵来处理您的输入。然后,将非线性激活函数(这是神经网络的真正功能)应用于该矩阵乘法的结果。结果是下一层的输入,其中应用了相同的过程。
现在,我们将模型的参数集称为 w。现在我们可以问自己这个棘手的问题。
假设我有一个数据集 D,它是一组输入x_i和输出y_i对,例如,动物的第 i 张图像和第 i 张标签(猫或狗):
![]()
给定某个数据集 D,拥有一组参数的概率是多少?
您可能需要阅读这个问题 3 或 4 遍才能掌握它,但这个想法就在那里。如果输入和输出之间有一定的映射,则在极端确定性情况下,只有一组参数能够处理输入并带来所需的输出。以概率方式,将存在一组参数,该参数集比另一个参数更可能。
所以我们感兴趣的是数量。
![]()
现在,有三件事很酷:
- 当您考虑给定该分布的平均值时,您仍然可以将其视为标准神经网络模型。例如:

方程的左手表示计算出的平均输出,右手表示所有可能的参数结果集的平均值 (N),概率分布为每个结果提供权重。
2. 虽然 p(w|D)显然是一个谜,p(D|w)是我们总是可以研究的东西。如果我们将上面的等式用于一个巨大的 N,则不需要机器学习。你可以简单地说:“在给定某个神经网络的情况下尝试所有可能的模型,并使用上面的等式权衡所有可能的结果”
3. 当我们得到 p 时,我们得到的不仅仅是一个机器学习模型;我们实际上得到了无限的机器学习模型。这意味着我们可以从您的预测中提取一些不确定性边界和统计信息。结果不仅是“10.23”,而且更像是“10.23,可能的误差为 0.50”。
我希望我炒作了你。让我们进入下一章
四、一些数学
我不希望这篇文章是闲聊,但我不希望它成为痛苦。如果您了解贝叶斯神经网络的概念,或者您已经知道它们背后的数学原理,请随时跳过本章。如果你想有一个参考,一个好的参考是以下。(动手贝叶斯神经网络 — 深度学习用户教程)
现在这一切看起来很酷,但我认为,如果你是一个机器学习用户,你就会有这样的想法:
“我怎么能优化这么奇怪的生物呢?”
简短的回答是,“通过最大化:
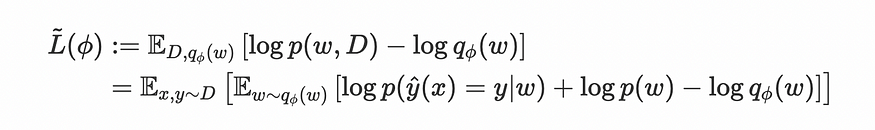
但我不认为这是不言自明的。
在这种情况下,优化原则是找到分布 p(w|我们将这个分布称为 q,我们想要一个两个分布函数之间距离的度量。
我们将使用的指标称为 Kullback-Leibler 背离

关于它的一些有趣的事实:
- 对于两个相等的分布,它是 0
- 如果两个分布的分母趋于零,而分子仍非零,则它是无穷大的
- 它是不对称的。
现在,您在上面看到的损失函数是 Kullback-Leibler 散度的代理量,它被称为证据下界 (ELBO)。
权重 q 的分布被认为是具有均值 mu 和方差 sigma2 的正态分布:
![]()
因此,优化是关于确定该分布的最佳 mu 和 sigma 值。
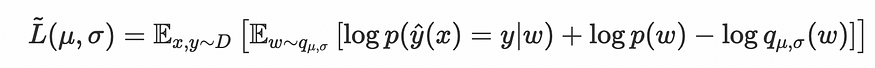
在实际的 PyTorch 实现中,分布均值和目标之间的 MSE 也被添加到我们的 L (mu, sigma) 中。
五、pyt(orch)hon 实现
借助名为 torchbnn 的库,使用 PyTorch 在 Python 中实现贝叶斯神经网络非常简单。
安装它非常容易:
pip install torchbnn正如我们将看到的,我们将构建一些与标准 Tor 神经网络非常相似的东西:
model = nn.Sequential(bnn.BayesLinear(prior_mu=0, prior_sigma=0.1, in_features=1, out_features=1000),nn.ReLU(),bnn.BayesLinear(prior_mu=0, prior_sigma=0.1, in_features=1000, out_features=1),
)实际上,有一个库可以将您的火炬模型转换为其贝叶斯代理项:
transform_model(model, nn.Conv2d, bnn.BayesConv2d, args={"prior_mu":0, "prior_sigma":0.1, "in_channels" : ".in_channels","out_channels" : ".out_channels", "kernel_size" : ".kernel_size","stride" : ".stride", "padding" : ".padding", "bias":".bias"}, attrs={"weight_mu" : ".weight"})但是,让我们做一个动手的详细示例:
六、动手回归任务
首先要做的是导入一些库:
import numpy as np
from sklearn import datasets
import torch
import torch.nn as nn
import torch.optim as optim
import torchbnn as bnn
import matplotlib.pyplot as plt之后,我们将制作非常简单的二维数据集:
x = torch.linspace(-2, 2, 500)
y = x.pow(5) -10* x.pow(1) + 2*torch.rand(x.size())
x = torch.unsqueeze(x, dim=1)
y = torch.unsqueeze(y, dim=1)plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()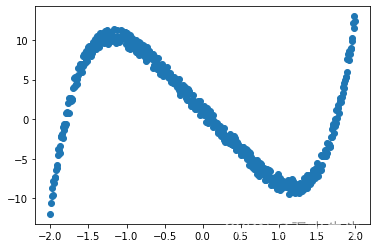
因此,给定我们的 1D 输入 x(范围从 -2 到 2),我们希望找到我们的 y。
def clean_target(x):return x.pow(5) -10* x.pow(1)+1
def target(x):return x.pow(5) -10* x.pow(1) + 2*torch.rand(x.size())Clean_target 是我们的地面实况生成器,Target 是嘈杂的数据生成器。
现在我们将定义贝叶斯前馈神经网络:
model = nn.Sequential(bnn.BayesLinear(prior_mu=0, prior_sigma=0.1, in_features=1, out_features=1000),nn.ReLU(),bnn.BayesLinear(prior_mu=0, prior_sigma=0.1, in_features=1000, out_features=1),
)正如我们所看到的,它是一个具有贝叶斯层的两层前馈神经网络。这将使我们能够获得概率输出。
现在我们将定义我们的 MSE 损失和剩余的 Kullback-Leibler 背离:
mse_loss = nn.MSELoss()
kl_loss = bnn.BKLLoss(reduction='mean', last_layer_only=False)
kl_weight = 0.01optimizer = optim.Adam(model.parameters(), lr=0.01)这两个损失都将用于我们的优化步骤:
for step in range(2000):pre = model(x)mse = mse_loss(pre, y)kl = kl_loss(model)cost = mse + kl_weight*kloptimizer.zero_grad()cost.backward()optimizer.step()print('- MSE : %2.2f, KL : %2.2f' % (mse.item(), kl.item()))已经使用了 2000 个 epoch。
让我们定义我们的测试集:
x_test = torch.linspace(-2, 2, 300)
y_test = target(x_test)x_test = torch.unsqueeze(x_test, dim=1)
y_test = torch.unsqueeze(y_test, dim=1)现在,模型类的结果是概率性的。这意味着,如果我们运行模型 10,000 次,我们将得到 10,000 个略有不同的值。对于从 -2 到 2 的每个数据点,我们将得到平均值和标准差,
models_result = np.array([model(x_test).data.numpy() for k in range(10000)])
models_result = models_result[:,:,0]
models_result = models_result.T
mean_values = np.array([models_result[i].mean() for i in range(len(models_result))])
std_values = np.array([models_result[i].std() for i in range(len(models_result))])我们将绘制我们的置信区间。
plt.figure(figsize=(10,8))
plt.plot(x_test.data.numpy(),mean_values,color='navy',lw=3,label='Predicted Mean Model')
plt.fill_between(x_test.data.numpy().T[0],mean_values-3.0*std_values,mean_values+3.0*std_values,alpha=0.2,color='navy',label='99.7% confidence interval')
#plt.plot(x_test.data.numpy(),mean_values,color='darkorange')
plt.plot(x_test.data.numpy(),y_test.data.numpy(),'.',color='darkorange',markersize=4,label='Test set')
plt.plot(x_test.data.numpy(),clean_target(x_test).data.numpy(),color='green',markersize=4,label='Target function')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')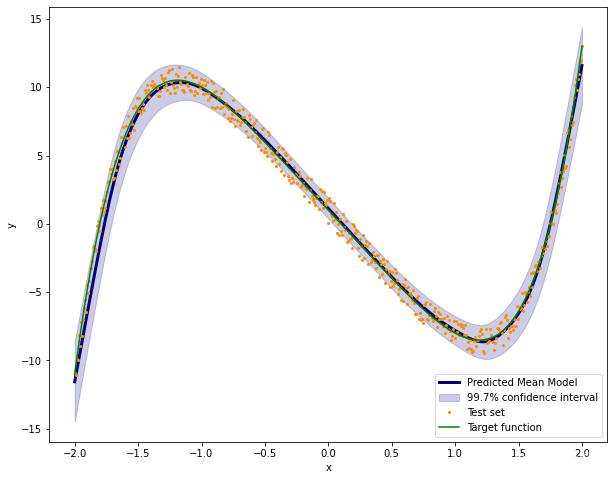
七、参考地址
A. 在 LinkedIn
B. 订阅我的时事通讯。
From Theory to Practice with Bayesian Neural Network, Using Python | by Piero Paialunga | Towards Data Science
相关文章:

使用 Python 使用贝叶斯神经网络从理论到实践
一、说明 在本文中,我们了解了如何构建一个机器学习模型,该模型结合了神经网络的强大功能,并且仍然保持概率方法进行预测。为了做到这一点,我们可以构建所谓的贝叶斯神经网络。 这个想法不是优化神经网络的损失࿰…...
Linux 中的网站服务管理
目录 1.安装服务 2.启动服务 3.停止服务 4.重启服务 5.开机自启 6.案例 1.安装服务 网址服务程序 yum insatll httpd -y 查看所有服务 systemctl list-unit-files 2.启动服务 systemctl start httpd 查看服务进程,确认是否启动 ps -ef|grep httpd 3.停止…...
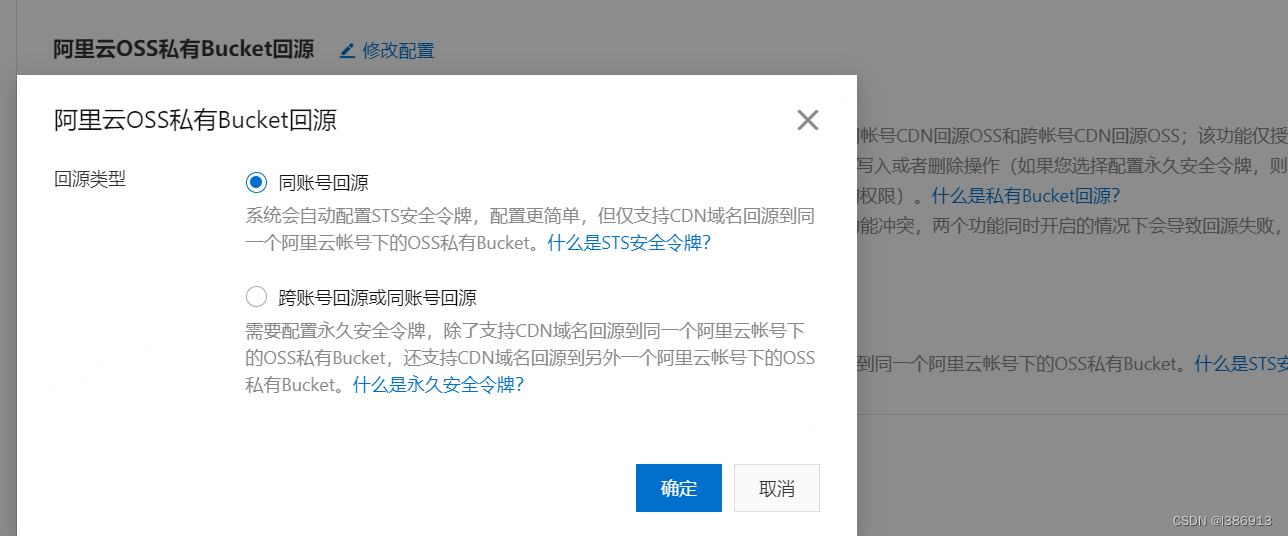
阿里云cdn设置相同的域名路径访问不同的oss目录
1.设置回源配置,添加回源URL改写 2.设置跨域,cdn的跨域优先oss 3.回源设置...
工程中提示词的开发优化基础概念学习总结)
提示(Prompt)工程中提示词的开发优化基础概念学习总结
本文对学习过程进行总结,仅对基本思路进行说明,结果在不同的模型上会有差异。 提示与提示工程 提示:指的是向大语言模型输入的特定短语或文本,用于引导模型产生特定的输出,以便模型能够生成符合用户需求的回应。 提示…...

C#基础——语法学习
C#的基本语法 在介绍基本语法之前我们先来大概讲一下创建好的这些文件都是做什么的 .sln文件:将项目和解决方案项结合到一起 .vs文件夹:用来存储当前解决方案中关于用户的设置和自定义项,比如断点,主题等。(一般都将其…...
vue-实现高德地图-省级行政区地块显示+悬浮显示+标签显示
<template><div><div id"container" /><div click"showFn">显示</div><div click"removeFn">移除</div></div> </template><script> import AMapLoader from amap/amap-jsapi-load…...

flutter ‘Gradle Libs‘ was added by build file ‘app/build.gradle‘
相关问题解释文章 How to prefer settings.gradle repositories over build.gradle repositoriesMode 解释 问题描述 此问题是,直接创建的flutter项目,需要配置其他的maven仓库地址,和第三方module,结果始终都是无法成功 错误…...

Java中的链式编程风格与应用案例
引言 链式编程是一种在编程中经常使用的风格,它可以使代码更加简洁、易读和易于维护。在Java中,链式编程可以通过方法链的方式来实现。本文将介绍Java中的链式编程风格,并通过几个应用案例来说明其实际应用。 一、链式编程的概念与特点 链式…...
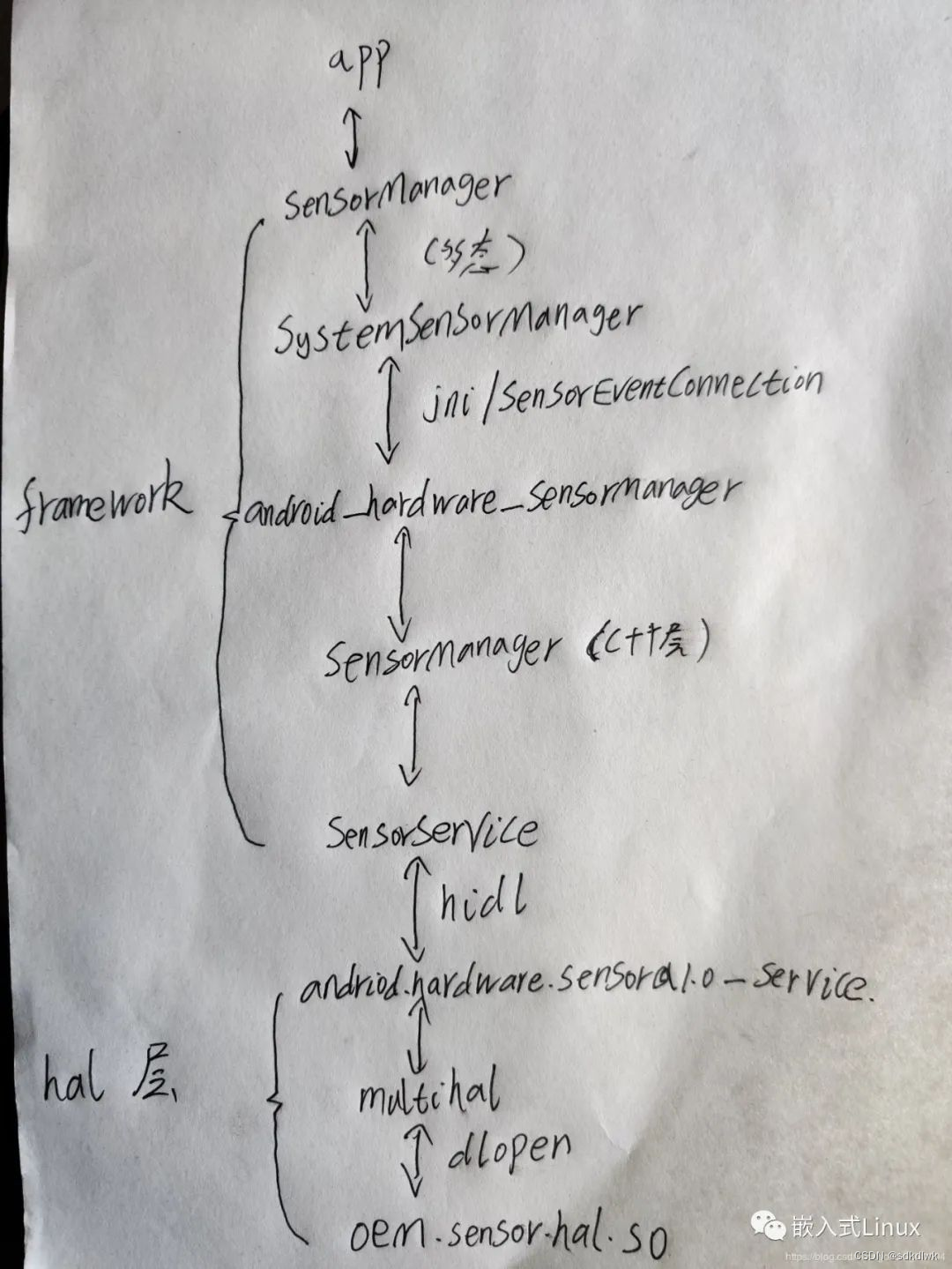
MTK Android P Sensor架构(一)
需求场景: 本来如果只是给传感器写个驱动并提供能读取温湿度数据的节点,是一件比较轻松的事情,但是最近上层应用的同事要求我们按照安卓标准的流程来,这样他们就能通过注册一个服务直接读取传感器事件数据了。这样做的好处就是第…...

低代码开发与传统软件开发:未来趋势与竞争格局
近年来,低代码开发平台的快速发展引起了各行各业的广泛关注。低代码开发平台简化了软件开发的复杂性,提供了更快速、更灵活的开发方式。于是,许多人开始产生一个疑问:未来低代码开发是否会取代传统软件开发?今天这篇文…...

leetcode 股票问题全序列
1 只允许一次交易,121题,买卖股票的最佳时机 class Solution {/*给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票…...

SpringBoot中日志的使用log4j2
SpringBoot中日志的使用log4j2 1、log4j2介绍 Apache Log4j2 是对 Log4j 的升级,它比其前身 Log4j 1.x 提供了重大改进,并提供了 Logback 中可用的许多改 进,同时修复了 Logback 架构中的一些问题,主要有: 异常处理…...
机械设备企业网站建设的效果如何
机械设备涵盖的类目比较广,其市场需求也是稳增不减,也因此无论大小企业都有增长的机会,当然这也需要靠谱的工具及正确的决策。 对机械设备企业来说,产品品质自然是首位,而向外打造品牌、扩展信息及拓客转化自然也是非…...

设计模式之结构型设计模式(二):工厂模式 抽象工厂模式 建造者模式
工厂模式 Factory 1、什么是工厂模式 工厂模式旨在提供一种统一的接口来创建对象,而将具体的对象实例化的过程延迟到子类或者具体实现中。有助于降低客户端代码与被创建对象之间的耦合度,提高代码的灵活性和可维护性。 定义了一个创建对象的接口&…...

算法模板之单链表图文讲解
🌈个人主页:聆风吟 🔥系列专栏:算法模板、数据结构 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️使用数组模拟单链表讲解1.1 🔔为什么我们要使用数组去模拟单链表…...

【强化学习-读书笔记】表格型问题的 Model-Free 方法
参考 Reinforcement Learning, Second Edition An Introduction By Richard S. Sutton and Andrew G. Barto无模型方法 在前面的文章中,我们介绍的是有模型方法(Model-Based)。在强化学习中,"Model"可以理解为算法…...

【手撕算法系列】k-means
k-means k-means算法介绍 k-means算法介绍 K-means算法是一种用于聚类的迭代算法,它将数据集划分为K个簇,其中每个数据点属于与其最近的簇的中心。这个算法的目标是最小化簇内的平方和误差(簇内数据点与簇中心的距离的平方和)。 …...

D33|动态规划!启程!
1.动态规划五部曲: 1)确定dp数组(dp table)以及下标的含义 2)确定递推公式 3)dp数组如何初始化 4)确定遍历顺序 5)举例推导dp数组 2.动态规划应该如何debug 找问题的最好方式就是把…...
C语言----文件操作(二)
在上一篇文章中我们简单介绍了在C语言中文件是什么以及文件的打开和关闭操作,在实际工作中,我们不仅仅是要打开和关闭文件,二是需要对文件进行增删改写。本文将详细介绍如果对文件进行安全读写。 一,以字符形式读写文件ÿ…...

oracle 10046事件跟踪
10046事件是一个很好的排查sql语句执行缓慢的内部事件,具体设置方式如下: 根据10046事件跟踪SQL语句 1、 alter session set events 10046 trace name context forever,level 12; 2、执行SQL语句 3、关闭10046事件 alter session set events 10046 trace…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
