【单调栈 】LeetCode321:拼接最大数
作者推荐
【动态规划】【广度优先搜索】LeetCode:2617 网格图中最少访问的格子数
本文涉及的知识点
单调栈
题目
给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k (k <= m + n) 个数字拼接成一个新的数,要求从同一个数组中取出的数字保持其在原数组中的相对顺序。
求满足该条件的最大数。结果返回一个表示该最大数的长度为 k 的数组。
说明: 请尽可能地优化你算法的时间和空间复杂度。
示例 1:
输入:
nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
输出:
[9, 8, 6, 5, 3]
示例 2:
输入:
nums1 = [6, 7]
nums2 = [6, 0, 4]
k = 5
输出:
[6, 7, 6, 0, 4]
示例 3:
输入:
nums1 = [3, 9]
nums2 = [8, 9]
k = 3
输出:
[9, 8, 9]
单调栈
时间复杂度: O(k(m+n+max(n,m)*max(n,m)))。枚举m和n,时间复杂度O(k)。对于任意m,n组合,处理分如下四步:一,计算nums1的长度为m的最大字典序子序列v1。二,计算nums2的长度为n的最大字典序子序列v2。三,合并v1和v2到cur。四,比较cur和vRet大小。
对应任意m,n只需要考虑最大字典序
假定最终结果中来自于nums1的元素组成的子序列不是最大字典序,换成最大字典序列。也符合题意,字典序不变或变大。
长度为len的最大字典序
vVet[0,i]记录长度i+1的最大字典序子序列。可以把vRet看成队列,当新元素大于队尾元素时,替换队尾元素,会形成新的最大子序列。可以一直替换指导队尾元素大于等于当前元素或队列为空。这样的问题是vRet的长度可能不为空,解决方法:
| 如果出队后,剩余数字全部入队,都无法让vRet的长度大于等于k | 则不出队 |
| 如果vRet.size()>=k | 则不入队 |
合并v1v2
我们把v1,v2看成队列,每次只能取队首。每次取两个队首的较大值,如果相等,则:
假定v1和v2有相同的前缀vPre,其长度为len,假定v1的vPre后面是c,假定v2和vPre后面的d。选择v1或v2,前len个字符都可以相同。选择v1,第len+1个字符可以是c,不能是d。选择v2,第len+1个字符是d,不能是c。显然c大,选择v1;d大,选择v2。我们来考虑特殊情况:
| c和d不存在 | v1和v2完全相同,选v1和v2的效果一样 |
| c存在,d不存在 | 为了len+1能选择c,选择v1 |
| d存在,c不存在 | 为了len+1能选择d,选择v2 |
综上所述:就是选择字典序大的,可用lexicographical_compare 简化代码。
代码
核心代码
class Solution {
public:vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {vector<int> vRet(k);for (int len1 = 0; len1 <= min((int)nums1.size(), k); len1++){const int len2 = k - len1;if (len2 > nums2.size()){continue;}if (len2 < 0){break;}vector<int> v1 = TopMax(nums1, len1);vector<int> v2 = TopMax(nums2, len2);vector<int> cur;int i1 = 0, i2 = 0;while ((i1 < v1.size()) && (i2 < v2.size())){auto Cmp = [&v1,&v2](int i1,int i2){ while((i1<v1.size())&&(i2 < v2.size())){const int iCmp = v1[i1] - v2[i2];if (iCmp > 0 ){return true;;}else if (iCmp < 0){return false;}i1++;i2++;} return i1 < v1.size();};if (Cmp(i1,i2)){cur.emplace_back(v1[i1++]);}else{cur.emplace_back(v2[i2++]);}}cur.insert(cur.end(), v1.begin() + i1, v1.end());cur.insert(cur.end(), v2.begin() + i2, v2.end());vRet = max(cur, vRet);}return vRet;}vector<int> TopMax(const vector<int>& nums, int k){vector<int> ret;for (int i = 0; i < nums.size(); i++){while (ret.size() && (ret.back() < nums[i]) && (ret.size() + nums.size() - i > k)){ret.pop_back();}if (ret.size() < k){ret.emplace_back(nums[i]);}}return ret;}
};
测试用例
template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){assert(v1[i] == v2[i]);}
}template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}int main()
{vector<int> nums1, nums2;int k;{Solution slu; nums1 = { 3, 4, 6, 5 };nums2 = { 9, 1, 2, 5, 8, 3 };k = 5;auto res = slu.maxNumber(nums1, nums2, k);Assert(vector<int>{9, 8, 6, 5, 3}, res);}{Solution slu;nums1 = { 6, 7 };nums2 = { 6, 0, 4 };k = 5;auto res = slu.maxNumber(nums1, nums2, k);Assert(vector<int>{6, 7, 6, 0, 4}, res);}{Solution slu;nums1 = { 3, 9 };nums2 = { 8,9 };k = 3;auto res = slu.maxNumber(nums1, nums2, k);Assert(vector<int>{9, 8, 9}, res);}
}
简化后的代码
class Solution {
public:vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {vector<int> vRet(k);for (int len1 = 0; len1 <= min((int)nums1.size(), k); len1++){const int len2 = k - len1;if (len2 > nums2.size()){continue;}if (len2 < 0){break;}vector<int> v1 = TopMax(nums1, len1);vector<int> v2 = TopMax(nums2, len2);vector<int> cur;auto it1 = v1.begin();auto it2 = v2.begin();for (;(it1 != v1.end()) && (it2 != v2.end());){ if (lexicographical_compare(it1,v1.end(),it2,v2.end())){cur.emplace_back(*it2++);}else{cur.emplace_back(*it1++);} }cur.insert(cur.end(), it1, v1.end());cur.insert(cur.end(), it2, v2.end());vRet = max(cur, vRet);}return vRet;}vector<int> TopMax(const vector<int>& nums, int k){vector<int> ret;for (int i = 0; i < nums.size(); i++){while (ret.size() && (ret.back() < nums[i]) && (ret.size() + nums.size() - i > k)){ret.pop_back();}if (ret.size() < k){ret.emplace_back(nums[i]);}}return ret;}
};
2023年3月
class Solution {
public:
vector maxNumber(vector& nums1, vector& nums2, int k) {
vector vRet;
for (int iLeft = 0; iLeft <= k; iLeft++)
{
const vector v1 = maxNumber(nums1, iLeft);
const vector v2 = maxNumber(nums2, k - iLeft);
if (v1.size() + v2.size() != k)
{
continue;
}
vector nums;
auto it1 = v1.begin();
auto it2 = v2.begin();
while ((it1 != v1.end() ) && (it2 != v2.end() ))
{
if (*it1 > *it2 )
{
nums.push_back(*it1);
it1++;
}
else if(*it1 < *it2)
{
nums.push_back(*it2);
it2++;
}
else
{
if (Less(it1, v1.end(), it2, v2.end()))
{
nums.push_back(*it2);
it2++;
}
else
{
nums.push_back(*it1);
it1++;
}
}
}
std::copy(it1, v1.end(), std::back_inserter(nums));
std::copy(it2, v2.end(), std::back_inserter(nums));
if ((vRet.size() == 0) || Less(vRet,nums))
{
vRet.swap(nums);
}
}
return vRet;
}
template
bool Less(IT itBegin1, IT itEnd1, IT itBegin2, IT itEnd2)
{
while ((itBegin1 != itEnd1) && (itBegin2 != itEnd2))
{
if (*itBegin1 < *itBegin2)
{
return true;
}
else if (*itBegin1 > *itBegin2)
{
return false;
}
itBegin1++;
itBegin2++;
}
return itBegin1 == itEnd1;
}
bool Less(const vector& v1, const vector& v2)
{
for (int i = 0; i < v1.size(); i++)
{
if (v1[i] < v2[i])
{
return true;
}
else if (v1[i] > v2[i])
{
return false;
}
}
return false;
}
vector maxNumber(const vector& nums, int k)
{
vector ret;
for (int i = 0; i < nums.size(); i++)
{
const int& n = nums[i];
while (ret.size() && (n > ret.back()) && ((ret.size() + nums.size() - i - 1) >= k))
{
ret.pop_back();
}
if (ret.size() < k)
{
ret.push_back(n);
}
}
return ret;
}
};
2023 年8月
template<class T = int,class _Pr = std::less >
class CTopK
{
public:
CTopK(int k):m_iMinNum(k)
{
}
void Do(vector& m_v,T* begin, int num)
{
for (; num ; begin++,num–)
{
while (m_v.size() && _Pr()( *begin, m_v.back()) && (m_iMinNum - m_v.size()+1 <= num))
{
m_v.pop_back();
}
if (m_v.size() < m_iMinNum)
{
m_v.push_back(*begin);
}
}
}
protected:
const int m_iMinNum;
};
class Solution {
public:
vector maxNumber(vector& nums1, vector& nums2, int k) {
CTopK<int,std::greater> tok(k);
vector<vector> vNums1(k + 1), vNums2(k + 1);
tok.Do(vNums1[k], nums1.data(), nums1.size());
tok.Do(vNums2[k], nums2.data(), nums2.size());
for (int i = k - 1; i >0; i–)
{
CTopK<int, std::greater> tok(i);
tok.Do(vNums1[i], vNums1[i + 1].data(), vNums1[i + 1].size());
tok.Do(vNums2[i], vNums2[i + 1].data(), vNums2[i + 1].size());
}
vector vRet(k);
for (int i = max(0,k-(int)nums2.size()); i <= min(k,(int)nums1.size()); i++)
{
const auto& v1 = vNums1[i];
const auto& v2 = vNums2[k - i];
vector cur;
auto it = v1.begin();
auto ij = v2.begin();
while ((it != v1.end()) || (ij != v2.end()))
{
bool b = lexicographical_compare(it, v1.end(), ij, v2.end());
if (b)
{
cur.emplace_back((ij++));
}
else
{
cur.emplace_back((it++));
}
}
if (cur > vRet)
{
vRet.swap(cur);
}
}
return vRet;
}
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【单调栈 】LeetCode321:拼接最大数
作者推荐 【动态规划】【广度优先搜索】LeetCode:2617 网格图中最少访问的格子数 本文涉及的知识点 单调栈 题目 给定长度分别为 m 和 n 的两个数组,其元素由 0-9 构成,表示两个自然数各位上的数字。现在从这两个数组中选出 k (k < m n) 个数字…...

TikTok与虚拟现实的完美交融:全新娱乐时代的开启
TikTok,这个风靡全球的短视频平台,与虚拟现实(VR)技术的深度结合,为用户呈现了一场全新的娱乐盛宴。虚拟现实技术为TikTok带来了更丰富、更沉浸的用户体验,标志着全新娱乐时代的开启。本文将深入探讨TikTok…...

PXI/PCIe/VPX机箱 ARM|x86 + FPGA测试测量板卡解决方案
PXI便携式测控系统是一种基于PXI总线的便携式测试测控系统,它填补了现有台式及机架式仪器在外场测控和便携测控应用上的空白,在军工国防、航空航天、兵器电子、船舶舰载等各个领域的外场测控场合和科学试验研究场合都有广泛的应用。由于PXI便携式测控系统…...

ES6 面试题 | 12.精选 ES6 面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

【linux】Debian不能运行sudo的解决
一、问题: sudo: 没有找到有效的 sudoers 资源,退出 sudo: 初始化审计插件 sudoers_audit 出错 二、可用的方法: 出现 "sudo: 没有找到有效的 sudoers 资源,退出" 和 "sudo: 初始化审计插件 sudoers_audit 出错&q…...

讲解ThinkPHP的链式操作
数据库提供的链式操作方法,可以有效的提高数据存取的代码清晰度和开发效率,并且支持所有的CURD操作。 使用也比较简单,假如我们现在要查询一个User表的满足状态为1的前10条记录,并希望按照用户的创建时间排序 Db::table(think_u…...
Java技术栈 —— 微服务框架Spring Cloud —— Ruoyi-Cloud 学习(二)
RuoYi项目开发过程 一、登录功能(鉴权模块)1.1 后端部分1.1.1 什么是JWT?1.1.2 什么是Base64?为什么需要它?1.1.3 SpringBoot注解解析1.1.4 依赖注入和控制反转1.1.5 什么是Restful?1.1.6 Log4j 2、Logpack、SLF4j日志框架1.1.7 如何将项目打包成指定bytecode字节…...
?)
如何进行软件测试和测试驱动开发(TDD)?
1. 软件测试概述 1.1 什么是软件测试? 软件测试是一种评估系统的过程,目的是发现潜在的错误或缺陷。通过对软件进行测试,开发者和测试人员可以确定软件是否符合预期的需求、功能是否正常运行,以及系统是否足够稳定和可靠。 1.2…...
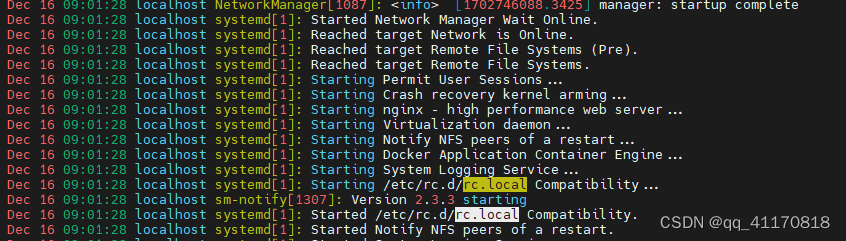
linux 开机启动流程
1.打开电源 2.BIOS 有时间和启动方式 3.启动Systemd 其pid为1 4.挂载引导分区 /boot 5.启动各种服务 如rc.local...
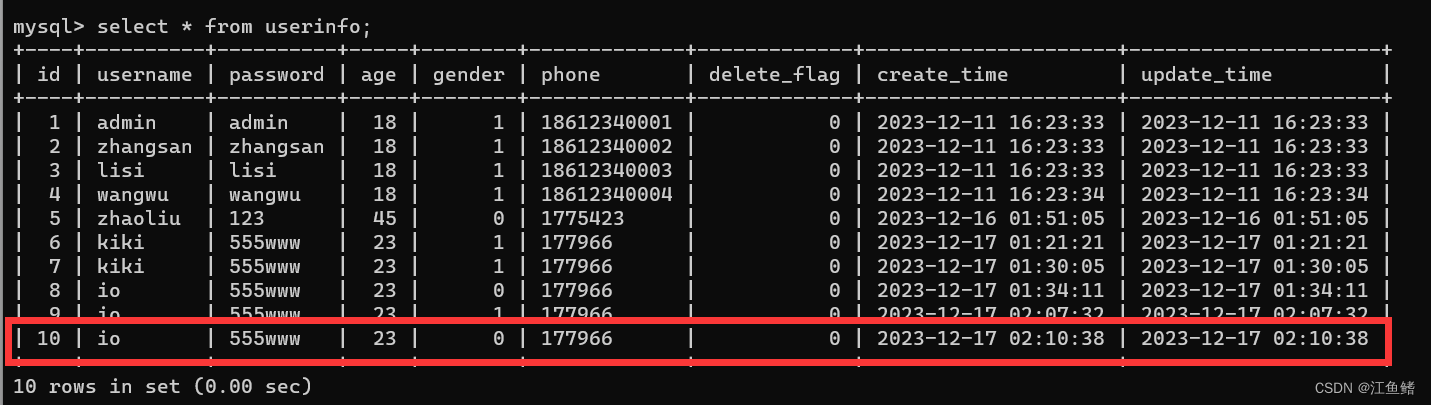
Mybatis 动态SQL的插入操作
需求 : 根据用户的输入情况进行插入 动态SQL:根据需求动态拼接SQL 用户往表中插入数据,有的数据可能不想插入,比如不想让别人知道自己的性别,性别就为空 insert into userinfo(username,password,age,gender,phone) values(?,?,?,?,?); insert into userinfo(username,…...

共建开源新里程:北京航空航天大学OpenHarmony技术俱乐部正式揭牌成立
12月11日,由OpenAtom OpenHarmony(以下简称“OpenHarmony”)项目群技术指导委员会(以下简称“TSC”)和北京航空航天大学共同举办的“OpenHarmony软件工程研讨会暨北京航空航天大学OpenHarmony技术俱乐部成立仪式”在京圆满落幕。 现场大合影 活动当天,多位重量级嘉宾出席了此次…...

企业微信机器人发送文本、图片、文件、markdown、图文信息
import requests import base64 import hashlib import json # 机器人地址的key值 key"811a1652-60e8-4f51-a1d9-231783399ad2" def path2base64(path):"""文件转换为base64:param path: 文件路径:return:"""with open(path, "rb…...

智能优化算法应用:基于天牛须算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于天牛须算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于天牛须算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.天牛须算法4.实验参数设定5.算法结果6.参考文…...

【Hive】【Hadoop】工作中常操作的笔记-随时添加
文章目录 1、Hive 复制一个表:2、字段级操作3、hdfs 文件统计 1、Hive 复制一个表: 直接Copy文件 create table new_table like table_name;hdfs dfs -get /apps/hive/warehouse/ods.db/table_nameload data local inpath /路径 into table new_table;修复表: m…...

DIY电脑装机机箱风扇安装方法
作为第一次自己diy一台电脑主机的我,在经历了众多的坑中今天来说一下如何安装机箱风扇的问题 一、风扇的数量 1、i3 xx50显卡 就用一个cpu散热风扇即可 2、i5 xx60 一个cpu散热风扇 一个风扇即可 3、i7 xx70 一个cpu散热 4个风扇即可 4、i9 xx80 就需要7个以…...

基础算法(4):排序(4)冒泡排序
1.冒泡排序(BubbleSort)实现 算法步骤:比较相邻的元素。如果第一个比第二个大,就交换。 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。 这步做完后,最后的元素会是最大的数。 针对所有的元素重复以上的步骤&#…...

鸿蒙开发之网络请求
//需要导入http头文件 import http from ohos.net.http//请求地址url: string http://apis.juhe.cn/simpleWeather/queryText(this.message).maxFontSize(50).minFontSize(10).fontWeight(FontWeight.Bold).onClick(() > {console.log(请求开始)let req http.createHttp()…...
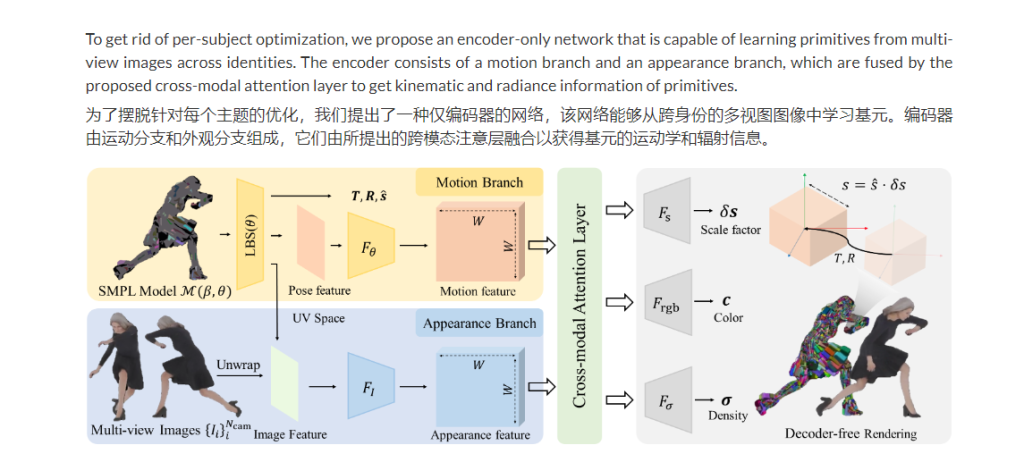
PrimDiffusion:3D 人类生成的体积基元扩散模型NeurIPS 2023
NeurIPS2023 ,这是一种用于 3D 人体生成的体积基元扩散模型,可通过离体拓扑实现明确的姿势、视图和形状控制。 PrimDiffusion 对一组紧凑地代表 3D 人体的基元执行扩散和去噪过程。这种生成建模可以实现明确的姿势、视图和形状控制,并能够在…...
时序预测 | Python实现LSTM-Attention-XGBoost组合模型电力需求预测
时序预测 | Python实现LSTM-Attention-XGBoost组合模型电力需求预测 目录 时序预测 | Python实现LSTM-Attention-XGBoost组合模型电力需求预测预测效果基本描述程序设计参考资料预测效果 基本描述 该数据集因其每小时的用电量数据以及 TSO 对消耗和定价的相应预测而值得注意,从…...
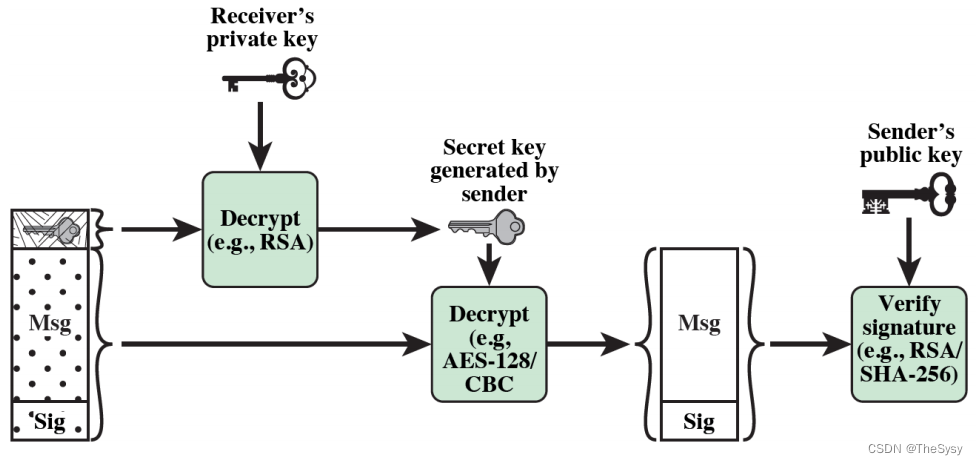
【网络安全技术】电子邮件安全PGP,SMIME
一、PGP(Pretty Good Privacy) PGP是一种邮件加密手段,他在发邮件一方加密,然后发给发送方邮件服务器,发送方邮件服务器再发送给接收方邮件服务器,然后接收方再从接收方邮件服务器pop出来,这整…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
