容斥原理的并
文章目录
- 简介
- AcWing 890. 能被整除的数
- 思路解析
- CODE
简介
推荐题解:https://www.acwing.com/solution/content/126553/
画了图,清晰易懂,懒得打字了。
总之就是以下公式: S = S 1 + S 2 + S 3 − S 1 ∩ S 2 − S 1 ∩ S 3 − S 2 ∩ S 3 + S 1 ∩ S 2 ∩ S 3 \begin{align*} S = & S_1 + S_2 + S_3 \\ & - S_1 \cap S_2 - S_1 \cap S_3 - S_2 \cap S_3 \\ & + S_1 \cap S_2 \cap S_3 \end{align*} S=S1+S2+S3−S1∩S2−S1∩S3−S2∩S3+S1∩S2∩S3
我们可以把这个式子推导到 n n n 维,奇加偶减。
AcWing 890. 能被整除的数
题目链接:https://www.acwing.com/activity/content/problem/content/960/

思路解析
筛出一个数的倍数,两个数的倍数 … n n n 个数的倍数,这就抽象成了 n n n 个集合的问题了。
那么如何表示选取哪几个集合(质数)呢?
- 从 1 1 1 开始枚举到 n n n,将每个数看成二进制形式,如果说第 k k k 位是 1 1 1,那么就代表选第 k k k 个集合,反之不选。
如何知道被整除的数的个数?公式: n / p n / p n/p 下取整即可。
最后判断是奇数个还是偶数个,这个判断利用了二进制的一个性质:除了 2 0 2^0 20,其他所有位的和都是 2 2 2 的整数倍,所以说看是否为奇数就看它二进制最后一位是否为 1 1 1。
CODE
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;typedef long long ll; // 定义长整型别名为llconst int N = 20; // 定义常量N为20
int n, m; // 定义整型变量n和m
int p[N]; // 定义整型数组p,大小为Nint main(){scanf("%d%d", &n, &m); // 从输入中读取两个整数n和mfor(int i = 0; i < m; ++i) scanf("%d", &p[i]); // 从输入中读取m个整数到数组p中int res = 0; // 初始化结果为0for(int i = 1; i < (1 << m); ++i){ // 遍历所有的子集int s = 0, t = 1; // 初始化s和tfor(int j = 0; j < m; ++j){ // 遍历每一位if(i >> j & 1){ // 如果第j位为1if((ll)t * p[j] > n){ // 如果t乘以p[j]大于nt = -1; // 将t设置为-1break; // 跳出循环}t *= p[j]; // 更新ts++; // 增加s}}if(t == -1) continue; // 如果t为-1,跳过当前循环if(s & 1) res += n / t; // 如果s为奇数,增加n/t到reselse res -= n / t; // 否则,从res中减去n/t}cout << res << endl; // 输出结果
}相关文章:

容斥原理的并
文章目录 简介AcWing 890. 能被整除的数思路解析CODE 简介 推荐题解:https://www.acwing.com/solution/content/126553/ 画了图,清晰易懂,懒得打字了。 总之就是以下公式: S S 1 S 2 S 3 − S 1 ∩ S 2 − S 1 ∩ S 3 − S 2 …...
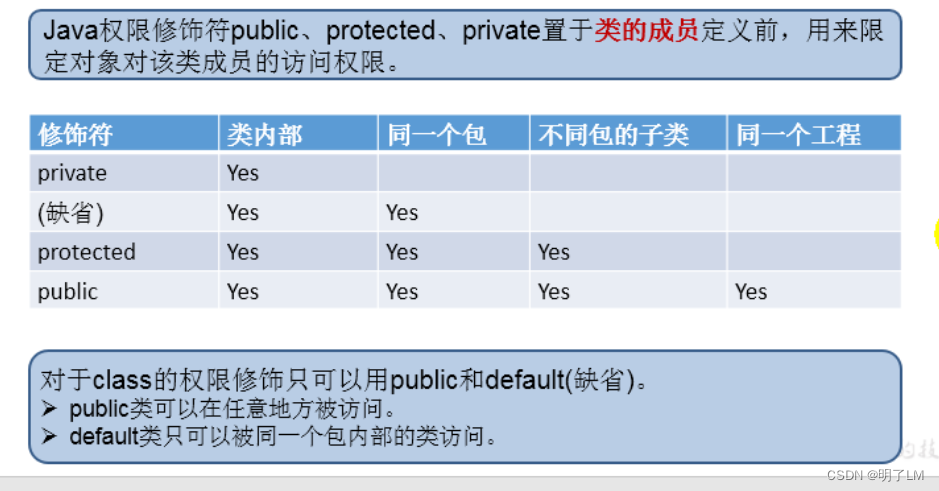
JavaSE第7篇:封装
文章目录 一、封装1、好处:2、使用 二、四种权限修饰符三、构造器1、作用2、说明3、属性赋值的过程 一、封装 封装就是将类的属性私有化,提供公有的方法访问私有属性 不对外暴露打的私有的方法 单例模式 1、好处: 1.只能通过规定的方法来访问数据 2.隐藏类的实例细节,方便…...

mysql数据库相关知识【MYSQL】
mysql数据库相关知识【MYSQL】 一. 库1.1 登录数据库管理系统1.2 什么是数据库1.2.1 mysqld与mysql 1.3 编码集和校验集1.3.1 什么是编码集和校验集1.3.2 查看库对应的编码集和校验集1.3.3 用指定的编码集和校验集 1.4 库的操作 一. 库 1.1 登录数据库管理系统 这个算是第一个…...
android studio 创建按钮项目
1)、新建一个empty activity项目,切换到project视图: 2)、修改app\src\main\res\layout\activity_main.xml文件,修改后如下: <?xml version"1.0" encoding"utf-8"?> <andr…...
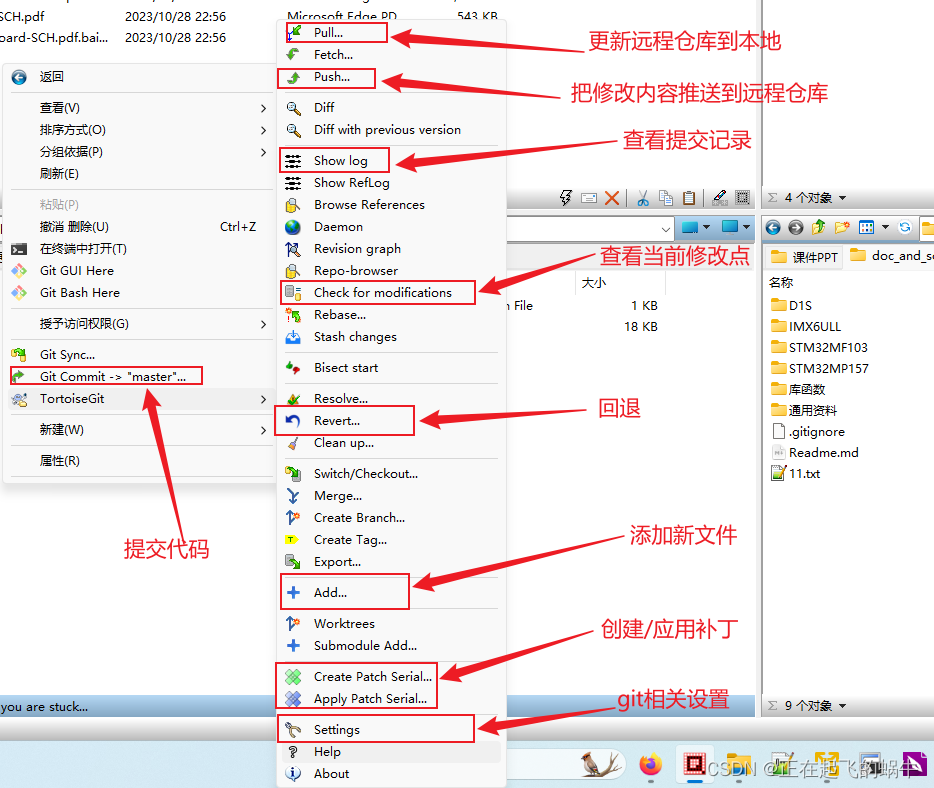
gitee提交代码步骤介绍(含git环境搭建)
1、gitee官网地址 https://gitee.com; 2、Windows中安装git环境 参考博客:《Windows中安装Git软件和TortoiseGit软件》; 3、设置用户名和密码 这里的用户名和密码就是登录gitee网站的用户名和密码如果设置错误,可以在Windows系统的“凭据管理…...

【MyBatis-Plus】常用的插件介绍(乐观锁、逻辑删除、分页)
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于MyBatis-Plus的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.为什么要使用MyBatis-Plus中的插…...
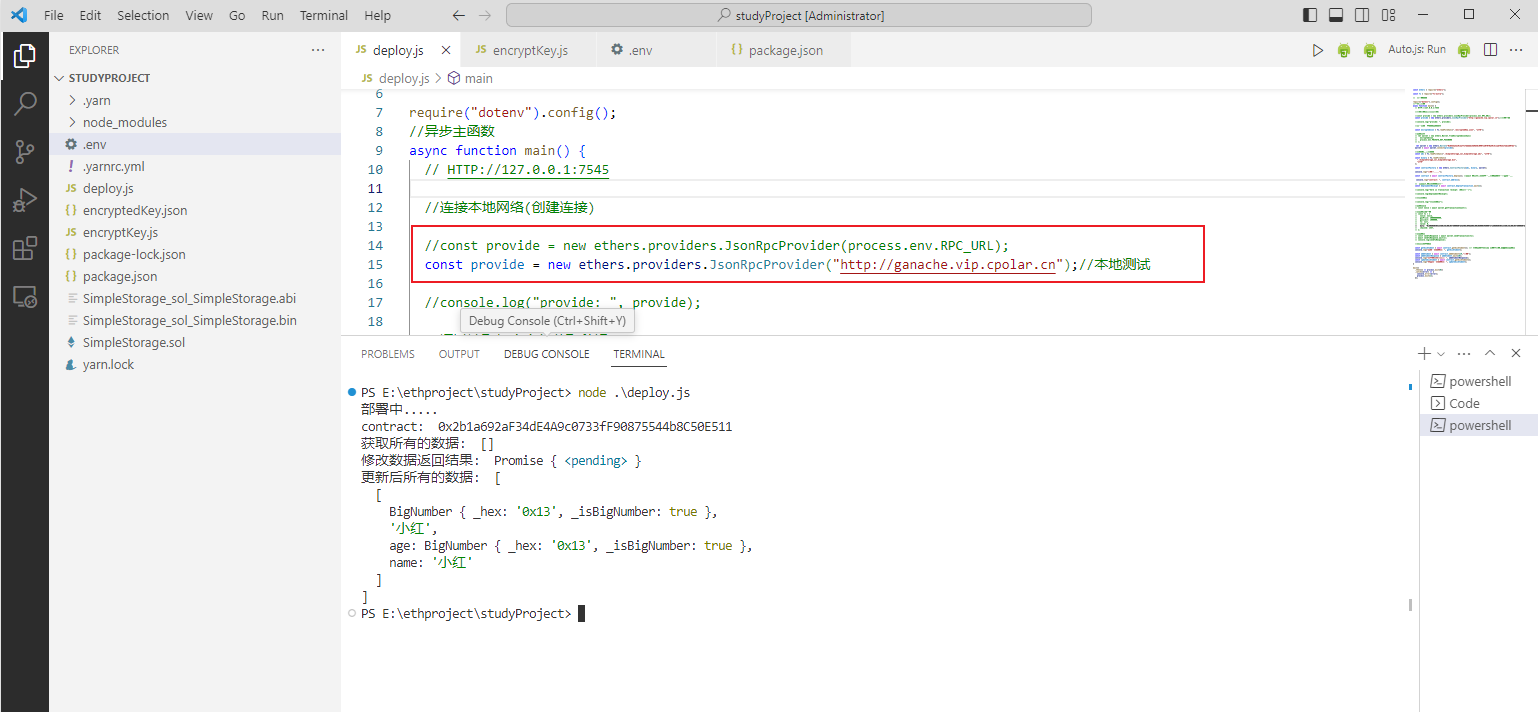
DApp测试网络Ganache本地部署并实现远程连接
文章目录 前言1. 安装Ganache2. 安装cpolar3. 创建公网地址4. 公网访问连接5. 固定公网地址 前言 Ganache 是DApp的测试网络,提供图形化界面,log日志等;智能合约部署时需要连接测试网络。 Ganache 是一个运行在本地测试的网络,通过结合cpol…...
好用的硬盘分区工具,傲梅分区助手 V10.2
傲梅分区助手软件可以帮助用户在硬盘上创建、调整、合并、删除分区,以及管理磁盘空间等操作。它可以帮助你进行硬盘无损分区操作。 支持系统 目前这款软件支持 Windows 7、Windows 8、Windows 10、Windows 11 等个人系统,还支持 Windows 2012/2016/2019…...

【华为鸿蒙系统学习】- HarmonyOS4.0开发|自学篇
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:"没有罗马,那就自己创造罗马~" 目录 HarmonyOS 4.0 技术介绍: HarmonyOS三大特征: 1.实现硬件互助&#…...
Qt图像处理-Qt中配置OpenCV打开本地图片
本文讲解Qt中配置OpenCV过程并用实例展示如何使用OpenCV打开图片(windows环境下) 一、下载OpenCv 本文使用版本OpenCV-MinGW-Build-OpenCV-3.4.5 下载地址: https://codeload.github.com/huihut/OpenCV-MinGW-Build/zip/refs/heads/OpenCV-3.4.5 点击Code-local-Downlo…...

HTML中RGB颜色表示法和RGBA颜色表示法
Hi i,m JinXiang ⭐ 前言 ⭐ 本篇文章主要介绍HTML中RGB颜色表示法和RGBA颜色表示法以及部分理论知识 🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁 🍉博主收将持续更新学习记录获,友友们有任何问题可以…...
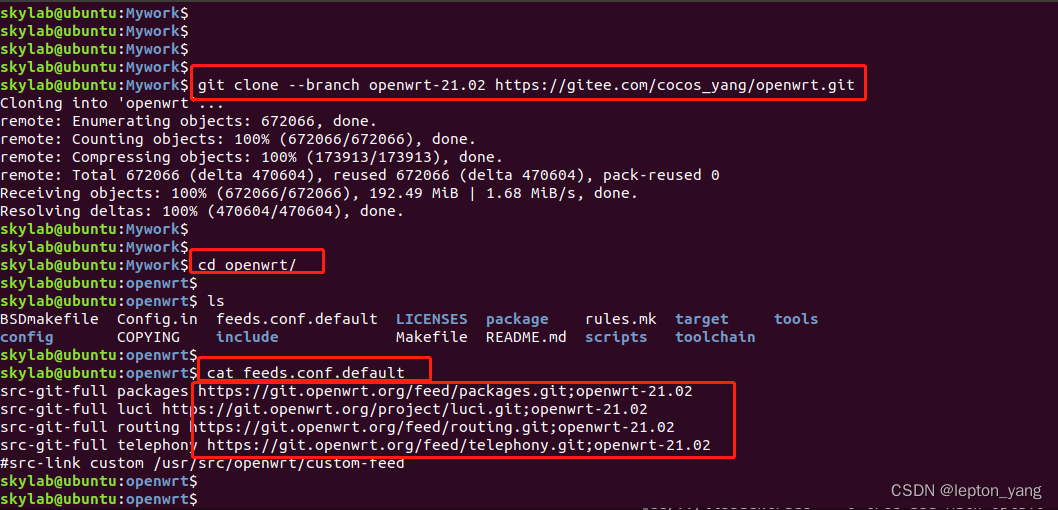
Openwrt源码下载出现“The remote end hung up unexpected”
最近项目原因需要下载openwrt21.02版本源码,花费了很多时间,找到正确方法后,发现可以节省很多时间,记录下过程,方便自己,可能方便他人。 一.问题阐述 openwrt21.02下载链接如下: git clone -…...
Cron表达式方案实例详解)
Spring定时任务动态更改(增、删、改)Cron表达式方案实例详解
Spring定时任务动态更改(增、删、改)Cron表达式方案实例详解 最近在做一个需求,用户可以在平台上配置任务计划数据(就是任务的执行和描述的相关信息,包括任务参数、cron表达式),配置后…...

常用登录加密之Shiro与Spring Security的使用对比
Shiro与Spring Security都是主流的身份认证和权限控制安全框架,Shiro偏向于前后端不分离平台,而Spring Security更偏向于前后端分离平台。接下来简单列一下两种登录验证的执行流程和示例,了解实际运用中的登录执行流程,然后重点剖…...
)
获取文件路径里的文件名(不包含扩展名)
“./abc/abc/llf.jpg” 写一个代码,让我获得“llf”这段字符串 import osfile_path "./abc/abc/llf.jpg" file_name os.path.splitext(os.path.basename(file_path))[0] print(file_name)在这个代码中,我们使用了os.path模块来处理文件路径…...
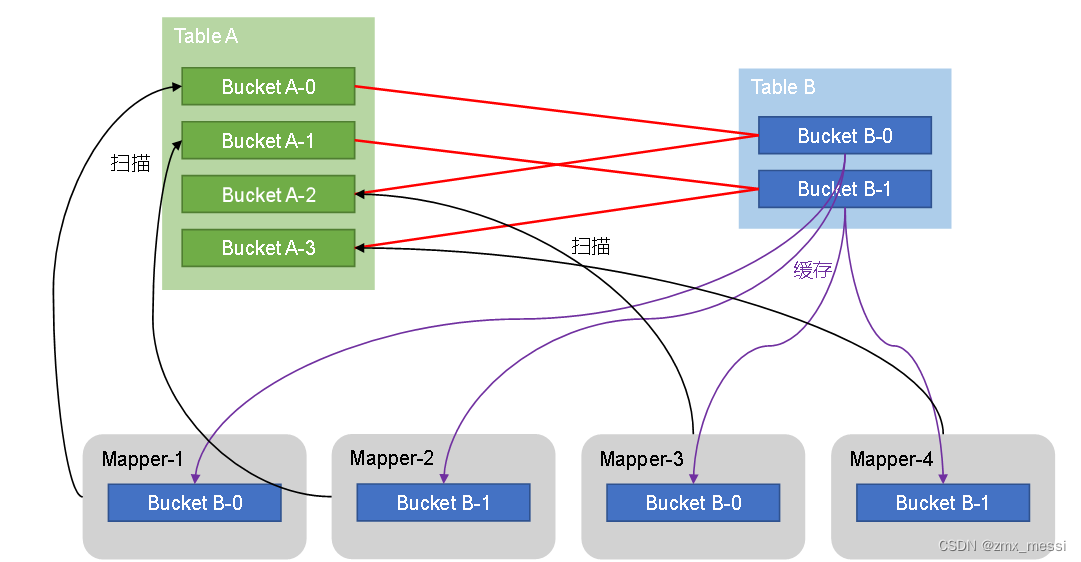
HiveSql语法优化二 :join算法
Hive拥有多种join算法,包括Common Join,Map Join,Bucket Map Join,Sort Merge Buckt Map Join等,下面对每种join算法做简要说明: Common Join Common Join是Hive中最稳定的join算法,其通过一个M…...

Leetcode—459.重复的子字符串【简单】
2023每日刷题(五十九) Leetcode—459.重复的子字符串 算法思想 巧解的算法思想 实现代码 从第一个位置开始到s.size()之前,看s字符串是否是ss的子串 class Solution { public:bool repeatedSubstringPattern(string s) {return (s s).fin…...
Mac安装Typora实现markdown自由
一、什么是markdown Markdown 是一种轻量级标记语言,创始人为约翰格鲁伯(John Gruber)。 它允许人们使用易读易写的纯文本格式编写文档,然后转换成有效的 XHTML(或者HTML)文档。这种语言吸收了很多在电子邮…...

前后端传参格式
前端发送 Serialize()方法 是指将一个抽象的JavaScript对象(数据结构)转换成字符串。这个字符串可以利用标准格式发送到服务器,被视为URL查询字符串或者POST数据,或者由于复杂的AJAX请求。这个方法使用的数据结构可以是JavaScri…...
【后端学前端】第三天 css动画 动态搜索框(定位、动态设置宽度)
1、学习信息 视频地址:css动画 动态搜索框(定位、动态设置宽度)_哔哩哔哩_bilibili 2、源码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>test3</title>…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
