动态规划——OJ题(一)

文章目录
- 一、第N个泰波那契数
- 1、题目讲解
- 2、思路讲解
- 3、代码实现
- 二、三步问题
- 1、题目讲解
- 2、思路讲解
- 3、代码实现
- 三、使用最小花费爬楼梯
- 1、题目讲解
- 2、思路讲解
- 3、代码实现
- 四、解码方法
- 1、题目讲解
- 2、思路讲解
- 3、代码实现
一、第N个泰波那契数
1、题目讲解

2、思路讲解
- 状态表⽰:
这道题可以「根据题⽬的要求」直接定义出状态表⽰:
dp[i] 表⽰:第 i 个泰波那契数的值。 - 状态转移⽅程:
题⽬已经⾮常贴⼼的告诉我们了:
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] - 初始化:
从我们的递推公式可以看出, dp[i] 在 i = 0 以及 i = 1 的时候是没有办法进⾏推导的,因
为 dp[-2] 或 dp[-1] 不是⼀个有效的数据。
因此我们需要在填表之前,将 0, 1, 2 位置的值初始化。题⽬中已经告诉我们 dp[0] = 0,
dp[1] = dp[2] = 1 。 - 填表顺序:
毫⽆疑问是「从左往右」。 - 返回值:
应该返回 dp[n] 的值。
3、代码实现
普通版
class Solution {
public:int tribonacci(int n) {if(n==0) return 0;if(n==1 || n==2) return 1;vector<int> dp(n+1);dp[0]=0,dp[1]=1,dp[2]=1;for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}return dp[n];}
};
空间优化版
class Solution {
public:int tribonacci(int n) {if(n==0) return 0;if(n==1 || n==2) return 1;int a=0,b=1,c=1,d=0;for(int i=3;i<=n;i++){d=a+b+c;a=b;b=c;c=d;}return d;}
};
二、三步问题
1、题目讲解

2、思路讲解
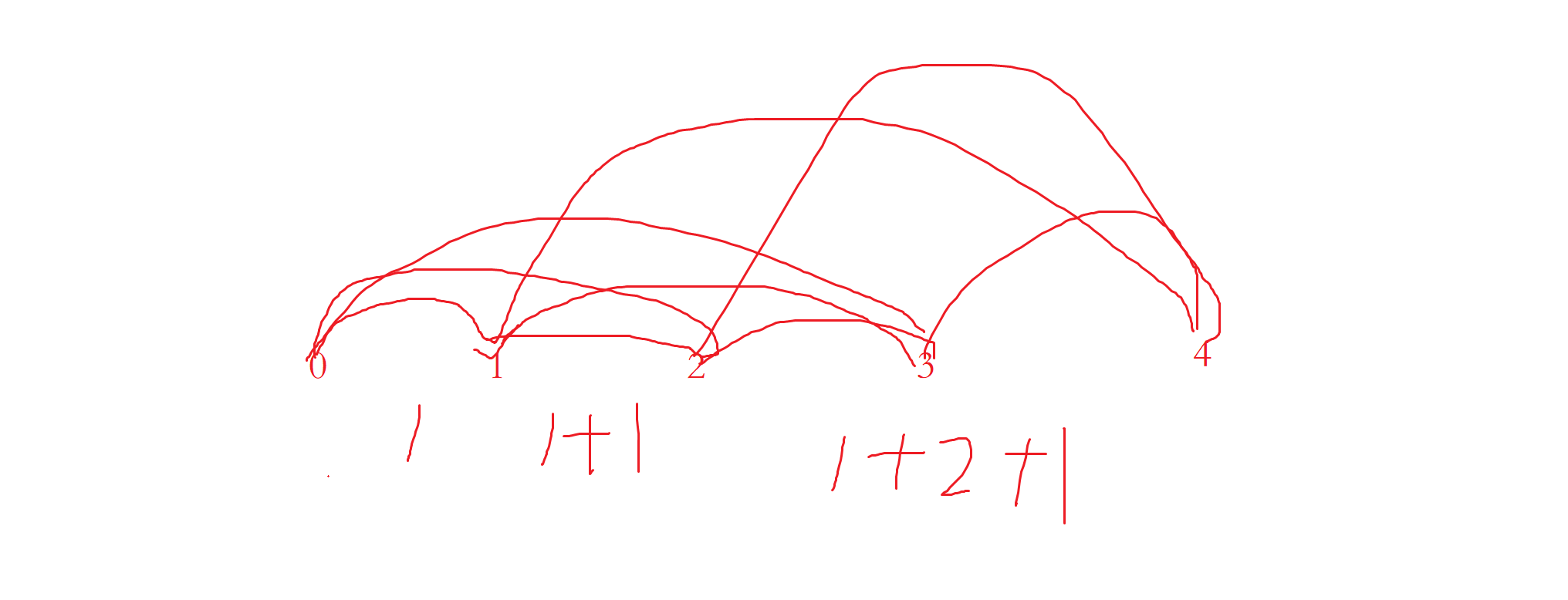
- 状态表⽰
这道题可以根据「经验 + 题⽬要求」直接定义出状态表⽰:
dp[i] 表⽰:到达 i 位置时,⼀共有多少种⽅法。 - 状态转移⽅程
以 i 位置状态的最近的⼀步,来分情况讨论:
如果 dp[i] 表⽰⼩孩上第 i 阶楼梯的所有⽅式,那么它应该等于所有上⼀步的⽅式之和:
i. 上⼀步上⼀级台阶, dp[i] += dp[i - 1] ;
ii. 上⼀步上两级台阶, dp[i] += dp[i - 2] ;
iii. 上⼀步上三级台阶, dp[i] += dp[i - 3] ;
综上所述, dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] 。
需要注意的是,这道题⽬说,由于结果可能很⼤,需要对结果取模。
在计算的时候,三个值全部加起来再取模,即 (dp[i - 1] + dp[i - 2] + dp[i - 3])
% MOD 是不可取的,同学们可以试验⼀下, n 取题⽬范围内最⼤值时,⽹站会报错 signed
integer overflow 。
对于这类需要取模的问题,我们每计算⼀次(两个数相加/乘等),都需要取⼀次模。否则,万⼀
发⽣了溢出,我们的答案就错了。 - 初始化
从我们的递推公式可以看出, dp[i] 在 i = 0, i = 1 以及 i = 2 的时候是没有办法进⾏
推导的,因为 dp[-3] dp[-2] 或 dp[-1] 不是⼀个有效的数据。
因此我们需要在填表之前,将 1, 2, 3 位置的值初始化。
根据题意, dp[1] = 1, dp[2] = 2, dp[3] = 4 。 - 填表顺序
毫⽆疑问是「从左往右」。 - 返回值
应该返回 dp[n] 的值。
3、代码实现
class Solution {
public:int waysToStep(int n) {if(n==1 || n==2) return n;if(n==3) return 4;const int MOD=1e9+7;vector<int> dp(n+1);dp[1]=1,dp[2]=2,dp[3]=4;for(int i=4;i<=n;i++){dp[i]= ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;}return dp[n];}
};
三、使用最小花费爬楼梯
1、题目讲解

2、思路讲解
方法一:
- 状态表⽰:
这道题可以根据「经验 + 题⽬要求」直接定义出状态表⽰:
第⼀种:以 i 位置为结尾,巴拉巴拉
dp[i] 表⽰:到达 i 位置时的最⼩花费。(注意:到达 i 位置的时候, i 位置的钱不需要
算上) - 状态转移⽅程:
根据最近的⼀步,分情况讨论:
▪ 先到达 i - 1 的位置,然后⽀付 cost[i - 1] ,接下来⾛⼀步⾛到 i 位置:
dp[i - 1] + csot[i - 1] ;
▪ 先到达 i - 2 的位置,然后⽀付 cost[i - 2] ,接下来⾛⼀步⾛到 i 位置:
dp[i - 2] + csot[i - 2] 。 - 初始化:
从我们的递推公式可以看出,我们需要先初始化 i = 0 ,以及 i = 1 位置的值。容易得到
dp[0] = dp[1] = 0 ,因为不需要任何花费,就可以直接站在第 0 层和第 1 层上。 - 填表顺序:
根据「状态转移⽅程」可得,遍历的顺序是「从左往右」。 - 返回值:
根据「状态表⽰以及题⽬要求」,需要返回 dp[n] 位置的值。
方法二:
- 状态表⽰:
这道题可以根据「经验 + 题⽬要求」直接定义出状态表⽰:
第⼆种:以 i 位置为起点,巴拉巴拉。
dp[i] 表⽰:从 i 位置出发,到达楼顶,此时的最⼩花费。 - 状态转移⽅程:
根据最近的⼀步,分情况讨论:
▪ ⽀付 cost[i] ,往后⾛⼀步,接下来从 i + 1 的位置出发到终点: dp[i + 1] +
cost[i] ;
▪ ⽀付 cost[i] ,往后⾛两步,接下来从 i + 2 的位置出发到终点: dp[i + 2] +
cost[i] ;
我们要的是最⼩花费,因此 dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i] 。 - 初始化:
为了保证填表的时候不越界,我们需要初始化最后两个位置的值,结合状态表⽰易得: dp[n -
1] = cost[n - 1], dp[n - 2] = cost[n - 2] - 填表顺序:
根据「状态转移⽅程」可得,遍历的顺序是「从右往左」。 - 返回值:
根据「状态表⽰以及题⽬要求」,需要返回 dp[n] 位置的值。
3、代码实现
方法一:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n+1);dp[0]=0,dp[1]=0;for(int i=2;i<=n;i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[n]; }
};
方法二:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n);dp[n-1]=cost[n-1],dp[n-2]=cost[n-2];for(int i=n-3;i>=0;i--){dp[i]=cost[i]+min(dp[i+1],dp[i+2]);}return min(dp[0],dp[1]);}
};
四、解码方法
1、题目讲解

2、思路讲解
-
状态表⽰:
根据以往的经验,对于⼤多数线性 dp ,我们经验上都是「以某个位置结束或者开始」做⽂章,这
⾥我们继续尝试「⽤ i 位置为结尾」结合「题⽬要求」来定义状态表⽰。
dp[i] 表⽰:字符串中 [0,i] 区间上,⼀共有多少种编码⽅法。 -
状态转移⽅程:
定义好状态表⽰,我们就可以分析 i 位置的 dp 值,如何由「前⾯」或者「后⾯」的信息推导出
来。
关于 i 位置的编码状况,我们可以分为下⾯两种情况:
i. 让 i 位置上的数单独解码成⼀个字⺟;
ii. 让 i 位置上的数与 i - 1 位置上的数结合,解码成⼀个字⺟。下⾯我们就上⾯的两种解码情况,继续分析:
让 i 位置上的数单独解码成⼀个字⺟,就存在「解码成功」和「解码失败」两种情况:
i. 解码成功:当 i 位置上的数在 [1, 9] 之间的时候,说明 i 位置上的数是可以单独解
码的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 1] 区间上的解码⽅法。因为 [0, i - 1] 区间上的所有解码结果,后⾯填上⼀个 i 位置解码后的字⺟就可以了。此时 dp[i] = dp[i - 1] ;ii. 解码失败:当 i 位置上的数是 0 的时候,说明 i 位置上的数是不能单独解码的,那么
此时 [0, i] 区间上不存在解码⽅法。因为 i 位置如果单独参与解码,但是解码失败
了,那么前⾯做的努⼒就全部⽩费了。此时 dp[i] = 0 。
让 i 位置上的数与 i - 1 位置上的数结合在⼀起,解码成⼀个字⺟,也存在「解码成功」和「解码失败」两种情况:
i. 解码成功:当结合的数在 [10, 26] 之间的时候,说明 [i - 1, i] 两个位置是可以
解码成功的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 2 ] 区间上的解码
⽅法,原因同上。此时 dp[i] = dp[i - 2] ;
ii. 解码失败:当结合的数在 [0, 9] 和 [27 , 99] 之间的时候,说明两个位置结合后解码失败(这⾥⼀定要注意 00 01 02 03 04 … 这⼏种情况),那么此时 [0, i] 区间上的解码⽅法就不存在了,原因依旧同上。此时 dp[i] = 0 。综上所述: dp[i] 最终的结果应该是上⾯四种情况下,解码成功的两种的累加和(因为我们关⼼
的是解码⽅法,既然解码失败,就不⽤加⼊到最终结果中去),因此可以得到状态转移⽅程
( dp[i] 默认初始化为 0 ):
i. 当 s[i] 上的数在 [1, 9] 区间上时: dp[i] += dp[i - 1] ;
ii. 当 s[i - 1] 与 s[i] 上的数结合后,在 [10, 26] 之间的时候: dp[i] +=
dp[i - 2] ;
如果上述两个判断都不成⽴,说明没有解码⽅法, dp[i] 就是默认值 0 。
3、代码实现
优化前:
class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int> dp(n);dp[0]=s[0]!='0';if(n==1) return dp[0];if(s[1]!='0' && s[0]!='0') dp[1]++;int t=(s[0]-'0')*10+(s[1]-'0');if(t>=10 && t<=26) dp[1]++;for(int i=2;i<n;i++){if(s[i]!='0') dp[i]+=dp[i-1];int t=(s[i-1]-'0')*10+(s[i]-'0');if(t>=10 && t<=26) dp[i]+=dp[i-2];}return dp[n-1];}
};优化后:
class Solution {
public:int n=s.size();vector<int> dp(n+1);dp[0]=1;dp[1]=s[1-1]!='0';for(int i=2;i<=n;i++){if(s[i-1]!='0') dp[i]+=dp[i-1];int t=(s[i-2]-'0')*10+(s[i-1]-'0');if(t>=10 && t<=26) dp[i]+=dp[i-2];}return dp[n];}
};
相关文章:

动态规划——OJ题(一)
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、第N个泰波那契数1、题目讲解2、思路讲解3、代码实现 二、三步问题1、题目讲解2、思路讲解…...
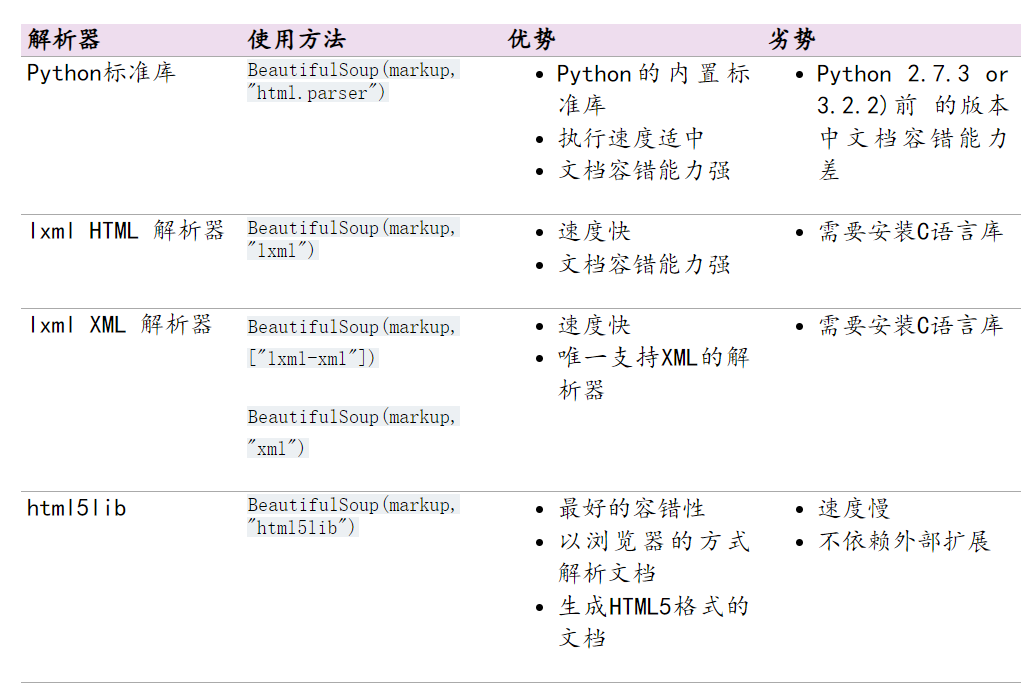
六:爬虫-数据解析之BeautifulSoup4
六:bs4简介 基本概念: 简单来说,Beautiful Soup是python的一个库,最主要的功能是从网页抓取数据官方解释如下: Beautiful Soup提供一些简单的、python式的函数用来处理导航、搜索、修改分析树等功能。 它是一个工具箱…...

音频筑基:总谐波失真THD+N指标
音频筑基:总谐波失真THDN指标 THDN含义深入理解 在分析音频信号中,THDN指标是我们经常遇到的概念,这里谈谈自己的理解。 THDN含义 首先,理解THD的定义: THD,Total Harmonic Distortion,总谐波…...
自动驾驶技术:驶向未来的智能之路
导言 自动驾驶技术正引领着汽车产业向着更安全、高效、智能的未来演进。本文将深入研究自动驾驶技术的核心原理、关键技术、应用场景以及对交通、社会的深远影响。 1. 简介 自动驾驶技术是基于先进传感器、计算机视觉、机器学习等技术的创新,旨在实现汽车在不需要人…...

TIGRE: a MATLAB-GPU toolbox for CBCT image reconstruction
TIGRE: 用于CBCT图像重建的MATLAB-GPU工具箱 论文链接:https://iopscience.iop.org/article/10.1088/2057-1976/2/5/055010 项目链接:https://github.com/CERN/TIGRE Abstract 本文介绍了基于层析迭代GPU的重建(TIGRE)工具箱,这是一个用于…...

我的NPI项目之Android 安全系列 -- EMVCo
最近一直在和支付有关的内容纠缠,原来我负责的产品后面还要过EMVCo的认证。于是,就网上到处找找啥事EMVCo,啥是EMVCo,啥是EMVCo。 于是找到了一个神奇的个人网站:Ganeshji Marwaha 虽然时间有点久远,但是用…...
vue中实现使用相框点击拍照,canvas进行前端图片合并下载
拍照和相框合成,下载图片dome 一、canvas介绍 Canvas是一个HTML5元素,它提供了一个用于在网页上绘制图形、图像和动画的2D渲染上下文。Canvas可以用于创建各种图形,如线条、矩形、圆形、文本等,并且可以通过JavaScript进行编程操作。 Canvas元素本身是一个矩形框,可以通…...

边缘检测@获取labelme标注的json黑白图掩码mask
import cv2 as cv import numpy as np import json import os from PIL import Imagedef convertPolygonToMask(jsonfilePath):...

嵌入式培训-数据结构-day23-线性表
线性表 线性表是包含若干数据元素的一个线性序列 记为: L(a0, ...... ai-1, ai, ai1 ...... an-1) L为表名,ai (0≤i≤n-1)为数据元素; n为表长,n>0 时,线性表L为非空表,否则为空表。 线性表L可用二元组形式描述…...
C# DotNetCore AOP简单实现
背景 实际开发中业务和日志尽量不要相互干扰嵌套,否则很难维护和调试。 示例 using System.Reflection;namespace CSharpLearn {internal class Program{static void Main(){int age 25;string name "bingling";Person person new(age, name);Conso…...

19.Tomcat搭建
Tomcat 简介 Tomcat的安装和启动 前置条件 • JDK 已安装(JAVA_HOME环境变量已被成功配置) Windows 下安装 访问 http://tomcat.apache.org ⇒ 左侧边栏 “Download” 2. 解压缩下载的文件到 “D:\tomcat”, tomcat的内容最终被解压到 “D:\tomcat\apache-tomcat-9.0.84” 3.…...

HarmonyOS云开发基础认证考试满分答案(100分)【全网最全-不断更新】【鸿蒙专栏-29】
系列文章: HarmonyOS应用开发者基础认证满分答案(100分) HarmonyOS应用开发者基础认证【闯关习题 满分答案】 HarmonyOS应用开发者高级认证满分答案(100分) HarmonyOS云开发基础认证满分答案(100分…...

Unity项目里Log系统该怎么设计
其实并没有想完整就设计一个好用的Log系统,然后发出来。记录这个的原因,是在书里看到这么一句话,Log会消耗资源,特别是写文件,因此可以设置一个Log缓冲区,等缓冲区满了再一次性写入文件,以节省资…...

设计模式-状态(State)模式
目录 开发过程中的一些场景 状态模式的简单介绍 状态模式UML类图 类图讲解 适用场景 Java中的例子 案例讲解 什么是状态机 如何实现状态机 SpringBoot状态自动机 优点 缺点 与其他模式的区别 小结 开发过程中的一些场景 我们在平时的开发过程中,经常会…...

oracle怎么存放json好
Oracle数据库提供了多种方式来存储JSON数据。你可以将JSON数据存储在VARCHAR2、CLOB或BLOB数据类型中,或者使用Oracle提供的JSON数据类型。 如果你选择使用VARCHAR2数据类型来存储JSON数据,你可以直接将JSON字符串存储在其中。例如: CREATE…...

【计算机网络】—— 详解码元,传输速率的计算|网络奇缘系列|计算机网络
🌈个人主页: Aileen_0v0🔥系列专栏: 一见倾心,再见倾城 --- 计算机网络~💫个人格言:"没有罗马,那就自己创造罗马~" 目录 码元 速率和波特 思考1 思考2 思考3 带宽(Bandwidth) 📝总结 码元…...
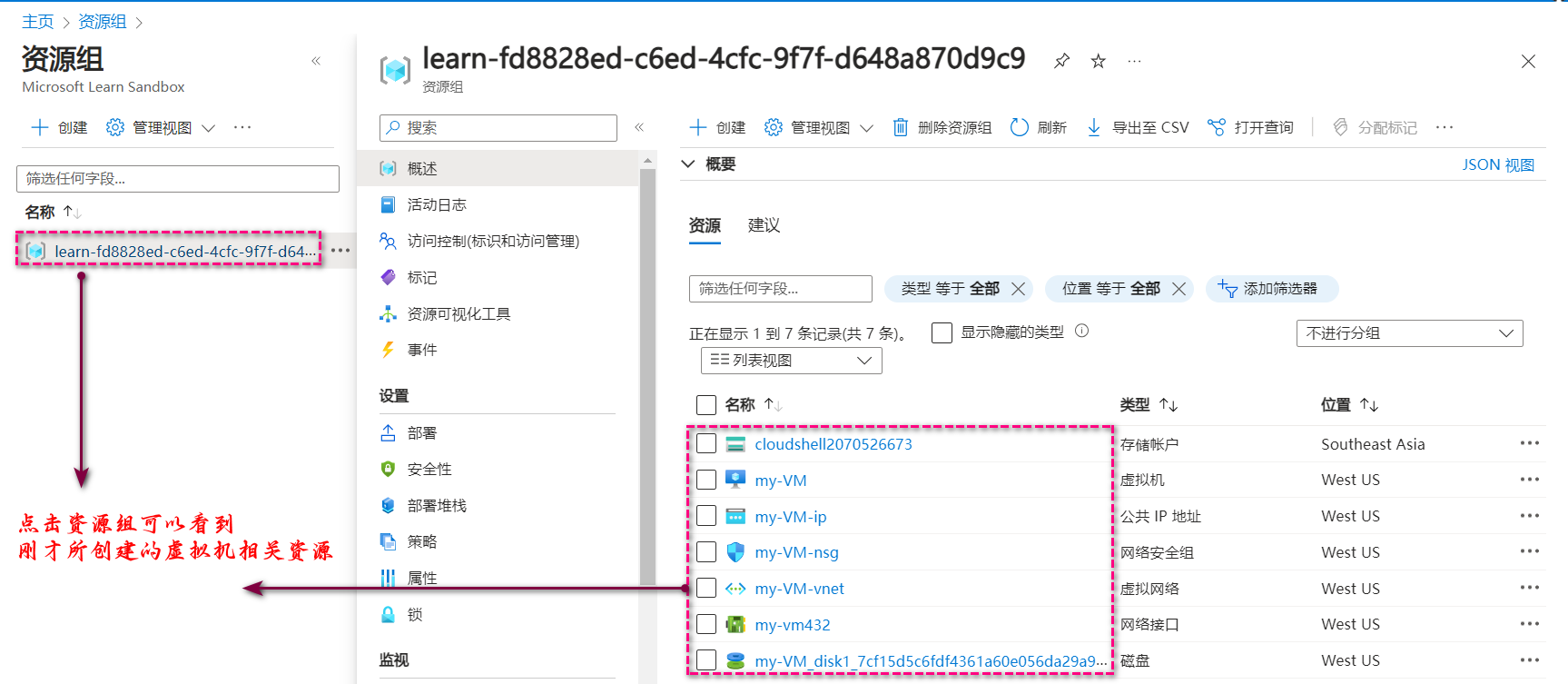
[ 云计算 | Azure 实践 ] 在 Azure 门户中创建 VM 虚拟机并进行验证
文章目录 一、前言二、在 Azure Portal 中创建 VM三、验证已创建的虚拟机资源3.1 方法一:在虚拟机服务中查看验证3.1 方法二:在资源组服务中查看验证 四、文末总结 一、前言 本文会开始创建新系列的专栏,专门更新 Azure 云实践相关的文章。 …...
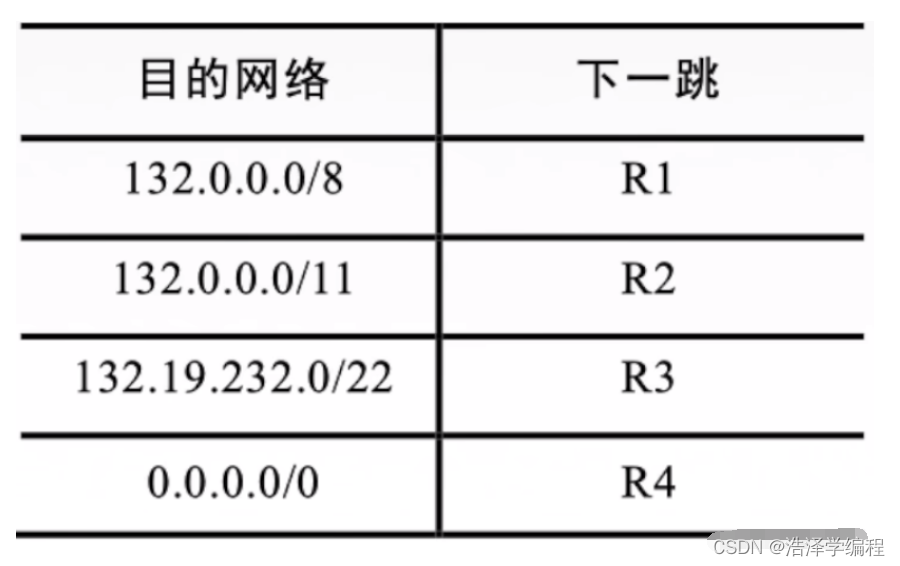
计算机网络:网络层(无分类编址CIDR、计算题讲解)
带你快速通关期末 文章目录 前言一、无分类编址CIDR简介二、构成超网三、最长前缀匹配总结 前言 我们在前面知道了分类地址,但是分类地址又有很多缺陷: B类地址很快将分配完毕!路由表中的项目急剧增长! 一、无分类编址CIDR简介 无分类域间路由选择CI…...

Learning Semantic-Aware Knowledge Guidance forLow-Light Image Enhancement
微光图像增强(LLIE)研究如何提高照明并生成正常光图像。现有的大多数方法都是通过全局和统一的方式来改善低光图像,而不考虑不同区域的语义信息。如果没有语义先验,网络可能很容易偏离区域的原始颜色。为了解决这个问题࿰…...

关于嵌入式开发的一些信息汇总:开发模型以及自托管开发(二)
关于嵌入式开发的一些信息汇总:开发模型及自托管开发(二) 2 自托管开发2.2 构建 Raspberry Pi 内核2.3 安装内核2.4 总结 3 连接目标板3.1 Raspberry Pi 上的网络设置3.2 Ssh、rsh、rlogin 和 telnet 连接到目标 4 应用程序开发4.1 在目标板上…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
