C++ STL泛型算法
泛型算法
<algorithm>定义了大约 80 个标准算法。
它们操作由一对迭代器定义的(输入)序列或单一迭代器定义的(输出)序列。
当对两个序列进行拷贝、比较操作时,第一个序列由一对迭代器[b,e)表示,但第二个序列只由一个迭代器b2表示,b2指出了序列的起始位置。
应当保证第二个序列包含足够多的的元素供算法使用。
大多数标准库算法返回迭代器;特别是,它们不返回结果的容器。
大多数标准库算法都有两个版本:
- 一个“普通”版本使用常规操作(如
<和==)完成其任务。 - 另一个版本接受关键操作参数
在某些情况下,实参既可以解释为谓词,也可以解释为值。
不修改序列的算法
for_each()
最简单的算法是 for_each(),它简单地对序列中的每个元素执行指定操作。
vector<int> v{ 2,4,6,8 };for_each( v.begin(), v.end(), [](int x) {cout << x << ' '; } );/* 输出 2 4 6 8 */
| 算法 | 功能 |
|---|---|
| f = for_each(b,e,f); | 对[b,e)中的每个 x 执行f(x),返回 f |
序列谓词
vector<int> v{ 2,4,6,8 };auto flag = all_of(v.begin(), v.end(), [](int x) { return x > 0; });cout << flag << endl; // v 中的每个元素大于 0 ,输出 1
当一个序列谓词失败时,它不会告知我们是哪个元素导致了失败。
vector<int> v{ 0,4,8,3 };auto flag = any_of(v.begin(), v.end(), [](int x) { return x > 5; });cout << flag << endl; //有元素大于 5 ,但不知道是哪个元素大于5
| 算法 | 功能 |
|---|---|
| all_of(b,e,f); | [b,e)中所有 x 都满足f(x)吗? |
| any_of(b,e,f); | [b,e)中某个 x 满足f(x)吗? |
| none_of(b,e,f); | [b,e)中所有 x 都不满足f(x)吗? |
count()
vector<int> v{ 1,0,1,1,3 };cout << count(v.begin(), v.end(), 1) << endl; // 1 的数目为 3,输出 3
| 算法 | 功能 |
|---|---|
| x = count(b,e,v); | x 为[b,e)中满足v==*p的元素,*p的数目 |
| x = count_if(b,e,f); | x 为[b,e)中满足f(*p)的元素,*p的数目 |
find()
find() 系列算法顺序搜索具有特定值或令谓词为真的元素。
谓词是一个可调用的表达式,其结果是一个能用作条件的值。
算法 find() 和 find_if() 都返回一个迭代器,分别指向匹配给定值和给定谓词的第一个元素。
vector<char> v{ 'e','E','d','E','A'};auto p = find(v.begin(),v.end(),'E');cout << *p << endl; //输出 Ecout << *(p + 1) << endl; //输出 d
算法 find_first_of() 查找序列中与另一个序列中元素相等的第一个元素。
vector<char> v{ 'e','E','d','B','b' };array<char, 4> arr{ 'A','B','C','D' };auto p = find_first_of( v.begin(),v.end(),arr.begin(),arr.end() );cout << *p << endl; //输出 B
| 算法 | 功能 |
|---|---|
| p = find(b,e,v); | p 指向[b,e)中第一个满足v==*p的元素 |
| p = find_if(b,e,f); | p 指向[b,e)中第一个满足f(*p)的元素 |
| p = find_if_not(b,e,f); | p 指向[b,e)中第一个满足!f(*p)的元素 |
| p = find_first_of(b1,e1,b2,e2); | p 指向[b1,e1)中第一个满足*p==*q的元素,其中 q 指向[b2,e2)中的某个元素 |
| p = find_first_of(b1,e1,b2,e2,f); | p 指向[b1,e1)中第一个满足f(*p,*q)的元素,其中 q 指向[b2,e2)中的某个元素 |
| p = adjacent_find(b,e); | p 指向[b,e)中第一个满足*p==*(p+1)的元素 |
| p = adjacent_find(b,e,f); | p 指向[b,e)中第一个满足f(*p,*(p+1))的元素 |
| p = find_end(b1,e1,b2,e2); | p 指向[b1,e1)中最后一个满足*p==*q的元素,其中 q 指向[b2,e2)中的某个元素 |
| p = find_end(b1,e1,b2,e2,f); | p 指向[b1,e1)中最后一个满足f(*p,*q)的元素,其中 q 指向[b2,e2)中的某个元素 |
equal()
算法 equal() 比较两个序列中的元素是否都相同。
vector<char> v{ 'A','B','C','D','b' };array<char, 4> arr{ 'A','B','C','D' };auto b = equal( v.begin(),v.end() -1 ,arr.begin(),arr.end() );cout << b << endl; //输出 1
| 算法 | 功能 |
|---|---|
| equal(b,e,b2); | [b,e)和[b2,b2+(e-b))中所有对应元素都满足v == v2? |
| equal(b,e,b2,f); | [b,e)和[b2,b2+(e-b))中所有对应元素都满足f(v,v2)? |
mismatch()
算法 mismatch() 查找两个序列中第一对不匹配的元素,返回指向这两个元素的迭代器。
并没有参数指出第二个序列的末尾;算法假定第二个序列中至少包含与第一个序列一样多的元素。
vector<char> v{ 'A','B','e','D' };array<char, 4> arr{ 'A','B','C','D' };auto p = mismatch( v.begin(),v.end() ,arr.begin() );cout << *(p.first) << endl; //输出 ecout << *(p.second) << endl; //输出 C
| 算法 | 功能 |
|---|---|
| pair(p1,p2) = mismatch(b,e,b2); | p1 指向[b,e)中第一个满足!(*p1 == *p2)的元素,p2 指向[b2,b2+(e-b))中对应的元素;若不存在这样的元素,则p1 == e |
| pair(p1,p2) = mismatch(b,e,b2,f); | p1 指向[b,e)中第一个满足!f(*p1,*p2)的元素,p2 指向[b2,b2+(e-b))中对应的元素;若不存在这样的元素,则p1 == e |
search()
算法 search() 和 search_n() 查找给定序列是否是另一个序列的子序列。
vector<char> v{ 'E','A','B','C','D' };array<char, 3> arr{ 'A','B','C' } ;auto p = search(v.begin(), v.end(), arr.begin(), arr.end());cout << *p << endl; //输出 A;'A','B','C' 是 'E','A','B','C','D' 的子序列
| 算法 | 功能 |
|---|---|
| p = serach(b,e,b2,e2); | p 指向[b,e)中第一个满足[p,p+(e2-b2))中等于[b2,e2)的*p |
| p = serach(b,e,b2,e2,f); | p 指向[b,e)中第一个满足[p,p+(e2-b2))中等于[b2,e2)的*p,用 f 比较元素 |
| p = serach_n(b,e,n,v); | p 指向[b,e)中第一个满足[p,p+n)间所有元素的值均为 v 的位置 |
| p = serach_n(b,e,n,v,f); | p 指向[b,e)中第一个满足[p,p+n)间每个元素*q均满足f(*p,v)的位置 |
修改序列的算法
transform()
数据写入操作不能超出目标序列的末尾。
array<char, 4> arr{ 'A','B','C','D' };vector<char> v{ 'E','A','B','C','Z'};transform(arr.begin(), arr.end(), v.begin(), [](char x) { return x += 32; });/* V 中的元素变为:a b c d Z */
输出和输入可能是同一个序列。
vector<char> v{ 'E','A','B','C','Z'};transform(v.begin(), v.end(), v.begin(), [](char x) { return x += 32; });/* V 中的元素变为:e a b c z */
| 算法 | 功能 |
|---|---|
| p = transform(b,e,out,f); | 对[b,e)中的每个元素*p1应用*q = f(*p1),结果写入[out,out + (e - b)中的对应元素*q; p = out + (e - b) |
| p = transform(b,e,b2,out,f); | 对[b,e)中的每个元素*p1及其在[b2,b2 + (e - b))中的对应元素*p2*应用*q = f(*p1,*p2),结果写入[out,out + (e - b)中的对应元素*q; p = out + (e - b) |
copy()
copy() 系列算法从一个序列拷贝至另一个序列。
为了读取一个序列,需要一对迭代器描述起始位置和结尾位置;为了向序列中写入数据,则只需一个迭代器。
array<int,4> arr { 1,3,5,7 };vector<int> v{ 2,4,6,8 };auto p =copy( arr.begin(),arr.end(),v.begin() ); /* v 内的元素变为 1 3 5 7 */cout<< * (p-1) << endl; //输出 7;p = arr.end()
数据写入操作不能超出目标序列的末尾;但是,可以使用一个插入器按需增长目标序列。
array<int,4> arr { 1,3,5,7 };vector<int> v{ 2,4,6,8 };copy(arr.begin(), arr.end(), back_inserter(v));/* v 内的元素变为 2 4 6 8 1 3 5 7 */
拷贝算法的目标序列不一定是一个容器,任何可用一个输出迭代器描述的东西都可以作为它的目标。
| 算法 | 功能 |
|---|---|
| p = copy(b,e,out); | 将[b,e)中所有元素拷贝至 [out,p); p = out + (e - b) |
| p = copy_if(b,e,out,f); | 将[b,e)中满足f(x)的元素 x 拷贝至[out,p) |
| p = copy_n(b,n,out); | 将[b,b+n)间的前 n 个元素拷贝至 [out,p); p = out + n |
| p = copy_backward(b,e,out); | 将[b,e)中的所有元素拷贝至 [out,p),从尾元素开始拷贝; p = out + (e - b) |
| p = move(b,e,out); | 将[b,e)中所有元素移动至 [out,p); p = out + (e - b) |
| p = move_backward(b,e,out); | 将[b,e)中的所有元素移动至 [out,p),从尾元素开始移动; p = out + (e - b) |
unique()
算法 unique() 将不重复的元素移动到序列的头部,并返回指向不重复元素末尾位置的迭代器。
vector<char> v{ 'A','A','C','E','E','B'};auto p = unique(v.begin(), v.end()); auto iter = v.begin();while (iter != p){cout << *iter++ << ' ';}cout << endl;/* 输出: A C E B */
为了从一个容器中删除重复元素,必须显示地收缩容器。
vector<char> v{ 'A','A','C','E','E','B'};auto p = unique(v.begin(), v.end()); v.erase(p,v.end());
| 算法 | 功能 |
|---|---|
| p = unique(b,e); | 移动[b,e]中的一些元素,使得[b,p)中无连续重复元素 |
| p = unique(b,e,f); | 移动[b,e]中的一些元素,使得[b,p)中无连续重复元素;“重复”由f(*p,*(p+1))判定 |
| p = unique_copy(b,e,out); | 将[b,e)中的元素拷贝至 [out,p);不拷贝连续重复元素 |
| p = unique_copy(b,e,out,f); | 将[b,e)中的元素拷贝至 [out,p);不拷贝连续重复元素;“重复”由f(*p,*(p+1))判定 |
remove()
算法 remove() "删除"序列末尾的元素;它是通过将元素移动到左侧来实现“删除”的。
vector<char> v{ 'A','B','C','E','E','D' };auto p = remove(v.begin(), v.end(),'E');auto iter = v.begin();while (iter != p){cout << *iter++ << ' ';}cout << endl;/*输出:A B C D*/
| 算法 | 功能 |
|---|---|
| p = remove(b,e,v); | 从[b,e]中删除值为 v 元素,使得[b,p)中的元素都满足!(*q == v) |
| p =remove(b,e,f); | 从[b,e]中删除元素*q,使得[b,p)中的元素都满足!f(*q) |
| p = remove_copy(b,e,out,v); | 将[b,e)中满足!(*q == v)的元素拷贝至 [out,p) |
| p = remove_copy_f(b,e,out,f); | 将[b,e)中满足!f(*q)的元素拷贝至 [out,p) |
raplace()
算法 raplace() 将新值赋予选定的元素。
vector<char> v{ 'E','A','E','B','C','D' };replace(v.begin(), v.end(),'E','F'); // 将 E 替换为 F/* v 内的元素变为 F A F B C D */
| 算法 | 功能 |
|---|---|
| p = raplace(b,e,v,v2); | 将[b,e)中满足*p == v的元素替换为 v2 |
| p =raplace(b,e,f,v2); | 将[b,e)中满足f(*p)的元素替换为 v2 |
| p =raplace_copy(b,e,out,v,v2); | 将[b,e)中的元素拷贝至 [out,p),其中满足*p == v的元素被替换为 v2 |
| p = raplace_copy_f(b,e,out,f,v2); | 将[b,e)中的元素拷贝至 [out,p),其中满足f(*p,v)的元素被替换为 v2 |
rotable() 、 random_shuffle() 和 partition()
算法 rotable() 、 random_shuffle() 和 partition() 提供了移动序列中元素的系统方法。
rotable()(以及洗牌和划分算法)是用 swap() 来移动元素的。
rotable()
vector<char> v{ 'A','B','C','D','E' };auto p = rotate(v.begin(),v.begin()+2, v.end());/* v 内的元素变为 C D E A B */cout << *p << endl; // *p = A
| 算法 | 功能 |
|---|---|
| p = rotable(b,m,e); | 循环左移元素;将[b,e]看作一个环(首元素在尾元素之后);将*(b+i)移动到*( b + (i+(e-m))%(e-b) );*b移动到*m;p = b+(e-m) |
| p = rotable_copy(b,m,e,out); | 将[b,e]中的元素循环左移拷贝至[out,p) |
random_shuffle()
默认情况下,random_shuffle() 用均匀分布随机数发生器洗牌序列。
即,它选择序列元素的一个排列,使得每种排列被选中的概率相等。
vector<char> v{ 'A','D','C','B','E' };random_shuffle(v.begin(),v.end());/* v 内的元素变为 E D B C A */
| 算法 | 功能 |
|---|---|
| random_shuffle(b,e); | 洗牌[b,e]中的元素,使用默认随机数发生器 |
| random_shuffle(b,e,f); | 洗牌[b,e]中的元素,使用随机数发生器 f |
| shuffle(b,e,f); | 洗牌[b,e]中的元素,使用均匀分布随机数发生器 f |
partition()
划分算法基于某种划分标准将序列分为两部分。
vector<char> v{ 'A','H','C','B','F' };auto p = partition(v.begin(), v.end(), [](char x) {return x < 'E'; });/* v 内的元素变为 A C B H F */cout << *p << endl; // *p = H
| 算法 | 功能 |
|---|---|
| p = partition(b,e,f); | 将满足f(*p1)的元素置于区间[b,p)内,将其它元素置于区间[p,e)内 |
| p = stable_partition(b,e,f); | 将满足f(*p1)的元素置于区间[b,p)内,将其它元素置于区间[p,e)内;保持相对顺序 |
| pair(p1,p2) = partition_copy(b,e,out1,out2,f); | 将[b,e)中满足f(*p)的元素拷贝到[out1,p1)内,将[b,e)中满足!f(*p)的元素拷贝到[out2,p2)内 |
| p = partition_point(b,e,f); | 对[b,e),p 指向满足all_of(b,p,f)且none_of(b,p,f)的位置 |
| is_partitioned(b,e,f); | [b,e)中满足f(*p)的元素都在满足!f(*p)的元素之前吗? |
排列
例:打印序列 ABC 的所有排列组合:
vector<char> v{ 'A','B','C' };bool x = true;while ( x ){x = next_permutation(v.begin(), v.end());for (auto i : v)cout << i << ' ';cout << endl;}/* 输出:A C BB A CB C AC A BC B AA B C*/
算法 next_permutation() 接受一个序列,将其变换为下一个排列。
"下一个"的定义基于这样一个假设:所有的排列组合已按字典序排序。
如果存在”下一个“排列组合,next_permutation() 返回 true;否则,它将序列变换为升序中排在第一位的排列组合(例中的 ABC),并返回 false;
| 算法 | 功能 |
|---|---|
| x = next_permutation(b,e); | 将[b,e)变换为字典序上的下一个排列 |
| x = next_permutation(b,e,f); | 将[b,e)变换为字典序上的下一个排列;用 f 比较元素 |
| x = prev_permutation(b,e); | 将[b,e)变换为字典序上的前一个排列 |
| x = prev_permutation(b,e,f); | 将[b,e)变换为字典序上的前一个排列;用 f 比较元素 |
| is_permutation(b,e,b2); | [b2,b2+(e-b))是[b,e)的一个排列? |
| is_permutation(b,e,f); | [b2,b2+(e-b))是[b,e)的一个排列?用 f(*q,*p) 比较元素 |
fill()
fill() 系列算法提供了向序列元素赋值和初始化元素的方法。
算法 fill() 反复用指定值进行赋值。
vector<char> v{ 'A','H','C','B','F' };fill(v.begin(), v.end(), 'E');/* v 内的元素变为 E E E E E */
算法 generate() 则通过反复调用其函数实参得到的值进行赋值。
vector<char> v{ 'A','H','C','B','F' };int i = 0;generate( v.begin(), v.end(), [&i] { ++i; return 'A'+ i; } );/* v 内的元素变为 B C D E F */
算法 uninitialized_fill() 或 uninitialized_copy() 的目标元素必须是内置类型或是未初始化的。
| 算法 | 功能 |
|---|---|
| fill(b,e,v); | 将 v 赋予[b,e)中的每一个元素 |
| p = fill_n(b,n,v); | 将 v 赋予[b,b+n)中的每一个元素;p = b+n |
| generate(b,e,f); | 将 f() 赋予[b,e)中的每一个元素 |
| p = generate_n(b,n,f); | 将 f() 赋予[b,b+n)中的每一个元素;p = b+n |
| uninitialized_fill(b,e,v); | 将[b,e)中的每一个元素初始化为 v |
| p = uninitialized_fill_n(b,n,v); | 将[b,b+n)中的每一个元素初始化为 v;p = b+n |
| uninitialized_copy(b,e,out); | 将[out,out+(e-b))中的每一个元素初始化为[b,e)中对应的元素;p = out+(e-b) |
| p = uninitialized_copy_n(b,n,out); | 将[out,out+n]中的每一个元素初始化为[b,b+n)中对应的元素;p = out+n |
排序和搜索
排序
默认的比较操作是<运算符;值 a 和 b 的相等性通过!(a<b)&&!(b<a)来判定,而不是使用==运算符。
算法 sort() 要求使用随机访问迭代器。
基础的 sort() 算法很高效,平均时间复杂性为 O ( N ∗ log ( N ) ) O(N*\log(N)) O(N∗log(N))。。
如果需要一个稳定的排序算法,可以使用 stable_sort(),其平均时间复杂性为 O ( N ∗ log ( N ) log ( N ) ) O(N*\log(N)\log(N)) O(N∗log(N)log(N));当系统有足够的额外内存时,可缩短为 O ( N ∗ log ( N ) ) O(N*\log(N)) O(N∗log(N))。
算法 stable_sort() 可以保证相等元素的相对顺序,然而 sort() 则不能保证。
如果需要由 partial_sort() 排序的元素数少于元素总数,则其时间复杂性接近 O ( N ) O(N) O(N)。
算法 partial_sort_copy() 的目标必须是一个随机访问迭代器。
算法 nth_element() 只需将升序结果中排在第 n 位的元素放置到正确位置即可(即,之前的元素都不大于它,之后的元素都不小于它)。
| 算法 | 功能 |
|---|---|
| sort(b,e); | 排序[b,e) |
| sort(b,e,f); | 排序[b,e);用f(*p,*q)作为比较标准 |
| stable_sort(b,e); | 排序[b,e);保持相等元素的相对顺序 |
| stable_sort(b,e,f); | 排序[b,e);保持相等元素的相对顺序;用f(*p,*q)作为比较标准 |
| partial_sort(b,m,e); | 部分排序[b,e);令[b,m)有序即可,[m,e)不必有序 |
| partial_sort(b,m,e,f); | 部分排序[b,e);令[b,m)有序即可,[m,e)不必有序;用f(*p,*q)作为比较标准 |
| p = partial_sort_copy(b,e,b2,e2); | 部分排序[b,e);排好前e2-b2(或前e-b)个元素拷贝到[b2,e2);p 为 e2 和 b2 +(e-b) 中的较小者 |
| p = partial_sort_copy(b,eb2,e2,f); | 部分排序[b,e);排好前e2-b2(或前e-b)个元素拷贝到[b2,e2);p 为 e2 和 b2 +(e-b) 中的较小者;用 f 比较元素 |
| is_sort(b,e); | [b,e)已排序? |
| is_sort(b,e,f); | [b,e)已排序?;用 f 比较元素 |
| p = is_sort_until(b,e); | p 指向[b,e)中第一个不符合升序的元素 |
| p = is_sort_until(b,e,f); | p 指向[b,e)中第一个不符合升序的元素;用 f 比较元素 |
| nth_element(b,n,e); | *n的位置恰好是[b,e)排序后它应处的位置;即[b,n)中的元素都<= *n且[n,e)中的元素都>= *n |
| nth_element(b,n,e,f); | *n的位置恰好是[b,e)排序后它应处的位置;即[b,n)中的元素都<= *n且[n,e)中的元素都>= *n;用 f 比较元素 |
| reverse(b,e); | 将[b,e)中的元素逆序排序 |
| p = reverse_copy(b,e,out); | 将[b,e)中的元素逆序拷贝至[out,p) |
二分搜索
binary_serach() 系列算法提供有序序列上的二分搜索。
一旦序列已排序,就可以使用二分搜索查找元素了。
| 算法 | 功能 |
|---|---|
| p = lower_bound(b,e,v); | p 指向[b,e)中 v 首次出现的位置 |
| p = lower_bound(b,e,v,f); | p 指向[b,e)中 v 首次出现的位置;用 f 比较元素 |
| p = upper_bound(b,e,v); | p 指向[b,e)中第一个大于 v 的元素 |
| p = upper_bound(b,e,v,f); | p 指向[b,e)中第一个大于 v 的元素;用 f 比较元素 |
| binary_search(b,e,v); | v 在有序序列[b,e)中吗? |
| binary_search(b,e,v,f); | v 在有序序列[b,e)中吗?;用 f 比较元素 |
| pair(p1,p2) = equal_range(b,e,v); | [p1,p2)是[b,e)中值为 v 的子序列;通常用二分搜索查找 v |
| pair(p1,p2) = equal_range(b,e,v,f); | [p1,p2)是[b,e)中值为 v 的子序列;通常用二分搜索查找 v;用 f 比较元素 |
merge()
算法 merge() 将两个有序序列合并为一个序列。
算法 merge() 可以接受不同类别的序列和不同类型的元素。
| 算法 | 功能 |
|---|---|
| p = merge(b,e,b2,e2,out); | 合并两个有序序列[p1,p2)与[b,e),结果写入[out,p) |
| p = merge(b,e,b2,e2,out,f); | 合并两个有序序列[p1,p2)与[b,e),结果写入[out,out+p);用 f 比较元素 |
| inplace_merge(b,m,e); | 原址合并;将两个有序子序列[b,m)与[m,e)合并为有序序列[b,e) |
| inplace_merge(b,m,e,f); | 原址合并;将两个有序子序列[b,m)与[m,e)合并为有序序列[b,e);用 f 比较元素 |
集合算法
这些算法将序列当作一个元素集合来处理,并提供基本的集合操作。
输入序列应是排好序的,输出序列也会被排序。
| 算法 | 功能 |
|---|---|
| includes(b,e,b2,e2); | [b,e)中的所有元素也都在[b2,e2)中? |
| includes(b,e,b2,e2,f); | [b,e)中的所有元素也都在[b2,e2)中?用 f 比较元素 |
| p = set_union(b,e,b2,e2,out); | 创建一个有序序列[out,p) ,包含[b,e)和[b2,e2)中的所有元素 |
| p = set_union(b,e,b2,e2,out,f); | 创建一个有序序列[out,p) ,包含[b,e)和[b2,e2)中的所有元素;用 f 比较元素 |
| p = set_intersection(b,e,b2,e2,out); | 创建一个有序序列[out,p) ,包含[b,e)和[b2,e2)中共同的元素 |
| p = set_intersection(b,e,b2,e2,out,f); | 创建一个有序序列[out,p) ,包含[b,e)和[b2,e2)中共同的元素;用 f 比较元素 |
| p = set_difference(b,e,b2,e2,out); | 创建一个有序序列[out,p) ,其元素在[b,e)中但不在[b2,e2)中 |
| p = set_difference(b,e,b2,e2,out,f); | 创建一个有序序列[out,p) ,其元素在[b,e)中但不在[b2,e2)中;用 f 比较元素 |
| p = set_symmetric_difference(b,e,b2,e2,out); | 创建一个有序序列[out,p) ,其元素在[b,e)中或在[b2,e2)中,但不同时在两者中 |
| p = set_symmetric_difference(b,e,b2,e2,out,f); | 创建一个有序序列[out,p) ,其元素在[b,e)中或在[b2,e2)中,但不同时在两者中;用 f 比较元素 |
堆
堆是一种按最大值优先的方式组织元素的紧凑数据结构。
堆算法允许将一个随机访问序列作为堆处理。
堆的关键特点是提供了快速插入新元素和快速访问最大元素的能力;其主要用途是实现优先队列。
| 算法 | 功能 |
|---|---|
| make_heap(b,e); | 将[b,e)整理为一个堆 |
| make_heap(b,e,f); | 将[b,e)整理为一个堆;用 f 比较元素 |
| push_heap(b,e); | 将*(e-1)添加到堆[b,e-1)中,使得[b,e)还是一个堆 |
| push_heap(b,e,f); | 将*(e-1)添加到堆[b,e-1)中,使得[b,e)还是一个堆;用 f 比较元素 |
| pop_heap(b,e); | 从堆[b,e)中删除最大值(*b与*(e-1)交换后删除*(e-1)),[b,e-1)保持堆结构 |
| pop_heap(b,e,f); | 从堆[b,e)中删除最大值(*b与*(e-1)交换后删除*(e-1)),[b,e-1)保持堆结构;用 f 比较元素 |
| sort_heap(b,e); | 排序堆[b,e) |
| sort_heap(b,e,f); | 排序堆[b,e);用 f 比较元素 |
| is_heap(b,e); | [b,e)是一个堆吗? |
| is_heap(b,e,f); | [b,e)是一个堆吗?用 f 比较元素 |
| p = is_heap_until(b,e); | p 是满足[b,p)堆的最大位置 |
| p = is_heap_until(b,e,f); | p 是满足[b,p)堆的最大位置;用 f 比较元素 |
lexicographical_compare()
字典序比较就是我们用来排序字典中单词的规则。
| 算法 | 功能 |
|---|---|
| lexicographical_compare(b,e,b2,e2); | [b,e) < [b2,e2)? |
| lexicographical_compare(b,e,b2,e2,f); | [b,e) < [b2,e2)?用 f 比较元素 |
最大值和最小值
如果比较两个左值,返回的是指向结果的引用;否则,返回一个右值。
但是,接受左值的版本接受的是 const 左值,因此永远也不能修改这些函数的返回结果。
| 算法 | 功能 |
|---|---|
| x = min(a,b); | x 是 a 和 b 中的较小者 |
| x = min(a,b,f); | x 是 a 和 b 中的较小者,用 f 比较元素 |
| x = min({elem}); | x 是 {elem} 中的最小元素 |
| x = min({elem},f); | x 是 {elem} 中的最小元素,用 f 比较元素 |
| x = max(a,b); | x 是 a 和 b 中的较大者 |
| x = max(a,b,f); | x 是 a 和 b 中的较大者,用 f 比较元素 |
| x = max({elem}); | x 是 {elem} 中的最大元素 |
| x = max({elem},f); | x 是 {elem} 中的最大元素,用 f 比较元素 |
| pair(x,y) = minmax(a,b); | x 为 min(a,b),y 为 max(a,b) |
| pair(x,y) = minmax(a,b,f); | x 为 min(a,b,f),y 为 max(a,b,f) |
| pair(x,y) = minmax({elem}); | x 为 min({elem}),y 为 max({elem}) |
| pair(x,y) = minmax({elem},f); | x 为 min({elem},f),y 为 max({elem},f) |
| p = min_element(b,e); | p 指向[b,e)中的最小元素或 e |
| p = min_element(b,e,f); | p 指向[b,e)中的最小元素或 e,用 f 比较元素 |
| p = max_element(b,e); | p 指向[b,e)中的最大元素或 e |
| p = max_element(b,e,f); | p 指向[b,e)中的最大元素或 e,用 f 比较元素 |
| pair(x,y) = minmax_element(b,e); | x 为 min_element(b,e),y 为 max_element(b,e) |
| pair(x,y) = minmax_element(b,e,f); | x 为 min_element(b,e,f),y 为 max_element(b,e,f) |
相关文章:

C++ STL泛型算法
泛型算法 <algorithm>定义了大约 80 个标准算法。 它们操作由一对迭代器定义的(输入)序列或单一迭代器定义的(输出)序列。 当对两个序列进行拷贝、比较操作时,第一个序列由一对迭代器[b,e)表示,但第…...

使用OpenSSL生成PKCS#12格式的证书和私钥
要使用OpenSSL生成PKCS12格式的证书和私钥,可以按照以下步骤进行操作: 1. 安装OpenSSL 首先,确保已在计算机上安装了OpenSSL。可以从OpenSSL官方网站(https://www.openssl.org/)下载并安装适用于您的操作系统的版本。…...
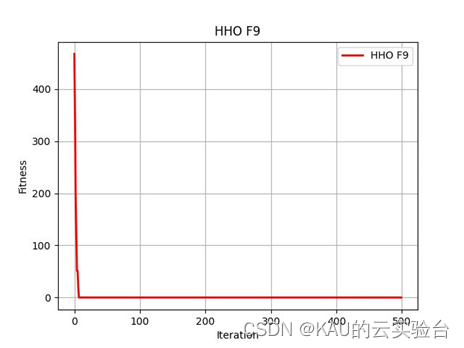
超详细 | 哈里斯鹰优化算法原理、实现及其改进与利用(Matlab/Python)
测试函数为F9 在MATLAB中执行程序结果如下: 在Python中执行程序结果如下: 哈里斯鹰优化算法(Harris Hawks Optimization , HHO)是 Heidari等[1]于2019年提出的一种新型元启发式算法,设计灵感来源于哈里斯鹰在捕食猎物过程中的合作行为以及突…...

git 切换远程地址分支 推送到指定地址分支 版本回退
切换远程地址 1、切换远程仓库地址: 方式一:修改远程仓库地址 【git remote set-url origin URL】 更换远程仓库地址,URL为新地址。 git remote set-url https://gitee.com/xxss/omj_gateway.git 方式二:先删除远程仓库地址&…...

YOLOv3-YOLOv8的一些总结
0 写在前面 这个文档主要总结YOLO系列的创新点,以YOLOv3为baseline。参考(抄)了不少博客,就自己看看吧。有些模型的trick不感兴趣就没写进来,核心的都写了。 YOLO系列的网络都由四个部分组成:Input、Backbone、Neck、Prediction…...

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)控件的部分公共属性和事件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)控件的部分公共属性和事件 一、操作环境 操作系统: Windows 10 专业版 IDE:DevEco Studio 3.1 SDK:HarmonyOS 3.1 二、公共属性 常用的公共属性有: 宽(with)、高(height)、…...
最新同步云盘推荐:实现轻松管理与便捷同步的理想选择
同步云盘——可以轻松管理文件,同步不同设备之间的文件,受到了许多用户的青睐!目前国内有什么值得推荐的同步云盘? Zoho Workdrive同步云盘,助您轻松管理文件,进行多设备同步,便捷使用文件&…...
Oracle 数据泵转换分区表)
(第27天)Oracle 数据泵转换分区表
在Oracle数据库中,分区表的使用是很常见的,使用数据泵也可以进行普通表到分区表的转换,虽然实际场景应用的不多。 创建测试表 sys@ORADB 2022-10-13 11:54:12> create table lucifer.tabs as select * from dba_objects;Table created.sys...

业务上需要顺序消费,怎么保证时序性?
消息传输和消费的有序性,是消息队列应用中一个非常重要的问题,在分布式系统中,很多业务场景都需要考虑消息投递的时序。例如,电商中的订单状态流转、数据库的 binlog 分发,都会对业务的有序性有要求。今天我们一起来看…...
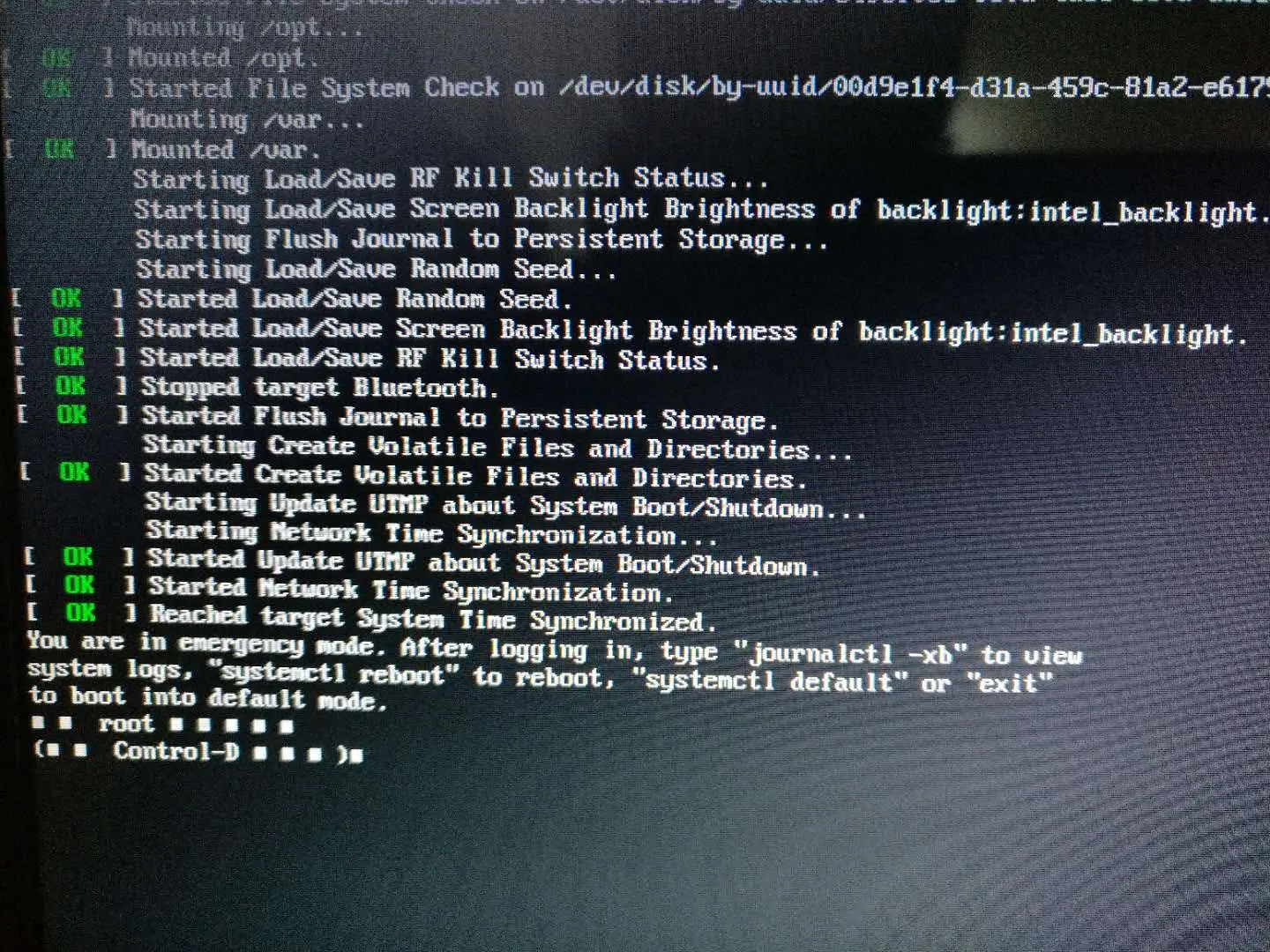
ubuntu 开机提示 you are in emergency mode,journalctl -xb
进入系统界面 回车输入: journalctl -xb -p3 查看出问题的盘符类型。 然后 lsblk 查看挂载情况 我的是/dev/sda3没有挂载上,对应/home目录,注意这时候不要直接mount 需要先修复 fsck -y /dev/sda3等待修复完成,在重新挂载 moun…...
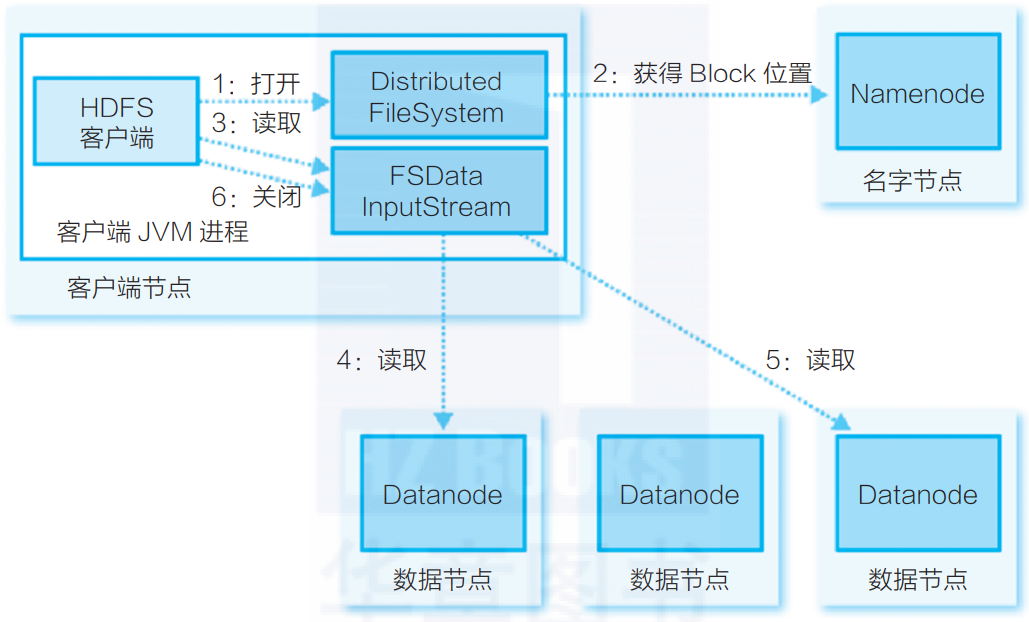
【Hadoop面试】HDFS读写流程
HDFS(Hadoop Distributed File System)是GFS的开源实现。 HDFS架构 HDFS是一个典型的主/备(Master/Slave)架构的分布式系统,由一个名字节点Namenode(Master) 多个数据节点Datanode(Slave)组成。其中Namenode提供元数…...
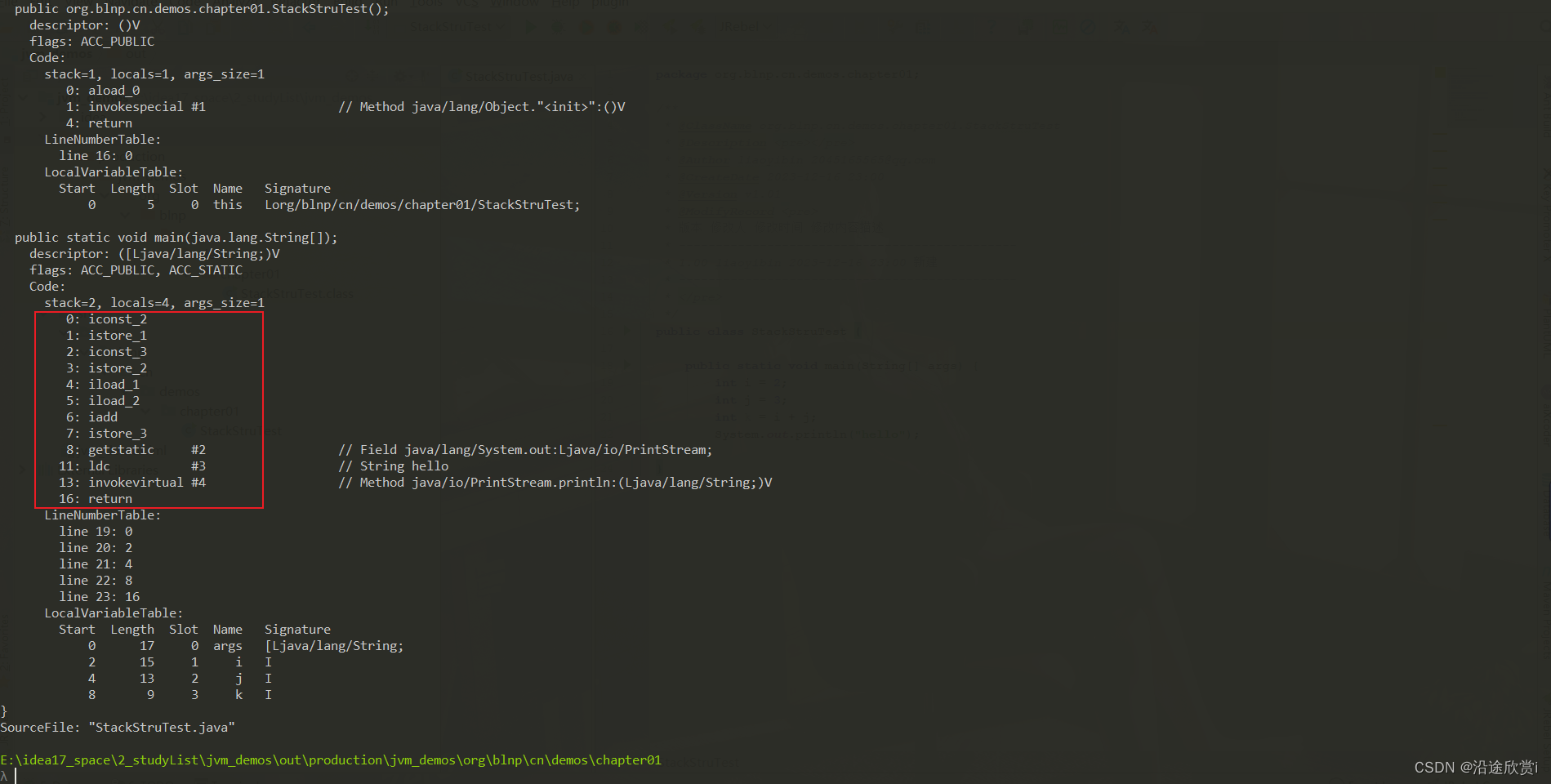
B01、JVM与Java体系结构-01
字节码与多语言混合编程 字节码概述: 我们平时说的java字节码,指的是用java语言编译成的字节码。准确的说任何能在jvm平台上执行的字节码格式都是一样的。所以应该统称为:jvm字节码。不同的编译器,可以编译出相同的字节码文件&…...

Python:Jupyter
Jupyter是一个开源的交互式计算环境,由Fernando Perez和Brian Granger于2014年创立。它提供了一种方便的方式来展示、共享和探索数据,并且可以与多种编程语言和数据格式进行交互。Jupyter的历史可以追溯到2001年,当时Fernando Perez正在使用P…...

macos苹果电脑开启tftp server上传fortigate60e固件成功
cat /System/Library/LaunchDaemons/tftp.plist<?xml version"1.0" encoding"UTF-8"?> <!DOCTYPE plist PUBLIC "-//Apple Computer//DTD PLIST 1.0//EN" "http://www.apple.com/DTDs/PropertyList-1.0.dtd"> <plist…...
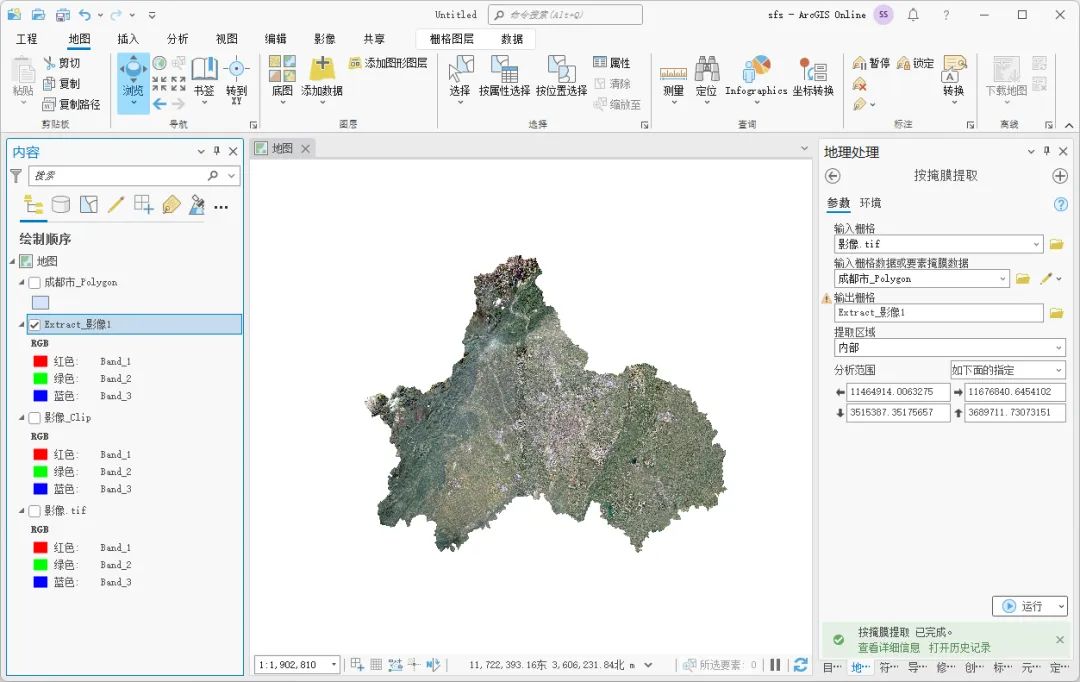
如何使用ArcGIS Pro裁剪影像
对影像进行裁剪是一项比较常规的操作,因为到手的影像可能是多种范围,需要根据自己需求进行裁剪,这里为大家介绍一下ArcGIS Pro中裁剪的方法,希望能对你有所帮助。 数据来源 本教程所使用的数据是从水经微图中下载的影像和行政区…...
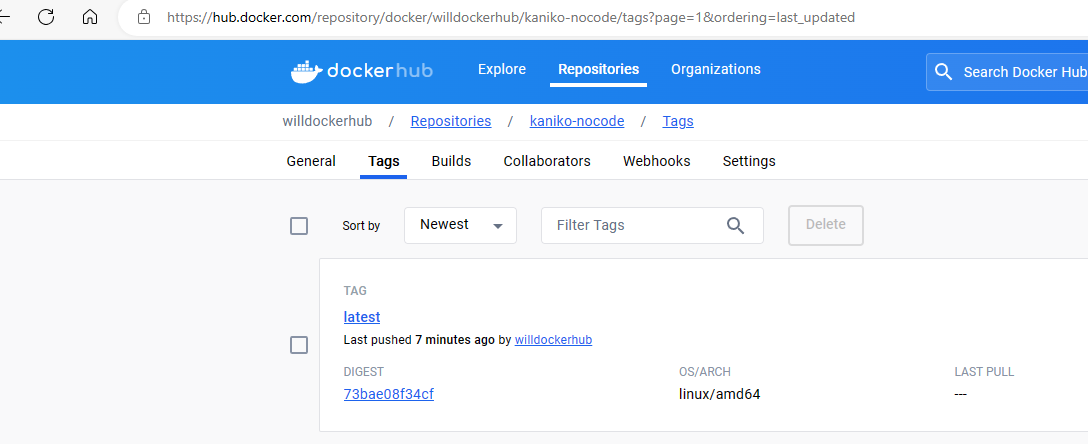
Tekton 构建容器镜像
Tekton 构建容器镜像 介绍如何使用 Tektonhub 官方 kaniko task 构建docker镜像,并推送到远程dockerhub镜像仓库。 kaniko task yaml文件下载地址:https://hub.tekton.dev/tekton/task/kaniko 查看kaniko task yaml内容: 点击Install&…...

netty-daxin-4(httpwebsocket)
文章目录 学习链接http服务端NettyHttpServerHelloWorldServerHandler 客户端ApiPost websocket初步了解为什么需要 WebSocket简介 浏览器的WebSocket客户端客户端的简单示例客户端的 APIWebSocket 构造函数webSocket.readyStatewebSocket.onopenwebSocket.onclosewebSocket.ο…...

文章解读与仿真程序复现思路——电力系统自动化EI\CSCD\北大核心《市场环境下考虑全周期经济效益的工业园区共享储能优化配置》
这个标题涉及到工业园区中共享储能系统的优化配置,考虑了市场环境和全周期经济效益。以下是对标题中各个要素的解读: 市场环境下: 指的是工业园区所处的商业和经济背景。这可能包括市场竞争状况、电力市场价格波动、政策法规等因素。在这一环…...
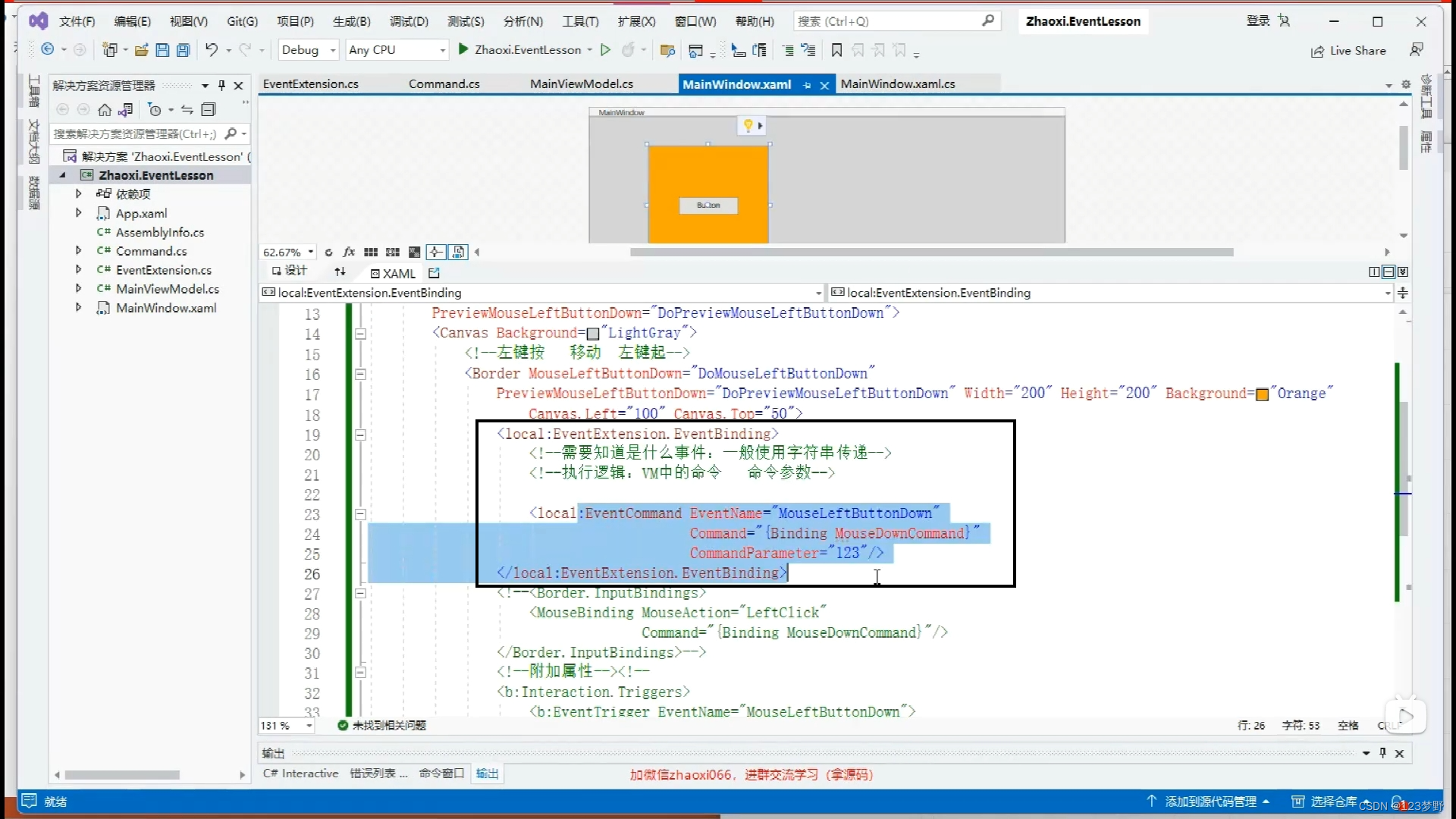
WPF——命令commond的实现方法
命令commond的实现方法 属性通知的方式 鼠标监听绑定事件 行为:可以传递界面控件的参数 第一种: 第二种: 附加属性 propa:附加属性快捷方式...
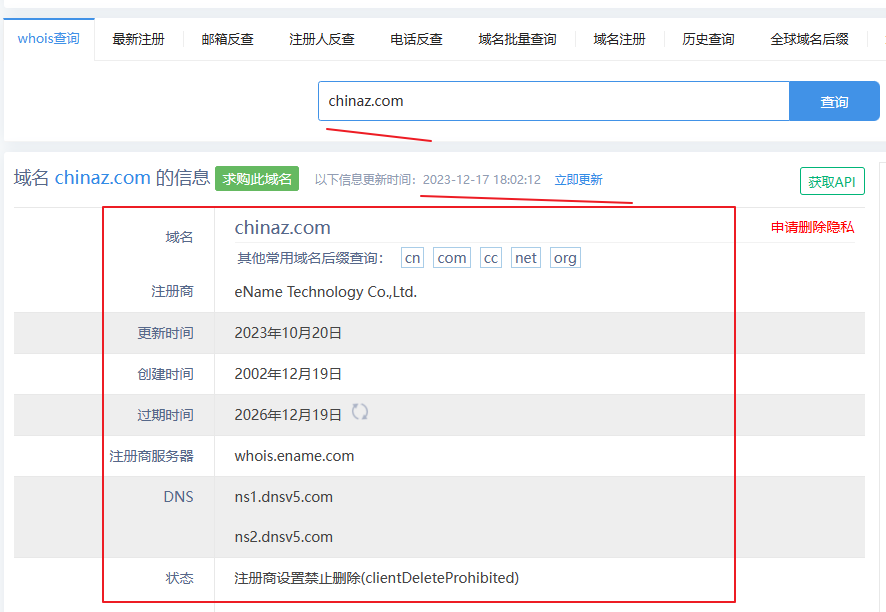
信息收集 - 域名
1、Whois查询: Whois 是一个用来查询域名是否已经被注册以及相关详细信息的数据库(如:域名所有人、域名注册商、域名注册日期和过期日期等)。通过访问 Whois 服务器,你可以查询域名的归属者联系方式和注册时间。 你可以在 域名Whois查询 - 站长之家 上进行在线查询。 2、…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
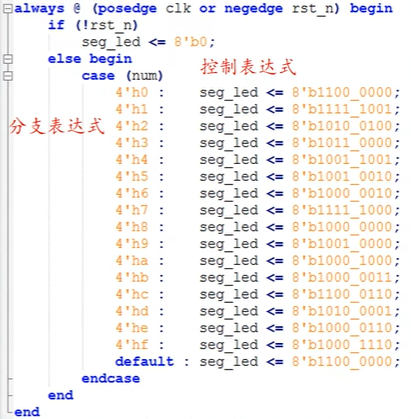
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...

更新 Docker 容器中的某一个文件
🔄 如何更新 Docker 容器中的某一个文件 以下是几种在 Docker 中更新单个文件的常用方法,适用于不同场景。 ✅ 方法一:使用 docker cp 拷贝文件到容器中(最简单) 🧰 命令格式: docker cp <…...
