Bezier 曲线 2D
Bezier 曲线于 1962 年由法国雪铁龙汽车公司的工程师 Bezier 所发表,主要应用于汽车的外形设计。虽然 Bezier 曲线早在 1959 年便由法国雷诺汽车公司的 De Casteljau 运用递推算法开发成功,但是 Bezier 却给出了曲线的详细的曲线计算公式。所以,命名为 Bezier 曲线.
Bezier 曲线由控制多边形唯一定义。
控制多边形的第一个顶点和最后一个顶点位于曲线上,多边形的第一条边和最后一条边表示了曲线在起点和终点的切矢量方向,其顶点则用于定义曲线的导数,阶次和形状。曲线的形状趋近于控制多边形并位于多边形所构成的土包内,改变控制多边形的顶点位置就会改变曲线的形状。
Bezier 曲线的直观交互性使得对设计对象的逼近达到了直接的集合化程度,使得起来非常方便。
Bezier 曲线的定义
给定 n + 1 n+1 n+1 个控制点 P i ( i = 0 , 1 , 2 , ⋯ n ) P_i (i=0, 1, 2, \cdots n) Pi(i=0,1,2,⋯n),则 n n n次Bezier 曲线的定义为
P ( t ) = ∑ i = 0 n P i B i , n ( t ) , t ∈ [ 0 , 1 ] P(t) = \sum_{i=0}{n}P_i B_{i, n}(t), t\in[0, 1] P(t)=∑i=0nPiBi,n(t),t∈[0,1]
P i ( i = 0 , 1 , 2 , ⋯ , n ) P_i(i=0, 1, 2, \cdots, n) Pi(i=0,1,2,⋯,n) 是控制多边形的 n + 1 n+1 n+1 个控制点. B i , n ( t ) B_{i, n}(t) Bi,n(t)是 Bernstein 基函数,其表达式为
B i , n ( t ) = n ! i ! ( n − i ) ! t i ( 1 − t ) n − i = C n i t i ( 1 − t ) n − i , i = 0 , 1 , 2 , ⋯ n \begin{equation} B_{i, n}(t) = \frac{n!}{i!(n-i)!}t^{i}(1-t)^{n-i} = C_{n}^{i}t^{i}(1-t)^{n-i}, \quad i=0, 1, 2, \cdots n \end{equation} Bi,n(t)=i!(n−i)!n!ti(1−t)n−i=Cniti(1−t)n−i,i=0,1,2,⋯n
Bezier 函数是控制点关于 Bernstein 基函数的加权和,Bezier 曲线的次数为 n , 需要 n+1 个顶点来定义。
在工程项目中,最常见的是三次Bezier 曲线,其次数是二次Bezier 曲线,高次Bezier 曲线一般很少用
一次 Bezier 曲线, 当 n=1 时,Bezier 曲线的控制多边形有两个控制点 P 0 P_0 P0 和 P 1 P_1 P1, Bezier 曲线是一次多项式,称为一次 Bezier 曲线,
P ( t ) = ∑ i = 0 1 P i B i , 1 ( t ) = ( 1 − t ) P 0 + t P 1 P(t) = \sum_{i=0}^{1}P_i B_{i, 1}(t) = (1-t)P_0 + tP_{1} P(t)=i=0∑1PiBi,1(t)=(1−t)P0+tP1
二次 Bezier 曲线,当 n=2 时,Bezier 曲线的控制多边形有 3 个控制点, KaTeX parse error: Expected group after '_' at position 2: P_̲$ 、 P 1 P_1 P1和 P 2 P_2 P2, Bezier 曲线是二次多项式,称为二次 Bezier 曲线,
P ( t ) = ∑ i = 0 2 P i B i , 2 ( t ) = ( 1 − t ) 2 P 0 + 2 t ( 1 − t ) P 1 + t 2 P 2 P(t) = \sum_{i=0}^{2}P_i B_{i, 2}(t) = (1-t)^2P_0 + 2t(1-t)P_{1} + t^2P_2 P(t)=i=0∑2PiBi,2(t)=(1−t)2P0+2t(1−t)P1+t2P2
三次 Bezier 曲线,当 n=3 时,Bezier 曲线控制多边形有 4 个控制点, P 0 P_0 P0 、 P 1 P_1 P1、 P 2 P_2 P2 和 P 3 P_3 P3, Bezier 曲线是三次多项式,称为三次 Bezier 曲线
P ( t ) = ∑ i = 0 3 P i B i , 3 ( t ) = ( 1 − t ) 3 P 0 + 3 t ( 1 − t ) 2 P 1 + 3 t 2 ( 1 − t ) P 2 + t 3 P 3 = ( − t 3 + 3 t 2 − 3 t + 1 ) P 0 + ( 3 t 3 − 6 t 2 + 3 t ) P 1 + ( − 3 t 3 + 3 t 2 ) P 2 + t 3 P 3 P(t) = \sum_{i=0}^{3}P_i B_{i, 3}(t) = (1-t)^3 P_0 + 3t(1-t)^2P_{1} + 3t^2(1-t)P_2 + t^3P_3 = (-t^3 + 3t^2 -3t+1)P_0 + (3t^3 -6t^2 + 3t)P_1 + (-3t^3+3t^2)P_2 + t^3P_3 P(t)=i=0∑3PiBi,3(t)=(1−t)3P0+3t(1−t)2P1+3t2(1−t)P2+t3P3=(−t3+3t2−3t+1)P0+(3t3−6t2+3t)P1+(−3t3+3t2)P2+t3P3
写成矩阵的形式为
P ( t ) = [ t 3 t 2 t 1 ] [ − 1 3 − 3 1 3 − 6 3 0 − 3 3 0 0 1 0 0 0 ] [ P 0 P 1 P 2 P 3 ] P(t) = \begin{bmatrix} t^3 & t^2 & t & 1 \end{bmatrix} \begin{bmatrix} -1 & 3 &-3 & 1\\ 3 & -6 &3 & 0\\ -3 & 3 &0 & 0\\ 1 & 0 & 0 & 0\\ \end{bmatrix} \begin{bmatrix} P_0 \\ P_1 \\ P_2 \\ P_3 \\ \end{bmatrix} P(t)=[t3t2t1] −13−313−630−33001000 P0P1P2P3
B 0 , 3 ( t ) = ( 1 − t ) 3 B 1 , 3 ( t ) = 3 t ( 1 − t ) 2 B 2 , 3 ( t ) = 3 t 2 ( 1 − t ) B 3 , 3 ( t ) = t 3 B_{0, 3}(t) = (1-t)^3 \\ B_{1, 3}(t) = 3t(1-t)^2 \\ B_{2, 3}(t) = 3t^2(1-t) \\ B_{3, 3}(t) = t^3 B0,3(t)=(1−t)3B1,3(t)=3t(1−t)2B2,3(t)=3t2(1−t)B3,3(t)=t3
下面给出 QT + OPENGL 的二次的代码
#include <QtWidgets>
#include <QOpenGLWidget>
#include <QOpenGLFunctions>class BezierCurveWidget : public QOpenGLWidget, protected QOpenGLFunctions {
public:BezierCurveWidget(QWidget* parent = nullptr): QOpenGLWidget(parent) {}protected:void initializeGL() override {initializeOpenGLFunctions();glClearColor(1.0f, 1.0f, 1.0f, 1.0f);}void resizeGL(int w, int h) override {glViewport(0, 0, w, h);glMatrixMode(GL_PROJECTION);glLoadIdentity();glOrtho(0, w, h, 0, -1, 1);glMatrixMode(GL_MODELVIEW);}void paintGL() override {glClear(GL_COLOR_BUFFER_BIT);// 控制点坐标QPoint p0(100, 300);QPoint p1(300, 100);QPoint p2(500, 300);// 设置线的颜色glColor3f(0.0f, 0.0f, 1.0f); // Blue color for lines// 绘制Bezier曲线glBegin(GL_LINE_STRIP);for (float t = 0.0f; t <= 1.0f; t += 0.01f) {QPoint p = calculateBezierPoint(t, p0, p1, p2);glVertex2i(p.x(), p.y());}glEnd();// 绘制控制点glPointSize(5.0f);glColor3f(1.0f, 0.0f, 0.0f);glBegin(GL_POINTS);glVertex2i(p0.x(), p0.y());glVertex2i(p1.x(), p1.y());glVertex2i(p2.x(), p2.y());glEnd();// 绘制连接线glBegin(GL_LINES);glVertex2i(p0.x(), p0.y());glVertex2i(p1.x(), p1.y());glVertex2i(p1.x(), p1.y());glVertex2i(p2.x(), p2.y());glEnd();}QPoint calculateBezierPoint(float t, const QPoint& p0, const QPoint& p1, const QPoint& p2) {float u = 1 - t;float tt = t * t;float uu = u * u;float x = uu * p0.x() + 2 * u * t * p1.x() + tt * p2.x();float y = uu * p0.y() + 2 * u * t * p1.y() + tt * p2.y();return QPoint(x, y);}
};int main(int argc, char *argv[]) {QApplication a(argc, argv);QMainWindow window;BezierCurveWidget* bezierWidget = new BezierCurveWidget(&window);window.setCentralWidget(bezierWidget);window.resize(600, 400);window.show();return a.exec();
}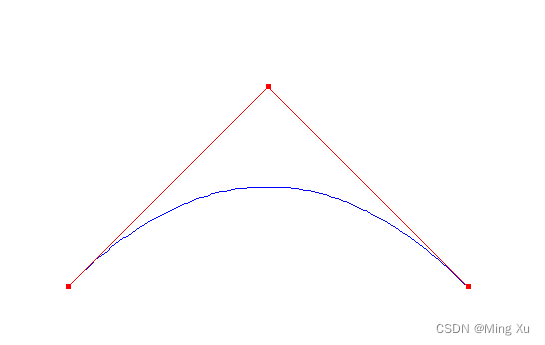
这里只需要替换一次和三次的计算部分即可。
相关文章:

Bezier 曲线 2D
Bezier 曲线于 1962 年由法国雪铁龙汽车公司的工程师 Bezier 所发表,主要应用于汽车的外形设计。虽然 Bezier 曲线早在 1959 年便由法国雷诺汽车公司的 De Casteljau 运用递推算法开发成功,但是 Bezier 却给出了曲线的详细的曲线计算公式。所以ÿ…...
Linux静态ip
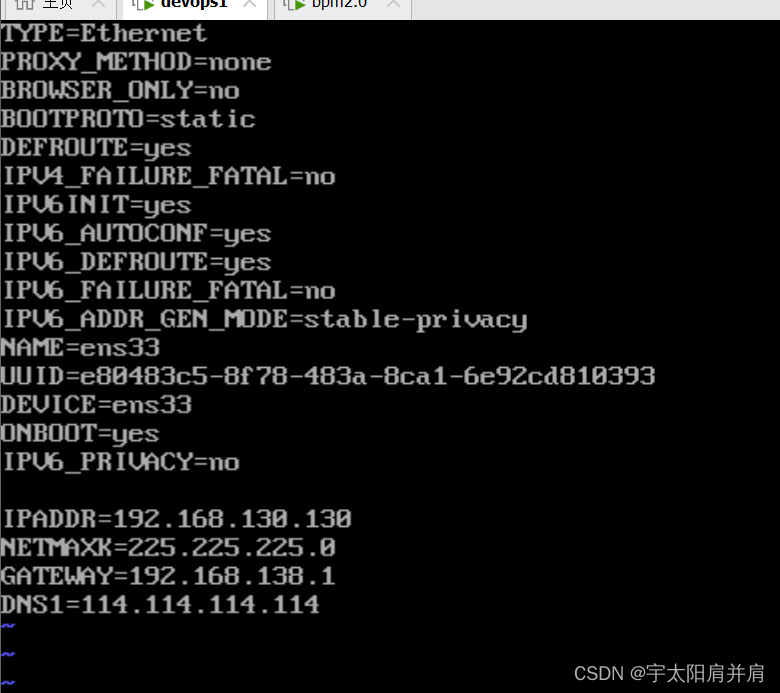
Linux静态ip Ⅰ、修改静态ip Ⅰ、修改静态ip 修改静态ip必须是root用户 su root //切换root用户 ip a //查看修改前的动态ipvi /etc/sysconfig/network-scripts/ifcfg-ens33 //打开网卡配置文件,修改一处,新增四处 BOOTPROTO&quo…...
一种基于外观-运动语义表示一致性的视频异常检测框架 论文阅读
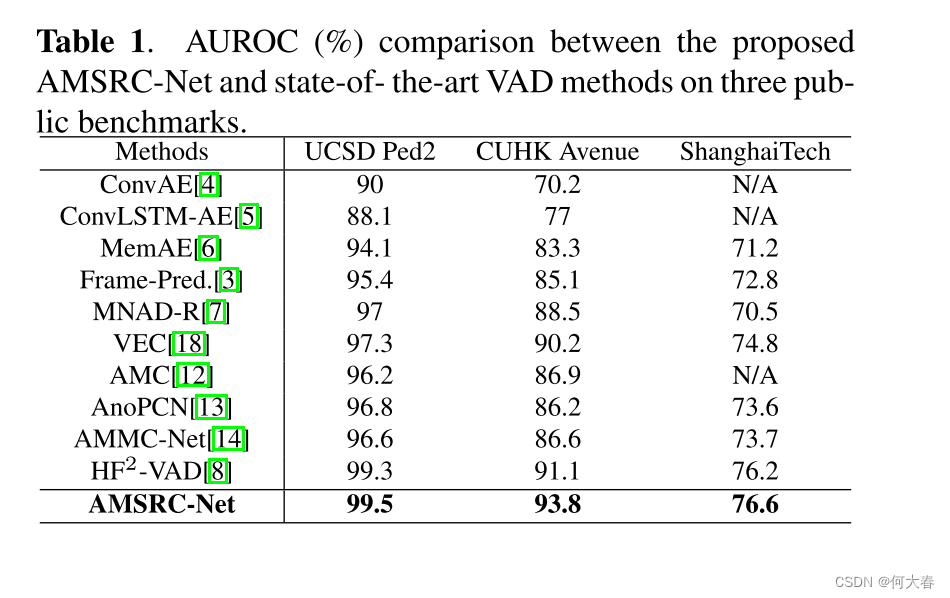
A VIDEO ANOMALY DETECTION FRAMEWORK BASED ON APPEARANCE-MOTION SEMANTICS REPRESENTATION CONSISTENCY 论文阅读 ABSTRACT1. INTRODUCTION2. PROPOSED METHOD3. EXPERIMENTAL RESULTS4. CONCLUSION阅读总结: 论文标题:A VIDEO ANOMALY DETECTION FRA…...

Netty—NIO万字详解
文章目录 NIO基本介绍同步、异步、阻塞、非阻塞IO的分类NIO 和 BIO 的比较NIO 三大核心原理示意图NIO的多路复用说明 核心一:缓存区 (Buffer)Buffer类及其子类Buffer缓冲区的分类MappedByteBuffer类说明: 核心二:通道 (Channel)Channel类及其…...
)
面试经典150题(32-37)
leetcode 150道题 计划花两个月时候刷完,今天(第十五天)完成了6道(32-37)150: 今天刚好有点没精神的感觉,然后碰到的题也不难。。天意!!! 32.(289. 生命游戏࿰…...

手撕分布式缓存---HTTP Client搭建
经过上个章节的学习,我们已经实现了一致性哈希算法,这个算法保证我们可以在节点发生变动时,最少的key请求受到影响,并返回这个节点的名称;这很大程度上避免了哈希雪崩和哈希穿透的问题。这个章节我们要基于此实现完整的…...

word如何快速制作简易代码块
先上解决方案。 方式一(全自动): typora编辑,导出选择word文档即可。内网环境,故放弃。 方式二(全手动): 在修改文档时,左侧会有“段落布局”按钮,点击该按…...

Linux常用网络指令
网络参数设定使用的指令 手动/自动设定与启动/关闭 IP 参数:ifconfig, ifup, ifdown ifconfig ifconfig常用于修改网络配置以及查看网络参数的指令 [rootwww ~]# ifconfig {interface} {up|down} < 观察与启动接口 [rootwww ~]# ifconfig interface {options…...
)
Spark on Yarn 安装配置实验(3.1.1)
子任务二: Spark on Yarn 安装配置 本任务需要使用 root 用户完成相关配置, 已安装 Hadoop 及需要配置前置环境,具体要求如下: 1 、从宿主机 /opt 目录下将文件 spark-3.1.1-bin-hadoop3.2.tgz 复制到容器 Master 中的 /opt/software (若 路径不存在,则需新…...
详解YOLOv5网络结构/数据集获取/环境搭建/训练/推理/验证/导出/部署
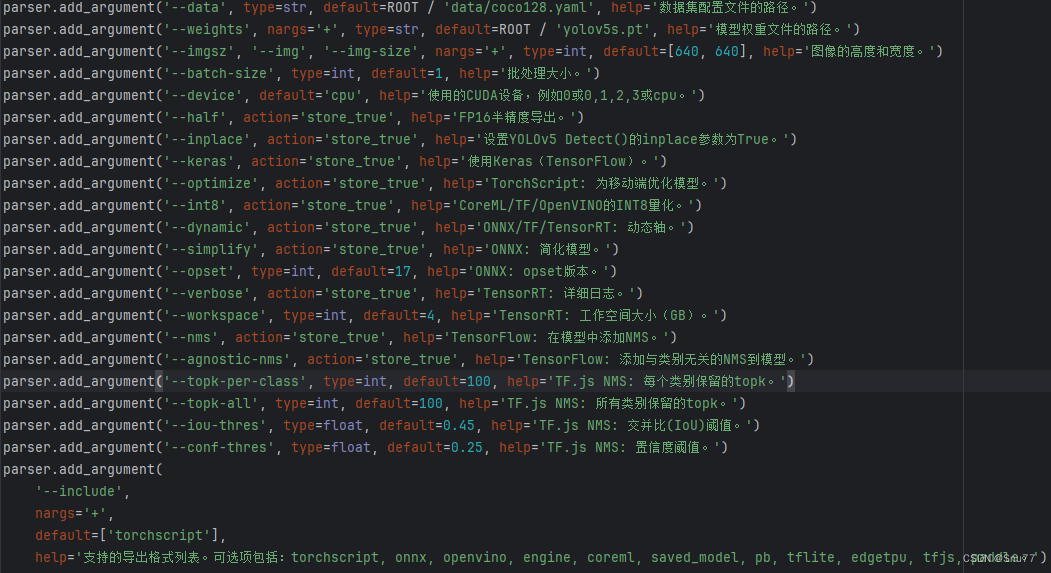
一、本文介绍 本文给大家带来的教程是利用YOLOv5训练自己的数据集,以及有关YOLOv5的网络结构讲解/数据集获取/环境搭建/训练/推理/验证/导出/部署相关的教程,同时通过示例的方式让大家来了解具体的操作流程,过程中还分享给大家一些好用的资源…...

ansible(不能交互)
1、定义 基于python开发的一个配置管理和应用部署工具,在自动化运维中异军突起,类似于xshell一键输入的工具,不需要每次都切换主机进行操作,只要有一台ansible的固定主机,就可以实现所有节点的操作。不需要agent客户端…...
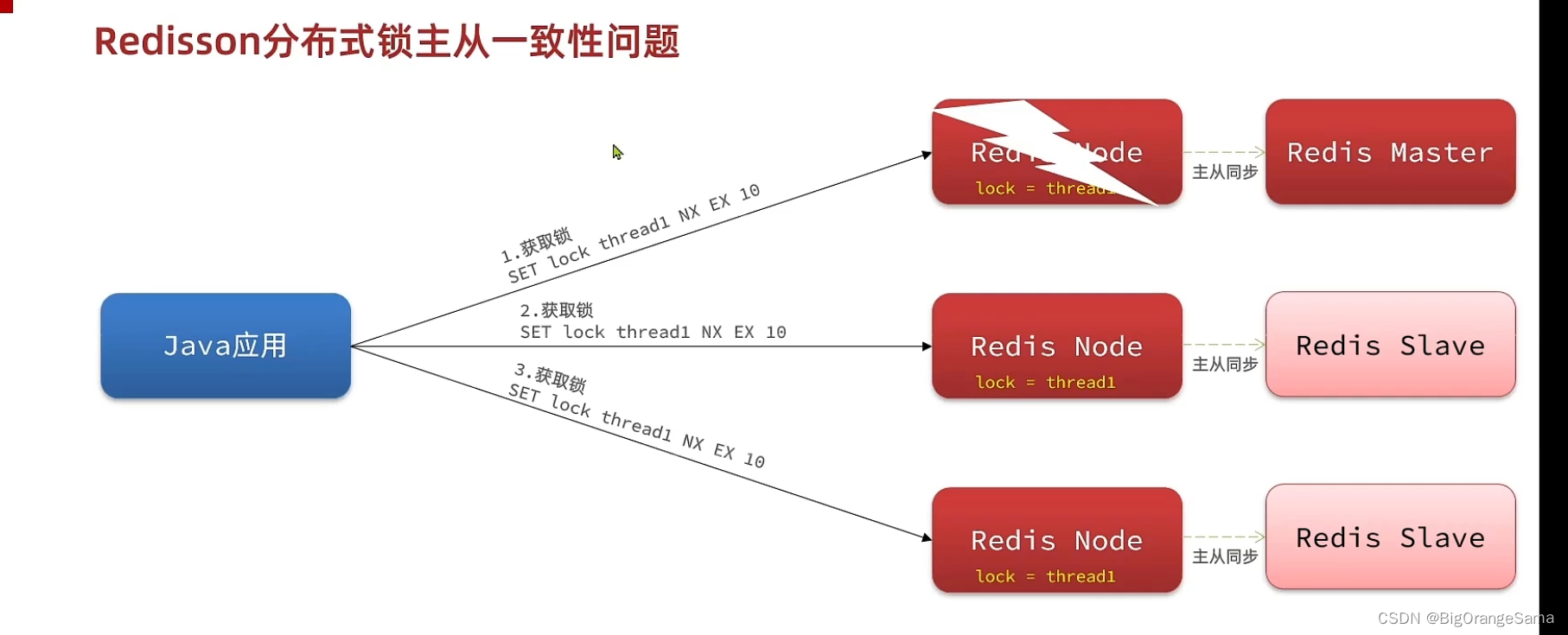
黑马点评06分布式锁 2Redisson
实战篇-17.分布式锁-Redisson功能介绍_哔哩哔哩_bilibili 1.还存在的问题 直接实现很麻烦,借鉴已有的框架。 2.Redisson用法 3.Redisson可重入原理 在获取锁的时候,看看申请的线程和拿锁的线程是否一致,然后计算该线程获取锁的次数。一个方法…...

深度剖析知识图谱:方法、工具与实战案例
💂 个人网站:【 海拥】【神级代码资源网站】【办公神器】🤟 基于Web端打造的:👉轻量化工具创作平台💅 想寻找共同学习交流的小伙伴,请点击【全栈技术交流群】 知识图谱作为一种强大的知识表示和关联技术&am…...

Oracle中的dblink简介
Oracle中的dblink简介 是一种用于在不同数据库之间进行通信和数据传输的工具。它允许用户在一个数据库中访问另一个数据库中的对象,而无需在本地数据库中创建这些对象。 使用dblink,用户可以在一个数据库中执行SQL语句,然后访问另一个数据库中…...
ubuntu安装显卡驱动过程中遇到的错误,及解决办法!
ubuntu安装显卡驱动的过程中,可能会遇到以下问题,可以参考解决办法! 问题1: ERROR: An error occurred while performing the step: "Building kernel modules". See /var/log/nvidia-installer.log for details. …...
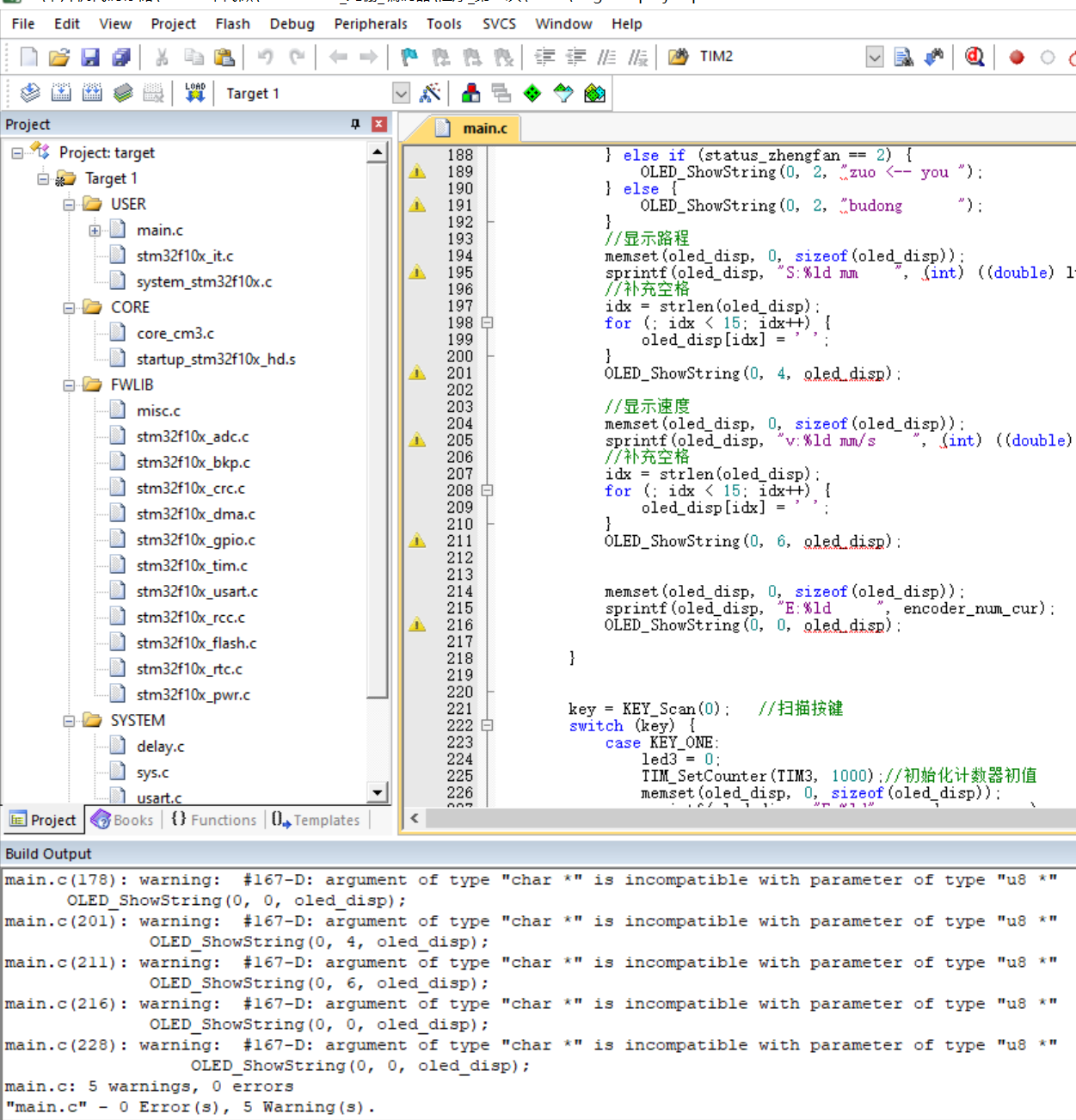
【程序】STM32 读取光栅_编码器_光栅传感器_7针OLED
文章目录 源代码工程编码器基础程序参考资料 源代码工程 源代码工程打开获取: http://dt2.8tupian.net/2/28880a55b6666.pg3这里做了四倍细分,在屏幕上显示 速度、路程、方向。 接线方法: 单片机--------------串口模块 单片机的5V-------…...
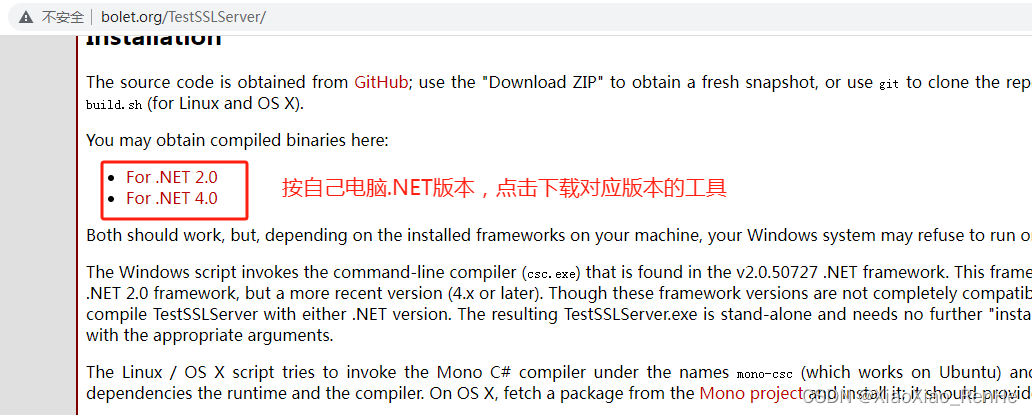
TestSSLServer4.exe工具使用方法简单介绍(查SSL的加密版本SSL3或是TLS1.2)
一、工具使用方法介绍 工具使用方法参照:http://www.bolet.org/TestSSLServer/ 全篇英文看不懂,翻译了下,能用到的简单介绍如下: 将下载的TestSSLServer4.exe工具放到桌面上,CMD命令行进入到桌面目录,执…...

新年跨年烟花超酷炫合集【内含十八个烟花酷炫效果源码】
❤️以下展示为全部烟花特效效果 ❤️下方仅展示部分代码 ❤️源码获取见文末 🎀HTML5烟花喷泉 <style> * {padding:0;margin:0; } html,body {positi...

计算机网络考研辨析(后续整理入笔记)
文章目录 体系结构物理层速率辨析交换方式辨析编码调制辨析 链路层链路层功能介质访问控制(MAC)信道划分控制之——CDMA随机访问控制轮询访问控制 扩展以太网交换机 网络层网络层功能IPv4协议IP地址IP数据报分析ICMP 网络拓扑与转发分析(重点…...
JMESPath语言
JMESPath(JSON Matching Expression Path) 一种查询语言。 主要用于从JSON文档中检索和过滤数据。 通过写表达式提取和处理JSON数据,而无需编写复杂的代码。 功能:数据提取、过滤、转换、排序。 场景:处理API响应…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
