《哥德尔证明》阅读笔记——初等命题逻辑的一致性证明过程
前言
前两节主要阐述了公理系统的发展历史,一致性问题的提出,以及希尔伯特的洞见,本节将给出哥德尔证明所需的最后一次具体背景阐述,包含两个问题:一是罗素所著的《数学原理》是为何而写?二是从数学原理中截取一段,示范对初等命题逻辑系统给出希尔伯特所设想的那种一致性的绝对证明。
《数学原理》的背景
就我们日常所接触的数学证明而言,几乎任何一个证明中都包含大量默认的推理规则和逻辑定理。
比如证明素数有无穷多个,其过程简述如下:
假定素数有有穷个,将最大的素数命名为 p p p。
那么考虑一个自然数 y = ( 2 × 3 × 5 × 7 × ⋯ × p ) y=(2\times3\times5\times7\times \cdots\times p) y=(2×3×5×7×⋯×p)。
如果 y y y是素数,那么 p p p就不是最大的素数;
如果 y y y是合数,那么它必定有素因子,且素因子不属于 { 2 , 3 , 5 , 7 , ⋯ , p } \{2,3,5,7,\cdots ,p\} {2,3,5,7,⋯,p}中任何一个,同样 p p p仍不是最大的素数。
y y y要么是素数要么是合数。
所以 p p p不是最大的素数,不存在最大的素数。
以上推论可以说足够严谨了,但较真的话能观察到其中包含了一些默认的规则,比如为什么 y y y要么是素数要么是合数?这其实是必然原理,即 p ∨ ∼ p p\lor \sim p p∨∼p,一个陈述或其非是必然的。我们日常使用这些逻辑原理而不自知,事实上,我们这种传统的逻辑演绎是严重不完整的。
逻辑的研究在近代复苏始于布尔的《逻辑的数学分析》,他发明了布尔代数为传统逻辑原理提供了精准记法,扩展了逻辑原理的研究。之后,数学家尝试将纯数学变成形式逻辑的一部分,这一思路的集大成这就是罗素的《数学原理》,这一工作的目的是将所有数论和分析的概念用纯逻辑真理的基本命题演绎出来。虽然这个过程很复杂,三卷数学原理中花费了几百页才从逻辑真理证明出1+1=2,几乎没有人想用这样的系统做数论研究,但《数学原理》实质上将数论系统的一致性化为形式逻辑本身一致性的问题,就意义上,数论的公理都是形式逻辑的定理,它的另一个意义,是把纯数学中所有陈述用一种标准方式进行编码,明确了数学证明中推论规则。
初等命题逻辑一致性的绝对证明
初等命题逻辑系统形式化
形式化的一般步骤
首先我们要明晰一般系统是如何形式化的,这里以几条原则说明。
- 指号目录:此系统需要建立一个指号目录,只允许用此目录中的指号构成串。可以理解为英文中的词汇表。
- 形成规则:表示指号形成串的规则,这个按规则形成的串,可以称为公式,或者良构串,或者叫句子。后面可能混用这些名词。形成规则只是指串是否合法,和真假无关。
- 转换规则:实际上就是推论规则,描述了公式的精细结构,从某些公式推导其他具有既定结构公式的方法。
- 初始公式:即选择一些公式作为公理。
一般记号
这里额外补充一些书中的记法,虽然下面列出了这些符号在命题逻辑系统中的含义,但应当理解的是,在完全形式化的系统中,这些意义是抽离的,本文中所有证明不需要默认这些符号有这些含义,而是把这些符号当成完全无意义的指号:
- ∼ \sim ∼是非的缩写
- ∨ \lor ∨是或的缩写
- ⊃ \supset ⊃是“如果…,那么…”的缩写,或者理解为推导出,或者叫做蕴涵。
- ∧ \land ∧是与的缩写
初等命题逻辑系统的形式化
- 指号目录的选择:包含变元和常项两种指号,变元即可以使用句子替换的记号,常项有句子连接词和标点符号。举例来说: ( p ∨ q ) ⊃ ( p ∨ q ) (p\lor q)\supset(p\lor q) (p∨q)⊃(p∨q)就是一个句子,其中, p p p和 q q q是变元,它们可以用另一个句子替换掉, ∨ ∧ ∼ ⊃ ( ) \lor\land\sim\supset () ∨∧∼⊃()等都是句子连接词或符号。
- 形成规则:
- 句子变元单独可视为一个句子(公式、良构串)。
- 如果 S S S代表一个公式,那么 ∼ ( S ) \sim(S) ∼(S)也是一个公式。
- 如果 S 1 S_1 S1和 S 2 S_2 S2都是公式,那么 ( S 1 ) ∧ ( S 2 ) (S_1)\land(S_2) (S1)∧(S2)、 ( S 1 ) ∨ ( S 2 ) (S_1)\lor(S_2) (S1)∨(S2)、 ( S 1 ) ⊃ ( S 2 ) (S_1)\supset(S_2) (S1)⊃(S2)都是公式。
- 转换规则:有两条,分别是
- 替换规则:对于一个包含句子变元的公式,总可以将其中某个变元的每一次出现都替换为一个公式,从而得到一个新的公式。比如 p ⊃ p p\supset p p⊃p可以将 p p p替换为 p ∨ q p\lor q p∨q,从而得到 ( p ∨ q ) ⊃ ( p ∨ q ) (p\lor q)\supset (p\lor q) (p∨q)⊃(p∨q)。
- 分离规则:如果有形式上是 S 1 S_1 S1和 S 1 ⊃ S 2 S_1\supset S_2 S1⊃S2的两个公式,总可以推出公式 S 2 S_2 S2。例如有 p ∨ ∼ p p\lor\sim p p∨∼p和 ( p ∨ ∼ p ) ⊃ ( p ⊃ p ) (p\lor \sim p)\supset (p\supset p) (p∨∼p)⊃(p⊃p),那么有 p ⊃ p 。 p\supset p。 p⊃p。
- 初始公式(公理选择):这个演算的公理如下:
- ( p ∨ p ) ⊃ p (p\lor p)\supset p (p∨p)⊃p
- p ⊃ ( p ∨ q ) p\supset (p\lor q) p⊃(p∨q)
- ( p ∨ q ) ⊃ ( q ∨ p ) (p\lor q)\supset (q\lor p) (p∨q)⊃(q∨p)
- ( p ⊃ q ) ⊃ ( ( r ∨ p ) ⊃ ( r ∨ q ) ) (p\supset q)\supset ((r\lor p)\supset (r\lor q)) (p⊃q)⊃((r∨p)⊃(r∨q))
系统一致性的绝对证明
以下将分步骤给出此命题逻辑系统中,一致性的绝对证明,证明步骤中在《哥德尔证明》书中没有给出的部分,大部分来自于罗素的《数学原理》。
Step1:首先,此系统中可推导出一个定理: p ⊃ ( ∼ p ⊃ q ) p\supset (\sim p\supset q) p⊃(∼p⊃q),证明过程如下。
必须先声明,《哥德尔证明》这本书有漏掉的地方,在罗素原版的《数学原理》明确给出了: p ⊃ q = def ∼ p ∨ q p\supset q\overset{\text{def}}{=}\sim p\lor q p⊃q=def∼p∨q,此处证明需要用到这个定义。
- 根据公理2, p ⊃ ( p ∨ q ) p\supset (p\lor q) p⊃(p∨q),根据替换规则,用 ∼ p \sim p ∼p取代 p p p可得: ∼ p ⊃ ( ∼ p ∨ q ) \sim p\supset(\sim p\lor q) ∼p⊃(∼p∨q)
根据定义,上式子可重写为: ∼ p ⊃ ( p ⊃ q ) \sim p\supset(p\supset q) ∼p⊃(p⊃q)
再次运用替换规则,用 ∼ p \sim p ∼p取代 p p p可得: ∼ ∼ p ⊃ ( ∼ p ⊃ q ) \sim\sim p\supset(\sim p\supset q) ∼∼p⊃(∼p⊃q)
到这一步,证明还要继续,因为这个形式系统中,抽离了现实意义,不能有“把 ∼ \sim ∼看做否定,双重否定抵消”的想法。- 第二步需要证明一个重要的性质,传递律。即若 a ⊃ b a\supset b a⊃b,且 b ⊃ c b\supset c b⊃c,则 a ⊃ c a\supset c a⊃c。由公理4出发, ( p ⊃ q ) ⊃ ( ( r ∨ p ) ⊃ ( r ∨ q ) ) (p\supset q)\supset ((r\lor p) \supset(r\lor q)) (p⊃q)⊃((r∨p)⊃(r∨q)),将 p p p取代为 b b b,将 q q q取代为 c c c,则由分离规则,通过 b ⊃ c b\supset c b⊃c和 ( b ⊃ c ) ⊃ ( ( r ∨ b ) ⊃ ( r ∨ c ) ) (b\supset c)\supset((r\lor b)\supset(r\lor c)) (b⊃c)⊃((r∨b)⊃(r∨c))立刻得出: ( r ∨ b ) ⊃ ( r ∨ c ) (r\lor b)\supset(r\lor c) (r∨b)⊃(r∨c),将 r r r用 a a a取代,得到 ( a ∨ b ) ⊃ ( a ∨ c ) (a\lor b)\supset (a\lor c) (a∨b)⊃(a∨c),再将 a a a用 ∼ a \sim a ∼a取代,得到 ( ∼ a ∨ b ) ⊃ ( ∼ a ∨ c ) (\sim a\lor b)\supset (\sim a\lor c) (∼a∨b)⊃(∼a∨c),即 ( a ⊃ b ) ⊃ ( a ⊃ c ) (a\supset b)\supset (a\supset c) (a⊃b)⊃(a⊃c),再用一次分离规则就可以得出 a ⊃ c a\supset c a⊃c,故传递律得证。
- 第三步需要证明 p ⊃ p p\supset p p⊃p。通过公理2和公理1, p ⊃ ( p ∨ p ) p\supset(p\lor p) p⊃(p∨p)和 ( p ∨ p ) ⊃ p (p\lor p)\supset p (p∨p)⊃p,再根据传递律,即可证明 p ⊃ p p\supset p p⊃p。
- 接下来需要证明, p ⊃ ∼ ∼ p p\supset\sim\sim p p⊃∼∼p。对公理3运用两次替换规则,可得 ( ∼ p ∨ ∼ q ) ⊃ ( ∼ q ∨ ∼ p ) (\sim p\lor\sim q)\supset(\sim q\lor\sim p) (∼p∨∼q)⊃(∼q∨∼p),再根据定义,可将其重写为: ( p ⊃ ∼ q ) ⊃ ( q ⊃ ∼ p ) (p\supset\sim q)\supset(q\supset\sim p) (p⊃∼q)⊃(q⊃∼p),此时再进行两次取代,将 p p p取代为 ∼ p \sim p ∼p,将 q q q取代为 p p p,可得: ( ∼ p ⊃ ∼ p ) ⊃ ( p ⊃ ∼ ( ∼ p ) ) (\sim p\supset\sim p)\supset(p\supset\sim(\sim p)) (∼p⊃∼p)⊃(p⊃∼(∼p)),对步骤3得出的 p ⊃ p p\supset p p⊃p用替换规则,得到 ∼ p ⊃ ∼ p \sim p\supset \sim p ∼p⊃∼p,再用分离规则,可得 p ⊃ ∼ ( ∼ p ) p\supset\sim(\sim p) p⊃∼(∼p)。
- 综合1中的结果和4中的结果: p ⊃ ∼ ( ∼ p ) p\supset\sim(\sim p) p⊃∼(∼p)和 ∼ ∼ p ⊃ ( ∼ p ⊃ q ) \sim\sim p\supset(\sim p\supset q) ∼∼p⊃(∼p⊃q),运用传递律可得: p ⊃ ( ∼ p ⊃ q ) p\supset(\sim p\supset q) p⊃(∼p⊃q)
Step2:在此定理的前提下,如果 S S S即其形式否定 ∼ S \sim S ∼S都可以从此命题系统中推导出来,用替换规则让 S S S代替 p p p,可得: S ⊃ ( ∼ S ⊃ q ) S\supset (\sim S\supset q) S⊃(∼S⊃q),运用分离规则,可得: ∼ S ⊃ q \sim S\supset q ∼S⊃q,再用一次分离规则,即可得到 q q q。
由于 q q q可以通过替换规则带入任何公式,那么任何公式都能通过这组公理推导出来(实际上是不可能的)。这个结论的内涵是:如果 S S S和 ∼ S \sim S ∼S都可以由这组公理推导出来,那么任何公式都可以推导出来(也就是我们常说的,假命题可以推出任何命题)。
当然为了严谨性,不能轻易否定,证明还要继续下去,这个公理系统允许推导出任何公式吗?如果找到一个公式,是确信无法由公理系统推导的,那么我们最初的前提: S S S和 ∼ S \sim S ∼S都可由这组公理推导出来就是错误的,那么系统就是一致的。
Step3:现在的任务是证明存在一个公式无法由公理推导出来,即某个公式不是定理。完成这个任务的方式是进行元数学方面的推理。基本思路是这样的:
- 找到公理的一致属性。
- 确认转换规则将遗传这个属性,所以任何公理推导出的定理都具备此属性。
- 写出一个不具备此属性的公式,那么此公式就不是定理。
重言属性
罗素这套公理系统中可以选择“重言属性”,在非形式化的常见的命题逻辑解释下,重言属性即排除没有逻辑可能性的属性,在任意可能的世界为真,比如非 p p p或 p p p。当然这种解释有悖我们形式化的初衷,还是用现实中的模型,用真假来解释。那么更抽象的重言属性的描述在此展开。
我们创建两个类 K 1 K_1 K1和 K 2 K_2 K2,同时我们将所有公式分类,分为基本公式和非基本公式,基本公式就是用作句子变元的字母,非基本公式就是排除了基本公式外的其他。
首先我们将基本公式任意放在两个类中。
非基本公式按以下规则放入两个类中:
- 如果 S 1 S_1 S1和 S 2 S_2 S2都在 K 2 K_2 K2中,那么具有 S 1 ∨ S 2 S_1\lor S_2 S1∨S2的公式也放在 K 2 K_2 K2中,否则放在 K 1 K_1 K1中。
- 如果 S 1 S_1 S1在 K 1 K_1 K1中, S 2 S_2 S2在 K 2 K_2 K2中,那么形式为 S 1 ⊃ S 2 S_1\supset S_2 S1⊃S2的公式放在 K 2 K_2 K2中,否则它放在 K 1 K_1 K1中。
- 如果 S 1 S_1 S1和 S 2 S_2 S2都在 K 1 K_1 K1中,形式为 S 1 ∧ S 2 S_1\land S_2 S1∧S2的公式被置于 K 1 K_1 K1中,否则放在 K 2 K_2 K2中。
- 如果 S S S在 K 1 K_1 K1中,那么具有 ∼ S \sim S ∼S形式的公式放于 K 2 K_2 K2中,否则置于 K 1 K_1 K1中。
此时,可以定义重言式为一个当且仅当它属于 K 1 K_1 K1类的公式。
可以考察四条公理:
-
( p ∨ p ) ⊃ p (p\lor p)\supset p (p∨p)⊃p,如果基本公式(句子变元 p p p)被分到 K 1 K_1 K1,那么根据规则1, ( p ∨ p ) (p\lor p) (p∨p)也属于 K 1 K_1 K1,根据规则2, ( p ∨ p ) ⊃ p (p\lor p)\supset p (p∨p)⊃p仍应放到 K 1 K_1 K1中;如果基本公式(句子变元 p p p)被分到了 K 2 K_2 K2,那么根据规则1, ( p ∨ p ) (p\lor p) (p∨p)属于 K 2 K_2 K2,根据规则2, ( p ∨ p ) ⊃ p (p\lor p)\supset p (p∨p)⊃p仍应放到 K 1 K_1 K1中。
-
这里以表格的形式列出第二公理的分析。
-
p p p q q q ( p ∨ q ) (p\lor q) (p∨q) p ⊃ ( p ∨ q ) p\supset(p\lor q) p⊃(p∨q) K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 2 K_2 K2 K 2 K_2 K2 K 1 K_1 K1
-
-
第三公理的分析如下。
-
p p p q q q ( p ∨ q ) (p\lor q) (p∨q) ( q ∨ p ) (q\lor p) (q∨p) ( p ∨ q ) ⊃ ( q ∨ p ) (p\lor q)\supset(q\lor p) (p∨q)⊃(q∨p) K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 2 K_2 K2 K 2 K_2 K2 K 2 K_2 K2 K 1 K_1 K1
-
-
第四公理分析如下。
-
p p p q q q r r r ( p ⊃ q ) (p\supset q) (p⊃q) ( r ∨ p ) (r\lor p) (r∨p) ( r ∨ q ) (r\lor q) (r∨q) ( r ∨ p ) ⊃ ( r ∨ q ) (r\lor p)\supset (r\lor q) (r∨p)⊃(r∨q) ( p ⊃ q ) ⊃ ( ( r ∨ p ) ⊃ ( r ∨ q ) ) (p\supset q)\supset ((r\lor p)\supset (r\lor q)) (p⊃q)⊃((r∨p)⊃(r∨q)) K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 2 K_2 K2 K 2 K_2 K2 K 1 K_1 K1 K 2 K_2 K2 K 2 K_2 K2 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 2 K_2 K2 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 2 K_2 K2 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 1 K_1 K1 K 2 K_2 K2 K 2 K_2 K2 K 2 K_2 K2 K 1 K_1 K1 K 2 K_2 K2 K 2 K_2 K2 K 1 K_1 K1 K 1 K_1 K1
-
由此可见,四条公理都具有重言属性。接下来还需要考察重言属性在转换规则下会传递。
-
对于替换规则:其实替换规则不改变重言属性已经隐含在 K K K的定义里了,基本公式即用作句子变元的字母,也是替换规则允许替换的项,而 K K K的分类中,基本公式允许任意分布在 K 1 K_1 K1或 K 2 K_2 K2中,不改变公式的重言属性。
-
对于分离规则: S 1 S_1 S1和 S 1 ⊃ S 2 S_1\supset S_2 S1⊃S2如果都具有重言属性,必须证明 S 2 S_2 S2具有重言属性,假定 S 2 S_2 S2不具有重言属性,即 S 2 S_2 S2属于 K 2 K_2 K2,这立即引起了矛盾,因为 S 1 S_1 S1位于 K 1 K_1 K1,意味着根据重言属性规则2, S 1 ⊃ S 2 S_1\supset S_2 S1⊃S2也属于 K 2 K_2 K2,前面以及假定了 S 1 ⊃ S 2 S_1\supset S_2 S1⊃S2具有重言属性,它位于 K 1 K_1 K1。
Step 4:现在可以总结前面几个步骤,给出整个证明脉络了,首先我们推出了,如果此系统允许 S S S和 ∼ S \sim S ∼S都作为定理,那么我们可以推出的所有公式都是定理,然后我们又推出系统所有的定理都是重言式,现在只要找出一个公式不是重言式,那么我们的前提就不成立。这样的公式大量存在,比如 p ∨ q p\lor q p∨q就可以不是重言式,那两个基础句子变元都可以放在 K 2 K_2 K2类中。至此,我们完成了初等命题逻辑系统一致性的绝对证明。
相关文章:

《哥德尔证明》阅读笔记——初等命题逻辑的一致性证明过程
前言 前两节主要阐述了公理系统的发展历史,一致性问题的提出,以及希尔伯特的洞见,本节将给出哥德尔证明所需的最后一次具体背景阐述,包含两个问题:一是罗素所著的《数学原理》是为何而写?二是从数学原理中…...

迪文屏开发保姆级教程—弹出键盘录入ASCII字符
本篇文章主要介绍了在DGBUS平台上使用文本录入键盘录入ASCII字符,数字和字母的教程。 文本录入键盘支持录入ASCII字符,数字和字母。 官方开发指南PDF:(不方便下载的私聊我发给你) https://download.csdn.net/download…...
)
Java,处理字符串的案例()
场景 为了得到一个都是英雄名字的字符数组,需要对如下字符串进行处理 疾风剑豪,影流之主,封魔剑魂,暗裔剑魔,无极剑圣,无双剑姬,武器大师,德邦总管,蛮族之王࿰…...

微信小程序更新机制
1/同步更新 1、定期检查更新时; 2、长期未使用,首次进入会同步更新,但在弱网或者下载新版本失败的情况下,还会使用旧版本。 2/异步更新: 启动时异步更新 3/开发者手动触发更新 在启动时异步更新的情况下,…...
CentOS 7 部署 Nacos-2.3.0 (单机版)
CentOS 7 部署 Nacos-2.3.0 (单机版) 1. 下载 Nacos 安装包 历史版本:https://github.com/alibaba/nacos/releases/ 我选的是 2.3.0 版本,https://github.com/alibaba/nacos/releases/download/2.3.0/nacos-server-2.3.0.tar.g…...
Springboot优雅实现对接口返回统一封装
前端在调用后端接口时往往不同的接口返回的数据是不一样的,但是通常我们会与前端约定一个固定的返回格式,通过固定的格式告诉他们什么时候接口是返回成功,什么时候返回失败,返回成功后他们如何拿到接口返回的数据去渲染前端页面。…...
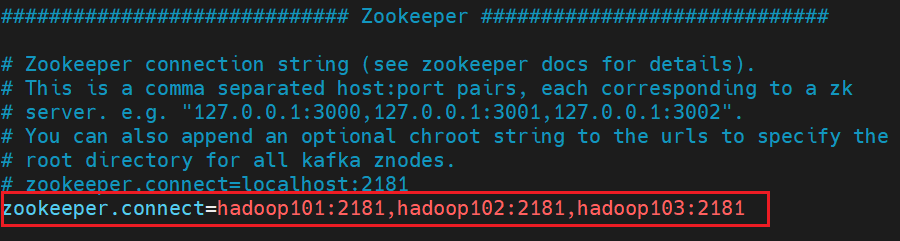
Kafka 安装与部署
目录 Kafka 下载 (1)将 kafka_2.11-2.4.1.tgz 上传至 /opt/software/ (2)解压安装包至 /opt/module/ [huweihadoop101 ~]$ cd /opt/software/ [huweihadoop101 software]$ tar -zxvf kafka_2.11-2.4.1.tgz -C ../module/&#…...

计算 N*4*4 位姿形状的逆变换,在N*3*4位姿后补充 [0,0,0,1]
针对 [N,4,4] shape 的 poses,函数 ComputeInversePoses 返回 相同 shape,但是每个 pose 都是前面的 逆 pose。 针对 [N,3,4] shape 的 poses,函数 AddIdentityToPoses 返回 在每个 [3,4] pose下加上 [0,0,0,1] 后的pose,返回的…...
人工智能可以战胜人类智慧大脑么?
引言 在当今快速发展的科技时代,人工智能的进步日新月异,引发了一场深刻的讨论:能否有一天,人工智能能够超越甚至战胜人类智慧?这个问题涉及到人类认知的广泛领域,牵涉到人类思维的深层次特质以及AI技术在…...

【数据结构和算法】 K 和数对的最大数目
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、题目描述 二、题解 2.1 方法一:双指针排序 三、代码 3.1 方法一:双指针排序 3.2 方法二࿱…...
基于ssm高校推免报名系统源码和论文
网络的广泛应用给生活带来了十分的便利。所以把高校推免报名管理与现在网络相结合,利用java技术建设高校推免报名管理系统,实现高校推免报名的信息化。则对于进一步提高高校推免报名管理发展,丰富高校推免报名管理经验能起到不少的促进作用。…...
算法设计与分析2023秋-头歌实验-实验七 动态规划
文章目录 第1关:数塔问题任务描述相关知识编程要求解题思路测试说明参考答案 第2关:最长公共子序列任务描述相关知识编程要求解题思路:测试说明参考答案 第3关:求序列-2 11 -4 13 -5 -2的最大子段和任务描述相关知识编程要求解题思…...

复杂 SQL 实现分组分情况分页查询
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、根据 camp_status 字段分为 6 种情况 1.1 SQL语句 1.2 SQL解释 二、分页 SQL 实现 2.1 SQL语句 2.2 根据 camp_type 区分返…...

JavaScript---如何完美的判断返回对象是否有值
如何判断一个对象为空是我们在开发中经常会遇到的问题,今天我们来聊聊几种经常使用的方法,以及在不同的场景下我们如何去使用。 1. JSON.stringify JSON.stringify 方法可以使对象序列化,转为相应的 JSON 格式。 js 复制代码 const obj {…...
kafka offset sasl加密连接
kafka-tool(offset) 进行SCRAM连接,直接上图 填写jaas的认证(账密 引用包)...
Android studio矩形背景颜色以及弧度的设置
在这里插入图片描述 Android的shape中主要设置的属性 corners:用于设置形状的圆角,可以设置圆角的半径、颜色等属性。 stroke:用于设置形状的边框,可以设置边框的宽度、颜色等属性。 padding:用于设置形状的内边距&…...
Acrel-1000DP分布式光伏系统在某重工企业18MW分布式光伏中应用——安科瑞 顾烊宇
摘 要:分布式光伏发电特指在用户场地附近建设,运行方式以用户侧自发自用、余电上网,且在配电系统平衡调节为特征的光伏发电设施,是一种新型的、具有广阔发展前景的发电和能源综合利用方式,它倡导就近发电,就…...
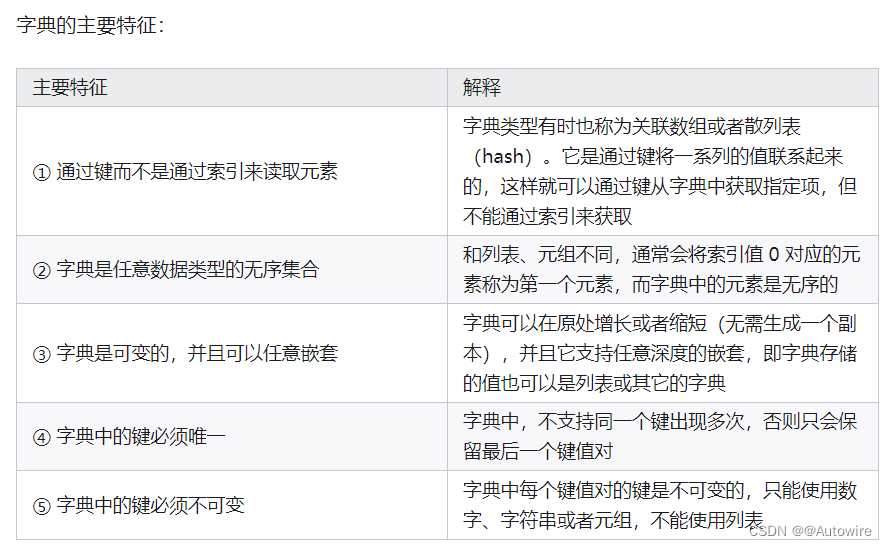
3 python基本语法 - Dict 字典
Python 中字典(dict)是一种无序的、可变的序列,它的元素以“键值对(key-value)”的形式存储。相对地,列表(list)和元组(tuple)都是有序的序列,它们…...

Magnific AI:彻底改变 AI 生成图像的升级
在我最近与 Magnific AI 的讨论中,我不仅感到惊讶,而且对该工具提供的质量和可能性着迷。我发现 Magnific AI 能够转换人工智能生成的图像(这些图像通常只能以低分辨率提供),尤其令人印象深刻,不仅在可打印…...

BKP 备份寄存器 RTC 实时时钟-stm32入门
这一章节我们要讲的主要内容是 RTC 实时时钟,对应手册,是第 16 章的位置。 实时时钟这个东西,本质上是一个定时器,但是这个定时器,是专门用来产生年月日时分秒,这种日期和时间信息的。所以学会了 STM32 的…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
