【微服务】服务间调用
当我们的应用从一个大单体拆分成多个微服务之后,服务间调用有多少种方式?服务间调用如果出现超时,如果避免雪崩,即如何做限流熔断机制,原理是什么?
服务间调用方式
OpenFeign
使用Feign进行服务间调用,我们会在启动类加@EnableFeignClients启用。
package org.springframework.cloud.openfeign;import java.lang.annotation.Documented;
import java.lang.annotation.ElementType;
import java.lang.annotation.Retention;
import java.lang.annotation.RetentionPolicy;
import java.lang.annotation.Target;
import org.springframework.context.annotation.Import;@Retention(RetentionPolicy.RUNTIME)
@Target({ElementType.TYPE})
@Documented
@Import({FeignClientsRegistrar.class})
public @interface EnableFeignClients {String[] value() default {};String[] basePackages() default {};Class<?>[] basePackageClasses相关文章:

【微服务】服务间调用
当我们的应用从一个大单体拆分成多个微服务之后,服务间调用有多少种方式?服务间调用如果出现超时,如果避免雪崩,即如何做限流熔断机制,原理是什么? 服务间调用方式 OpenFeign 使用Feign进行服务间调用,我们会在启动类加@EnableFeignClients启用。 package org.sprin…...

一句话分清C/C++声明和定义
定义告诉编译器在在哪个位置存储变量,声明没有 声明:告诉编译器,变量类型和名字 定义:告诉编译器变量存储的位置。 举例子 int i; // 这是声明定义。声明:告诉编译器变量类型int,变量名字i, // 定义&…...

《哥德尔证明》阅读笔记——初等命题逻辑的一致性证明过程
前言 前两节主要阐述了公理系统的发展历史,一致性问题的提出,以及希尔伯特的洞见,本节将给出哥德尔证明所需的最后一次具体背景阐述,包含两个问题:一是罗素所著的《数学原理》是为何而写?二是从数学原理中…...

迪文屏开发保姆级教程—弹出键盘录入ASCII字符
本篇文章主要介绍了在DGBUS平台上使用文本录入键盘录入ASCII字符,数字和字母的教程。 文本录入键盘支持录入ASCII字符,数字和字母。 官方开发指南PDF:(不方便下载的私聊我发给你) https://download.csdn.net/download…...
)
Java,处理字符串的案例()
场景 为了得到一个都是英雄名字的字符数组,需要对如下字符串进行处理 疾风剑豪,影流之主,封魔剑魂,暗裔剑魔,无极剑圣,无双剑姬,武器大师,德邦总管,蛮族之王࿰…...

微信小程序更新机制
1/同步更新 1、定期检查更新时; 2、长期未使用,首次进入会同步更新,但在弱网或者下载新版本失败的情况下,还会使用旧版本。 2/异步更新: 启动时异步更新 3/开发者手动触发更新 在启动时异步更新的情况下,…...
CentOS 7 部署 Nacos-2.3.0 (单机版)
CentOS 7 部署 Nacos-2.3.0 (单机版) 1. 下载 Nacos 安装包 历史版本:https://github.com/alibaba/nacos/releases/ 我选的是 2.3.0 版本,https://github.com/alibaba/nacos/releases/download/2.3.0/nacos-server-2.3.0.tar.g…...
Springboot优雅实现对接口返回统一封装
前端在调用后端接口时往往不同的接口返回的数据是不一样的,但是通常我们会与前端约定一个固定的返回格式,通过固定的格式告诉他们什么时候接口是返回成功,什么时候返回失败,返回成功后他们如何拿到接口返回的数据去渲染前端页面。…...
Kafka 安装与部署
目录 Kafka 下载 (1)将 kafka_2.11-2.4.1.tgz 上传至 /opt/software/ (2)解压安装包至 /opt/module/ [huweihadoop101 ~]$ cd /opt/software/ [huweihadoop101 software]$ tar -zxvf kafka_2.11-2.4.1.tgz -C ../module/&#…...

计算 N*4*4 位姿形状的逆变换,在N*3*4位姿后补充 [0,0,0,1]
针对 [N,4,4] shape 的 poses,函数 ComputeInversePoses 返回 相同 shape,但是每个 pose 都是前面的 逆 pose。 针对 [N,3,4] shape 的 poses,函数 AddIdentityToPoses 返回 在每个 [3,4] pose下加上 [0,0,0,1] 后的pose,返回的…...
人工智能可以战胜人类智慧大脑么?
引言 在当今快速发展的科技时代,人工智能的进步日新月异,引发了一场深刻的讨论:能否有一天,人工智能能够超越甚至战胜人类智慧?这个问题涉及到人类认知的广泛领域,牵涉到人类思维的深层次特质以及AI技术在…...

【数据结构和算法】 K 和数对的最大数目
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、题目描述 二、题解 2.1 方法一:双指针排序 三、代码 3.1 方法一:双指针排序 3.2 方法二࿱…...
基于ssm高校推免报名系统源码和论文
网络的广泛应用给生活带来了十分的便利。所以把高校推免报名管理与现在网络相结合,利用java技术建设高校推免报名管理系统,实现高校推免报名的信息化。则对于进一步提高高校推免报名管理发展,丰富高校推免报名管理经验能起到不少的促进作用。…...
算法设计与分析2023秋-头歌实验-实验七 动态规划
文章目录 第1关:数塔问题任务描述相关知识编程要求解题思路测试说明参考答案 第2关:最长公共子序列任务描述相关知识编程要求解题思路:测试说明参考答案 第3关:求序列-2 11 -4 13 -5 -2的最大子段和任务描述相关知识编程要求解题思…...

复杂 SQL 实现分组分情况分页查询
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、根据 camp_status 字段分为 6 种情况 1.1 SQL语句 1.2 SQL解释 二、分页 SQL 实现 2.1 SQL语句 2.2 根据 camp_type 区分返…...

JavaScript---如何完美的判断返回对象是否有值
如何判断一个对象为空是我们在开发中经常会遇到的问题,今天我们来聊聊几种经常使用的方法,以及在不同的场景下我们如何去使用。 1. JSON.stringify JSON.stringify 方法可以使对象序列化,转为相应的 JSON 格式。 js 复制代码 const obj {…...
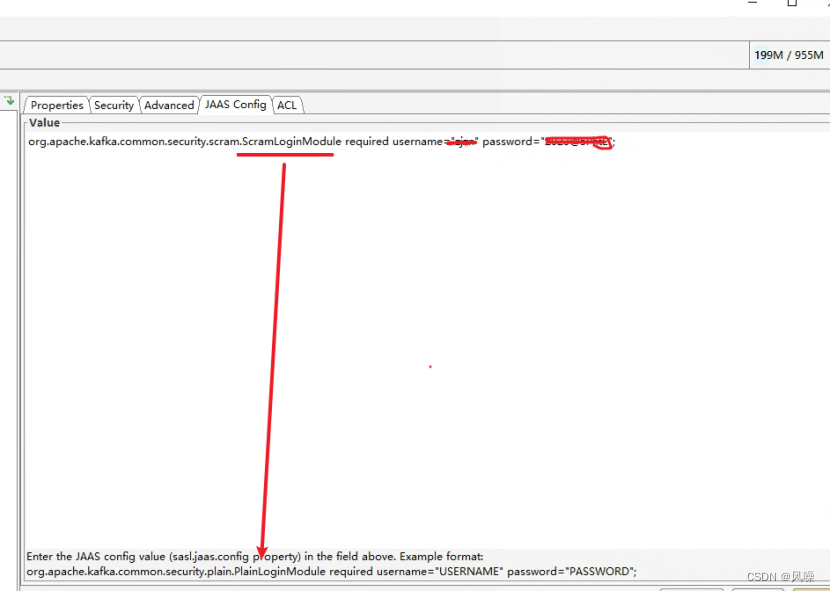
kafka offset sasl加密连接
kafka-tool(offset) 进行SCRAM连接,直接上图 填写jaas的认证(账密 引用包)...
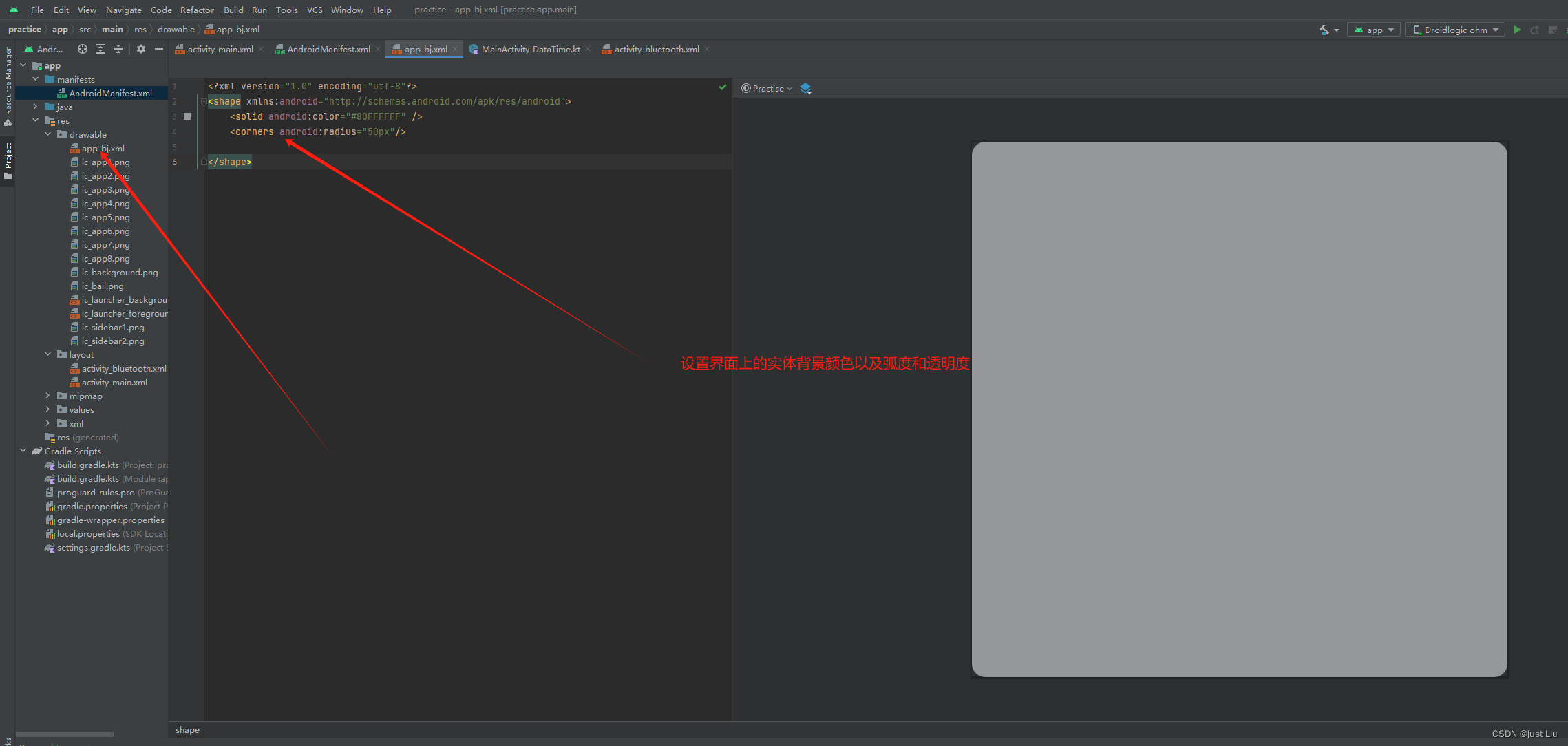
Android studio矩形背景颜色以及弧度的设置
在这里插入图片描述 Android的shape中主要设置的属性 corners:用于设置形状的圆角,可以设置圆角的半径、颜色等属性。 stroke:用于设置形状的边框,可以设置边框的宽度、颜色等属性。 padding:用于设置形状的内边距&…...
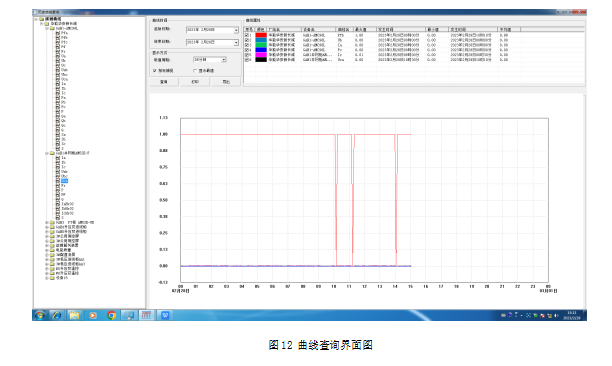
Acrel-1000DP分布式光伏系统在某重工企业18MW分布式光伏中应用——安科瑞 顾烊宇
摘 要:分布式光伏发电特指在用户场地附近建设,运行方式以用户侧自发自用、余电上网,且在配电系统平衡调节为特征的光伏发电设施,是一种新型的、具有广阔发展前景的发电和能源综合利用方式,它倡导就近发电,就…...
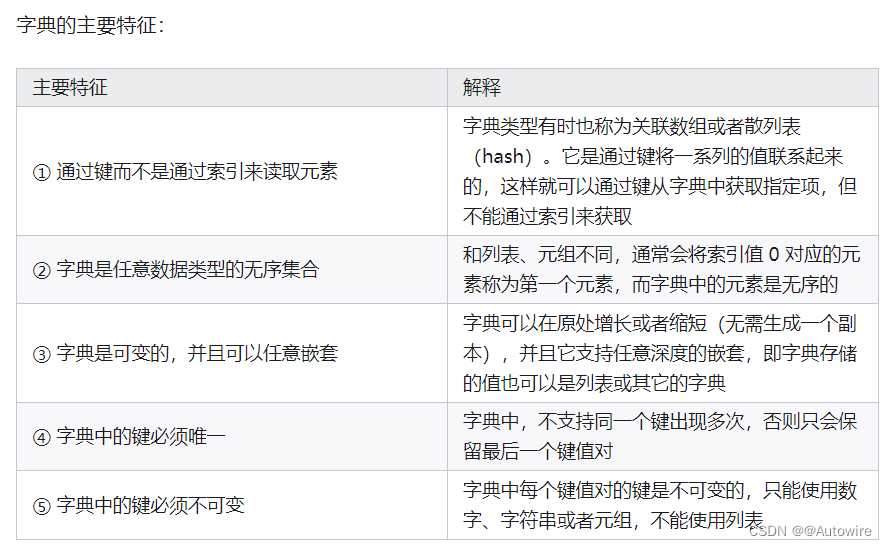
3 python基本语法 - Dict 字典
Python 中字典(dict)是一种无序的、可变的序列,它的元素以“键值对(key-value)”的形式存储。相对地,列表(list)和元组(tuple)都是有序的序列,它们…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
