C++数据结构——二叉搜索树详解
目录
一,关于二叉搜索树
1.1 概念
1.2 基本结构
二,二叉搜索树接口实现
2.1 插入
2.2 查找
2.3 打印
2.4* 删除
三,二叉搜索树接口递归实现
3.1 查找
3.2 插入
3.3 删除
四,二叉搜索树的默认成员函数
五,测试代码
六,二叉搜索树的应用
6.1 KeyValue
6.2 改造二叉搜索树
6.3 测试代码
6.3.1 查找单词
6.3.2 统计水果出现的次数
一,关于二叉搜索树
1.1 概念
二叉搜索树又称二叉排序树,具有以下性质:
①一节点左子树节点的值都小于该节点的值
②一节点右子树的值都大于该节点的值
③一节点的左右子树也是二叉搜索树
简单来说就是左孩子节点比我小,右孩子节点比我大,所以以中序遍历二叉搜索树时打印的结果是从小到大的,所以二叉搜索树又被称为二叉排序树
1.2 基本结构
template<class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public://接口以及默认成员函数实现private:Node* _root = nullptr;
}二,二叉搜索树接口实现
2.1 插入
二叉搜索树的插入不难,如果数为空直接新增根节点,如果不为空,比我小走左边,比我大走右边,走到空的时候新增节点并完成链接,如下代码和注释
bool Insert(const K& key)
{if (_root == nullptr){_root = new Node(key);return true;}//先找到合适的插入位置Node* parent = nullptr; //创建parent记录cur上一个节点位置,方便后面链接Node* cur = _root;while (cur){if (cur->_key < key) //插入的值比我大,走右边{parent = cur; //记录上一个位置cur = cur->_right;}else if (cur->_key > key) //插入的值比我小,走左边{parent = cur; //记录上一个位置cur = cur->_left;}else//插入的值相等,插入失败,搜索二叉树不允许数据相等{return false;}}//找到插入位置,创建节点开始插入cur = new Node(key);//cur是局部变量,出了函数作用域后没了,不能直接cur赋值新节点//所以需要把前后链接起来,这时候轮到我们的parent登场了if (key > parent->_key) //插入的值比父节点大,走右边{parent->_right = cur;}else //插入的值比父节点小,走左边{parent->_left = cur;}return true;
}2.2 查找
由于二叉搜索树的性质,每次查找一个树的时候只需要走树的高度次就可以查到了,查找效率非常高,所以二叉搜索树还有个名称叫做二叉查找树
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key)//查找的值比我大,走右边{cur = cur->_right;}else if (cur->_key > key)//查找的值比我小,走左边{cur = cur->_left;}else//查找成功{return true;}}return false; //查找失败
}2.3 打印
打印我们以中序遍历打印,所以我们使用递归实现打印接口,如下代码:
public:void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}
2.4* 删除
由于二叉搜索树关联式容器的特殊性质,删除一个节点会改变整个容器的结构与性质,所以每个关联式容器的删除操作需要做非常多的处理
对于二叉搜索树的删除,我们大致分为下面几个情况:
①:删除一个节点,需要让被删除节点的父节点指向被删除节点的左孩子节点
②:删除一个节点,需要让被删除节点的父节点指向被删除节点的右孩子节点
③:在被删除节点的右子树找一个最大值的节点替换两个节点的值,再进行删除(或者找左子树最大的点替换)
如下图

具体实现结合下面代码和注释:
bool Erase(const K& key)//难
{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//找到了,开始删除{// 1、左为空if (cur->_left == nullptr)//要删除的节点的左子树为空{if (cur == _root)//极端情况,要干掉的是根{_root = cur->_right;}else{if (cur == parent->_left) //cur是父亲的左{parent->_left = cur->_right;//让父亲的左指向要删除节点的右,因为cur的左为空}else //cur是父亲的右{parent->_right = cur->_right; //让父亲的右指向要删除节点的右,因为cur的左为空}}delete cur;cur = nullptr;}// 2、右为空else if (cur->_right == nullptr)//要删除的节点的右子树为空{if (_root == cur)//极端情况,要干掉的是根{_root = cur->_left;}else{if (cur == parent->_left) //cur是父亲的左{parent->_left = cur->_left; //让父亲的左指向要删除节点的左,因为cur的右为空}else //cur是父亲的右{parent->_right = cur->_left;//让父亲的右指向要删除节点的左,因为cur的右为空}}delete cur;cur = nullptr;}// 3、左右都不为空else{// 找右子树最小节点 或 找左子树的最大节点 替代要删除的值Node* pminRight = cur;Node* minRight = cur->_right;//找右树最小节点while (minRight->_left){pminRight = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;//交换要删除的值if (pminRight->_left == minRight){pminRight->_left = minRight->_right;}else //这里看不懂可以结合上面的那个图中的要删除3和8的场景来理解{pminRight->_right = minRight->_right;}delete minRight;}return true;}}//没找到,要删除的值不存在return false;
}三,二叉搜索树接口递归实现
3.1 查找
public:bool FindR(const K& key)///递归查找{return _FindR(_root, key);}private:bool _FindR(Node* root,const K& key)//递归查找子函数{//最多找高度次,O(h) h是树的高度if (root == nullptr) return false;if (root->_key < key)return _FindR(root->_right,key);else if (root->_key > key)return _FindR(root->_left, key);else return true;}3.2 插入
实现插入子递归函数的时候,我们选择用Node* &root做函数参数,原因如下:
插入的目标是插入合适的值,并且和父亲链接起来,比如要在某个节点右边插入一个值,递归时就是 _Insert(root->right,key),我们用Node* &root之后,这个root就间接代表了上一个节点的right指针,然后我们再root = new Node(key),相当于生成一个新节点并直接赋值给父节点的右,间接完成链接,如下代码
public:bool InsertR(const K& key)//递归插入{return _InsertR(_root, key);}private:bool _InsertR(Node* &root, const K& key)//递归插入{if (root == nullptr){root = new Node(key);//root是形参,所以前面用引用return true;}if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);else //相等return false;}3.3 删除
删除我们和插入同理,用Node* &root做返回值,利用我们上面的思想完成递归实现,如下代码:
public:bool EraseR(const K& key){return _EraseR(_root, key);}private:bool _EraseR(Node* &root, const K& key){if (root == nullptr)return false;if (key > root->_key)return _EraseR(root->_right, key);else if (key < root->_key)return _EraseR(root->_left, key);else//找到了,开始删除{Node* del = root;if (root->_left == nullptr){//间接完成链接,这里的root在递归中可以间接认为是上一个节点的right或left,只是用了一个root引用来代替root = root->_right; }else if(root->_right == nullptr){root = root->_left;}else{//找右子树最小(最左)节点替换删除Node* min = root->_right;while (min->_left){min = min->_left;}swap(root->_key,min->_key);return _EraseR(root->_right, key);}delete del;return true;}}
四,二叉搜索树的默认成员函数
public://由于我们自己实现了析构函数,所以编译器不会自动生成默认构造//这条语句强制编译器生成默认构造函数BSTree() = default;BSTree(const BSTree<K>& t)//拷贝构造{_root = _Copy(t._root);}~BSTree()//析构{_Destory(_root);}//t2=t1BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}private:Node* _Copy(Node* root){if (root == nullptr){return nullptr;}Node* copyRoot = new Node(root->_key);copyRoot->_left = _Copy(root->_left);copyRoot->_right = _Copy(root->_right);return copyRoot;}void _Destory(Node* &root){if (root == nullptr){return;}//先删左再删右再删根,后序_Destory(root->_left);_Destory(root->_right);delete root;root = nullptr;}五,测试代码
int main()
{BSTree<int> t1;int a[] = { 8,3,1,10,6,4,7,14,13,4,3,4 };for (auto e : a){t1.Insert(e);}BSTree<int> t2 = t1;t1.InOrder();t2.InOrder();cout << "----------------" << endl;t1.Insert(15);t1.Insert(5);t2.Erase(8);t2.Erase(13);cout << t1.Find(15) << endl;cout << t2.Find(13) << endl;cout << "----------------" << endl;t1.InOrder();t2.InOrder();return 0;
}六,二叉搜索树的应用
6.1 KeyValue
1,Key模型:只有Key作为关键码,结构中只需存储Key,搜索时只搜索Key
比如:给一个单词word,判断该单词是否拼写正确,方法如下
①以词库中所有单词集合中的每个单词作为Key构建一颗搜索二叉树
②在二叉搜索树中查找该单词的存在,存在则拼写正确,不存在则拼写错误
2,KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。
①比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word,chinese>就构成一种键值对
②再比如统计单词次数,统计成功后,给定单词就可以快速找到其出现的次数,单词与其出现次数就是<word,count>就构成一种键值对
6.2 改造二叉搜索树
template<class K, class V>
struct BSTreeNode
{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}
};
template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}//找空位置插入Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key)//插入的值比我大,走右边{parent = cur;cur = cur->_right;}else if (cur->_key > key)//插入的值比我小,走左边{parent = cur;cur = cur->_left;}else//插入的值相等,插入失败{return false;//搜索二叉树不允许数据相等}}cur = new Node(key, value);//cur是局部变量,出了函数作用域后没了,需要把前后链接起来//创建parent记录cur上一个节点位置,方便链接if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}void InOrder(){_InOrder(_root);}Node* Find(const K& key)//允许修改{Node* cur = _root;while (cur){if (cur->_key < key)//插入的值比我大,走右边{cur = cur->_right;}else if (cur->_key > key)//插入的值比我小,走左边{cur = cur->_left;}else//插入的值相等,查找成功{return cur;}}return nullptr;}
private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;;_InOrder(root->_right);}bool FindR(const K& key)///递归查找{return _FindR(_root, key);}Node* _root = nullptr;
};6.3 测试代码
6.3.1 查找单词
void TestBSTree1()
{BSTree<string, string> dict;dict.Insert("sort", "排序");dict.Insert("left", "左边");dict.Insert("right", "右边");dict.Insert("string", "字符串");dict.Insert("insert", "插入");string str;while (cin >> str){BSTreeNode<string, string>* ret = dict.Find(str);if (ret){cout << ":" << ret->_value << endl;}else{cout << "->无此单词" << endl;}}
}
6.3.2 统计水果出现的次数
void TestBSTree2()
{string arr[] = { "苹果","苹果", "苹果", "苹果", "苹果", "香蕉","草莓","苹果", };BSTree<string, int> countTree;for (auto& str : arr){//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret)//找到水果名{ret->_value++;}else//没有找到水果,该水果第一次出现{countTree.Insert(str, 1);}}countTree.InOrder();
}
相关文章:

C++数据结构——二叉搜索树详解
目录 一,关于二叉搜索树 1.1 概念 1.2 基本结构 二,二叉搜索树接口实现 2.1 插入 2.2 查找 2.3 打印 2.4* 删除 三,二叉搜索树接口递归实现 3.1 查找 3.2 插入 3.3 删除 四,二叉搜索树的默认成员函数 五,…...
ros2机器人在gazebo中移动方案
原文连接Gazebo - Docs: Moving the robot (gazebosim.org) 很重要的地方:使用虚拟机运行Ubuntu的时候,需要关闭”加速3D图形“的那个选项,否则gazebo无法正常显示。 Moving the robot(使用命令移动机器人示例) In t…...
学习Java第74天,Ajax简介
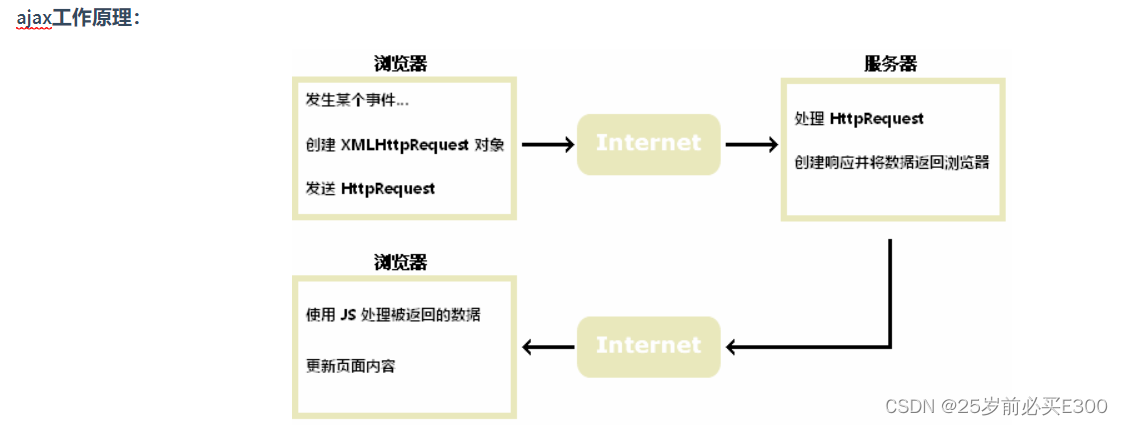
什么是ajax AJAX Asynchronous JavaScript and XML(异步的 JavaScript 和 XML)。 AJAX 不是新的编程语言,而是一种使用现有标准的新方法。 AJAX 最大的优点是在不重新加载整个页面的情况下,可以与服务器交换数据并更新部分网页…...

【Java面试题】在Java中String,Stringbuffer,StringBuilder的区别?
Hi i,m JinXiang ⭐ 前言 ⭐ 本篇文章主要介绍在Java中String,Stringbuffer,StringBuilder的区别以及部分理论知识 🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁 🍉博主收将持续更新学习记录…...

让AIGC成为你的智能外脑,助力你的工作和生活
人工智能成为智能外脑 在当前的科技浪潮中,人工智能技术正在以前所未有的速度改变着我们的生活和工作方式。其中,AIGC技术以其强大的潜力和广泛的应用前景,正在引领着这场革命。 AIGC技术是一种基于人工智能的生成式技术,它可以通…...

ubuntu12.04 源
替换 /etc/apt/sources.list deb http://old-releases.ubuntu.com/ubuntu precise main restricted universe multiverse deb http://old-releases.ubuntu.com/ubuntu precise-security main restricted universe multiverse deb http://old-releases.ubuntu.com/ubu…...

openssl数据压缩
介绍 数据压缩是将原有数据通过某种压缩算法计算得到相对数据量小的过程。这种过程是可逆的,即能通过压缩后的数据恢复出原数据。数据压缩能够节省存储空间,减轻网络负载。 在即需要加密又需要压缩的情况下,必须先压缩再加密,次…...
SQLturning:定位连续值范围起点和终点
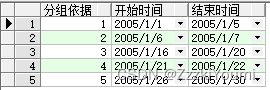
在上一篇blog说到,如何去优化查询连续值范围,没看过的朋友,上篇blog链接[在此]。(https://blog.csdn.net/weixin_42575078/article/details/135067645?spm1001.2014.3001.5501) 那么今天来说说怎么将连续的数据合并,然后返回合并…...

饥荒Mod 开发(十七):手动保存和加载,无限重生
饥荒Mod 开发(十六):五格装备栏 饥荒Mod 开发(十八):Mod 添加配置选项 饥荒游戏会自动保存,本来是一个好的机制,但是当角色死亡的时候存档会被删除,又要从头开始,有可能一不小心玩了很久的档就直接给整没了…...

Skywalking系列之最新版9.2.0-JavaAgent本地构建
MAC 10.15.7IDEA 2021.2skywalking-agent 9.2.0-SNAPSHOTJDK 17/21 (最新的代码要看最新的要求,注意不能使用JDK8,会构建失败)Maven 3.6.0 关于本地构建JavaAgent源码 1、获取源码,加载submodule 分步执行: git clone https:/…...
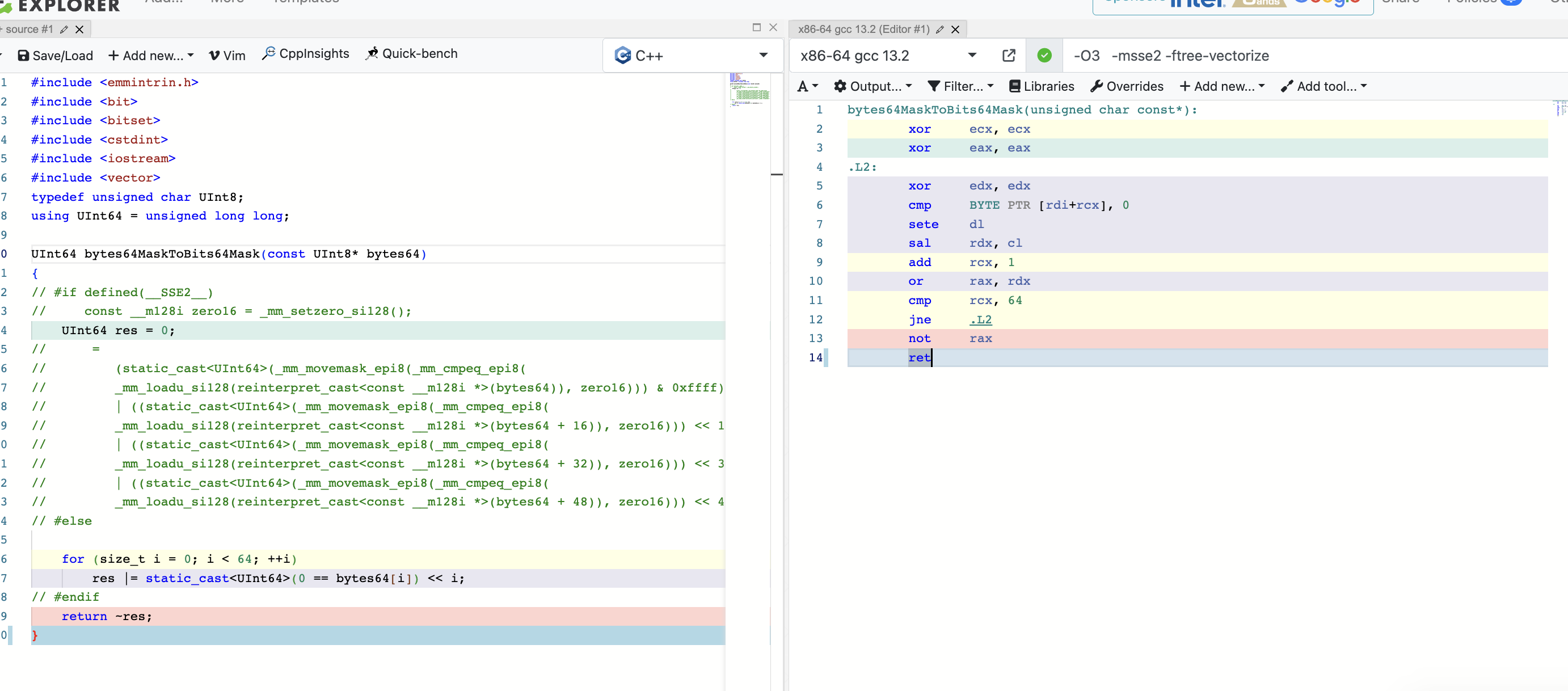
olap/clickhouse-编译器优化与向量化
本文主要结合15721和clickhouse源码来聊聊向量化,正好我最近也在用Eigen做算子加速,了解下还是有好处的。 提示编译器 提示编译器而不是复杂化简单的代码 什么时候使用汇编,什么时候使用SIMD?下面有几个基本原则: …...
RK3399平台开发系列讲解(内核入门篇)网络协议的分层
🚀返回专栏总目录 文章目录 一、应用层二、传输层三、网络层四、数据链路层(Data Link Layer)五、物理层沉淀、分享、成长,让自己和他人都能有所收获!😄 📢对于多数的应用和用户而言,使用互联网的一个基本要求就是数据可以无损地到达。用户通过应用进行网络通信...
Idea远程debugger调试
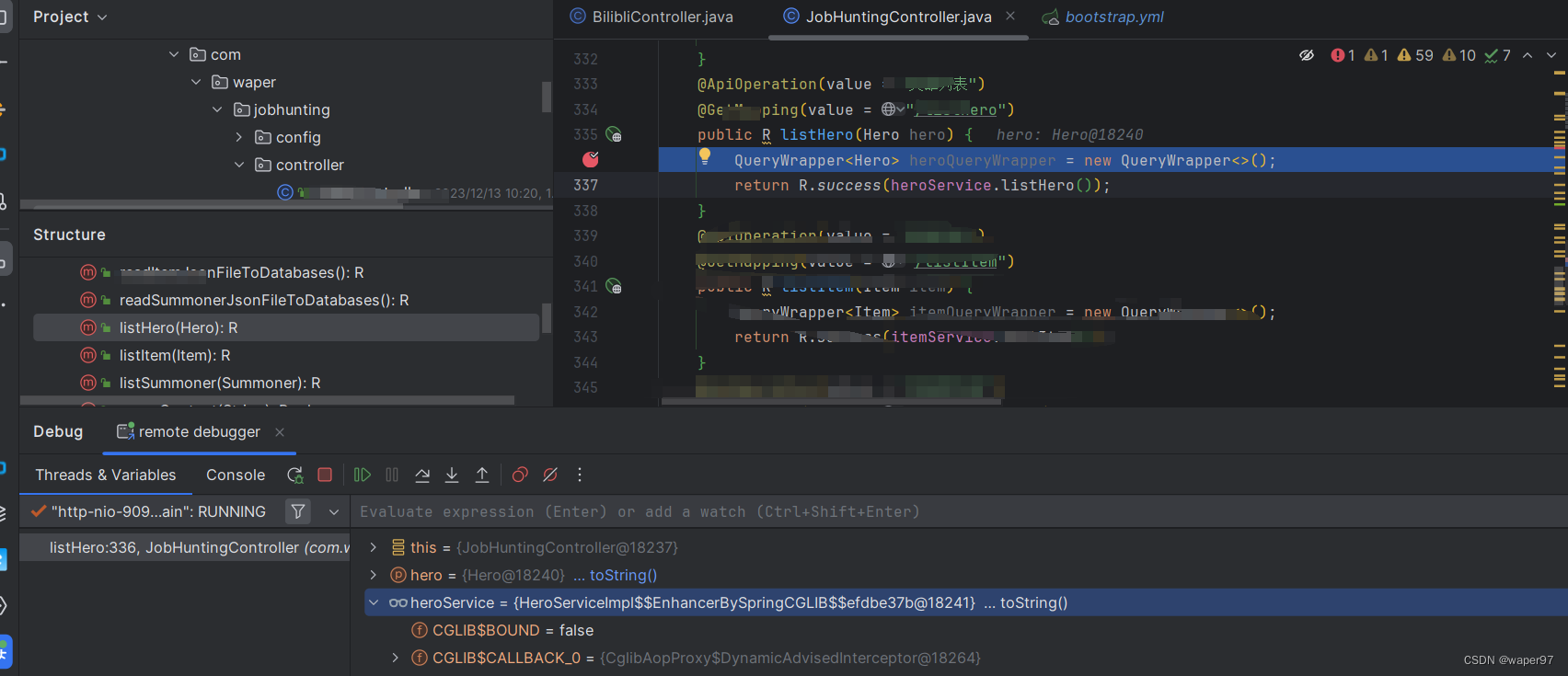
当我们服务部署在服务器上,我们想要像在本地一样debug,就可以使用idea自带的Remote JVM Debug 创建Remote JVM Debug服务器启动jar打断点进入断点 当我们服务部署在服务器上,我们想要像在本地一样debug,就可以使用idea自带的 Remote JVM Debug) 创建Rem…...
MATLAB - Gazebo 仿真环境
系列文章目录 前言 机器人系统工具箱(Robotics System Toolbox™)为使用 Gazebo 模拟器可视化的模拟环境提供了一个界面。通过 Gazebo,您可以在真实模拟的物理场景中使用机器人进行测试和实验,并获得高质量的图形。 Gazebo 可在…...
selenium自动化webdriver下载及安装
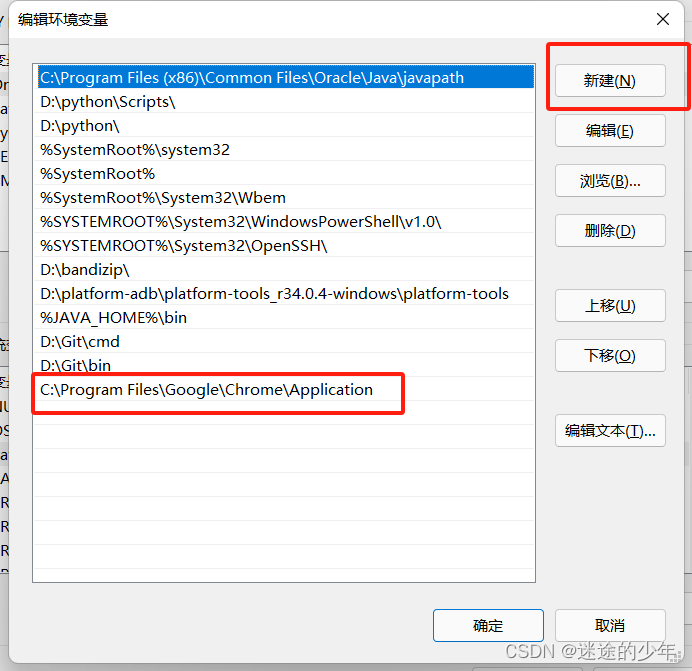
1、确认浏览器的版本 在浏览器的地址栏,输入chrome://version/,回车后即可查看到对应版本 2、找到对应的chromedriver版本 2.1 114及之前的版本可以通过点击下载chromedriver,根据版本号(只看大版本)下载对应文件 2.2 116版本通过…...
网络基础介绍
1.网线制作 1.1 网线制作需要的工具 网线 网线钳 水晶头 测试仪 编辑 1.2 网线的标准 1.3 网线的做法 2.集线器&交换机&路由器的介绍 3.OSI七层模型 4.路由器的设置 4.1 常见的路由器设置地址 4.2 常见的路由器账号密码 4.3 登录路由器 设置访客网…...

Java中四种引用类型(强、软、弱、虚)
目录 引言 强引用(Strong References) 软引用(Soft References) 弱引用(Weak References) 虚引用(Phantom References) 引用类型的应用场景 总结 引言 Java中的引用类型是管理…...
【MyBatis学习笔记】MyBatis基础学习
MyBatis基础 MyBatis简介MyBatis特性MyBatis下载和其他持久化层技术对比 核心配置文件详解默认的类型别名 搭建MyBatis开发环境创建maven工程创建MyBatis的核心配置文件创建mapper接口创建MyBatis的映射文件通过junit测试功能加入log4j日志功能 MyBatis获取参数值的两种方式&am…...
还在为论文焦虑?免费AI写作大师帮你搞定
先来看1分钟的视频,对于要写论文的你来说,绝对有所值! 还在为写论文焦虑?免费AI写作大师来帮你三步搞定 第一步:输入关键信息 第二步:生成大纲 稍等片刻后,专业大纲生成(由于举例&am…...
)
3.10【窗口】窗口使用示例(窗口缩放 三)
五,从窗口所有者放大 要从窗口的所有者本身进行放大,可以将源图像矩形设置得比窗口小。可以想象我们在一张图片中选取一部分进行放大的操作。 屏幕使用默认位置 (0,0) 作为源矩形、窗口和显示器显示的左上角。要放大源图形的特定区域,必须设置源矩形的大小。 源矩形由这些…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...
