【算法系列篇】递归、搜索和回溯(四)

文章目录
- 前言
- 什么是决策树
- 1. 全排列
- 1.1 题目要求
- 1.2 做题思路
- 1.3 代码实现
- 2. 子集
- 2.1 题目要求
- 2.2 做题思路
- 2.3 代码实现
- 3. 找出所有子集的异或总和再求和
- 3.1 题目要求
- 3.2 做题思路
- 3.3 代码实现
- 4. 全排列II
- 4.1 题目要求
- 4.2 做题思路
- 4.3 代码实现
前言
前面我们通过几个题目基本了解了解决递归类问题的基本思路和步骤,相信大家对于递归多多少少有了更加深入的了解。那么本篇文章我将为大家分享结合决策树来解决递归、搜索和回溯相关的问题。
什么是决策树
决策树是一种基本的分类与回归方法。在分类问题中,决策树通过构建一棵树形图来对数据进行分类。树的每个节点表示一个特征属性,每个分支代表一个特征属性上的判断条件,每个叶节点代表一个类别。在回归问题中,决策树可以预测一个实数值。
下面是一个简单的决策树:
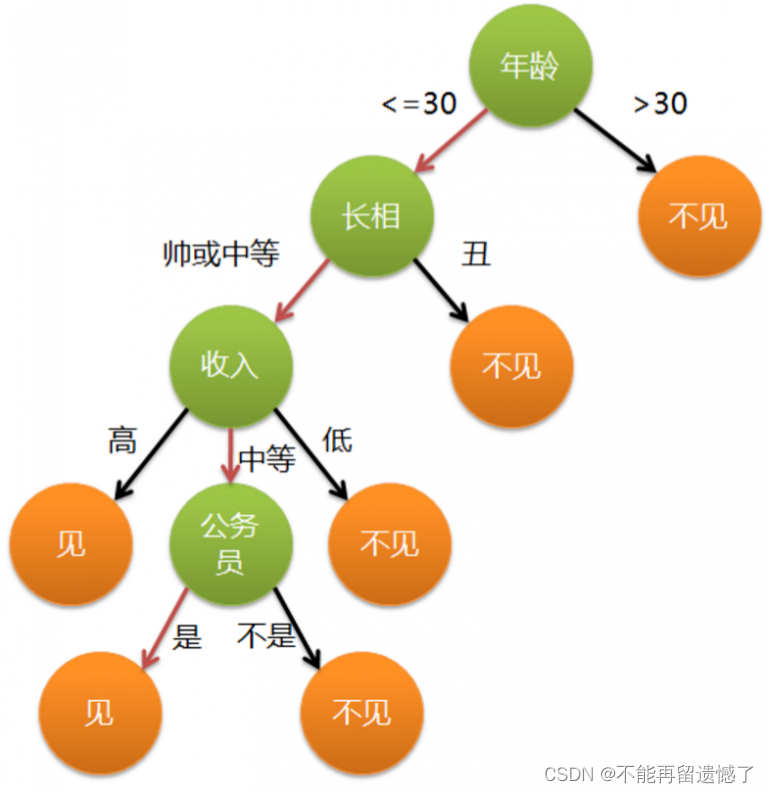
知道了什么是决策树,下面我们将运用决策树来解决实际问题。
1. 全排列
https://leetcode.cn/problems/permutations/
1.1 题目要求
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
提示:
1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同
class Solution {public List<List<Integer>> permute(int[] nums) {}
}
1.2 做题思路
相信大家肯定做过跟排列相关的问题,就是三个人坐座位的问题。第一座位可以坐A、B、C 任何一个人,如果第一个座位坐的是 A 的话,那么第二个位子 A 就不能再坐了,第二个位子就只能在 B、C 之间选择了,如果 B 选择了第二个位子,那么第三个位置就只能 C 选择了。所以这个问题通过决策树来体现的话就是这样的:
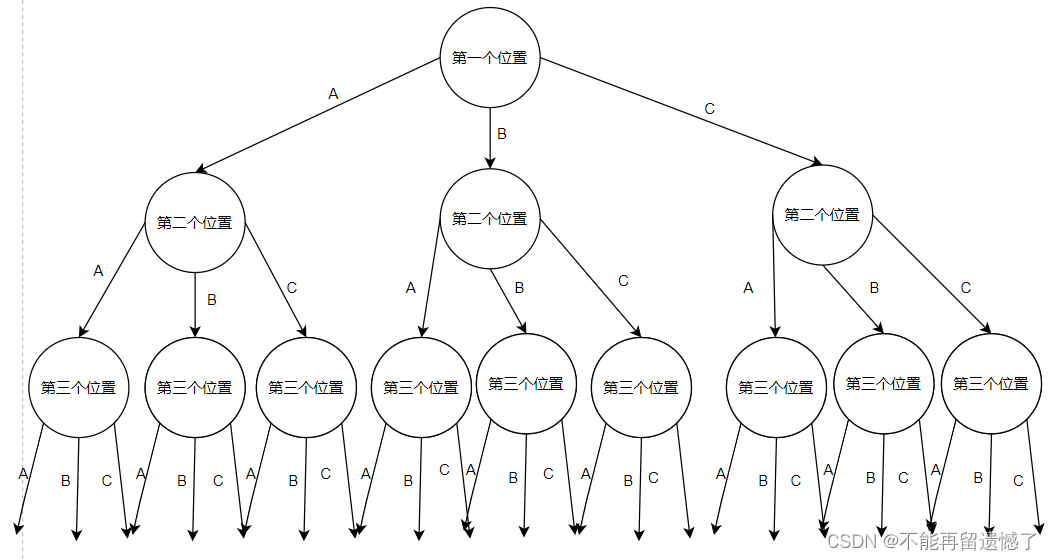
但是上面的图我们会发现这几种情况会有重复的情况,那么我们如何筛选掉这些重复的情况呢?可以使用一个标记数组来记录已经选择过的元素,当下一次选择的时候就选择这个标记数组中没有被选择的剩下的元素的其中一个。这道题目跟上面的例子的思路是一样的,这里我就不为大家再画一个图了。
那么这道题使用代码的思想该如何解决呢?每次递归我们还是将数组中的所有元素都给列举出来,不过我们需要根据标记数组中元素的使用情况来选择是否可以选择这个元素,如果某个元素没有被选择,那么这次就选择这个元素,将这个元素标记为已使用,然后继续递归,当当前情况列举完成之后就需要恢复现场,当路径集合中记录的元素的个数和数组中的元素个数相同的时候,就说明一种情况已经列举完成,就可以将当前情况添加进ret集合中,返回。
1.3 代码实现
class Solution {List<Integer> path;List<List<Integer>> ret;boolean[] vis;public List<List<Integer>> permute(int[] nums) {//对全局变量进行初始化path = new ArrayList<>();ret = new ArrayList<>();vis = new boolean[nums.length];dfs(nums);return ret;}private void dfs(int[] nums) {//当path中元素的大小等于数组的大小,就说明一种情况已经列举完成,这事需要我们将当前path中的数据添加进ret中,并且返回if (path.size() == nums.length) {ret.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {if (vis[i] == false) {path.add(nums[i]);//将当前元素标记为已使用vis[i] = true;//考虑该位置之后的其他元素的选择dfs(nums);//恢复现场path.remove(path.size() - 1);vis[i] = false;}}}
}
2. 子集
https://leetcode.cn/problems/subsets/
2.1 题目要求
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
提示:
1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同
class Solution {public List<List<Integer>> subsets(int[] nums) {}
}
2.2 做题思路
前面全排列中是当路径集合中的元素个数和数组中的元素的个数相同的时候视为一种情况,这道题目就不一样了,这个是数组的子集,也就是说每一种情况的元素的个数可能是不一样的,所以我们路径集合每新添加一个元素就可以视为一种情况,就需要将路径中的元素添加进ret集合中,思路跟上一道题目是类似的,都是通过决策树递归来实现的,但是呢?仔细看题目可以发现,就是集合[1,2],[2,1]是一种情况,也就是说子集的选择跟顺序无关,那么我们又该如何避免出现重复的情况呢?
这其实也不难,想想如果是在数学中我们会怎样思考?如果当前位置我们选择了某个元素,那么后面的位置我们就从这个元素的后面元素中去选择。

所以通过代码体现的话,就是我们可以使用一个 pos 变量来记录当前位置选择的元素的下标,然后下一个位置选择元素递归的话,我们就从 pos 的下一个位置开始选择。
2.3 代码实现
class Solution {List<Integer> path;List<List<Integer>> ret;public List<List<Integer>> subsets(int[] nums) {path = new ArrayList<>();ret = new ArrayList<>();dfs(nums, 0)return ret;}private void dfs(int[] nums, int pos) {//进入这个函数就可以将path中的结果添加进ret中,这样就可以将空集的情况给考虑上ret.add(new ArrayList<>(path));//循环的话,就从pos位置开始遍历for (int i = pos; i < nums.length; i++) {path.add(nums[i]);dfs(nums, i + 1);path.remove(path.size() - 1);}}
}
3. 找出所有子集的异或总和再求和
https://leetcode.cn/problems/sum-of-all-subset-xor-totals/
3.1 题目要求
一个数组的 异或总和 定义为数组中所有元素按位 XOR 的结果;如果数组为 空 ,则异或总和为 0 。
例如,数组 [2,5,6] 的 异或总和 为 2 XOR 5 XOR 6 = 1 。
给你一个数组 nums ,请你求出 nums 中每个 子集 的 异或总和 ,计算并返回这些值相加之 和 。
注意:在本题中,元素 相同 的不同子集应 多次 计数。
数组 a 是数组 b 的一个 子集 的前提条件是:从 b 删除几个(也可能不删除)元素能够得到 a 。
示例 1:
输入:nums = [1,3]
输出:6
解释:[1,3] 共有 4 个子集:
- 空子集的异或总和是 0 。
- [1] 的异或总和为 1 。
- [3] 的异或总和为 3 。
- [1,3] 的异或总和为 1 XOR 3 = 2 。
0 + 1 + 3 + 2 = 6
示例 2:
输入:nums = [5,1,6]
输出:28
解释:[5,1,6] 共有 8 个子集:
- 空子集的异或总和是 0 。
- [5] 的异或总和为 5 。
- [1] 的异或总和为 1 。
- [6] 的异或总和为 6 。
- [5,1] 的异或总和为 5 XOR 1 = 4 。
- [5,6] 的异或总和为 5 XOR 6 = 3 。
- [1,6] 的异或总和为 1 XOR 6 = 7 。
- [5,1,6] 的异或总和为 5 XOR 1 XOR 6 = 2 。
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28
示例 3:
输入:nums = [3,4,5,6,7,8]
输出:480
解释:每个子集的全部异或总和值之和为 480 。
提示:
1 <= nums.length <= 12
1 <= nums[i] <= 20
class Solution {public int subsetXORSum(int[] nums) {}
}
3.2 做题思路
这道题目跟上面的子集思路基本上没什么区别,之不过上面的子集是要求出所有子集的情况,而这道题目是求出所有子集异或之后的总和。因为思路基本跟上个题一样,所以我们直接来看代码。
3.3 代码实现
class Solution {int path;int ret;public int subsetXORSum(int[] nums) {dfs(nums, 0);return ret;}private void dfs(int[] nums, int pos) {//前面是将集合添加进ret中,这里我们是将每种情况加进ret中ret += path;for (int i = pos; i < nums.length; i++) {//这里我们不是将新加入的元素加入到path集合中,而是将新加入的元素和之前path元素的异或的结果异或path ^= nums[i];dfs(nums, i + 1);//恢复现场(两个相同的元素异或,结果为0)path ^= nums[i];}}
}
4. 全排列II
https://leetcode.cn/problems/permutations-ii/
4.1 题目要求
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
1 <= nums.length <= 8
-10 <= nums[i] <= 10
class Solution {public List<List<Integer>> permuteUnique(int[] nums) {}
}
4.2 做题思路
这道题目跟 全排列I 是不一样的,全排列I 中不存在重复的元素,但是这道题目中存在重复的元素,也就是说[1, 1, 2] 和 [1, 1, 2] 是同一个排列,这不看起来就是同一个排列吗?难道还能不同吗?其实这里的 1 不是同一个1,[1(下标为0), 1(下标为1), 2],[1(下标为1), 1(下标为0), 2],全排列I 中我们只需要使用一个标记数组来避免同一个元素被重复使用的情况,而这个 全排列II 中,我们还需要筛选出因元素相同而导致的相同排列的情况。那么如何筛选呢?我们来看个例子:

4.3 代码实现
class Solution {List<Integer> path;List<List<Integer>> ret;boolean[] vis;public List<List<Integer>> permuteUnique(int[] nums) {path = new ArrayList<>();ret = new ArrayList<>();vis = new boolean[nums.length];//首先将重复元素给排序到一起Arrays.sort(nums);dfs(nums);return ret;}private void dfs(int[] nums) {if (path.size() == nums.length) {ret.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {if (vis[i] == false && (i == 0 || (nums[i - 1] != nums[i]) || vis[i - 1] == true)) {path.add(nums[i]);vis[i] = true;dfs(nums);//恢复现场path.remove(path.size() - 1);vis[i] = false;}}}
}
相关文章:

【算法系列篇】递归、搜索和回溯(四)
文章目录 前言什么是决策树1. 全排列1.1 题目要求1.2 做题思路1.3 代码实现 2. 子集2.1 题目要求2.2 做题思路2.3 代码实现 3. 找出所有子集的异或总和再求和3.1 题目要求3.2 做题思路3.3 代码实现 4. 全排列II4.1 题目要求4.2 做题思路4.3 代码实现 前言 前面我们通过几个题目…...
Windows 系统下本地单机搭建 Redis(一主二从三哨兵)
目录 一、Redis环境准备: 1、下载redis 2、Windows下的.msi安装和.zip格式区别: 二、哨兵介绍: 1、一主二从三哨兵理论图: 2.哨兵的主要功能: 3.哨兵用于实现 redis 集群的高可用,本身也是分布式的&…...

数据库访问被拒怎么操作?
就一点: !!!!!! cmd打开命令窗口直接输入 mysql -u root -p 然后加密码打开数据库服务再去试试!! !!!!&…...

Vue 2 生命周期即将结束
本文章翻译自 Vue 2 is Approaching End Of Life 文章原作者 youyuxi 2024 年即将到来,我们想借此机会提醒 Vue 社区,Vue 2 将于 2023 年 12 月 31 日达到生命周期结束 (EOL) Vue 2.0 于 2016 年发布,已有 7 年多的时间。这是 Vue 成为主流框…...
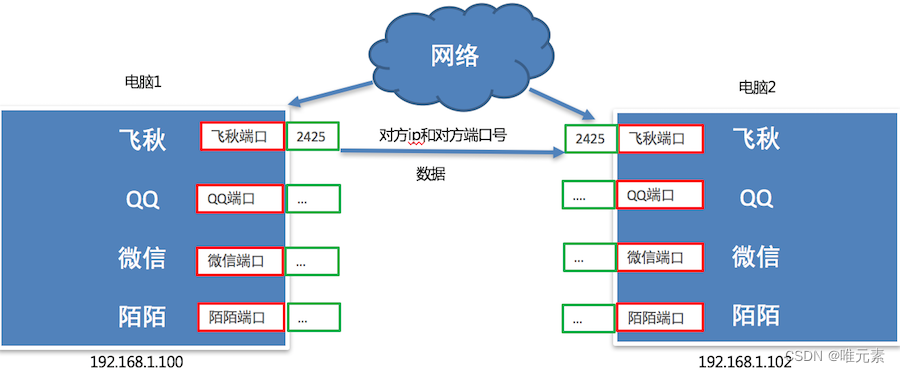
Python---端口和端口号的介绍
1. 问题思考 不同电脑上的飞秋之间进行数据通信,它是如何保证把数据给飞秋而不是给其它软件呢? 其实,每运行一个网络程序都会有一个端口,想要给对应的程序发送数据,找到对应的端口即可。 端口效果图: 2. 什么是端口 端口是传…...

Electron训练笔记
终端乱码解决办法:更改编号下载卡住解决办法:Electron RequestError: connect ETIMEDOUT 20.205.243.166:443electron本质是一个依赖库,改依赖库提供了部分对象,可以实现对于window的调用。electron有一个主进程,多个渲…...

2023 英特尔On技术创新大会直播 | 窥探未来科技的边界
2023 英特尔On技术创新大会直播 | 窥探未来科技的边界 写在最前面观后感其他有趣的专题课程 写在最前面 嘿,你是不是对科技和创新充满好奇?2023 英特尔 On 技术创新大会线上活动邀请你一起探索最前沿的科技世界! 这不仅是一场普通的聚会&…...

机器学习之逻辑回归,一文掌握逻辑回归算法知识文集
🏆作者简介,普修罗双战士,一直追求不断学习和成长,在技术的道路上持续探索和实践。 🏆多年互联网行业从业经验,历任核心研发工程师,项目技术负责人。 🎉欢迎 👍点赞✍评论…...

H-ui前端框架 —— layer.js
layer.js是由前端大牛贤心编写的web弹窗插件。 laye.js是个轻量级的网页弹出层组件..支持类型丰富的弹出层类型,如消息框、页面层、iframe层等,具有较好的兼容性和灵活性。 layer.js用法 1.引入layer.js文件。在HTML页面的头部引用layer.is文件&#x…...

「Verilog学习笔记」游戏机计费程序
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 timescale 1ns/1nsmodule game_count(input rst_n, //异位复位信号,低电平有效input clk, //时钟信号input [9:0]money,input set,input boost,output reg[9:0…...
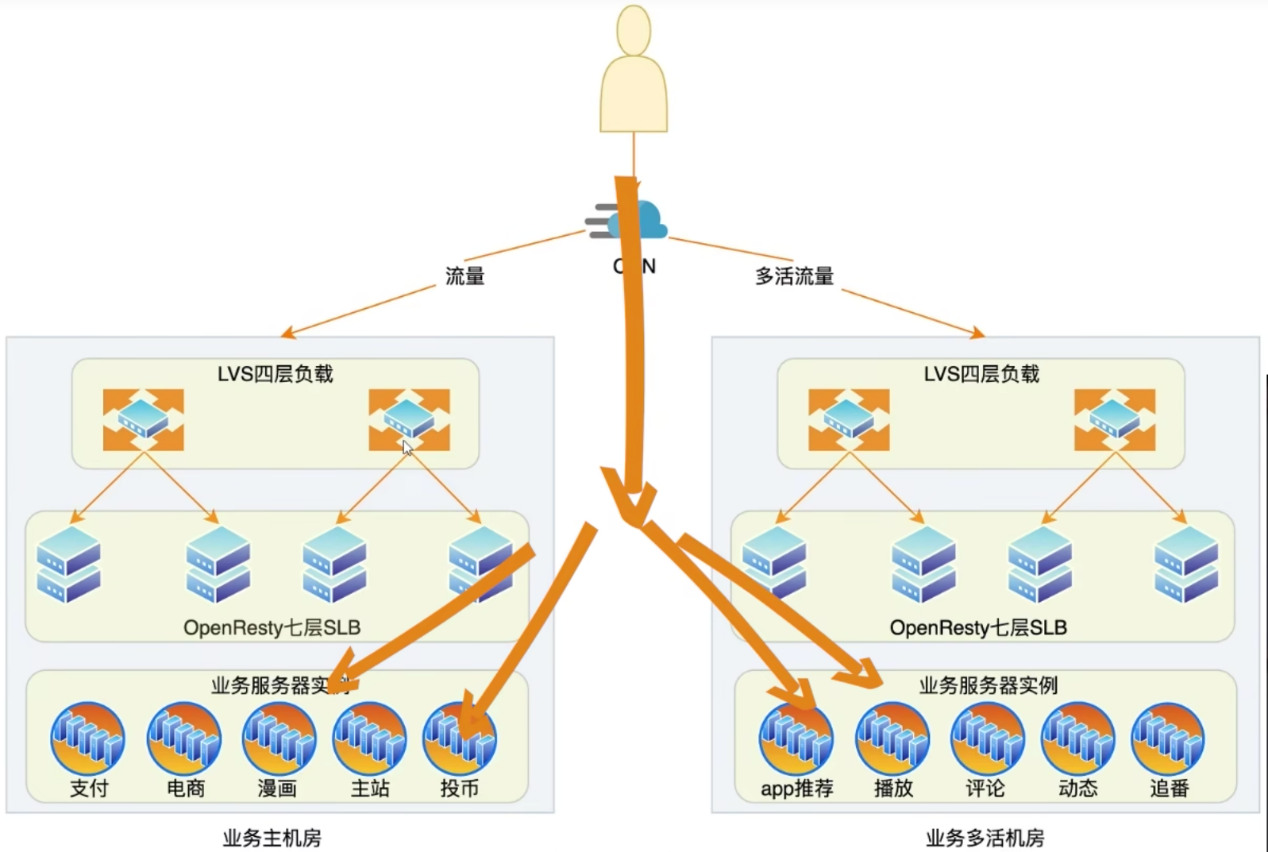
b站高可用架构 笔记
b站高可用架构 关键点:主机房,多活和多活机房 参考文章:bilibili技术总监毛剑:B站高可用架构实践 1. 前端和数据中心负载均衡 前端负载均衡(动态CDN):最近节点、带宽策略、可用服务容量 数据中心负载均衡:均衡流量、识别异常节…...
Android: Ubuntu下交叉环境编译常用调试工具demo for lspci命令(ARM设备)
lspci命令交叉环境编译(ARM设备) 交叉编译工具下载: https://releases.linaro.org/components/toolchain/binaries https://releases.linaro.org/components/toolchain/binaries/6.3-2017.05/aarch64-linux-gnu/ lspci命令交叉环境编译(ARM设备): 1&a…...

《2023全球IPv6支持度白皮书》近日发布
近日,全球IPv6论坛联合中国的下一代互联网国家工程中心面向全球发布《2023全球IPv6支持度白皮书》。白皮书显示,在过去一年,全球IPv6支持度大幅提升,部署应用成效显著。全球IPv6部署率超过40%的国家数量同比增长了30%,…...
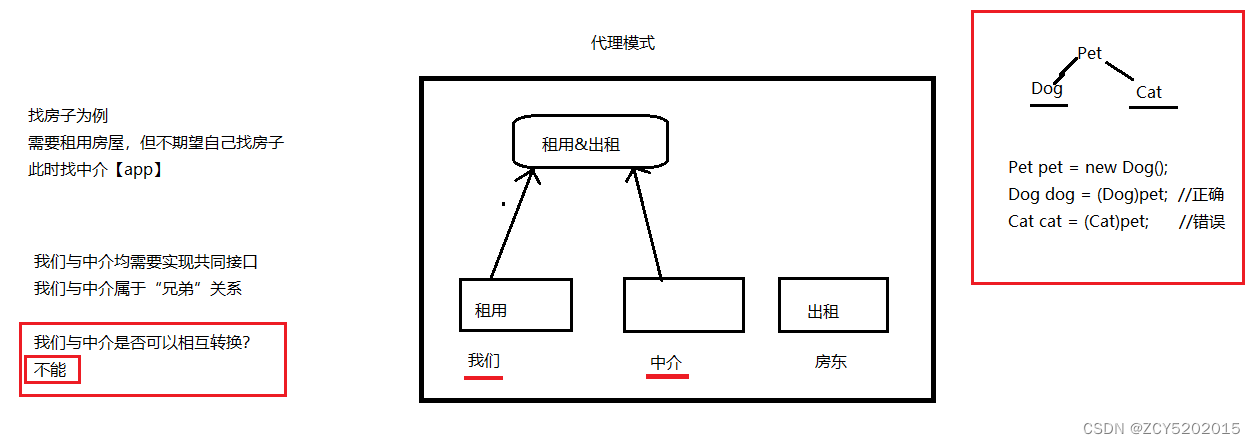
IDEA版SSM入门到实战(Maven+MyBatis+Spring+SpringMVC) -Spring的AOP前奏
第一章 AOP前奏 1.1 代理模式 代理模式:我们需要做一件事情,又不期望自己亲力亲为,此时,可以找一个代理【中介】 我们【目标对象】与中介【代理对象】不能相互转换,因为是“兄弟”关系 1.2 为什么需要代理【程序中…...

2023年度佳作:AIGC、AGI、GhatGPT 与人工智能大模型的创新与前景展望
🎬 鸽芷咕:个人主页 🔥 个人专栏:《linux深造日志》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! ⛳️ 写在前面参与规则 ✅参与方式:关注博主、点赞、收藏、评论,任意评论(每人最多评论…...

直播电商“去网红化”势在必行,AI数字人打造品牌专属IP
近年来,网红直播带货“翻车”事件频发,给品牌商带来了信任危机和负面口碑的困扰,严重损害了企业的声誉。这证明强大的个人IP,对于吸引粉丝和流量确实能起到巨大的好处,堪称“金牌销售”,但太过强势的个人IP属性也会给企业带来一定风险&#x…...
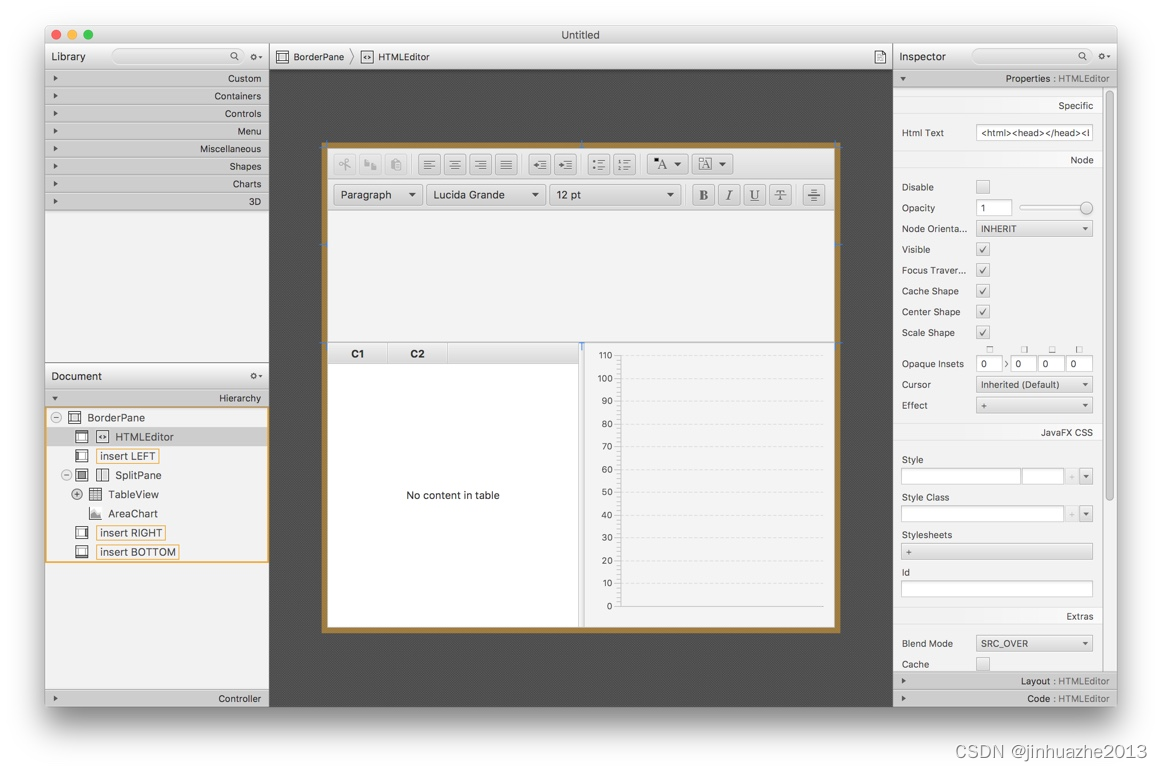
Java如何开发PC客户端(Windows,Mac,Linux)
项目编译工具:Gradle开发工具: Idea开发语言: 建议java17以上ui组件:openjfx (org.openjfx.javafxplugin)打包工具: jpackage (org.beryx.jlink) 一、如何解决打包问题 java 14以后,有了jpackage工具,能够…...

热红外图像非均匀校正方法
热红外图像中的非均匀性通常指的是热像仪在感知温度时出现的空间上的灵敏度不均匀。这种非均匀性可能是由于热像仪本身的制造差异、温度梯度引起的热漂移、光学系统中的不均匀性等因素引起的。为了获得更准确、可靠的温度信息,需要进行非均匀校正。 原因࿱…...

性能压力测试--确保企业数字化业务稳健运行
随着企业的数字化转型和依赖云计算的普及,软件系统的性能已经成为企业成功运营的关键因素之一。性能压力测试作为确保系统在各种条件下都能高效运行的关键步骤,对企业的重要性不可忽视。以下是性能压力测试对企业的几个重要方面的影响和作用:…...

【Java】7种逻辑运算,你了解几种
嗨,朋友们!今天我们聊点轻松的,来看看Java中那些常用的逻辑运算。可能你在学习编程的路上已经遇到过它们,但是让我们像闲聊一样,再重新认识一下这些小伙伴们! 那个老实巴交的“与”(AND&#x…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
